聯想問題本原,讓解題思路更為自然
——由一道模考題的講評說開去
江蘇 張朋舉
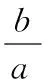
這是2017年南京市高三第二次模擬考試填空題的第14題,本題考的就是常見的恒成立問題,但由于學生沒能根據已知條件,將要求問題化歸為已解決的本原問題,導致沒能生成問題的解決策略,學生的得分率很不理想.筆者所教班級,全班42人,僅有12人做對了答案.而且,后期在對答對的12位學生進行訪談時,發現他們雖然做對了答案,但帶有很多偶然的因素,根本沒有把握問題的本原.
本原思想是相對學生而言的最樸素、最本質的想法.從問題的本原考慮就是以認清問題的本原為基礎,探尋解決問題的基本方法與規律,達到善于解題的目標,進而提升學生的數學素養.為了更好地發揮本題的功效,筆者借助本題的評講過程,試著讓學生回歸到本原問題考慮,自然生成解題思路,形成良好的解題思維習慣,實現高效解題.
一、評講過程
環節1:基于目標,探尋本原
師:上述是什么問題?有沒有做過這類或者相似的問題?
生1:恒成立問題,做過類似的題,比如:若不等式ax>lnx對任意x∈(0,+∞)恒成立,求實數a的取值范圍等.
師:分析到位,符合上述模考題的特點,下面我們從生1提供的問題出發,看能否有助于模擬題解法的探尋,解決生1的這個問題有哪些方法?
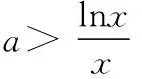
師:思路清晰!還有不同的想法嗎?
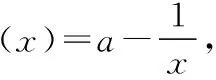
師:漂亮!還有不同的想法嗎?
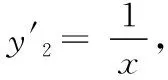
師:非常棒,三位同學從不同角度,用了不同的方法解決了生1提供的問題,哪位同學能給大家對比、分析下這幾種方法嗎?
生4:生1,2均是從“數”的角度考慮問題,其中生1是利用分離變量法處理的,一般情況下,在處理恒成立問題時,優先采用分離變量法;生2從已知條件結構入手,使用構造新函數F(x)=f(x)-g(x),轉化為求F(x)的最值問題,思路較為順暢;生3從“形”的角度解決問題,構造兩個函數的圖象,數形結合研究兩函數圖象的位置關系,值得學習.
設計意圖:以熟悉的問題作為本原,驅動課堂教學的進行,將本原問題融入到揭示、探究數學本質的活動過程中,實現一題多解,多解歸一,形成一類本原問題的基本方法.
環節2:把握目標,聯想本原
師:同學們,根據歸納出的多種解決策略,能否將方法遷移過來解決前面的模考題?
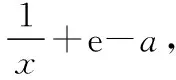
師:太棒了,當思路不“通暢”時,自然需要調整,向已經解決的本原模型靠攏,正可謂“山窮水盡疑無路,柳暗花明又一村”.
環節3:創新解法,源于本原
師:非常好!兩位同學將“本原問題”提供的解法,運用于新題之中,體現了方法的遷移,實現了“解一題,通一類”,然而巧妙的解法常常源于常規方法,抓住代數特點或幾何意義,運用巧妙方法,本題有創新的解法嗎?
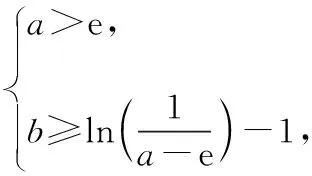

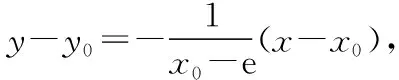
師:你們都太棒了!從本原問題出發,提煉方法,創新方法,然后用于新題之中,這才是真正的數學解題學習.回歸到問題本原考慮,奠定融會貫通的基礎,形成良好的思維習慣,實現了高效解題.
設計意圖:模考題經過包裝,將其本原隱藏起來,進而達到考查學生轉化問題和解決問題的能力;從問題的結論深入,發現其中與本原問題的聯系,在“形異神似”中實現方法的正向遷移.達到“解一題,通一類,帶一串,提一片”的目的.
環節4:試題命制,固化本原
師:通過本節課的學習,同學們認識了“一類問題”,通過聯想這類問題的方法,解決了原本不易解決得出的問題,這種將要求問題化歸為已解決的本原問題的思想,是同學們今后解題的一種重要思想方法.請同學們課下自主編制類似題,并嘗試這節課的解決思想方法.以下兩道題是課后經學生整理、自主編制的試題(成果展示).

【答案】(0,2].
命制題2:已知函數f(x)=(x+a)ex+b在原點處的切線垂直于x+y-3=0,若f(x) -msinx≥0對任意的x∈[0,π]恒成立,求m的取值范圍.
【答案】(-∞,1].
設計意圖:及時通過學生編制試題,固化本節思想方法,讓學生嘗到“把握本質問題”帶來的甜頭,通過課后搜集并編制類似題目,進而能更好地把握這類問題的本質,增強學習的自信心.
二、幾點思考
1.重視目標導向
目標導向解題,就是根據目標任務弄清要什么,理清有什么 ,然后縮小有什么和要什么之間的距離,進而嘗試怎樣縮小.解題過程也正是在問題的初始狀態和目標狀態之間進行比較、分析、消除差異,最終找到達到目的的最佳路徑的過程.這個過程中既要對條件多角度轉化,同時更離不開結論的目標導向.解題教學中,只有教師多關注、培養學生“讓結論引導思考”意識,那么當學生遇到復雜問題,就會主動根據目標導向,尋求解決問題的突破口,案例中,筆者根據目標導向,積極引導學生從目標入手,尋求解決問題的突破口,使問題的解決更為順暢,更有助培養學生思維的敏捷性和發散性.
2.聯想問題本原
讓學生養成將復雜問題退到最簡單、最原始問題的思維習慣是解題教學首要任務,這正如項武義教授所言“必須對基礎數學的本質和基本思想下一番深切的返璞歸真的功夫”.“本原思想”是指將一個數學問題的要素和基本結構作為思考的始點,是相對學生而言的最樸素、最本質的想法.解題教學應該積極引導學生探尋問題的本原,讓學生“跳一跳”就能夠到,應該抓住問題的本原,弄清問題的源與流,有意地將問題回歸為已解決的“本原問題”,自然生成解題思路.回歸本原問題,驅動解題教學,能夠充分發揮教師的主導作用.試題講評中,教師讓學生通過聯想已經解決的一道簡單問題,以簡單類似題作為本原問題,驅動解題思維,使解題思路自然生成.


