數學解題目標意識培養的重要途徑

甘肅 袁 琳

波利亞說：“學習數學就意味著學會解題”，如何將解題做到科學、規范、嚴謹，達到融會貫通、心領神會，是每個數學學習者的目標.

然而，筆者所屬貧困地區的數學教學不僅因有限的教學資源而制約，而且因學生的數學素養低、思維靈活性差而低效.從學生的解題實踐活動中，不難發現解題往往缺乏導向性、完備性、系統性.常會出現以下幾種解題偏軌現象：

1.注重了試題條件的任性分析，忽視了試題結論的目標導向.

2.注重了試題結論的目標探索，忽視了試題條件的受限剖析.

3.雖然既注重了試題的條件，又注重了試題的結論，但是在條件與結論間難以建構解題的通道口，在條件與條件間找不到連接點.

解題偏軌的根本原因在于學生解題的目標意識不強，目標思維欠缺，目標分解斷層.為了培養學生的解題目標意識，提高數學解題能力，在課堂的解題教學中，需加強解題的以下思維培養：

1.研判目標的原本性.要理解目標結論的內涵是什么？外延是什么？通過觀察、類比、猜想、轉化等思維過程，認清問題的結論所揭示的事實，理清問題的結論結構.

2.強化目標的導向性.要解(證)某一結論，需解(證)哪些中間結論，要解(證)中間結論，還需解(證)哪些結論，逐層推進，直至與已知對接.

3.提升解題的系統性.在一個縱橫交織的知識網絡、思維漩渦解題進程中，要整理出解答問題的層次結構，先后順序，就需將目標結論與題設條件放在同一平臺，剖析條件與結論間具有的內在因素，分析條件與條件間的串并關系，并有機地、有序地組合于一體，形成系統的解題思路.

如何將學生的解題目標意識培養落實到具體的教學中去，又有哪些有效的途徑呢？筆者曾做過一些問卷調查、實踐嘗試及深度反思.現將個人的一些見解整理如下，以供同仁指正.

一、借助反置思維，探尋解題的目標入口

反置思維就是把試題中的結論反置為條件，以結論為解題的抓手，并與題設的部分(或整體)條件有機結合，通過轉化、推演，得出一個題設條件的“結論”，或是不證自明的“結論”，這個“結論”便是解題的目標入口.

在解題中，常遇到此情形：面對一個題設條件過于單一或過于復雜的問題，由于條件與待解(證)的結論之間的“代溝”過大，難以形成思維的共鳴，無法架構思維的橋梁，從而使得問題解答找不到思路的基點，怎么辦呢？有一個行之有效的辦法——反置思維，或許能撥云見日，化解解題的疑難.

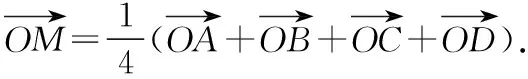
反置思維視角下的解題分析：該題所給的僅僅是一個問題的情景，顯性的約束條件少，思維的口子寬，從哪里下“刀”，切開這個“題糕”呢？這個第一“刀”是解題的難點，也是關鍵點.下面通過反置思維進行挖掘解決問題的目標入口.

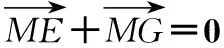
二、滲透數學思想方法，打開解題目標的通道

數學思想是數學的靈魂，數學方法是數學的軀體，數學思想與方法是解題的指導法寶.合理、準確地運用數學思想與方法來解題，有利于確立解題的方向，有利于高視角下分解與組合問題的主干結構，有利于優化思維結構，為解題的目標意識注入新的活力.

案例二：已知不等式ax2-2x+b>0的解集為(3,5)，則實數a,b的值分別為________.

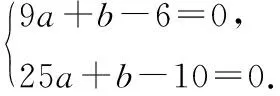
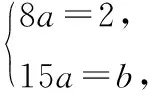
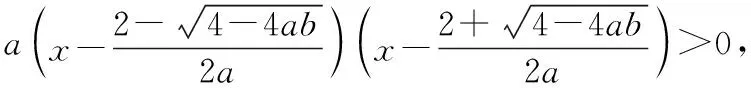
三、引入思維導圖，構建解題目標的系統

數學解題的思維導圖就是運用圖文并重的方法，把試題的各級知識點的關系，用相互隸屬與相關的層級圖表現出來，形成一個解題的思維的形象的系統.

初對一個題設條件相對多，結論相對抽象的問題，或許我們的解題是迷茫的，不知所措，是從哪個條件著手呢？要解(證)目標結論，得需解(證)哪些中間小目標結論呢？不妨引入數學思維導圖，從導圖中尋求解題的思維方向，建構解題的層級目標，形成解題的目標系統.繪制數學思維導圖，有利于培養學生的分析問題的能力，整合知識的能力，有利于提高學生思維的系統性、完備性，為數學解題的目標意識的培養奠定一個堅實的技術指導.

那么，如何繪制思維導圖呢？首先，將結論作為解題的根圈，然后剖析給定的每個條件，提示其具有的數學本質，并作為解題的葉圈.接著，內化條件，相互轉化，推出所需小目標結論，以連線方式結成枝干.最后，理清各個枝干的內外層級、因果關系、前后順序，有機地鑲嵌到根圈上，形成一個完整、完美、和諧的解題路線圖.

案例三：設函數f′(x)是奇函數f(x)(x∈R)的導函數，f(-1)=0，當x>0時，xf′(x)-f(x)<0，求使得f(x)>0成立的x的取值范圍.

思維導圖視角下的解題分析：在繪制思維導圖時，首先要明確以下幾個解題的重要小目標：

1.待解結論是抽象函數不等式的解集，這類問題的一般性解題的策略是什么？

此類問題的一般性解題策略為：利用函數的單調性脫去函數的符號“f”，化抽象不等式為具體不等式，并運用不等式的性質加以解答.顯然，一般性解題的策略給出了解題的總目標是做什么的，為解題指明了方向.

2.由條件“x>0,xf′(x)-f(x)<0”你能聯想到什么？它所揭示的問題的本質是什么？在實現總目標的過程中，能起到什么作用呢？

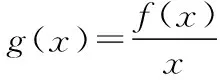
3.條件“函數f(x)(x∈R)是奇函數”從“形”的角度而言，函數的奇偶性刻畫了函數的什么特性？在實現總目標的過程中，又能起到什么作用呢？

函數的奇偶性刻畫了函數圖象的對稱美，偶函數的圖象關于y軸對稱，奇函數的圖象關于原點對稱.由2中的條件僅能研究(0,+∞)的函數圖象的變化趨勢，而(-∞,0)的函數圖象的變化趨勢，就根據奇函數的對稱性而得之.

4.條件“f(-1)=0”是用來干什么的？在實現總目標的過程中，又有什么作用呢？

在解題過程中，條件f(-1)=0的作用有二：其一，與條件“函數f(x)(x∈R)是奇函數”對接，可得f(1)=0；其二，由1可知：抽象函數不等式的解題的一般策略是利用函數的單調性脫去函數符號，在脫這個符號“f”時，需將待解目標 “f(x)>0”化為“f(x)>f(x0)”的形式，也就是說，條件“f(-1)=0”是用來替代f(x)>0中的0的.

5.不等式g(x)>0與f(x)>0的解集有何關系？

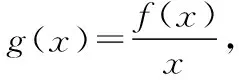
根據以上的解題的分析與思考，可繪制如下的思維導圖：

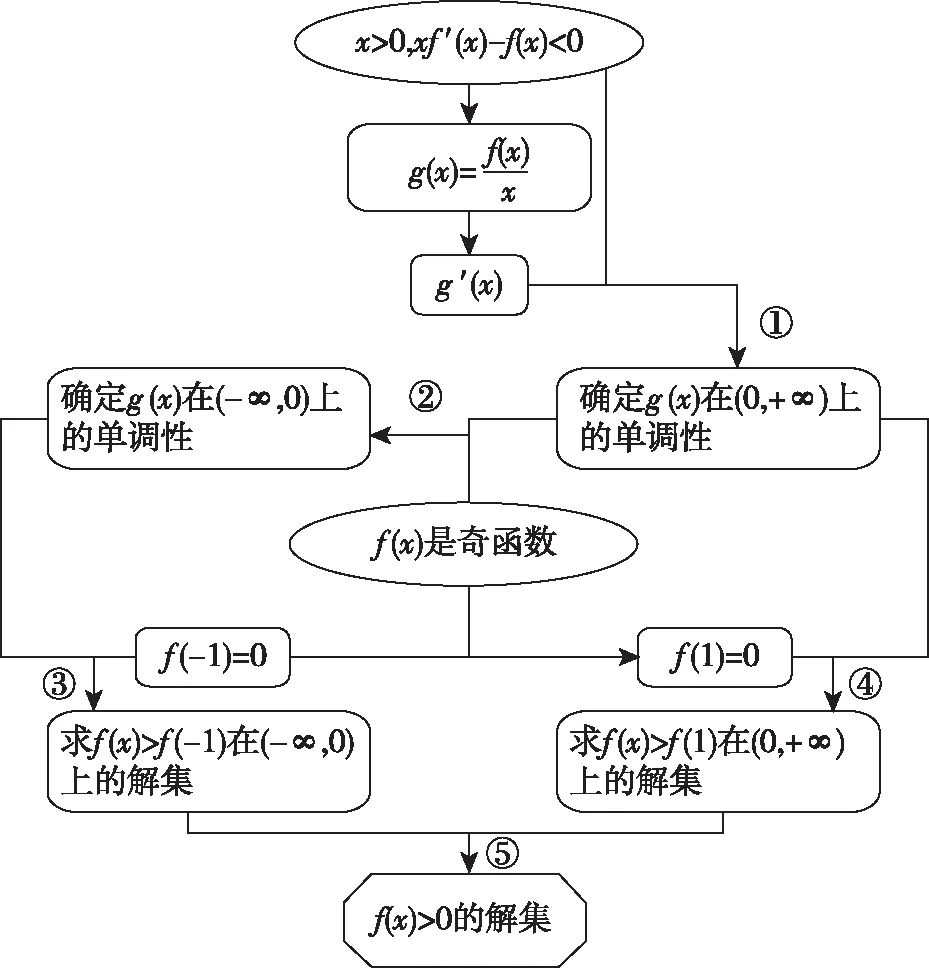
(本文是甘肅省教育科學“十三五”規劃“隴原名師”專項課題“數學解題目標意識培養”(課題立項號：GS[2017]MSZX034)研究成果)