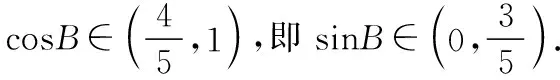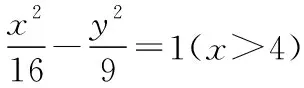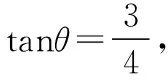軌跡思想在解三角形中的應用

安徽 胡 廣

解三角形是高中數學的重要內容，也是高考的重點考查對象.解三角形的主要方法是根據正余弦定理以及三角形中的邊角關系，然后利用相關三角函數公式等數學知識進行三角形中邊角及面積等元素的計算.有些三角形問題還能與函數、不等式等知識結合，另外有些三角形問題如果能從軌跡思想入手，還可以將三角形問題轉化為解析幾何的問題.下文結合具體例題談談筆者的一些體會.

一、與圓結合

類型1：與三角形的外接圓結合

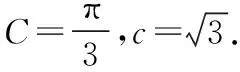
求 (1)△ABC面積的最大值；(2)a2+b2的最大值.

常規解法:(1)在△ABC中，由余弦定理，得c2=a2+b2-2abcosC. 即3=a2+b2-ab≥2ab-ab，得ab≤3.

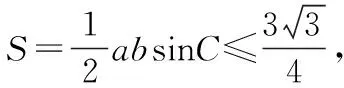
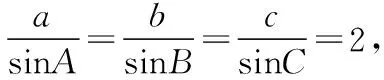
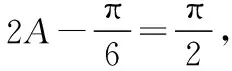
用軌跡方法求解：

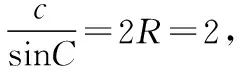
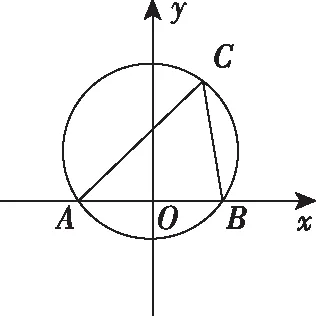
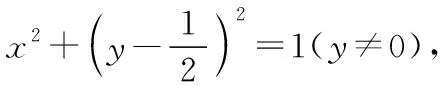
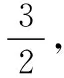
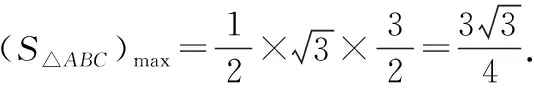
(2)設C(x,y)，則

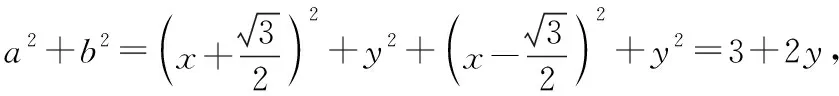
比較兩種解法可以發現，用軌跡思想處理相關的最值問題時，C點的位置對最值的影響比較直觀，所以解決起來比較方便.

類型2:與阿氏圓結合

(在平面上到兩定點距離之比為定值(定值不為1)的點的軌跡是圓)

示例2：在△ABC中，BD是∠B的平分線，且AD=1,CD=2，求△ABC面積的最大值.

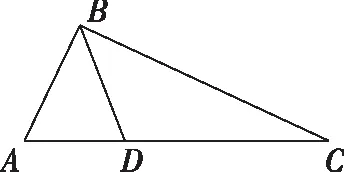
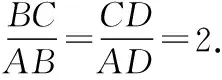
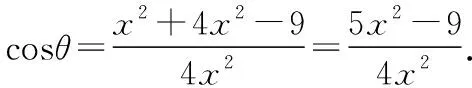
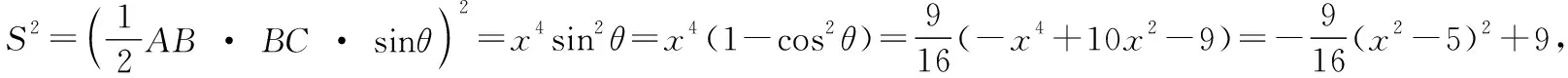
用軌跡方法求解：不妨設D為坐標原點，AC邊所在直線為x軸建立直角坐標系如下圖.則A(-1,0),C(2,0)

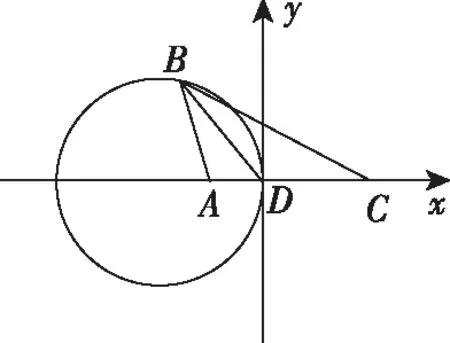
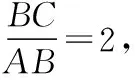
易知當B點位于(-2,±2)時，△ABC面積最大，此時S=3.

相對于常規解法而言，本題利用軌跡思想大大簡化了解題步驟，建立了三角問題與解析幾何之間的聯系.

類型3：與其他圓的結合

示例3：在△ABC中，AB=2,AC2+BC2=8，求△ABC面積的最大值.

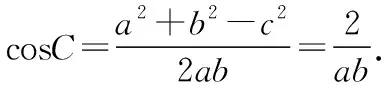
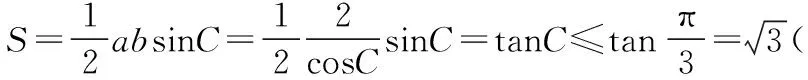
用軌跡方法求解：不妨以AB中點為原點，AB所在直線為x軸建立平面直角坐標系如下圖，則A(-1,0),B(1,0),令C(x,y),

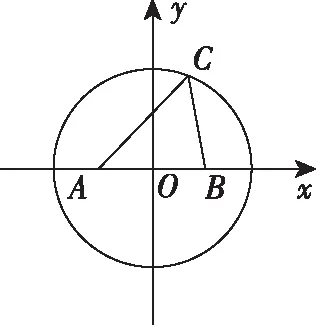
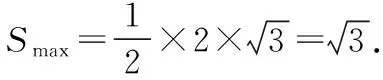
除了上述情形外，有些三角形問題還可以與圓錐曲線產生聯系.

二、與圓錐曲線結合

類型1：與橢圓結合

示例4:在△ABC中，角A,B,C對應的三邊分別是a,b,c.已知b=2,a+c=4,求中線BD的范圍.

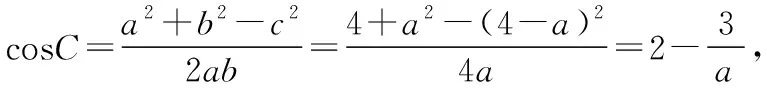
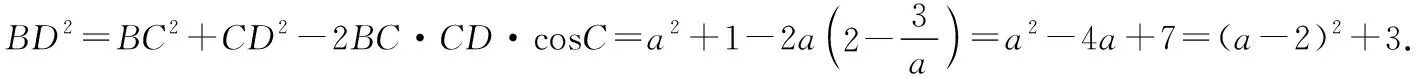
用軌跡方法求解：以D為坐標原點，AC邊所在直線為x軸建立直角坐標系如下圖，∵AB+BC=4,∴B點的軌跡是以A,C為焦點的橢圓(不包括長軸的兩個端點),

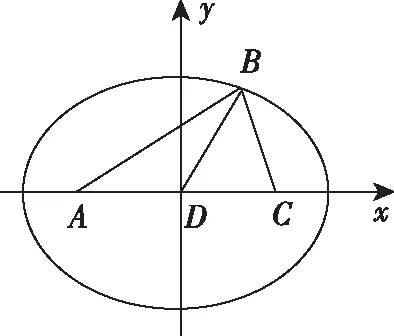
類型2：與雙曲線結合

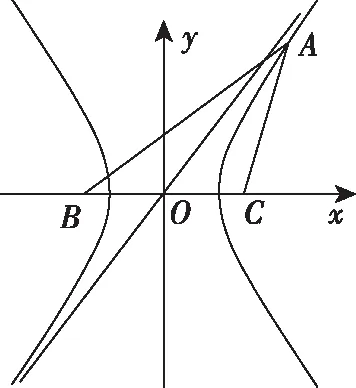
示例5：在△ABC中，角A,B,C對應的三邊分別是a,b,c.已知BC=10,AB-AC=8.求sinB的取值范圍.