多元最值問題的變式探究
■河南省潢川一中 王君昊
大家知道,基本不等式是高中數學的重要知識,高考對基本不等式的考查,主要以多元最值為背景的題型呈現,而多元最值問題的求解卻并非僅僅依賴于基本不等式。在高考中,多元最值問題形式多樣,綜合性極強,因而具有一定的挑戰性。面對變幻莫測的多元最值問題有何良策呢?讓我們從一道2018年的高考題說起。
【引例】(2018年天津高考)已知a,b∈R,且a-3b+6=0,則的最小值為。
解析:由a,b∈R,且a-3b+6=0得,3b=a+6。
評注:上述解法采用了代入消元法,從而把兩元最值問題轉化為一元最值問題,利用基本不等式求最值,這是求多元最值問題最基本的方法之一。
【變式1】(2018年江蘇高考)在△A B C中,角A,B,C所對的邊分別為a,b,c,∠A B C=120°,∠A B C的平分線交A C于點D,且B D=1,則4a+c的最小值為 。
解析:如圖1,因為∠A B C=120°,且B D為∠A B C的平分線,所以∠A B D=∠C B D=60°。
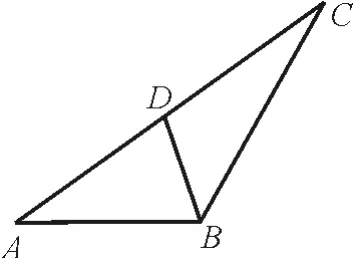
圖1
又因為角A,B,C所對的邊分別為a,b,c,且B D=1,所 以S△A B C=a csin 120°,S△B D C=asin60°,S△A B D=csin60°。
于是,由S△A B C=S△B D C+S△A B D得:a csin120°=asin60°+csin60°。
故a c=a+c,即
于是4a+c=(4a+c)+5=4+5=9。
評注:本題的難點在于從圖形中找出a與c的關系式:a c=a+c,即。本題解析中利用基本不等式求多元最值時采用了整體代換的數學思想。
【變式2】若x,y,z均為正實數,且x2+y2+z2=1,則的最小值為
解析:令1+z=t,則2>t>1。因為x2+y2=1-z2≥2x y,所以≥==,當且僅當t=1+z=,x=y時取等號。
評注:本題共有三個變量,解題的關鍵是利用基本不等式消元,解答過程中兩次應用了基本不等式,第一次應用基本不等式既起到了消元的作用,又起到了放縮的作用,第二次應用基本不等式是為了求出最值,在這里必須注意等號是否成立。
【變式3】已知正數x,y滿足2x y=,那么y的最大值為
解析:2x y==4x+。故y的最大值為。
評注:將兩個變量分離再將問題轉化為解對應不等式問題,體現了數學思想對數學解題的“統領”作用。
【變式4】若實數x,y滿足2x2+x yy2=1,則的最大值為
解析:把2x2+x y-y2=1變為(x+y)·(2x-y)=1。
令2x-y=t,x+y=。
。
評注:從本題解析中可以看出,引進參數不是增加變量,而是為了巧妙消元,引入一個變量t,消去兩個變量x與y,不僅使原式成為關于t的函數,而且可將其配成基本不等式應用的模式,真可謂“合理引參,巧奪天工”。

