數(shù)列中的創(chuàng)新題型
■浙江省諸暨市職業(yè)教育中心 王 凱
數(shù)列是函數(shù)概念的繼續(xù)和延伸,它不僅注重對同學(xué)們的運(yùn)算能力,分析問題和解決問題的能力的考查,更重視對同學(xué)們理性思維和創(chuàng)新意識的考查。數(shù)列中的創(chuàng)新題型都是以數(shù)列、不等式、函數(shù)、直線與曲線為載體,主要考查同學(xué)們觀察發(fā)現(xiàn)、類比轉(zhuǎn)化以及運(yùn)用數(shù)學(xué)知識分析和解決數(shù)學(xué)問題的能力。下面舉例談?wù)剶?shù)列創(chuàng)新題的基本類型及求解策略。
題型一 概念型創(chuàng)新題
例1在數(shù)列{an}中,如果存在非零常數(shù)T,使得am+T=am對于任意的非零自然數(shù)m均成立,那么就稱數(shù)列{an}為周期數(shù)列,其中T叫作數(shù)列{an}的周期。已知數(shù)列{bn}滿足bn+1=|bn-bn-1|(n≥2,n∈N),如果b1=1,b2=a(a≤1,a≠0),當(dāng)數(shù)列{bn}的周期最小時,該數(shù)列前2018項(xiàng)的和是( )。
A.670 B.671
C.1341 D.1346
解析:由已知bn+1=|bn-bn-1|(n≥2,n∈N),且b1=1,b2=a(a≤1,a≠0),故b3=|b2-b1|=|a-1|。根據(jù)周期數(shù)列的定義,當(dāng)T為2時,由|a-1|=1,得a=0(舍去)或a=2,但a=2不滿足bn+1=|bn-bn-1|(n≥2,n∈N);當(dāng)T為3時,由||a-1|-a|=1,得a=0(舍去)或a≥1,故a=1,最小周期為3,該數(shù)列為1,1,0,1,1,0,…,前2018項(xiàng)的和是2×672+2=1346,選D。
點(diǎn)評:這類題的特點(diǎn)是首先給出一個新定義,然后根據(jù)定義提出一系列問題。解題策略是:仔細(xì)閱讀題意并捕捉相關(guān)信息,緊扣定義,圍繞定義與條件,結(jié)合所學(xué)的數(shù)學(xué)知識和方法,通過歸納、探索、推理、計(jì)算,發(fā)現(xiàn)解題方法,然后解決問題。
【變式訓(xùn)練1】在一個數(shù)列中,若每一項(xiàng)與其后一項(xiàng)的積為同一個常數(shù)(有限數(shù)列的最后一項(xiàng)除外),則稱該數(shù)列為等積數(shù)列,其中的常數(shù)稱為公積。若數(shù)列{an}為等積數(shù)列,且a10=2,公積為6,則a1·a5·a9·…·a2017等于()。
A.2503B.2502C.3505D.3502
解析:由a10=2,且公積為6,得a9=3,進(jìn)而得到a1,a5,a9,…,a2017均等于3。總共有多少個3相乘?問題轉(zhuǎn)化為“已知首項(xiàng)為1,公差為4的等差數(shù)列,求2017是數(shù)列中的第幾項(xiàng)”,由于2017=1+504×4,所以2017是數(shù)列中的第505項(xiàng),,從而可得答案為C。
題型二 數(shù)列性質(zhì)創(chuàng)新題
例2已知數(shù)列{an}(n∈N*)滿足:an則
解析:由an=-an-3(n≥7且n∈N*),可得n≥7時,an+6=an,于是知a2018=a8=-a5=-5。
點(diǎn)評:本題主要通過對數(shù)列形式的挖掘得出數(shù)列特有的性質(zhì),特有的規(guī)律,從而達(dá)到解決問題的目的,其中性質(zhì)探求是解題的關(guān)鍵。
【變式訓(xùn)練2】若數(shù)列{an}(n∈N*)是等差數(shù)列,則數(shù)列,(n∈N*)也是等差數(shù)列。類比上述性質(zhì),相應(yīng)地:若數(shù)列{cn}(n∈N*)是等比數(shù)列,且cn>0,則有數(shù)列,(n∈N*)也是等比數(shù)列。
解析:由已知“等差數(shù)列前n項(xiàng)的算術(shù)平均值是等差數(shù)列”可類比聯(lián)想“等比數(shù)列前n項(xiàng)的幾何平均值也應(yīng)該是等比數(shù)列”,不難得到也是等比數(shù)列。
題型三 數(shù)列運(yùn)算創(chuàng)新題
例3定義一種“*”運(yùn)算:對于n∈N*,滿足以下運(yùn)算性質(zhì):(1)2*2=1;(2)(2n+2)*2=3(2n*2)。則用含n的代數(shù)式表示2n*2為
解析:這里2*2=1,相當(dāng)于告訴了數(shù)列的首項(xiàng)為1,而(2n+2)*2=3(2n*2)實(shí)際上是一種遞推關(guān)系,即,故2n*2可以看成是一個首項(xiàng)為1,公比為3的等比數(shù)列,則2n*2=3n-1。
點(diǎn)評:數(shù)列運(yùn)算的創(chuàng)新題有時很隱蔽,需要認(rèn)真捕捉相關(guān)信息,抓住問題的本質(zhì)。這類題有時也可以從特殊到一般,先分析前幾項(xiàng),找出規(guī)律,再探究。
解析:由等差數(shù)列前n項(xiàng)和公式的推導(dǎo)方法知:倒序相加,可得f(x)+f(1-x)=。所以f(-12)+f(-11)+f(-10)+…+f(0)+…+f(11)+f(12)+f(13)=。
題型四 情境創(chuàng)新題
例4如圖1,一個面積為1的三角形,現(xiàn)進(jìn)行如下操作:第一次操作,分別連接這個三角形三邊的中點(diǎn),構(gòu)成4個三角形,挖去中間一個三角形(如圖2中陰影部分所示),并在挖去的三角形上貼上數(shù)字標(biāo)簽“1”;第二次操作,連接剩余的3個三角形三邊的中點(diǎn),再挖去各自中間的三角形(如圖3中陰影部分所示),同時在挖去的3個三角形上都貼上數(shù)字標(biāo)簽“2”;第三次操作,連接剩余的各三角形三邊的中點(diǎn),再挖去各自中間的三角形,同時在挖去的三角形上都貼上數(shù)字標(biāo)簽“3”;……;如此下去,記第n次操作后剩余圖形的總面積為an。

圖1
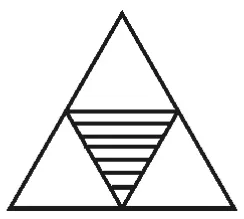
圖2

圖3
(1)求a1、a2。
(3)求第n次操作后,挖去的所有三角形上所貼標(biāo)簽上的數(shù)字和Sn。
解析:(1)
(2)因?yàn)閧an}是以為首項(xiàng),為公比的等比數(shù)列,所以
因?yàn)?1>40,32>41,33>42,34>43,35<44,所以當(dāng)n=5時,
因此,至少經(jīng)過5次操作,可使剩余圖形的總面積不足原三角形面積的。
(3)設(shè)第n次操作挖去bn個三角形,則{bn}是以1為首項(xiàng),3為公比的等比數(shù)列,即bn=3n-1。
因此,所有三角形上所貼標(biāo)簽上的數(shù)字的和為Sn=1×1+2×3+…+n×3n-1。
則3Sn=1×3+2×32+…+n×3n。
點(diǎn)評:本題給出的背景新穎別致,給出的圖形只是問題的一個載體,先從“形”入手得出一個遞推關(guān)系,再轉(zhuǎn)化為等比數(shù)列,或者通過順次迭代,以求出其通項(xiàng)。
【變式訓(xùn)練4】《九章算術(shù)》“竹九節(jié)”問題:現(xiàn)有一根9節(jié)的竹子,自上而下各節(jié)的容積成等差數(shù)列,上面4節(jié)的容積共3升,下面3節(jié)的容積共4升,則第5節(jié)的容積為升。
解析:設(shè)該數(shù)列{an}的首項(xiàng)為a1,公差為d,依題意得:
題型五 知識關(guān)聯(lián)型創(chuàng)新題
例5設(shè){an}是公差不為零的等差數(shù)列,Sn為其前n項(xiàng)和,滿足S7=7。
(1)求數(shù)列{an}的通項(xiàng)公式以及前n項(xiàng)和Sn;
(2)試求所有的正整數(shù)m,使得為數(shù)列{an}中的項(xiàng)。
解析:(1)設(shè)公差為d,則,由等差數(shù)列性質(zhì)可得-3d(a4+a3)=d(a4+a3)。因?yàn)閐≠0,所以a4+a3=0,即2a1+5d=0。又由S7=7得7a1+21d=7,解得a1=-5,d=2。所以數(shù)列{an}的通項(xiàng)公式為an=2n-7,前n項(xiàng)和Sn=n2-6n。
設(shè)2m-3=t,則,分析可知t為8的約數(shù)。
因?yàn)閠是奇數(shù),所以t的取值為±1。
當(dāng)t=1,m=2時,,而2×5-7=3是數(shù)列中的項(xiàng);
當(dāng)t=-1,m=2時,,數(shù)列中的最小項(xiàng)是-5,不符合。
所以滿足條件的正整數(shù)只有1個,m=2。
點(diǎn)評:數(shù)列與數(shù)論的交匯問題通常以探索性、存在性問題出現(xiàn),此類問題是數(shù)列中的難點(diǎn),其綜合性較強(qiáng),解答策略是充分利用數(shù)列的通項(xiàng)與項(xiàng)數(shù)所具有的特點(diǎn),再利用數(shù)論中的知識加以解決。
【變式訓(xùn)練5】已知等差數(shù)列{an}的首項(xiàng)為a,公差為b,等比數(shù)列{bn}的首項(xiàng)為b,公比為a,其中a,b都是大于1的正整數(shù),且a1<b1,b2<a3。
(1)求a的值;
(2)若對于任意的n∈N*,總存在m∈N*,使得am+3=bn成立,求b的值。
解析:(1)由已知條件得an=a+(n-1)·b,bn=b·an-1。由a1<b1,b2<a3,得a<b,a b<a+2b。
因a,b都為大于1的正整數(shù),故a≥2。
又b>a,故b≥3。
再由a b<a+2b,得(a-2)b<a。
由b>a,故(a-2)b<b,即(a-3)b<0。
由b≥3,故a-3<0,解得a<3。
于是2≤a<3,根據(jù)a∈N*,可得a=2。
(2)a=2,對于任意的n∈N*,總存在m∈N*,使得b(m-1)+5=,n∈N*,則b(2n-1-m+1)=5。
又b≥3,由數(shù)的整除性,得b是5的約數(shù),故2n-1-m+1=1,b=5。
所以b=5時,存在正自然數(shù)m=2n-1滿足題意。
總之,求解數(shù)列創(chuàng)新題的關(guān)鍵是仔細(xì)觀察,探求規(guī)律,注重轉(zhuǎn)化,合理設(shè)計(jì)解題方案,最后利用等差、等比數(shù)列有關(guān)知識來求解。在問題的求解過程中,需要我們不斷地觀察、感知、判斷、分析、綜合、推理,在推理中思考,在思考中尋找解題的模型,在模型的變換中形成解題的思維鏈條。

