基于集對分析與三角模糊數耦合的水質評價模型
王文川,李慶敏,徐冬梅,李文錦
(華北水利水電大學水利學院,河南 鄭州 450046)
隨著經濟發展,水生態問題越發引起關注,全面了解、把握流域水質污染驅動因子是水生態治理中的基礎性工作[1- 2]。從流域水污染驅動因子和水環境質量綜合評價,展開水質污染科學問題的探討研究,對構建符合我國河流特征的流域水生態治理體系,維護社會經濟持續發展和流域生態環境安全具有重要的意義[3]。目前,水質評價的方法有很多,如:主成分分析法[4]、單因子污染指數法[5]、綜合水質標識指數法[6]、模糊綜合評價法[7]、灰色聚類法[8]等。眾多學者從探討影響水質的主要驅動因子和對和流水質等別劃分等多個角度,進行水質評價方向的研究。如主成分分析通過將多個評價因子篩選出獨立、不相關的綜合因子,進而得到影響水質的主要驅動因子[9];模糊綜合評價基于模糊理論考慮評價水質過程中的水質模糊性、復雜性和綜合性,避免了不確定性的評價結果[10];單因子污染指數能較好的展現水質評價類別、功能區目標等信息。水質評價各有特點但在評價過程中也均有一定的局限性,如傳統的模糊綜合評價法利用最大隸屬度原則來確定水質類別,但當各水質評價指標所屬水質類別出現同步性較差時,往往難以建立有效的水質評價隸屬度原則,使評價結果易出現差異度小、均化和間斷等現象[11],傳統的綜合水質標識指數在指標權重分配上無法體現指標的差異性[12],集對分析可以較全面地描述水資源系統中的不確定性[13],該方法包容了模糊、灰色等不確定性判別方法的思想,通過用“同、異、反”三種狀態對研究對象進行描述,并用聯系數判別系統的歸屬程度。
水環境系統是一個典型的充滿不確定性的大系統,其水質往往受多種因素影響,具有較大的波動性。在進行水質測量時,單一測量值往往難以體現出水質測量結果應具有波動性的特征。三角模糊數則適用于數據資料較少或難以精確測量的情況,該方法被廣泛用于水質污染評價、水環境健康評價的研究中。本文將集對分析和三角模糊數結合,以區間的形式體現水質數據的波動性,利用三角模糊數和集對分析對竺山灣緩沖帶濕地的水質構建評價模型,為水質的評價理論方法提供新的思路。
1 評價方法
1.1 集對分析
集對分析理論(set pair analysis)是我國學者趙克勤先生于1989年提出的一種不確定性系統分析新方法[14],見圖1。
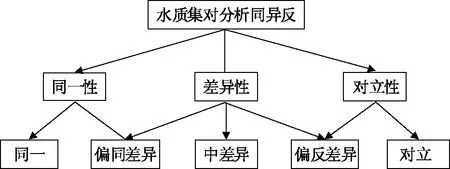
圖1 集對分析模型示意圖
集對是由一定聯系的兩個集合組成的基本單位,并用聯系數將其表達為:
μ=a+bi+cj
(1)
式中,a,b,c—分別為集對分析理論中的同一性、差異性和對立性,當a,b,c∈[0,1],且a+b+c=1;i—差異度系數,取值范圍:[-1,1];j—對立度系數,取值規定為-1。
由于在實際問題中,僅用三元聯系數無法對問題進行好的描述,故在此基礎上提出了多元聯系數,將對象描述為同一、偏同差異、中差異、偏反差異和對立,其表達式為:
μ=a+b1i1+b2i2+b3i3+cj
(2)
式中,a,b1,b2,b3,c—聯系分量,取值區間均為[0,1],且a+b1+b2+b3+c=1;i1,i2,i3—差異度系數;j—對立度系數。
本文所述的水質屬于越小越優型,展開上述聯系數表達式:
(3)
式中,m—第m個評價指標;n—第n個評價樣本;s—評價指標樣本值;s1~s5表示Ⅰ~Ⅴ級標準。
1.2 三角模糊數
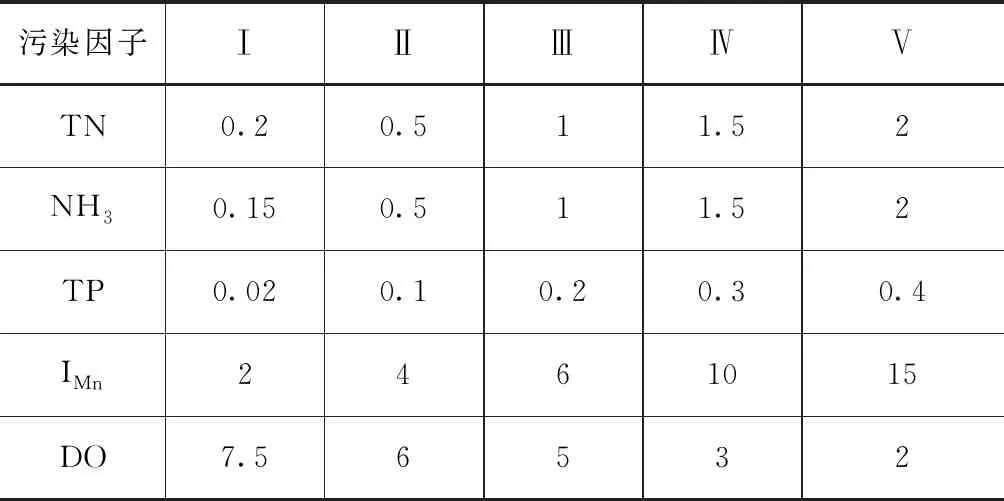
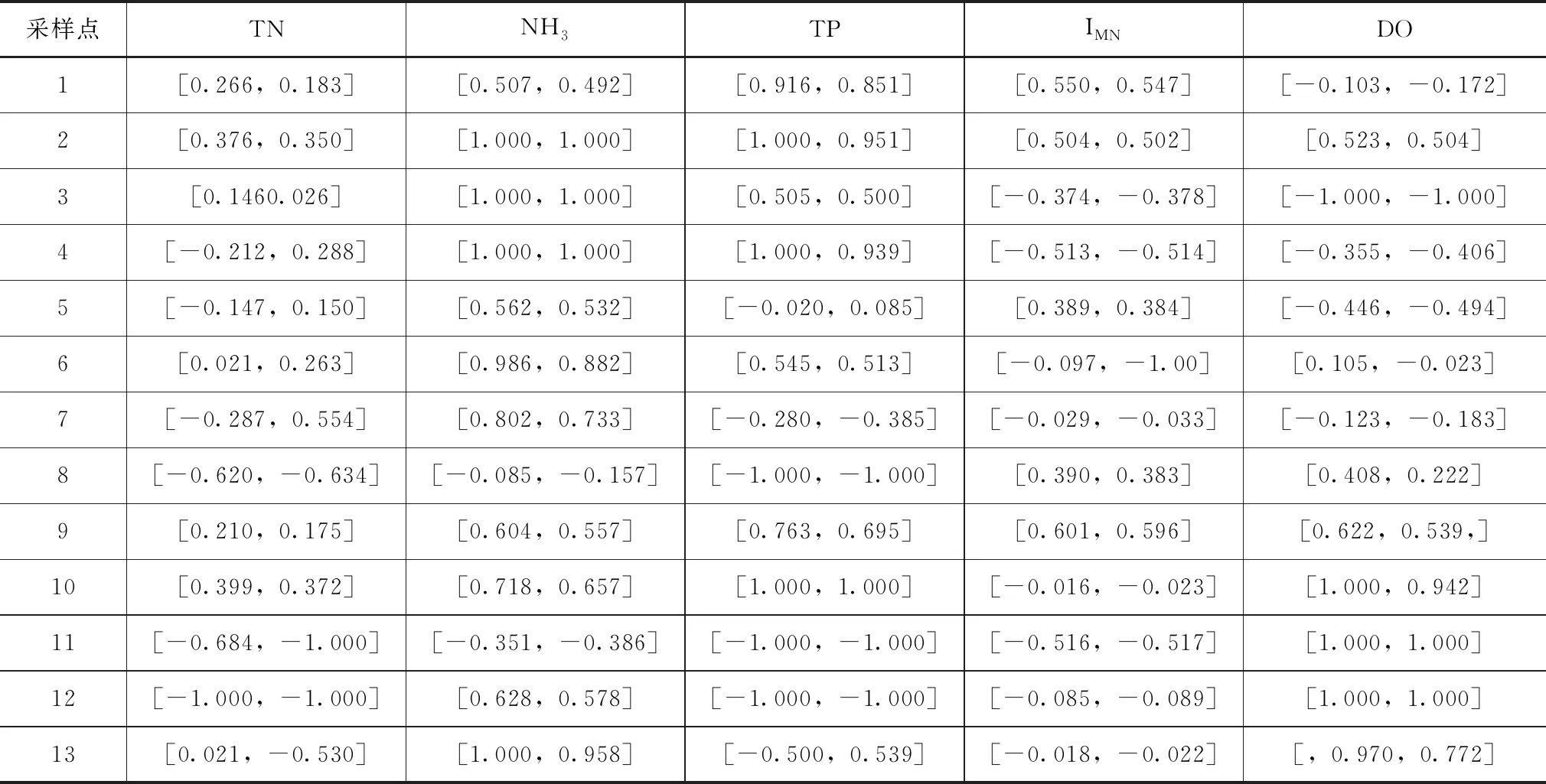
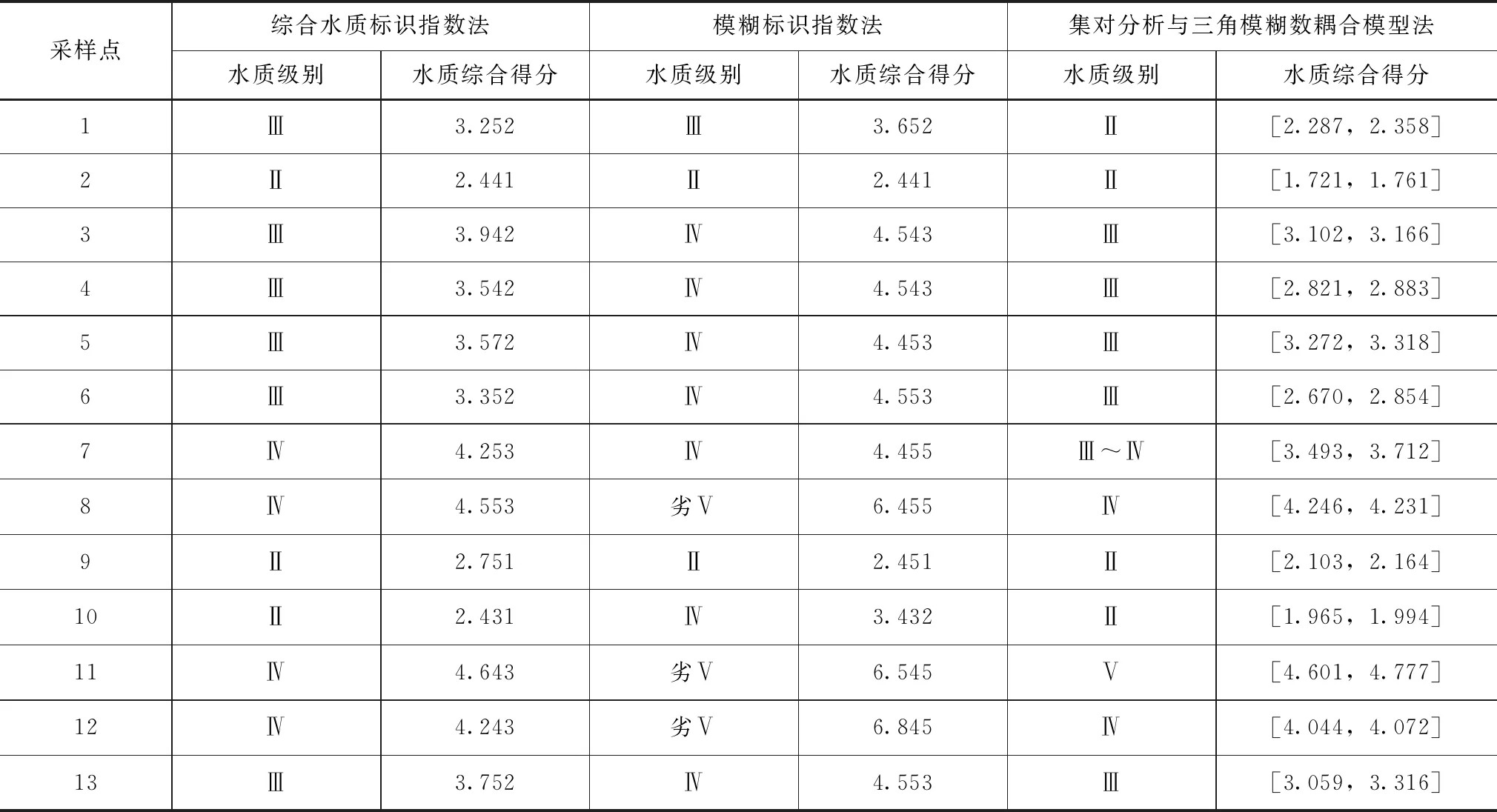
定義1[15]若a=(a1,a2,a3),其中,0 (4) 式中,μa—隸屬度;x—某一變量。 將三角模糊數利用α截集進行數據簡化處理。α為可信度,且α∈[0,1],數據區間由可信度水平決定,通常取α為0.9[16]。 (5) 集對分析式確定與不確定系統,其差異度的選取具有一定的模糊度,本文以三角模糊數(-0.5,0,0.5)為例,得到相應的差異度系數[17]。 (6) 式中,n取2,3,4,當s∈(s1,s3)時,η取2,當s∈(s3,s5)時,η取-2。 逐次計算求得矩陣數值的差異度系數后,結合設定的評價樣本指標權重,可求得相應樣本在設定置信區間內的綜合聯系數ym和等級值zm,計算公式如下[18]: (7) zm=3.5-2.5ym (8) 為驗證集對分析與三角模糊數耦合模型的可行性與有效性,以文獻[19]中的竺山灣水質實測數據為例進行計算。水質的評價與多項指標相關見表1,本研究將水質的分類選取溶氧量(DO)、高錳酸鹽指數(IMn)、總氮含量(TN)、氨-氮(NH3)、總磷(TP)五項作為評價因子,參考地表水環境質量標準(GB 3838—2002),可將水環境質量評價標準分為Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ共五類。 表1 地表水環境質量劃分標準限值單位:mg/L 對三角模糊數表示的水質區間數進行α截擊處理,處理結果參照文獻[19]。根據集對分析理論,構造水質評價聯系數矩陣。竺山灣水質評價方案有m個評價指標(m=5),n個評價樣本(n=13)。對 于區間形式,分別將和利用公式(6)算出差異度系數,差異度系數分為偏同差異度系數i1、中差異度系數i2、偏反差異度系數i3,將差異度系數代入公式(4),得出聯系數矩陣,計算結果見表2。 集對分析與三角模糊數耦合方法的權重選取文獻[19]中的權重,得到1×n的權重值矩陣w。 w=(0.1986 0.2046 0.2648 0.1980 0.1340) 表2 聯系數表示的竺山灣緩沖帶濕地水質數據 單位:mg/L 注:表中的數均是前面的大于后面的,這是由于公式6中需要加一個負號 表3 不同水質評價方法的竺山灣緩沖帶濕地水質評價結果 將表2中的聯系值結果和權重值矩陣根據公式(7)和(8)計算出相應的綜合聯系數和等級值。結果見表3。 根據集對分析與三角模糊數耦合模型計算的結果,對于采樣點7,結合原始數據,總氮(TN)處于Ⅳ類,總磷(TP)、高錳酸鹽(IMn)和溶氧量處于Ⅲ~Ⅳ類,結合目前對生態治理的重視,綜合評定為Ⅳ級更為合理;采樣點8、11、12三處污染嚴重,采樣點8、12評定結果均為Ⅳ類,采樣點11評定結果為Ⅴ類,這三處主要是由于總氮(TN)和總磷(TP)的含量過高導致;采樣點3、4、5、6、7、13六處污染較為嚴重,評定結果均為Ⅲ類,這六處主要是由于總氮(TN)、總磷(TP)及高錳酸鹽指數偏高導致的。總體分析,竺山灣水質處于污染狀態,這與文獻[16]和《太湖流域水資源公報2013》的結果基本一致。 從與綜合水質標識指數法及模糊標識指數法的對比發現,集對分析與三角模糊數耦合的結果與綜合水質標識指數法的評價結果較接近。 模糊標識指數法結合了改進的模糊層次分析法和綜合水質標識法的優點,不僅給出水質級別和水功能區達標程度,同時克服了不能評定劣Ⅴ類水質的缺點[20],但從評價的結果發現,采樣點8、11和12雖然總磷(TP)和總氮(TN)的含量偏高,但其余三個評價因子的含量處于Ⅱ~Ⅳ級,故該方法對于竺山灣濕地帶的評價結果偏高。 綜合水質標識指數法,該方法可以完整表達水體總體的綜合水質信息,結合定性、定量進行水質評價,對個別水質監測數據有較好的降噪性,能得出較為合理的水質評定結果[21]。結合原數據分析,發現評價結果合理,準確性較高。 本文方法利用集對分析,重視水質評價問題的不確定性,結合相應的權重強化了各監測點主要污染因子的作用,得出的結果相對可靠,但對于單個評價因子存在重度污染是,對綜合評價的影響結果不足,可能到能評價結果偏低,需要做出相應的改進。 竺山灣水質評定結果分布在Ⅱ~Ⅴ類,未能符合當地的水質要求,其中總氮、總磷、高錳酸鹽指數污染較為嚴重。因此,對于后期竺山灣水環境的治理應重點削減氮、磷、高錳酸鹽有機污染物。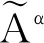
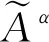
1.3 差異度系數
1.4 評價模型
2 實例應用
3 討論與結論

