分布式驅動電動汽車的近似最優轉矩矢量控制?

謝偉東，徐 威，付志軍，李 彬

(1.浙江工業大學機械工程學院，杭州 310014； 2.康考迪亞大學機械與工業工程系，加拿大蒙特利爾 H3G1M8)

前言

電動汽車具有清潔、高效和可持續等特點，是當今世界新能源汽車領域的研究熱點。其中，分布式驅動的電動汽車具有傳動高效和結構布置緊湊等優點，其驅動輪能獨立進行轉矩控制，使車輛的操縱性更加靈活，也為車輛穩定性控制提供了良好的前提。因此，開發分布式驅動的電動汽車穩定性控制策略不可或缺。

目前，車輛側向穩定性控制主要通過跟蹤穩態橫擺角速度來實現。文獻[1]～文獻[3]中通過后輪主動轉向進行穩定性控制。其中，文獻[1]中通過LQR的方法控制后輪主動轉向。文獻[2]中使用了非線性模型預測控制方法進行四輪轉向控制。文獻[3]中證明了四輪轉向搭配有效的穩定性控制策略能使車輛快速達到理想穩定狀態且避免車輛縱向性能的嚴重惡化。但LQR離線求解不能隨著外界環境的變化而自適應在線更新，魯棒性較差。此外，后輪轉向對車輛機械結構設計要求較高，且需要較為復雜的后輪轉向執行機構。文獻[4]和文獻[5]中利用橫擺角速度實際值和穩態值的誤差進行LQR反饋控制。文獻[5]中根據實際車速在不同的速度區間內使用插值法得到對應控制增益，一定程度上解決了LQR魯棒性差的問題，但控制增益的分段忽略了輪胎轉角的影響，且使用車輛線性模型，并未考慮輪胎實時的約束情況。文獻[6]～文獻[8]中則使用了轉矩矢量控制的方法，分別考慮了電機轉矩、輪胎滑移率和電池輸出功率等約束，進一步優化了控制策略的實用性，然而車輛縱向性能有所惡化。文獻[9]和文獻[10]中使用了車輛非線性模型，在轉矩矢量分配的基礎上進一步考慮輪胎力的約束，在仿真中取得了較好的控制效果。

本文中針對輪胎非線性的特性，搭建了輪胎側偏剛度變化的非線性車輛模型。同時，借鑒近似LQR的最優控制思想[11]，針對車輛非線性的特性，開發了基于車輛側向加速度實時調節橫擺力矩控制增益的方法。此外，考慮電機峰值轉矩和輪胎最大摩擦圓的約束，對驅動輪控制轉矩進行矢量分配，從而使車輛橫擺角速度得到有效的控制。通過圖形化編程軟件LabVIEW和多體動力學仿真軟件CarSim進行駕駛員在環聯合仿真[12]，驗證控制策略的有效性。最后，使用HIL系統驗證控制策略在實時系統中的可靠性。

1 系統建模

本文中以自主設計制造的雙電機后驅方程式賽車為研究對象。該車輛采用分布式驅動設計，每個后輪均由一個電機獨立驅動。具體車輛參數參見表1。

1.1 輪胎模型

為實現車輛的有效控制，須實時獲取輪胎縱向力和橫向力。當輪胎側偏角較小時，可認為輪胎側偏剛度為常數。然而，當輪胎側偏角逐漸增大時，輪胎工作在非線性區域，導致簡單的線性輪胎模型無法準確估算輪胎力。因此，為獲得較為精確的輪胎縱向力和側向力，本文中使用了魔術公式(MagicFormula)輪胎模型[13]。這是一種基于輪胎實驗數據和理論特性的半經驗模型，也是目前公認的最為準確的輪胎模型，其表述為

表1 車輛參數表

y＝Dsin(Carctan(Bx-E(Bx-arctan(Bx))))(1)式中:x為輸入變量，表示輪胎的垂直載荷、滑移率和側偏角；y為輸出量，表示對應輪胎的縱向力、側向力和回正力矩。模型中的參數B，C，D和E通過Matlab擬合由FSAE輪胎測試聯盟提供的輪胎實驗數據獲得。同時，為簡化輪胎力計算，默認輪胎外傾角為 0°。

為保證精確獲得輪胎縱向力和側向力，須對車輛各輪胎垂直載荷、滑移率和側偏角等參數進行實時在線估計。忽略車輛行駛過程中受到的空氣阻力，輪胎垂直載荷通過質心三軸加速度計進行估算，該方法也是目前較為有效且最為簡便的觀測手段[14]。輪胎線速度、滑移率和側偏角等參數通過采集輪速傳感器、質心三軸加速度計和陀螺儀等數據計算獲得。

1.2 非線性車輛模型

傳統的線性2自由度車輛模型具有計算簡便、且能較為準確地反映汽車曲線運動特征等優點。但它只適用于車輛側向加速度較小的情況(一般側向加速度小于0.4g)。當車輛在高速轉向時，該線性模型難以精確表征車輛的各項運動特性。因此，本文中結合線性2自由度車輛模型的優勢，搭建了輪胎側偏剛度變化的非線性車輛模型[15]，如圖 1所示。

圖中:在輪胎坐標系中，前輪轉角為δ，各輪胎側偏角為α，線速度為v，縱向力為Fx，側向力為Fy；在車身坐標系中，質心速度為V，對應縱向速度和側向速度分別為Vx和Vy，質心縱向加速度為ax，側向加速度為ay，橫擺角速度為γ，側偏角為β。

圖1 非線性車輛模型

當車輛在高速運行時，前輪轉角通常較小，若此時進行穩定性控制，可假設前輪轉角約為0°，即δl≈δr≈0。因此，可得到如下所示的車輛運動方程。

側向運動方程:

橫擺運動方程:

式中Mz為橫擺控制力矩輸入。通過改變兩個驅動輪的縱向力差值，即分別控制后輪的電機輸出轉矩以改善車輛的側向穩定性能。

由于輪胎的非線性特性，在提高車輛模型精確度的同時簡化計算，對輪胎側偏剛度進行當前點線性化處理，如式(4)所示，即計算當前輪胎側向力與側偏角的比值。

再將側偏角和線性化的輪胎側偏剛度代入式(2)和式(3)中，質心側偏角和橫擺角速度作為被控量，可得非線性車輛系統狀態方程:

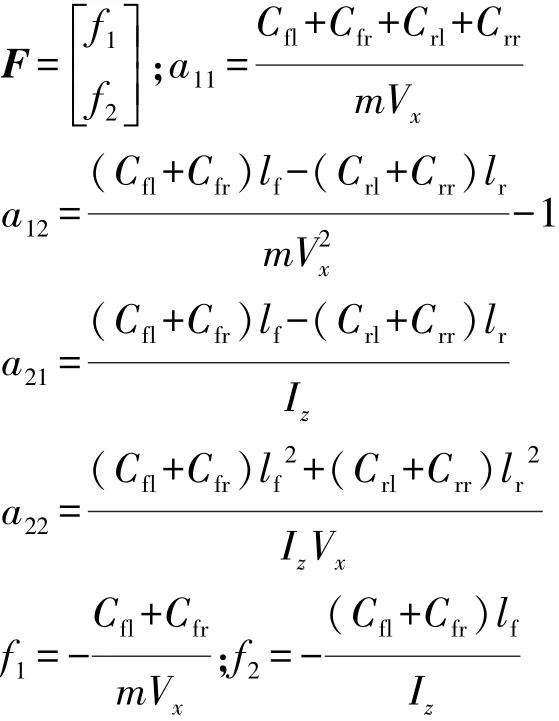
1.3 車輛參考模型

根據式(5)車輛狀態方程，當控制輸入Mz＝0時，可得質心側偏角和橫擺角速度與前輪轉角的傳遞函數表達式，將其簡化為1階傳遞函數[16]，由此得到車輛參考模型狀態方程:

而車輛質心的橫擺角速度穩態增益γ(0)為

其中:Ku＝m/l2·(lf/(Crl+Crr)-lr/(Cfl+Cfr))

考慮輪胎達到地面附著極限時，輪胎側向力接近峰值，理想橫擺角速度須根據側向加速度臨界值進行修正[17]，得到理想橫擺角速度臨界值為

式中σ為影響因數，本文中取值0.85。

因為質心側偏角數值較小，可使β(0)≈0。則車輛穩定控制目標期望的側偏角和橫擺角速度分別為

2 控制策略設計

根據分層式控制思想，將控制策略分為預處理器、控制器和后處理器3部分，如圖2所示。其中，預處理器對三軸加速度計、輪速傳感器和陀螺儀等采集的數據進行預處理，獲得車輛的基本狀態參數。再通過魔術公式輪胎模型計算各輪胎縱向力、側向力和側偏剛度等參數，并將數據輸入控制器和后處理器。

圖2 整車控制框圖

為使車輛跟蹤理想橫擺角速度，控制器根據車輛當前的輪胎狀態和橫擺角速度誤差計算車輛的橫擺控制轉矩。

最后，考慮輪胎峰值附著力和電機的轉矩約束，由后處理器根據車輛質心側向加速度對橫擺控制轉矩進行矢量分配，分別產生驅動輪控制轉矩ΔTl和ΔTr來實現車輛側向穩定性。

2.1 控制器

由于輪胎側偏剛度時變的特性，當系統受到無法預測的外界干擾時，難以保證受控系統的穩定性，所以針對系統變參數特性設計最優跟蹤控制器，使跟蹤誤差e＝x-xd→0，同時使≈0，從而保持跟蹤性能穩定。

為保證性能指標函數最小，借鑒文獻[11]中的近似LQR的控制方法，將最優控制輸入u分為兩部分，即u＝ud+ue。其中，ud為穩態控制輸入，ue為性能指標最優化的系統跟蹤誤差控制輸入。ud設計如下:

式中Ke＞0，為反饋增益常數。

將式(6)車輛參考模型代入式(10)中，可得系統穩態控制輸入ud:

由上式可知，由于(A-Ad)xd-Fdδ數值較小，所以ud數值主要取決于跟蹤誤差e的大小。

再將控制輸入u代入式(5)系統狀態方程中，可得

其中:Bued＝Bue+Fδ

由式(12)可知，ud的設計抵消了Ax，Bu和x·d的影響，并使系統轉換為和跟蹤誤差相關的LQR問題。由此，設計無限時間的優化目標函數J:

式中:Q為狀態變量的權重矩陣；q為質心側偏角β的權重系數；1-q為橫擺角速度γ的權重系數；R為反饋控制的權重系數。當參數q越大，則控制器更偏向對質心側偏角的控制，反之，則更偏重對橫擺角速度的控制。系數R越大，反饋橫擺力矩受到的限制越大，反饋橫擺控制力矩趨于減小，反之，則趨于增大[15]。為權衡質心側偏角和橫擺角速度的控制，使控制有所偏重，參考文獻[18]中的考慮路面附著系數和質心側偏角大小的動態權重系數調節方法(簡稱“β-μ”法)計算權重系數 q。

然而，由于LQR為離線計算求解，無法適用于非線性車輛的在線調節。因此，設計基于車輛質心側向加速度的最優反饋控制增益可調的控制方法。

選取車輛常見工作狀態時的質心側向加速度范圍0.1g～1.6g，將該范圍以0.1g為分辨率分成16組，并離線求解Riccati方程得到各組的最優反饋控制增益Ki。在車輛行駛過程中，根據實時質心側向加速度值所在區間插值計算獲得實時反饋控制增益K，如式(14)所示，并得到系統橫擺控制力矩Mz。

其中:ue＝B-1(Bued-Fδ)；ued＝-K·e

2.2 后處理器

為保證橫擺控制力矩得到有效的分配，后處理器須考慮在當前車輛狀態下電機峰值轉矩和輪胎最大附著力的約束，然后進行有效的驅動輪轉矩矢量分配。

由電機的特性所決定，在低轉速區間，電機便能輸出峰值轉矩。然而隨著電機轉速升高，峰值轉矩將會顯著降低。因此，擬合電機輸出轉矩曲線，并通過車輛減速器和輪胎半徑的計算，可得到輪胎在當前轉速下由電機驅動產生的最大縱向力Fm，max。

當車輛工作在極端工況時，輪胎達到峰值附著極限，根據輪胎最大摩擦圓理論[19-20]，可簡化計算得到輪胎在當前垂直載荷Fz時，地面所能提供的最大縱向力 Fw，max:

通過比較 Fm，max和 Fw，max，選取兩者中的較小值作為當前輪胎實際能達到的最大縱向力Fj，max。之后，驅動輪轉矩矢量分配根據車輛質心的側向加速度，分以下3種情況考慮。后處理器轉矩矢量分配策略如圖3所示。

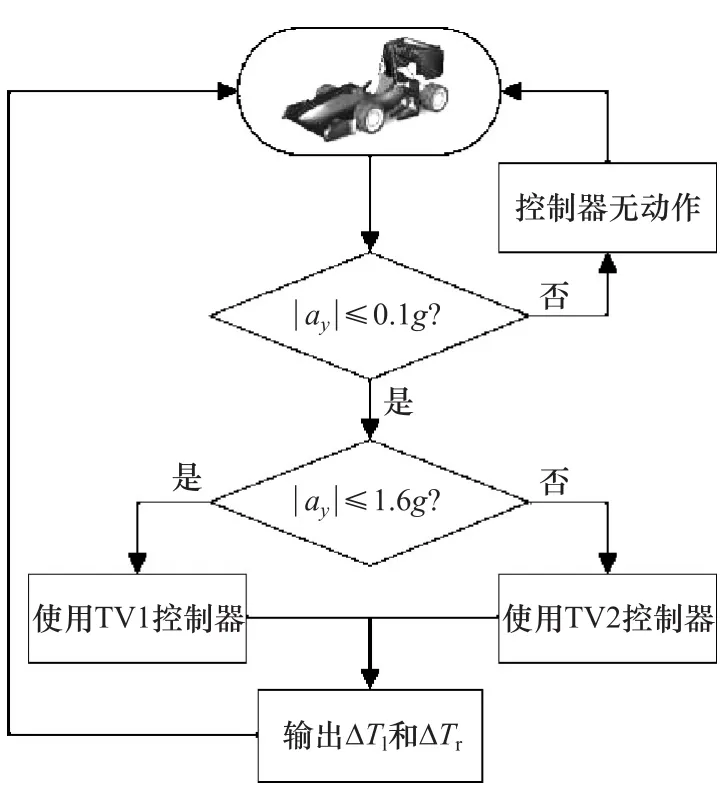
圖3 轉矩矢量分配控制策略流程圖

(1) ｜ay｜＜0.1g，控制器無動作。車輛在小角度轉向且低速行駛時，受到的側向力較小，此時進行側向穩定性控制意義較小。所以，為節約整車控制器運算內存，設定側向加速度下限值為0.1g，在此區間內，不啟動車輛穩定性控制程序，驅動輪輸出轉矩不發生改變。

(2) ｜ay｜＝0.1g～1.6g，啟用TV1 控制器。 車輛在常見的行駛工況時，質心側向加速度基本在此區間內。為不影響車輛的縱向性能，此時須保證兩個驅動輪的總輸出轉矩不變，所以矢量分配的左右驅動輪轉矩差值數值相等，即ΔTr＝-ΔTl。

(3) ｜ay｜＞1.6g，啟用TV2控制器。 當車輛質心側向加速度過大時，車輛的內側載荷過多轉移至外側，使內側輪的垂直載荷較小。根據魔術公式可知，垂直載荷的減小使輪胎附著力急劇減小，因而此時對內側車輪的驅動轉矩控制效果不明顯，所以TV2控制器使用了外側輪最大縱向驅動力控制策略。

3 控制策略仿真與實驗

3.1 聯合仿真

本文中研究車輛的整車控制單元為美國國家儀器公司(NI)生產的compact RIO嵌入式開發控制器，為節約控制策略的開發和測試時間，整車的控制程序均使用配套的編程軟件LabVIEW進行編譯。同時，聯合車輛動力學仿真軟件CarSim，以驗證控制系統的有效性。其中，CarSim中的所有車輛參數均來源于實際的車輛參數。

本次聯合仿真兩種不同的運行工況，第一種為轉向盤角階躍輸入，其次為8字繞環賽道工況。在每種仿真工況中，均對比了5種不同配置下的車輛運行狀態。第1種配置為理想狀態下車輛的動態響應或設定目標(理想)；第2種配置使用經典的LQR控制(線性控制)，即基于線性2自由度車輛模型離線計算的控制增益，因而只有一組增益且不能跟隨車輛狀態進行實時調節，并且產生的橫擺控制轉矩直接控制整車，故沒有進行轉矩矢量分配；第3種配置為使用本文提出的增益實時調節的控制方式(非線性控制)，但沒有使用轉矩矢量分配；第4種配置同樣使用本文提出的增益實時調節的控制方式，并且考慮輪胎和電機約束進行轉矩矢量分配(矢量控制)；第5種為車輛沒有任何穩定性控制(無控制)。

3.2 轉向盤角階躍輸入

在轉向盤角階躍輸入運行工況下，車輛以50km/h的速度勻速行駛，4s后轉向盤轉角輸入并在1s之內轉至30°。

圖4 階躍響應的橫擺角速度對比

圖4 為5種配置下的車輛橫擺角速度對比。由圖可知，非線性控制最接近理想值，而無控制時的車輛與理想狀態橫擺角速度差距最大。同時，使用經典的LQR控制能夠稍微改善車輛的側向性能，但控制效果遠不及非線性控制。此外，由于輪胎和電機的約束，雖然矢量控制的效果要稍遜色于非線性控制，但仍然明顯優于線性控制和無控制，并能較好地跟蹤理想橫擺角速度，穩態誤差僅約為2°/s。

圖5為在階躍輸入時車輛在矢量控制時的左右驅動輪的控制轉矩對比。由圖可知，質心側向加速度在當前工況運行中未達到1.6g閾值，因此左右驅動輪的修正轉矩數值相同，方向相反，從而保證整車的驅動力矩不變。此外，在4s左右時，車輛質心側向加速度達到0.1g時，即TV1控制器開始工作的瞬時產生了控制轉矩的峰值，但在之后的0.3s內迅速穩定，且在轉向盤轉角固定之后，控制轉矩也趨于恒定。

圖5 階躍響應的驅動輪控制轉矩對比

3.3 8字繞環賽道工況

8字繞環為大學生方程式汽車大賽的比賽項目之一，主要驗證車輛的側向穩定性能。具體賽道如圖6所示，內圓直徑均為15.25m，賽道寬3m，兩圓心相距18.25m。比賽時先繞右側賽道行駛2周，再切換至左側賽道行駛2周。根據比賽規則，要求能快速通過每一側賽道，也即更加關注單側的通過時間；另外也為節約仿真時間，故本次仿真僅測試左側單邊繞環情況，初始速度為12.5m/s。

圖6 8字繞環賽道圖

從圖7中5種配置的車速對比可知，當車輛開始轉彎時，縱向速度均有所下降，但矢量控制的車輛能夠較快地恢復行駛速度，且始終要快于其它任意狀態。然而，在非線性控制下，車輛的縱向速度受橫擺控制力矩的影響最大，為5種狀態中最低。線性控制對車輛縱向速度也有所影響，車速要稍微低于無控制狀態但要高于非線性控制。

圖7 8字繞環車速對比

圖8 所示為5種配置的車輛在8字繞環工況中的橫擺角速度對比。由圖可知，無控制時的車輛性能仍然為5種狀態中最差，與理想狀態偏差最大。此外，在前6s左右的時間內，矢量控制和非線性控制的效果最好，但在此之后，非線性控制下的車輛橫擺角速度急劇惡化。結合圖7分析可知，由于非線性控制的車輛在6s之后的縱向速度下降，導致車輛的側向性能也隨之下降。然而，得益于矢量控制，車輛的縱向速度變化幅度較小，因而始終能夠保持較好的車輛側向性能。而線性控制的車輛效果僅僅略微優于無控制狀態，但仍劣于矢量控制和非線性控制。

圖8 8字繞環橫擺角速度對比

圖9 為側向位移對比。由圖可知，在大部分時間內，非線性控制最接近路徑目標，即最貼近賽道內側且始終保持在賽道范圍之內，矢量控制次之，線性控制再次之，而無控制狀態的車輛偏離設定路徑最大。

圖9 8字繞環側向位移對比

圖10 為車輛在矢量控制時的驅動輪控制轉矩對比。由圖可知，車輛起始的側向加速度要小于1.6g，因此在TV1控制器工作下，兩側驅動輪控制轉矩數值相同，方向相反。但在約1s之后，車輛側向加速度達到閾值1.6g，TV2控制器開始工作，所以內側驅動輪即左后輪的控制轉矩為0，只有外側驅動輪產生控制轉矩。此外，外側輪的控制轉矩在控制器切換時產生輕微波動，但在大約0.3s之內控制趨于平穩。

圖10 8字繞環矢量控制時驅動輪控制轉矩對比

通過以上聯合仿真分析可知，即使非線性控制在所有配置中的縱向速度最低，但由于車輛的行駛路徑最短，完成時間仍短于線性控制和無控制狀態。此外，雖然矢量控制的車輛行駛路徑要稍長于非線性控制，但由于車輛的縱向驅動性能受橫擺控制轉矩的影響最小，車速要高于其它狀態，因而車輛通過賽道的時間最短，與非線性控制、線性控制和無控制狀態相比，通過賽道時間分別縮短0.073，0.280和0.348s。

3.4 硬件在環實驗

由于實車驗證控制系統的實時性具有較高的危險性，而硬件在環平臺能為控制系統的實時性提供良好的依據[21-23]，因此，搭建如圖11所示的硬件在環實驗平臺，以驗證控制系統實際應用的可靠性。

圖11 硬件在環實驗平臺實物圖

圖12 為硬件在環實驗的信號流程圖。通過上位機PC將整車控制程序寫入到cRIO控制器，并將CarSim車輛模型導入PXI中。在實驗過程中，PXI實時將車輛狀態參數發送至cRIO控制器并在上位機中同步顯示車輛動畫。cRIO控制器在接收到狀態參數之后，根據控制策略生成控制指令并傳輸至PXI和在上位機中顯示。

圖12 硬件在環實驗信號流程圖

本次HIL實驗運行工況為車輛在轉向盤角階躍輸入時的動態響應。為確保實驗的真實性，cRIO控制器按照車輛通信周期20ms進行控制指令的發送。實驗采用矢量控制，為分析驅動電機響應時間的影響，設定了無延時和5，10及20ms的電機響應延時[24-26]4種工況。

圖13為不同條件下的車輛橫擺角速度，圖14和圖15分別為在不同電機響應時間下的左右驅動輪控制轉矩對比圖。由圖13可知，當電機無響應延時且控制器同步發送控制指令，即聯合仿真時的車輛動態響應最好，轉矩控制最為精準且橫擺角速度的波動最小。此外，結合圖14和圖15分析，由于電機響應時間的影響，導致車輛的橫擺角速度在控制初始階段的偏差較大，因而左右驅動輪的控制轉矩出現短暫振蕩。而且，電機的延時越短，各驅動輪的轉矩控制越迅速，車輛也能更快地趨于穩定且使橫擺角速度波動更小。但是，所有狀態均能使得控制轉矩快速趨于平穩，車輛仍能快速趨于穩定，從而證明了本文中所設計的控制系統在實時環境中也能較好地改善車輛穩定性。

圖13 HIL實驗橫擺角速度對比

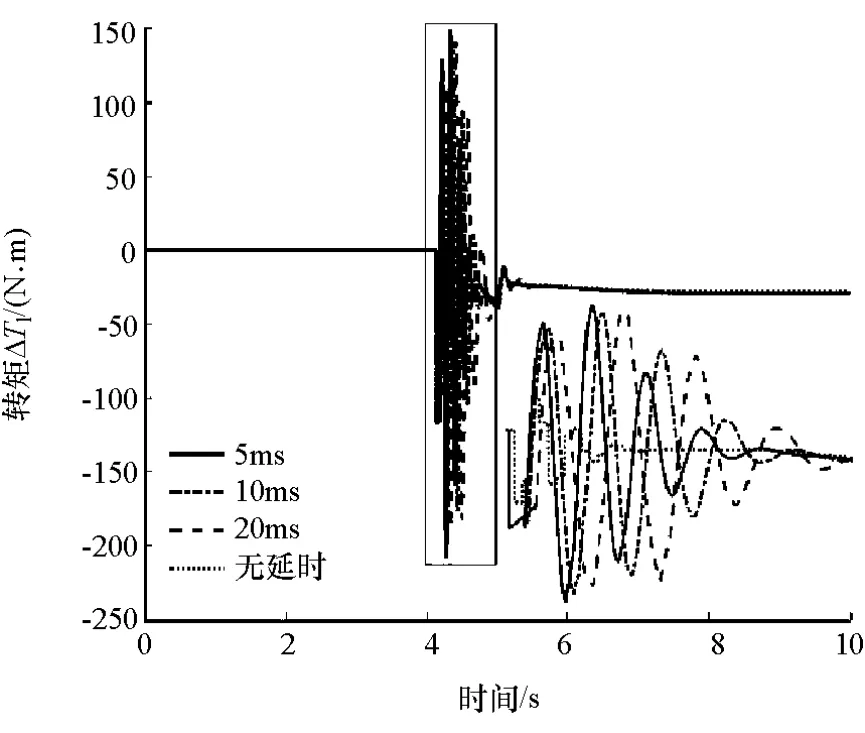
圖14 HIL實驗左側驅動輪控制轉矩對比

圖15 HIL實驗右側驅動輪控制轉矩對比

4 結論

本文中設計了一種增益可調的近似最優控制算法和帶約束的轉矩矢量分配控制策略。在控制器中，存儲著一系列指定質心側向加速度的離線橫擺控制增益，然后根據實際側向加速度所在區間范圍進行插值計算獲得實時的最優橫擺控制增益。此外，考慮驅動車輪轉矩受到電機峰值轉矩和輪胎峰值附著力的約束，對橫擺控制轉矩進行合理的矢量分配。最終，通過聯合仿真和HIL實驗，證明該控制策略能顯著改善目標車輛的側向穩定性，并使優化后的車輛能以更短的時間通過賽道。同時，驗證了控制策略在實時環境中仍具有良好的實時控制效果。