滾子分布方式對球面滾子軸承服役性能的影響

2018-12-12 13:21:04劉學婧劉磊徐華張勝倫邢宇

西安交通大學學報 2018年12期

劉學婧,劉磊,2,徐華,張勝倫,邢宇

(1.西安交通大學機械工程學院,710049,西安;2.浙江大學流體動力與機電系統國家重點實驗室,310027,杭州;3.西安工程大學機電工程學院,710048,西安)

由于風力發電設備承受的載荷較大,且受到實時風力、風速和風向變化的影響,會使得用于支撐以及傳動用的轉子系統出現撓曲現象。轉子撓曲會直接導致支撐軸承承受附加彎矩,進而降低軸承使用壽命,而運動副一旦損壞,輕則會引起機構振動加劇,重則直接造成機構損壞,而具有調心功能的軸承則能很好解決上述問題。

如圖1所示,雙列外球面滾子軸承(以下簡稱球面滾子軸承)主要由內圈、外圈、滾動體、保持架等幾部分組成。與其他類型滾動軸承最大的不同在于,憑借外圈內壁的球形結構以及橢球形的滾子,球面滾子軸承可以實現內圈相對于外圈在三維空間內自由旋轉,從而自動抵消由于轉子撓曲或軸承內外圈角度不對中所引起的附加彎矩,即自調心功能。由于內外圈之間沒有約束關系,所以球面滾子軸承不能承受彎矩。另外,球面滾子軸承的滾動體為滾子,且雙列布置,因而徑向承載能力極強;但軸向承載能力偏弱,僅用于承擔預緊力或是偶然的、小幅值的隨機載荷。球面滾子軸承一般體積、質量偏大,不易安裝和搬運,工作轉速較其他類型滾子軸承偏低。

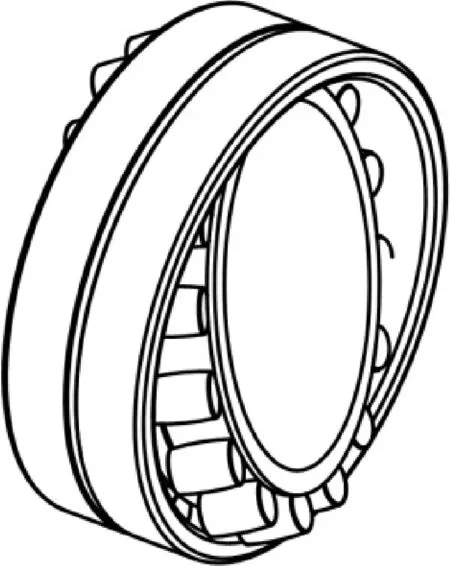
圖1 球面滾子軸承

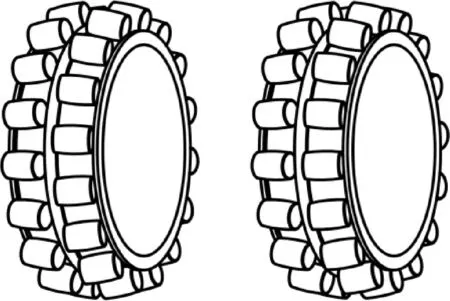
(a)交錯式 (b)平行式

對于球面滾子軸承而言,滾子分布方式有交錯分布和平行分布兩種,如圖2所示。現階段對于球面滾子軸承滾子分布方式的研究已經有了初步的進展。Bercea等建立了統一的雙列滾子軸承靜力學模型[1],不僅表征了不同類型的滾子分布方式,建模方法也適用于分析球面滾子軸承。在此基礎上,Sakaguchi等加入了離心力和陀螺力矩等因素,構成了典型的擬靜力學分析模型[2-3]。Yang和Ghalamchi等考慮了質量項和阻尼項,提出了基本的動力學方程[4-5],以此模擬不同滾子分布方式下的球面滾子軸承內圈動態特性。Ghalamchi等特別指出,對于徑向載荷而言,交錯分布的滾子更易降低內圈振動幅值。Cao等人建立的動力學模型[6-7],不但考慮了內圈的運動狀態(假設外圈固定),還考慮了滾子在法向上的振動,方程數從基本的3自由度擴展到3+N自由度,其中N代表每個滾子的法向移動自由度。Cao的模型僅考慮了交錯式滾子分布方式,因而得到的結論并不適用于兩列滾子相對獨立公轉的情況。An等在傳統的力學建模方法外,提出了一種故障診斷方法檢測球面滾子軸承的振動特性,并以此構建數學模型[8-9]。Xian對測出的振動信號分類,并進行回歸分析,擬合成球面滾子軸承的振動模型[10]。An和Xian是以特征信號來建模,導致模型并沒有重點關注軸承的幾何形狀,因此并未著重分析滾子分布方式對特征信號帶來的影響。

另有一些學者采用已經成熟的商業軟件進行球面滾子軸承的建模。文獻[11-13]分別利用Workbench建立了球面滾子軸承的模型,并完成了疲勞壽命、接觸應力及優化設計等方面的分析,認為交錯分布和平行分布在靜力學分析結果上并無本質區別,只是在受力位置和幅值上略有不同,這是由于滾子的位置角不同而造成的。馬方波等建立了能夠表征球面滾子軸承滾子分布方式的靜力學模型[14-15],也得出了類似的結論,交錯分布下單個滾子所受的最大載荷略小于平行分布下單個滾子所受最大載荷。張婁紅等對經典赫茲線接觸和Workbench的計算結果進行了對比,發現兩者的計算誤差較小[16],為球面滾子軸承的幾何結構設計、優化滾子分布方式等工作提供了理論支持。Fiedler等使用ADAMS建立球面滾子軸承的多體動力學模型[17],并研究了交錯分布式的滾子與滾道之間的接觸狀態與摩擦功耗。Houpert重點考慮了單個滾子與滾道的接觸狀態[18],并未指出滾道與多個滾子的聯合作用規律。

在實驗方面,Goodelle等觀測了滾子與滾道的接觸狀態與接觸區形貌[19],但靜態實驗結果難以獲得軸承的振動特性,也就無法獲得滾子分布方式對軸承實際服役性能的影響。Royston等測試出了球面滾子軸承徑向和軸向剛度及兩向的交叉剛度,重點介紹的是其提出的測試剛度阻尼的實驗方法[20]。趙景周通過對徑向游隙的測量,可以清楚地了解到不同形式分布的滾子在通過承載區時的跳動狀態具有明顯差異[21]。Desavale等僅測試了平行分布式球面滾子軸承的動態數據[22],因此無法獲知交錯式滾子分布對于軸承服役性能的影響規律。考慮到交錯式和平行式滾子分布方式會顯著影響軸承的服役性能,因此Houpert所獲得的經驗公式[23]對于平行式滾子分布的軸承來說并不適用。Maruschak等重點關注的是疲勞破壞的演化規律[24],而局部疲勞破壞與滾子分布方式并無直接關聯。

綜上所述,文獻大都認為兩列滾子交錯分布可以在通過承載區時滾子交替承擔外部載荷,因而服役平穩。平行式滾子方式因為相鄰滾子間的跨距略大,導致滾子以一個跨越的方式通過承載區,因而會出現較大的振動。但是,上述結論的前提是球面滾子軸承僅承受徑向載荷,而實際工況下,軸承往往會承受一定的軸向力,因此上述結論并不充分。此外,現有文獻大多忽略了調心工況這一特征,認為調心工況屬于故障工況,因此在模型中并未考慮調心作用的影響。再者轉子撓曲是由于外載荷過大而造成的,在實驗室的單一環境中難以提供足夠大的外載荷,因此如何設計具有自調心功能的實驗臺是需要研究的問題。

本文以適用于調心工況下的球面滾子軸承為研究對象,首先建立動力學模型,在考慮軸向外載荷、自調心功能的前提下,研究球面滾子軸承滾子分布方式對服役性能的影響,并設計具有自調心功能的實驗裝置驗證理論結果的正確性。

1 數學模型

1.1 單個滾子的受力分析

軸承的主要受力位置為滾子與內圈、外圈滾道之間的接觸區。假設接觸體在應力的作用下呈現小變形狀態,則該接觸區可視為是一個平面。為了便于計算,用矩形單元對該接觸區進行網格劃分。同時每個接觸區都有自身的局部坐標系,且各局部坐標系之間相互獨立:對于第i個滾子來說,接觸區內的xi和yi方向分別定義為平行和垂直滾子的滾動方向;而zi方向則垂直于xioiyi平面。根據赫茲接觸理論,在接觸區內任意單元的彈性變形等于柔度系數乘以力,而這個力是接觸區內對應單元應力的積分,變形表達式如下

(1)

式中:ω是某一單元的彈性變形;(x,y)、(x′,y′)表示該單元的坐標;ν為泊松比;E為彈性模量;S為接觸區的面積;p為某一單元的應力。

假設劃分的網格足夠細,那么每個網格的應力可視為恒定,此時式(1)可改寫為

(2)

式中:Fk為柔度系數,可表示為

(3)

其中,角標j、k代表接觸區中任意兩個單元,那么j單元的變形引起k單元產生的應力為

(4)

壓力等于網格面積乘以應力

Qk=4abpk

(5)

式中:a、b分別為矩形單元的長和寬。

彈性變形ωj亦可表示滾子與內圈、外圈滾道之間的彈性變形與兩者初始距離之間的差值

ωj=δi-κj

(6)

滾子與滾道之間的彈性變形δi可表示為

δi=D-D0

(7)

式中:D與D0分別表示受載前后滾子與滾道之間的距離

D0=Rw-Ri

(8)

其中Rw是滾道半徑,Ri表示第i個滾子的半徑。

Dx=D0cos(α0+αS)sinφi+δXsinφi

(9)

Dy=D0cos(α0+αS)cosφi+δycosφi

(10)

Dz=D0sin(α0+αS)+δz

(11)

式中:α0為初始接觸角;αS為自調心接觸角。考慮到每個滾子的位置不同,自調心接觸角可表示為

αi=αS(1-φi/90)

(12)

由于兩列滾子的分布方式不同,因此不同列滾子的位置角φi也不同,表達式如下

(13)

(14)

式中:φ0表示兩列滾子分布差異,當兩列滾子平行分布時,φ0=0,反之交錯分布時,φ0=π/Z;Z為單列滾子個數。

滾子與滾道間可看作兩個彈性體V1、V2相接觸,如圖3所示。兩者之間的初始距離可表示為

(15)

至此已經算出接觸區內任意單元所受的載荷,滾子與滾道之間的作用力即為同一接觸區內所有單元作用力之和

2009年入秋以來，我國云南、貴州、四川等西南地區發生了百年一遇的嚴重干旱，旱情持續時間之長、受災面積之大、影響范圍之廣引起了黨中央、國務院的高度重視。胡錦濤總書記對抗旱救災工作作出重要指示，溫家寶總理深入旱災最嚴重的地區指導抗旱救災工作，回良玉副總理等中央領導也多次作出重要指示，水利部部長陳雷強調要認真貫徹落實中央領導重要指示精神，把抗旱工作作為當前水利工作的重中之重，舉全部之力、全行業之力，全力以赴做好抗旱減災各項工作。

Qi=∑Qk

(16)

(a)赫茲接觸模型 (b)接觸區形貌

1.2 構建動力學方程

根據上述分析建立振動方程如下

(17)

式中:M為軸承質量;C為軸承阻尼系數;w為軸承列數;Z為單列滾子個數。

式(17)的第3項是用所有滾子的受力之和代替了位移與剛度的乘積。考慮到球面滾子軸承在服役時會受到x、y、z3個方向的外載荷,但不承受彎矩,因此將式(17)擴展如下

(18)

(19)

(20)

式(18)～(20)可用龍格庫塔法進行求解。

1.3 機構撓曲程度和自調心接觸角的估算

球面滾子軸承主要優勢在于能夠自動抵消由于轉子撓曲所帶來的附加彎矩,因此轉子的撓曲情況直接決定了球面滾子軸承自調心接觸角的方向和幅值。相比于其他文獻,本文根據已知工況條件對轉子的撓曲程度和球面滾子軸承自調心接觸角進行估算,而不是任意取值,可獲得更為準確的仿真結果。

對于單一變量的軸承剛度及多變量下的軸承剛度,如3自由度,可分別表示如下

(21)

(22)

圖4 轉子任意一個單元的位移及角位移自由度情況

轉子的剛度采用有限元法來獲得。將轉子分為若干個單元,假設每個單元有兩個節點,每個節點有兩個自由度,分別是徑向線位移自由度和角位移自由度,如圖4所示。根據有限元理論,獲得梁單元的剛度矩陣為

(23)

式中:Kr是轉子第i個單元的剛度矩陣;E是轉子的彈性模量;l是轉子第i個單元的長度;Ir表示轉子第i個單元的慣性矩,值為

(24)

式中:Dr為轉子截面的直徑。

在軸系中,軸承與轉子屬于并聯關系,共同支撐了外載荷。那么軸承-轉子系統的總剛度等于對應位置節點上軸承剛度與轉子剛度的線性疊加,即

(25)

式中:K為軸承-轉子系統總剛度矩陣;Kb為支撐軸承的剛度矩陣。

當獲得系統總剛度與外載荷后,即可獲得各節點位移,并可計算軸承及轉子所受的載荷,若滿足判定條件則計算結束。判定條件分為兩部分:一部分是每個軸承所受的載荷要等于轉子對應位置節點上的載荷;另一部分是以上兩部分的合力要與外載荷相等

(26)

若不滿足條件,則對軸承剛度進行修正。然后利用本次計算獲得的節點位移求出新一輪的軸承剛度,并與上一次的軸承計算剛度加權平均,得出新一輪計算所需的軸承剛度分量

kt+1=kt-1(1-λ)+kt

(27)

2 結果與討論

2.1 滾子分布方式對軸承振動的影響

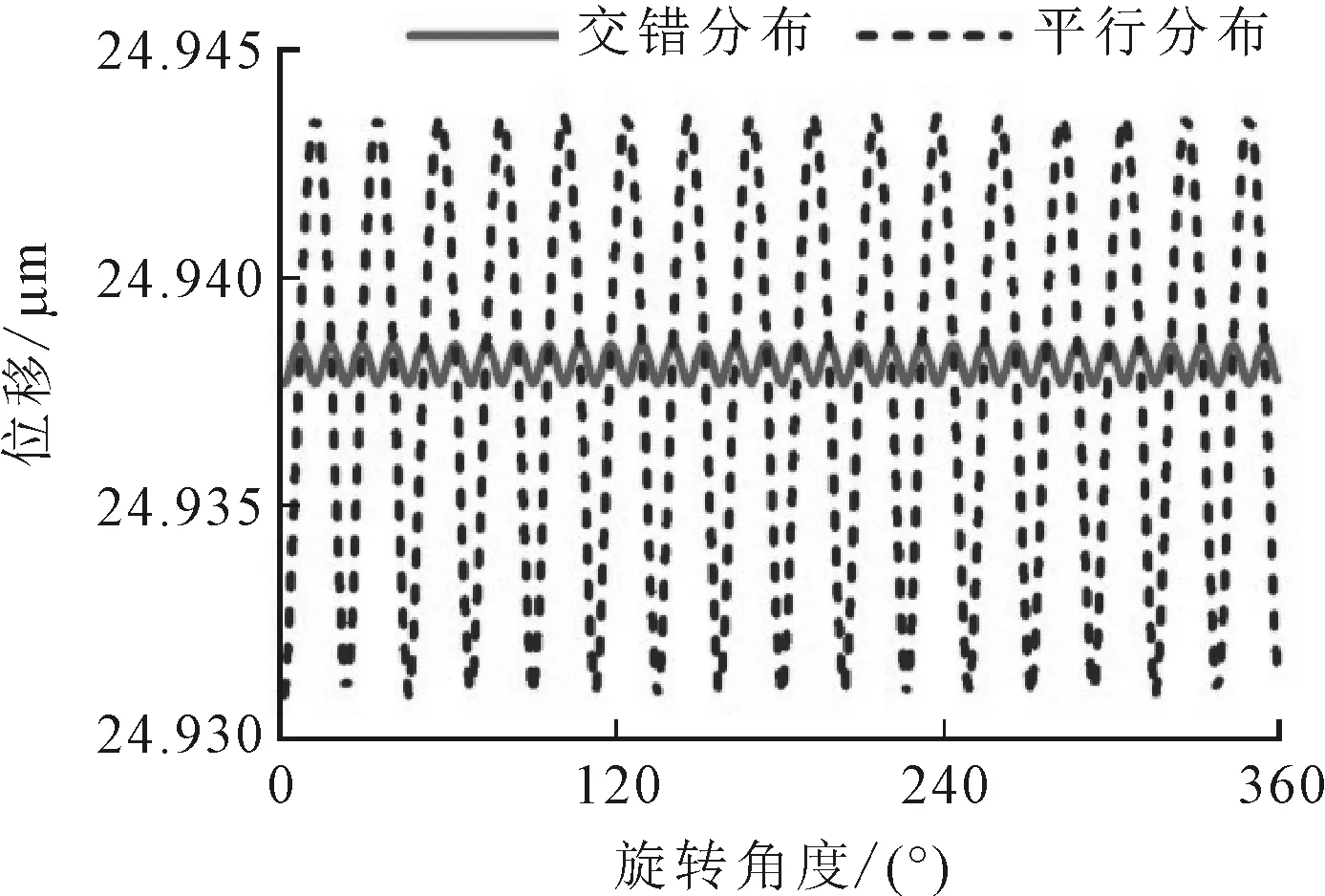
(a)無軸向載荷且初始接觸角為7.92°

(b)軸向載荷為500 N且初始接觸角為7.92°

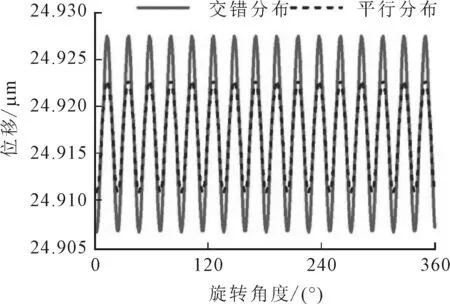
(c)軸向載荷為1 kN且初始接觸角為7.92°

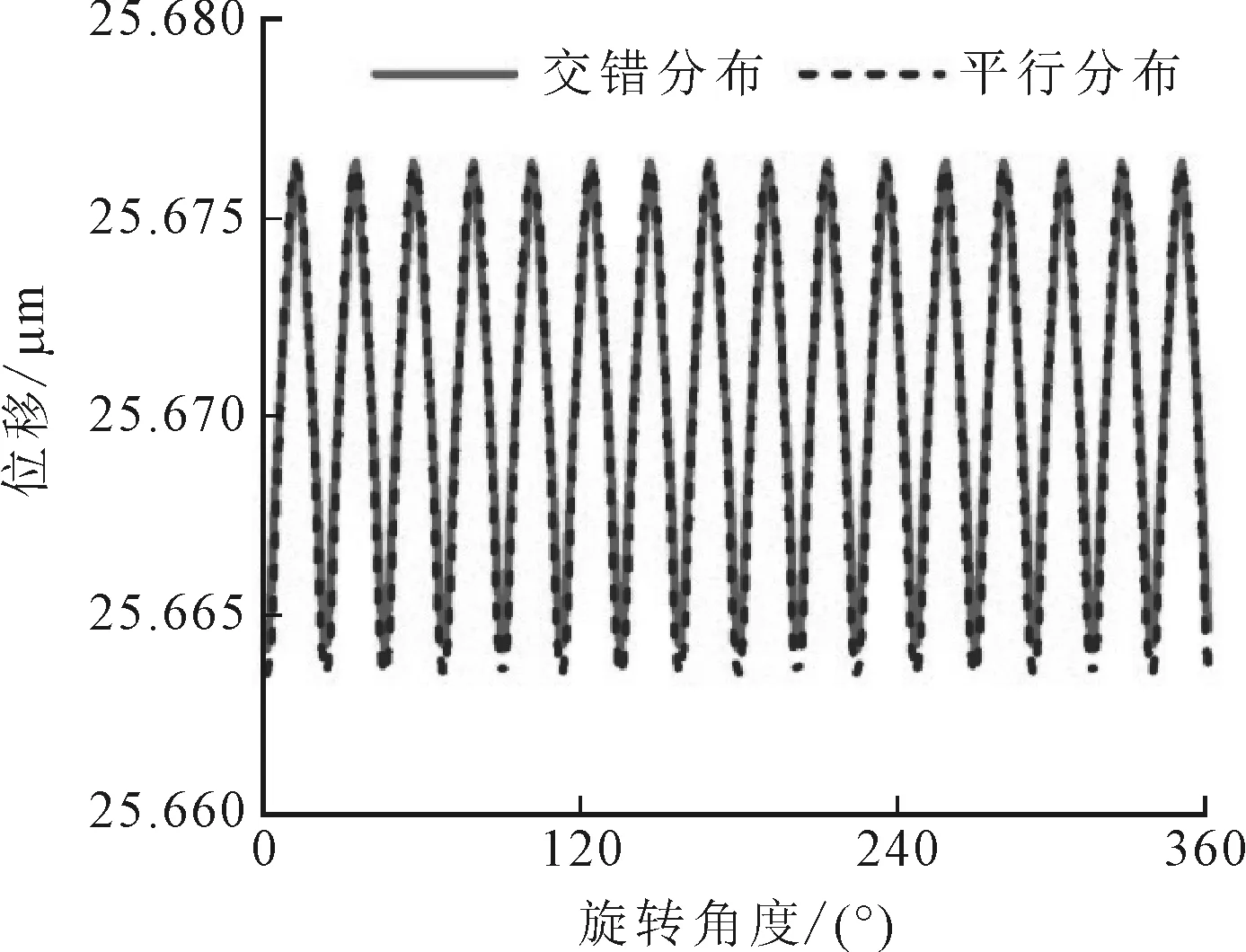
(d)軸向載荷為1 kN且初始接觸角為12.92°

球面滾子軸承一般有平行分布和交錯分布兩種方式,現有文獻大多認為,交錯式分布的滾子將更利于球面滾子軸承服役穩定性[5],如圖5a所示(仿真過程中徑向載荷設定為50 kN),但這一結論的前提是球面滾子軸承只承受徑向載荷。實際工況下,球面滾子軸承不可避免地會受到軸向載荷的沖擊。如圖5b所示,當徑向載荷幅值不變、軸向載荷為500 N時,交錯分布滾子所對應的軸承位移振蕩范圍明顯增大,而平行分布滾子所對應的軸承位移振蕩范圍沒有明顯的變化。當軸向載荷繼續增大至1 kN時,見圖5c,平行分布滾子的振蕩范圍要明顯小于交錯分布滾子的振蕩范圍。

平行分布的滾子在軸向上的剛度更大,因而可以更好地抵抗一定范圍內的軸向載荷沖擊。所以,對于以外部徑向載荷為主的工況,建議球面滾子軸承采用交錯式滾子分布方式;而對于有頻繁軸向沖擊的工況,建議軸承采用平行式滾子分布方式。另外,考慮到滾動軸承的軸向承載能力與初始接觸角成正比,所以適當增大初始接觸角,也可以在一定程度上降低交錯分布滾子的位移振蕩范圍,如圖5d所示。

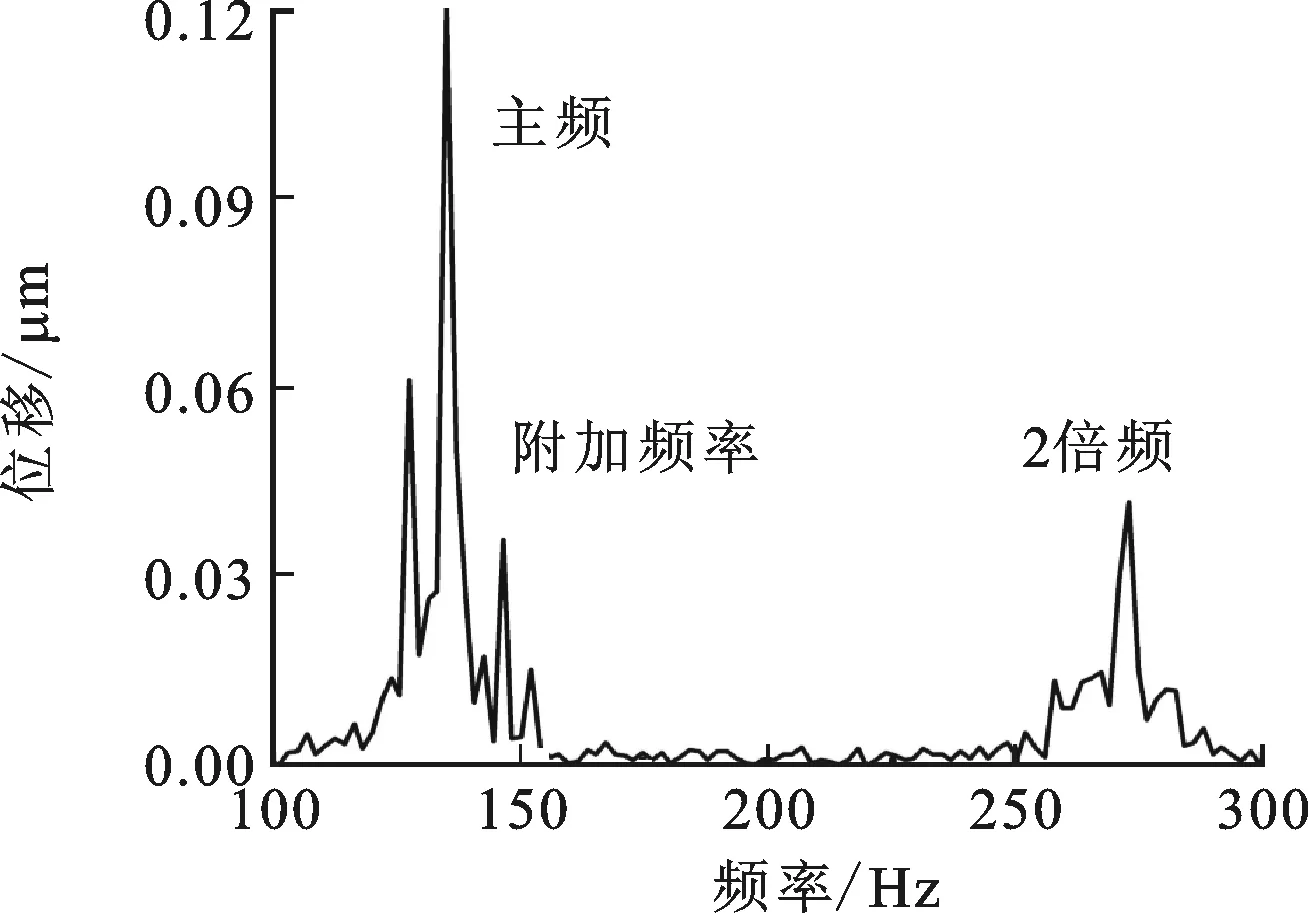
為了突出調心作用對特征頻率的影響,避免外部載荷對特征頻率幅值的干擾,將圖6仿真中載荷初始值設定為徑向載荷為20 kN,軸向載荷為200 N。

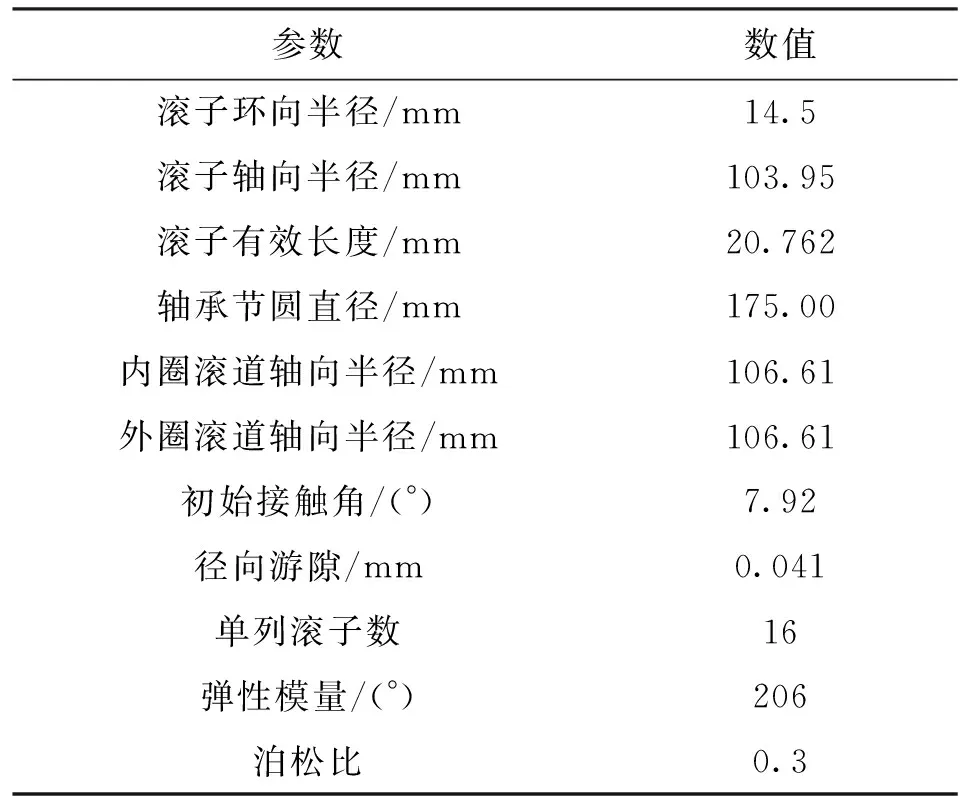
表1 軸承幾何參數與材料參數

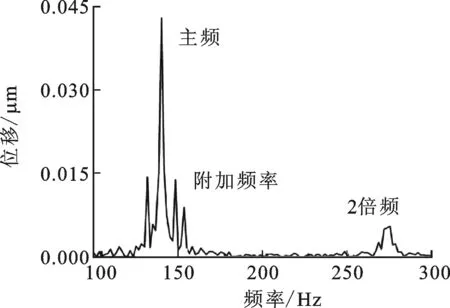
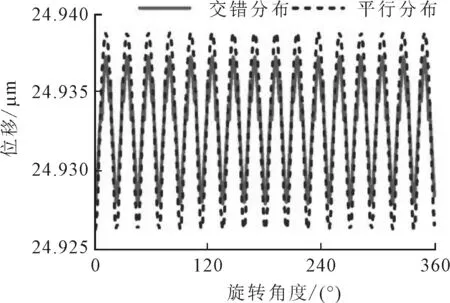
(a)交錯分布且自調心角為-2°

(b)平行分布且自調心角為-2°

(c)交錯分布且自調心角為3°

(d)平行分布且自調心角為3°

由圖6軸承振動的頻域特征對比可以看出,不論滾子是交錯分布還是平行分布,特征頻率(主頻)都約等于單列某一滾子通過外圈某一點的頻率,即約等于單列滾子數與滾子公轉頻率的乘積。從主頻的幅值上看,當軸承處于調心工況時,交錯分布的滾子更利于軸承服役的穩定性。不論是交錯分布還是平行分布,在調心作用明顯的情況下,都會激發出附加頻率,頻率值約為主頻加、減滾子公轉頻率的整數倍。總結上述規律可得附加頻率的頻率值表達式如下

fa≈fr±qfc

(28)

式中:fa為附加頻率的頻率值;fr為轉子的頻率值,即主頻;q為一個正整數;fc為滾子公轉頻率。通過對附加頻率的判別,可以確定球面滾子軸承是否處于調心工況。

2.2 滾子載荷分布

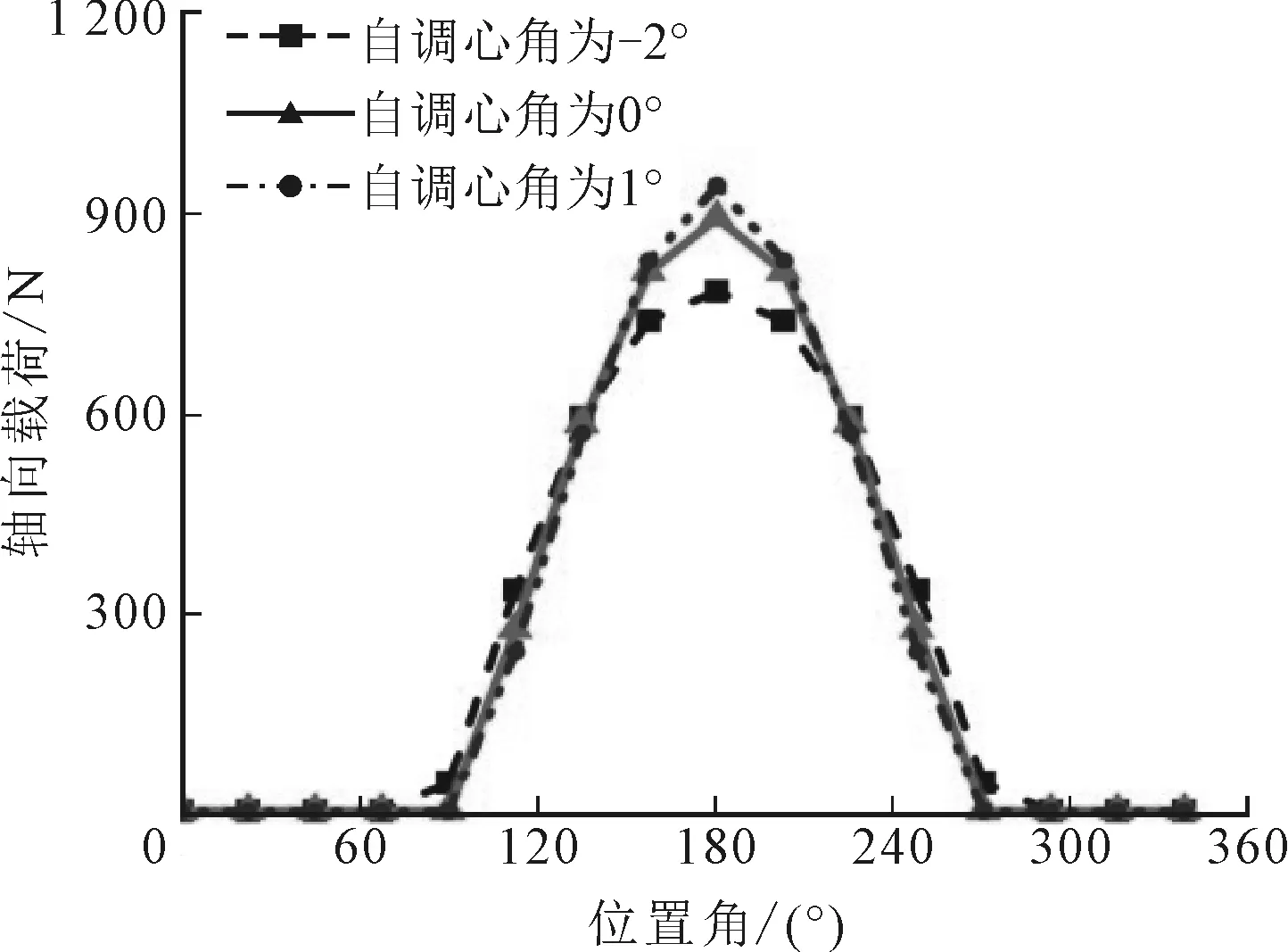
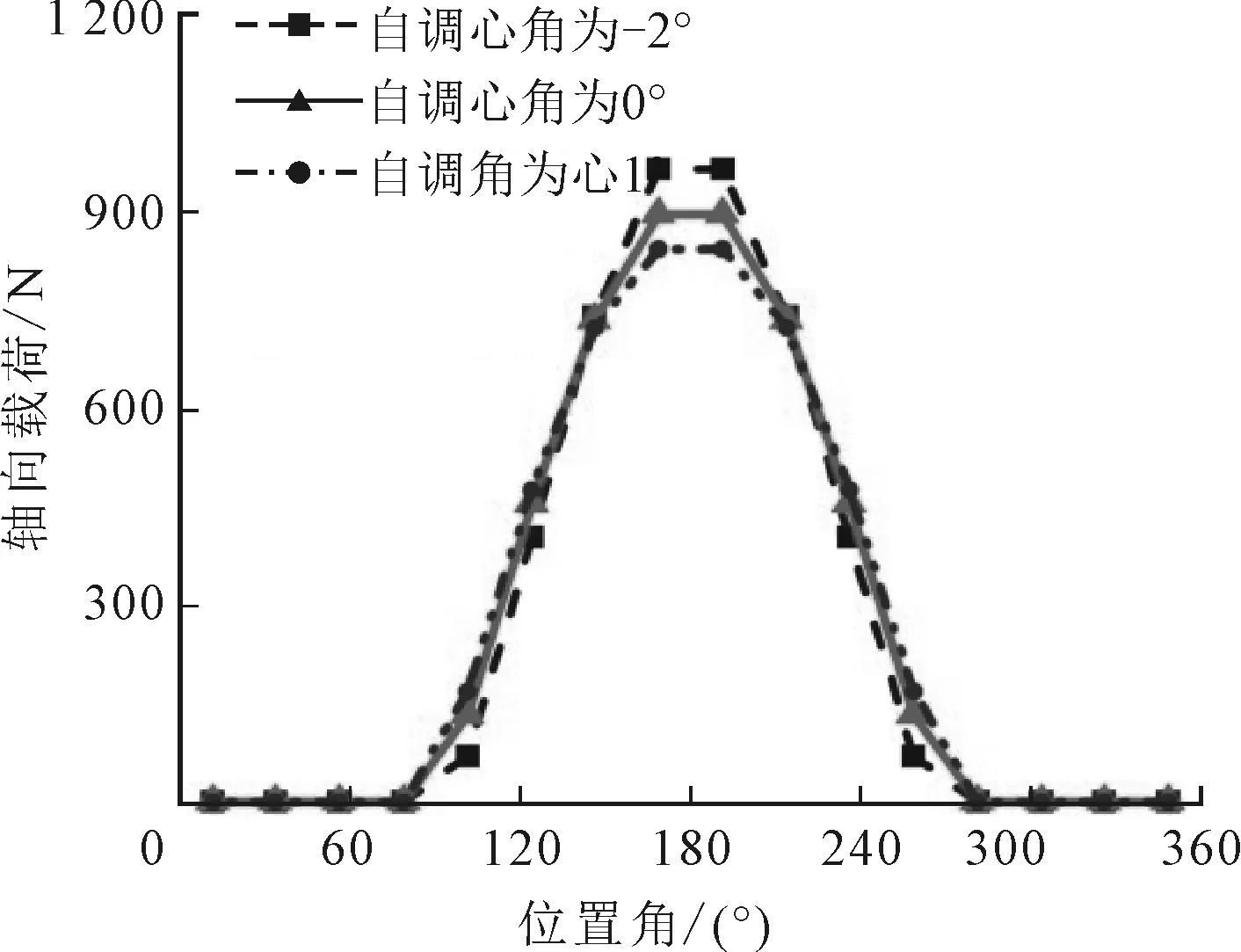
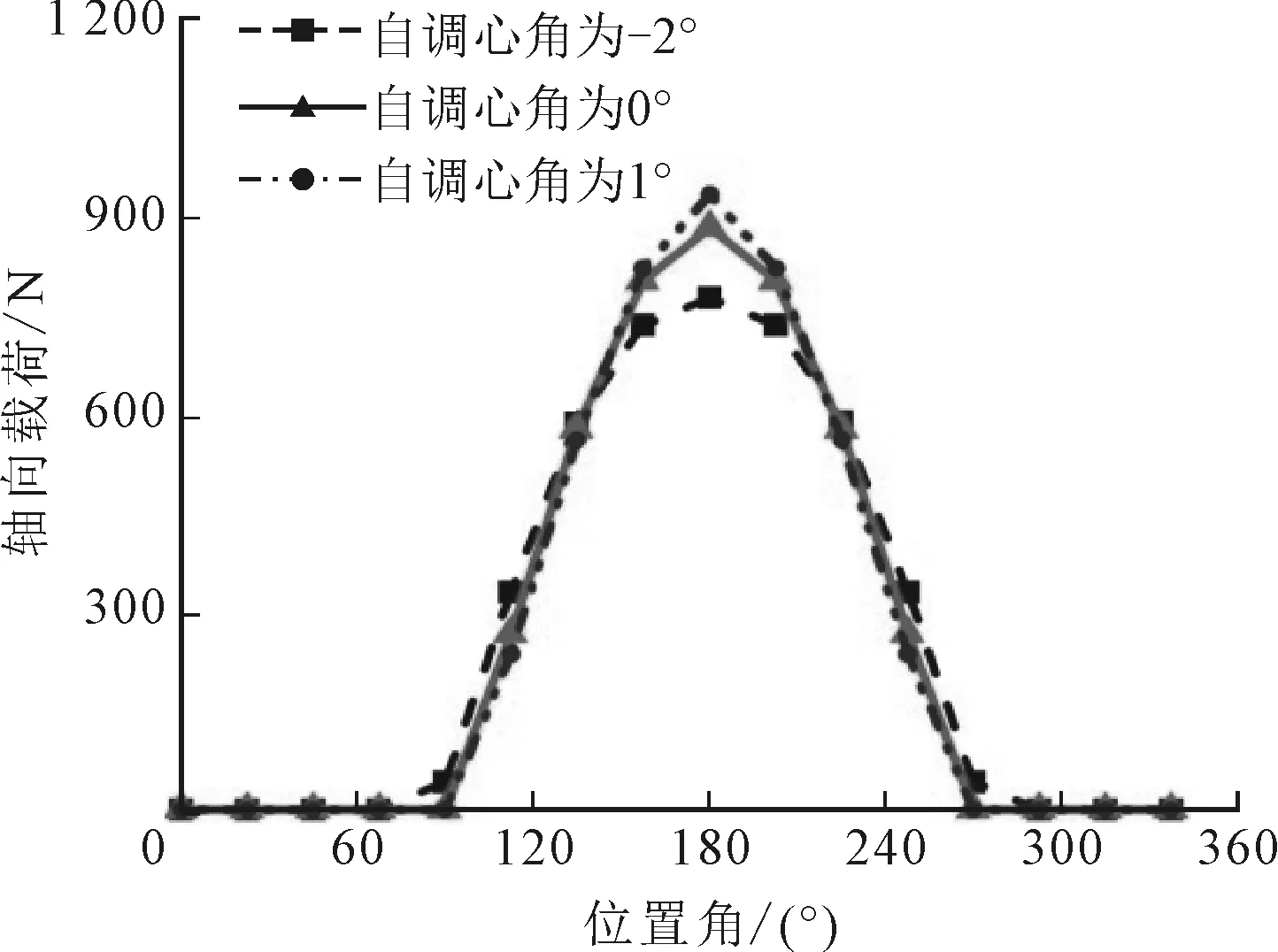
假設軸承在某一時刻受到50 kN的徑向載荷,以及200 N的軸向沖擊載荷。鑒于軸向載荷對球面滾子軸承的服役特性影響較大,圖7列舉了此種工況下軸承滾子的軸向載荷分布,可以看出,兩種滾子分布形式下的軸向載荷分布情況大致相同。說明由于滾子分布方式不同所造成的軸承振動差異并不是因為滾子受力不同,而是不同滾子分布形式下,滾子通過承載區的狀態不同所造成的,即一種是交替通過,另一種是并排跨越通過。

(a)交錯分布方式下左側列載荷分布

(b)交錯分布方式下右側列載荷分布

(c)平行分布方式下左側列載荷分布

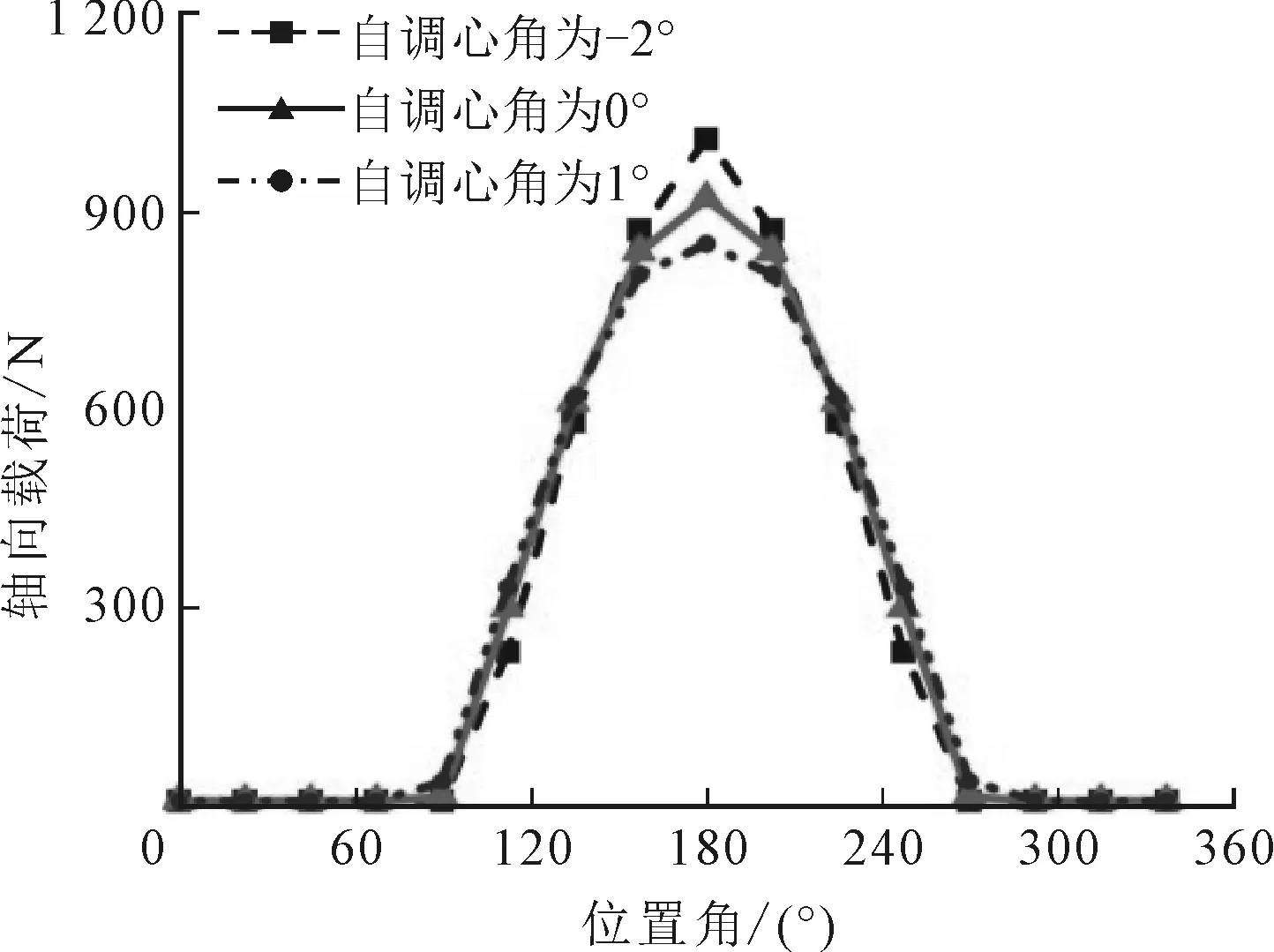
(d)平行分布方式下右側列載荷分布

由圖7還可以看出,自調心作用會導致兩列滾子受力不均,即出現偏載情況,偏載的方向會因調心角度的不同而不同。軸向力本身也會使軸承出現偏載情況,因此當以上兩種因素疊加時,會出現偏載加劇或抵消兩種結果。

考慮到球面滾子軸承存在一定的初始接觸角,部分徑向載荷會因為接觸角而轉化為軸向力,因此單個滾子所受的軸向力有大于外部軸向沖擊載荷的可能。

3 實驗驗證

待測試軸承為22215型斯凱孚(SKF)軸承和瓦軸(ZWZ)軸承,見圖8。ZWZ軸承屬于滾子交錯分布的形式;SKF軸承兩列滾子之間沒有約束關系,因此并不完全屬于滾子平行分布,但在安裝過程中,盡量使對應滾子保持平行狀態。

圖8 待測試軸承

實驗臺的總體布局如圖9所示。轉子由兩個參數相同的滑動軸承所支撐,轉子后端由電機帶動旋轉,前端預留位置布置待測軸承。實驗設計原理如下,將軸承座的內圈卡具固定在轉子上,并依次在內圈卡具上安裝待測試軸承和外圈卡具,外圈卡具不加任何約束,僅通過球面滾子軸承內外圈之間的幾何結構進行調心。這樣設計的好處在于即使在實驗室條件有限的情況下(施加的外載荷有限),也能實現調心工況。缺點在于,由于軸承座的內圈卡具并非完全約束,會隨著轉子進行小幅振動,而外圈卡具為了實現調心工況,沒有施加任何約束,屬于浮動狀態,因此得到的測試結果偏大。在自調心軸承座的外圈卡具上設有吊環,通過吊環連接加載裝置,包括拉力傳感器、加載支架以及質量塊等等,以加載裝置8沿徑向垂直方向(縱向)提供外部徑向載荷。位移傳感器分別從徑向水平(橫向)和徑向垂直(縱向)兩個方向對軸承振動信號進行采集,并將采集到的數據實時傳輸到電腦中進行處理并保存。

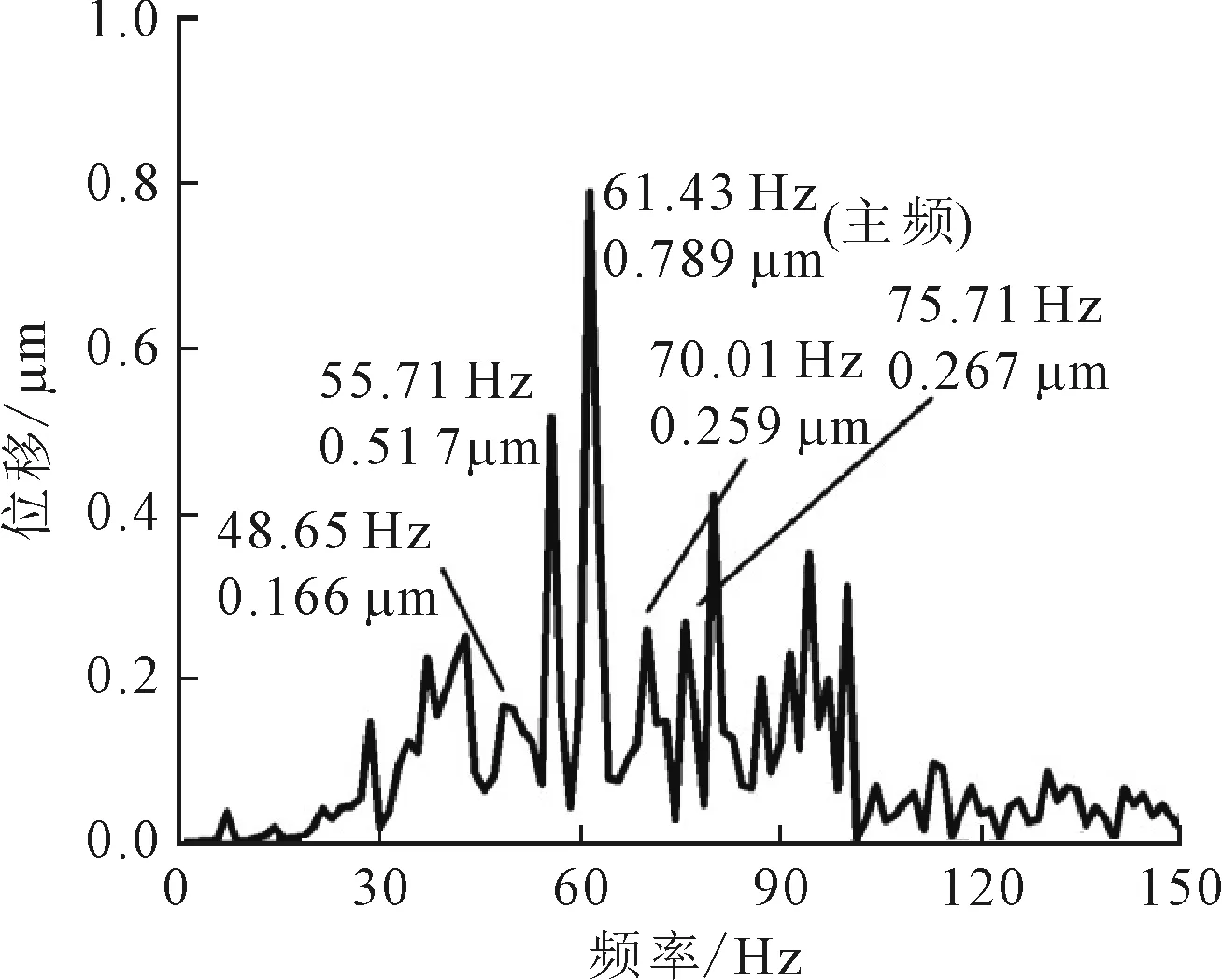
實驗工況如下,待測試軸承為22215型球面滾子軸承,實驗過程中,軸承受到徑向載荷約為430 N,轉子轉速約為320 r/min,測試結果如圖10所示。從圖可以看出,兩種軸承的主頻都約等于單列某一滾子通過外圈滾道的頻率,且交錯分布滾子所對應的主頻幅值較低。另外,在軸承服役過程中,由于調心作用所引起的附加頻率也較為明顯,附加頻率約等于主頻加、減滾子公轉頻率的整數倍。該結論與圖6和式(28)所得出的規律相符,從而證明了本文理論計算結果的合理性。