移動邊緣計算中分布式的設備發射功率優化算法

周文晨,方維維,李陽陽,薛峰,王子岳

(1.北京交通大學計算機與信息技術學院,100044,北京;2.中國電子科學研究院創新中心,100041,北京)

近年來,移動互聯網快速發展,移動用戶設備數量呈指數爆炸式增長[1],移動計算需求不斷升級。根據思科公司最新預測報告顯示,2021年全球移動數據流量將比2016年增長7倍,全球移動設備數量將增加到116億[2],但目前以長距離數據傳輸和集中式大數據處理為特點的移動云計算不僅占用大量網絡帶寬,而且傳輸時延較大,已無法滿足時延敏感型業務,例如無人駕駛汽車、醫療大數據和智慧城市等的需求[3]。

歐洲電信標準化研究所(ETSI)在2014年首次提出移動邊緣計算(MEC),移動設備可將高復雜度、高能耗計算任務卸載到MEC系統的接入網邊緣節點,例如基站、無線接入點等,從而獲得低時延、近距離的本地化云服務[4]。MEC系統結合了移動通信[5]和云計算[6]兩種技術,通過協同優化通信和計算資源實現低能耗、低時延的計算卸載服務。目前,最新的MEC系統研究將關注點放在單服務器多用戶條件下的通信、計算資源分配控制,以實現總體能耗最優。Mao等基于隨機優化模型的優化方法,聯合本地計算功率、最優發射功率和無線帶寬資源等約束對移動設備能耗進行優化,但是卻無法有效約束時延,且計算復雜度較大,沒有考慮某個區域內MEC系統的整體部署優化[7];Liu等通過采用馬爾可夫決策過程理論對任務隊列的排隊屬性進行分析,提出了發射功率約束條件下的最小化處理時延的問題,但忽略了設備的能耗[8];You等針對TDMA、OFDMA兩種網絡工作模式,通過確定卸載量和時間槽,解決卸載通信和本地計算總體能耗最小化的凸優化問題,但是所提算法需要依賴于本機計算能量和信道增益的先驗知識做出資源分配策略,降低了實際場景的可用性[9]。

綜上所述,本文以MEC系統的多服務器、多用戶的大規模場景下的計算卸載的時延和能耗的平衡為研究目標,基于邊緣計算的通信和計算資源的耦合約束,設計一種基于馬爾可夫近似的分布式發射功率優化算法(TPO)。該算法基于馬爾可夫狀態概率跳轉規則設計,移動用戶設備自主決策計算卸載的服務器對象,從而有效降低系統級用戶功耗。理論證明,分布式TPO算法具有穩態概率分布的馬爾可夫鏈,所設計的轉移速率滿足馬爾可夫鏈的狀態相互轉換條件;實驗仿真結果表明,所提算法顯著優于基準算法,并在有效時間內逼近最優解決方案。

1 MEC系統建模

本文研究的MEC系統場景示例如圖1所示。根據已有的相關研究,本文基于以下5種假設:①每個邊緣服務器時間和頻率完全同步;②每個邊緣服務器上的每個載波的信道增益在特定時間內保持恒定;③由于每個邊緣服務器的載波頻率不同,假設MEC系統中邊緣服務器間不存在信號干擾;④設備同一時刻只能與一個邊緣服務器進行連通;⑤卸載所需要執行的指令都可以利用邊緣服務器進行處理[10-13]。

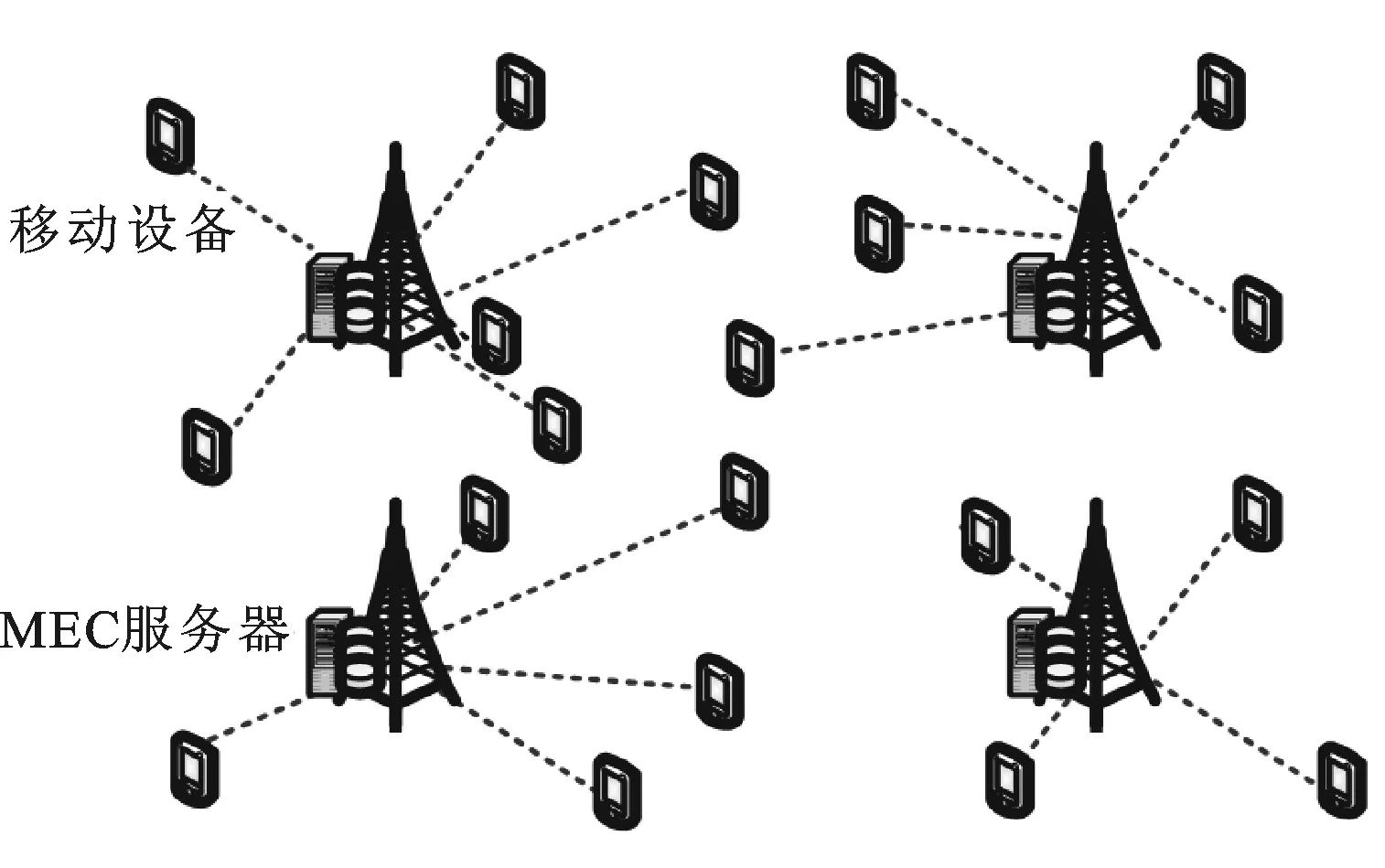
圖1 多MEC服務器多用戶設備場景示例

假設當前區域內有M個邊緣服務器X={1,2,…,M}和N個移動用戶設備Y={1,2,…,N}。每個移動用戶設備n的計算任務卸載到邊緣服務器m,設備n必須傳送所有信息到服務器m。設定執行程序的參數:①每秒輸入比特數;②需要被MEC服務器執行計算的指令集;③每秒輸出比特數。對于移動用戶設備n所需要卸載到服務器m的計算任務的輸入數據大小為Cmn,執行的指令數為Dmn=Dmn(Cmn)。設備n是否卸載計算任務到服務器m主要取決于如下因素:需要被處理的指令數、設備n與對應服務器m之間的無線信道狀況和服務器m的并行多個進程的能力大小,同時每個進程為了用戶的滿意體驗都規定了不應超過的最大時延[14],因此移動用戶設備n決定卸載計算任務到服務器m之前必須考慮時延約束。在沒有解碼錯誤的前提下,用戶設備n的時延應該包含將輸入信息傳輸到對應服務器m的時間、服務器m執行指令所需的時間和將結果返回給設備n的時間。

根據香農定理,在加性白高斯噪聲(AWGN)、信道帶寬為B的信道上傳送Cmn數據所需的最小時間為

(1)

式中:Pn是設備n計算任務卸載的發射功率;|Hmn|2是信道衰落系數(歸一化距離);Gmn是信噪比裕度;dmn是設備n和相連MEC服務器m的物理距離;γ是路徑損耗指數;N0是噪聲功率。Pn是可調功率,Pn∈S,S是有限離散集合。

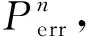
(2)

服務器m執行指令所需的時間與其資源分配方式有直接關聯。系統內用戶設備與服務器的連接方式表示為

(3)

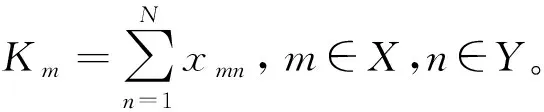
(4)

忽略服務器m把計算結果返回給設備n的極短時間[11],則設備n的平均計算卸載的時延為

(5)

(6)

Pn∈S,n∈Y

xmn∈{0,1},m∈X,n∈Y

基于香農定理和鏈路傳輸特性將用戶功率最小化策略建模成問題(6),作為典型的組合網絡優化問題,其求解復雜度是NP難的,一般只能通過集中式的窮舉搜索獲得最優解[15],可行解空間隨著網絡規模的增大而呈指數級增加,而隨機法又不能獲得穩定而較優的解,因此有必要尋求一種有效和穩定的求解方法。

2 TPO算法設計

針對問題(6),設計了一種分布式并發的優化算法,利用Log-Sum-Exp函數[15]將問題轉化為最小權重配置的近似問題,然后使用馬爾可夫近似[15]求解問題,即通過求解轉化后的問題從而趨近問題(6)的最優解,并證明算法可進行有效求解。

2.1 Log-Sum-Exp原則

設定配置f={xmn,m∈X,n∈Y},即問題(6)所表示的系統中移動用戶設備n和邊緣服務器m相連的可行配置狀態,所有可行的狀態f組成F,即f∈F,則問題(6)的等效問題模型是

(7)

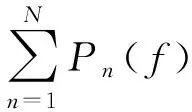
問題(7)是NP難的網絡組合優化問題,對實際系統來說可行集合F非常大,因此通過Log-Sum-Exp函數,將問題(7)近似轉化為

(8)

式中β是正的常數。因為問題(8)的目標函數對于所有的ρf是二次可微、單調遞增和嚴格的凹函數,其所有的約束都是線性的,所以Karush-Kuhn-Tucker(KKT)條件對于最優解是必要和充分的,故問題(8)的最優解是

(9)

與原問題(6)相比,近似問題(8)存在一個額外的熵項,即為優化差距,通過對比兩問題的表達式可知優化差距的上限是

(10)

從式(10)可知,優化差距上限的大小取決于β,當β增加時,優化差距上限會減小,這意味著近似求解結果更加準確,優化差距上限r*=lb|F|/β,此時ρf=1/|F|,f∈F,同時由文獻[16]可知,當β增加時,收斂時間將增加。

綜上可知,當β增加時,近似求解獲得的系統移動用戶設備發射總功率更加準確,因此選擇相對較大的β來獲得穩態分布。通過馬爾可夫近似獲得的近似系統功率可表示為

(11)

2.2 TPO算法設計

根據文獻[15]可知,狀態轉移速率有很多設計選擇,將其設計為

(12)

馬爾可夫鏈通常具有分布式的結構,因此可以設計分布式算法以實現符合馬爾可夫鏈的移動用戶設備的決策算法[17]。算法設計的關鍵是建立不同配置f之間的鏈接,實現最小化轉換配置的系統級功率,通過每次只執行一個用戶設備切換服務器的選擇來連接系統兩個配置的鏈接。本文將算法命名為發射功率優化(TPO)算法,TPO算法分為以下4個步驟。

步驟1每個移動用戶設備隨機選擇MEC服務器,初始化計算資源和設備時延約束等信息。

步驟2當前狀態定義為配置f,每個用戶設備計算自己的發射功率并廣播,同時生成均值為ζ的指數分布隨機數,根據隨機數進行倒計時,最先到期的用戶設備n將隨機切換到新MEC服務器,并通知其他所有用戶設備終止倒計時。

步驟3進入新配置f′,每個用戶設備重新計算自己的發射功率并廣播。用戶設備n根據配置f和f′的系統移動用戶設備發射總功率的改變做出決策,以概率ρf,f′停留在新的MEC服務器或者以概率(1-ρf,f′)切換到原先的MEC服務器,其中

(13)

步驟4重復步驟2～步驟4,直至收斂。

2.3 TPO算法可行性證明

定理1TPO算法實現了一個時間可逆的馬爾可夫鏈,其穩態分布如式(9)所示。

證明通過算法步驟2的移動用戶設備的轉換條件可知,所有配置可以在有限轉換次數內相互可達,因此構造的馬爾可夫鏈是不可約的。此外,它是具有唯一穩態分布的有限狀態遍歷馬爾可夫鏈。現在證明穩態分布表達式是式(9)。

基于式(12)設定的系統狀態轉移速率可得

(14)

它滿足細致平衡等式,證畢。

定理2通過上述完備的馬爾可夫鏈設計,對于任意兩個滿足相互轉換條件的配置f,f′∈F,轉移速率是式(12)。

證明從系統的角度來看,狀態f轉移到狀態f′是由于配置f下的設備n切換服務器所致,設備n從已連接的MEC服務器斷開,隨機切換到新的服務器,可切換的服務器有M-1個。故對于設備n離開狀態f轉移概率為

其中配置f∈F是馬爾可夫鏈的狀態之一,因為設備根據均值為ζ的指數分布隨機數進行倒計時,倒計時結束后進行服務器切換,因此狀態f轉移到狀態f′的轉移速率為

因此,轉移速率與式(12)相等,證畢。

本文算法滿足近似最優解,是可行設計。

3 仿真與結果分析

3.1 實驗設置

為了驗證TPO算法的有效性和穩定性,采用C++編程進行仿真實驗,與隨機法和窮舉法的實驗結果進行對比,得到關鍵參數對系統的影響。參數設置見表1[11,18]。移動用戶設備n的輸入數據大小Cmn設定為(0.2+0.02n)MB,為簡化起見,設定MEC服務器執行的指令數Dmn與輸入數據大小Cmn成線性相關,即Dmn=σCmn。集合S={0w,10-2w,2×10-2w,…,10w}。

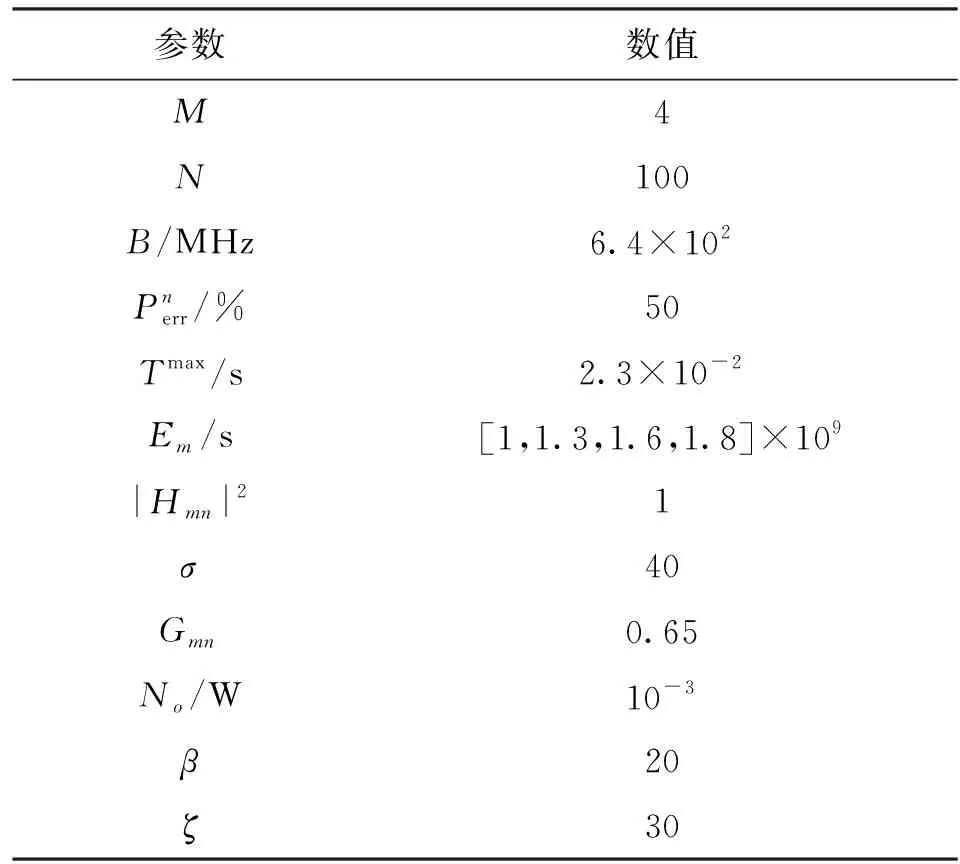
表1 TPO算法仿真參數

3.2 實驗結果分析

因采用窮舉搜索獲得系統N個移動用戶設備與M個MEC服務器的連接方式的最優解共需計算MN次,復雜度過高,因此我們將TPO算法與隨機法實驗結果進行對比。圖2分別給出了TPO算法與隨機法得到的系統用戶設備發射總功率。從圖2可知,雖然TPO算法實現的系統用戶設備發射總功率平均值在算法執行初期比隨機法平均值大,但是在50次迭代后小于隨機法平均值。TPO算法實現的總功率均值隨著算法迭代次數逐步下降,可收斂至4.6 W,而多次隨機法的均值為21.4 W,由此可推算出TPO算法性能比隨機法的效果提升了78.5%,因此TPO算法不僅可行,并且得到的收斂解比隨機法結果更趨近最優解,更加有效。

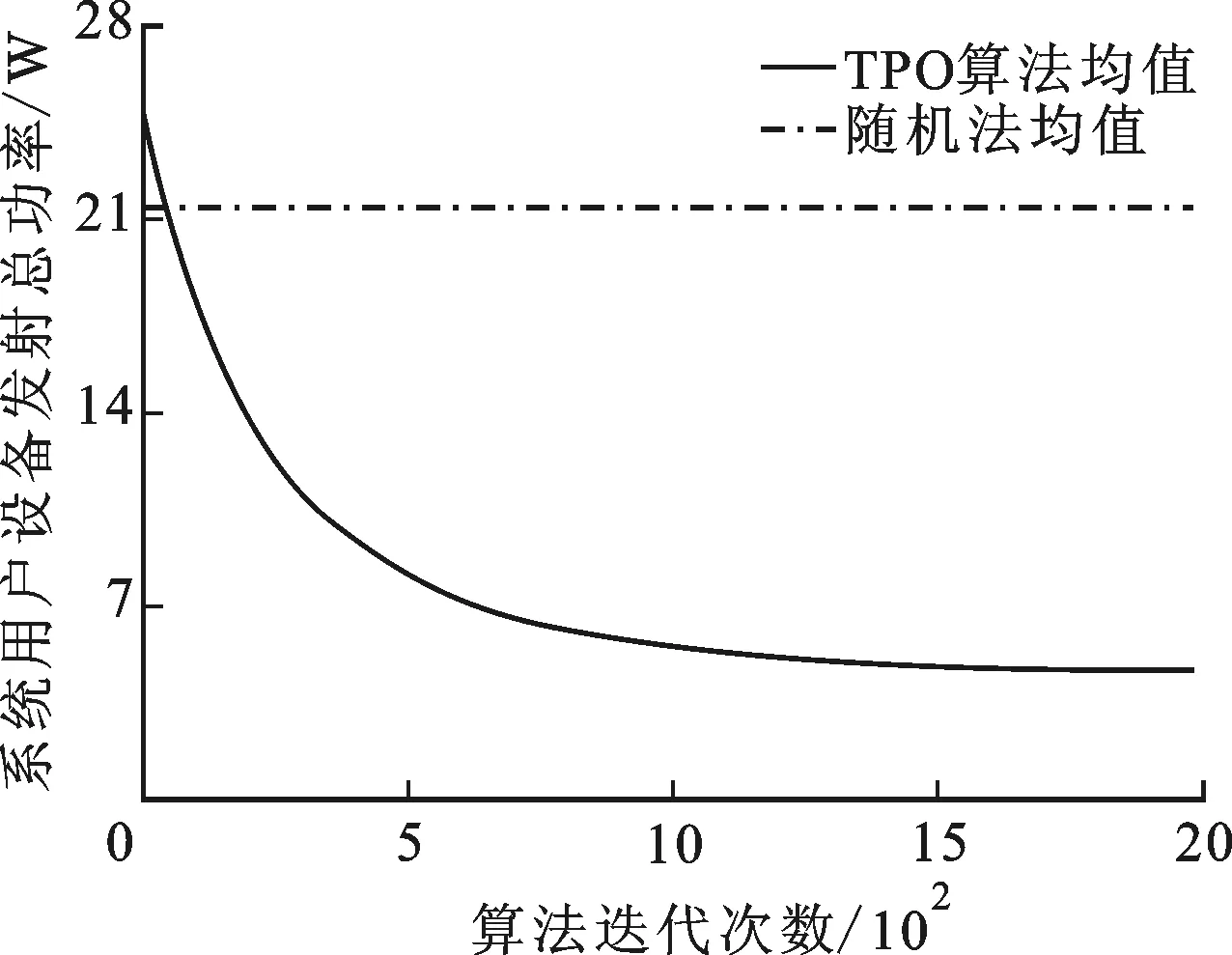
圖2 TPO算法與隨機法對比

為了進一步驗證TPO算法的準確性,建立4個MEC服務器服務10個用戶設備的小型MEC系統場景,在此場景下對比分析TPO算法多次實驗平均值和窮舉搜索最優結果。圖3給出了TPO算法與窮舉搜索實現的系統用戶設備發射總功率。實驗數據顯示,TPO算法實現的系統用戶設備發射總功率均值僅在第130次迭代后逼近最優解,遠小于理論優化差距,與窮舉法的410計算次數相比,TPO算法復雜度大大降低,更具有實際應用價值。

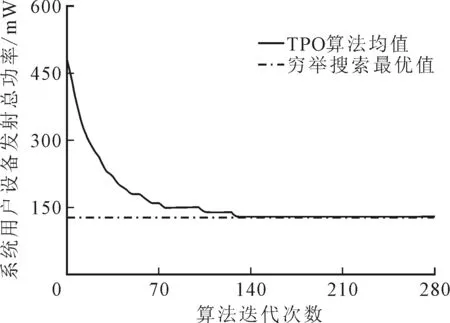
圖3 TPO算法與窮舉搜索結果對比

以上實驗結果驗證了TPO算法的有效性和實用性,下面將分析系統關鍵參數對TPO算法結果的影響。圖4顯示了TPO算法的參數β對算法收斂時間和系統用戶設備發射總功率的影響。從圖4中可知,當β=20時,系統總功率接近最優解,收斂時間較長;當β=5時,系統總功率遠離最優解,收斂時間較短。因此伴隨β的增加,TPO算法獲得的近似系統總功率越接近最優值,同時收斂時間增加,符合式(10)理論結果。

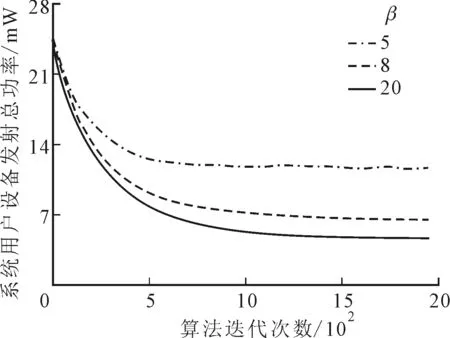
圖4 系統用戶設備發射總功率與β的關系

圖5是將所有移動用戶設備的輸入數據大小Cmn設定為相同值并統一調整,觀察系統用戶設備總功率與設備所需計算卸載的輸入數據量大小Cmn的關系。從圖5可以看出,當Cmn越大,TPO算法實現的系統用戶設備的總發射功率會增大,這是因為設備需要更多的能耗傳輸更多的數據,但是總發射功率的收斂時間并沒有伴隨Cmn增加發生顯著變化,說明當設備的輸入比特量增加時,TPO算法的收斂速度會更快,這對實際系統中用戶設備計算卸載高峰期的處理具有很大的優勢。

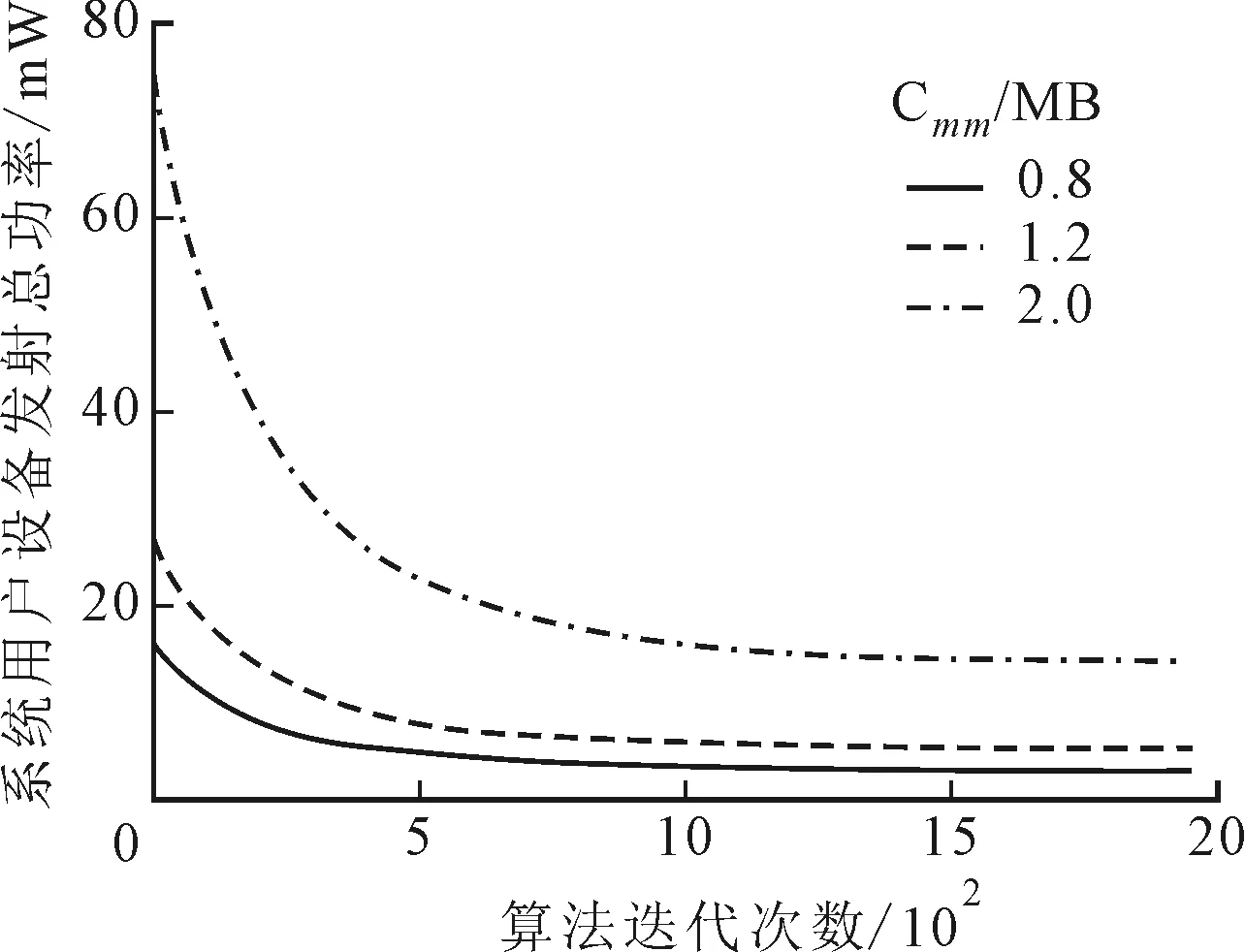
圖5 系統用戶設備發射總功率與Cmn的關系

為了顯示TPO算法對用戶設備資源分配的調節效果,建立了用戶設備高度聚集的特殊場景,將TPO算法與其他常用算法的處理效果進行對比。通過觀察可知,圖6b中傳統的依賴接收信號強度指示(RSSI)進行連接的方式會導致MEC服務器資源分配不合理,進而無法滿足用戶需求,圖6c中隨機法實現的系統設備發射總功率為48.3 W,圖6d中TPO算法實現的系統設備發射總功率僅為8.7 W,因此隨機法的實驗結果不滿足最小化目標,而本文提出的TPO算法能夠合理有效地建立移動用戶設備和MEC服務器的連接,達到系統設備發射總功率優化的最優效果。

(a)用戶與基站位置 (b)RSSI連接方式

(c)隨機法連接方式 (d)TPO算法連接方式

4 結 論

傳統的云計算模型已無法有效解決海量的邊緣數據計算卸載問題,如何提升移動邊緣計算的大規模網絡架構的計算卸載的效率和用戶體驗受到越來越多的關注。本文在傳輸帶寬和計算資源參數化的基礎上,使用馬爾可夫近似框架將系統用戶設備的發射功率最小化問題轉化,設計分布式的發射功率優化算法求得原目標的近似最優解。對比基準算法測試結果,TPO算法的系統用戶設備發射總功率優化效果比隨機法提升了78.5%,同時執行效果更加穩定;與窮舉搜索的指數階O(2n)計算復雜度相比,該算法的復雜度為線性階O(n),故該算法在有限迭代輪次后即可逼近窮舉搜索的最優解;與傳統的RSSI連接方式相比,TPO算法能夠避免在用戶量小范圍高度集中時爭搶計算資源的現象,減少網絡擁塞和資源分配不均衡的情況發生,滿足用戶計算卸載需求。TPO算法能夠在保證用戶設備的時延約束下有效降低系統用戶功耗成本,確保時延敏感型業務的時延約束下的用戶體驗。