考慮內外均衡安全增益的可量化社區隱藏算法

趙 霞 魏霖靜 肖 君

1(甘肅農業大學信息科學技術學院 甘肅 蘭州 730000)2(甘肅省計算中心系統集成部 甘肅 蘭州 730000)

0 引 言

網絡遍布于我們的日常生活中，網絡的研究涉及到許多學科，從物理學到計算機、社會科學等諸多方面。網絡分析中的一個重要任務是社區檢測識別，即網絡的區域(頂點子集)劃分，以幫助其了解網絡本身的結構和特征。

雖然社區檢測研究非常廣泛的課題，但很少有技術能夠允許從社區檢測算法中隱藏目標社區。本文研究的目的是提供這個問題的深入解決策略，稱之為社區隱藏。可以從兩個不同的層面對這個問題進行研究。隱藏技術對于想在Facebook或Twitter等社交網絡中隱藏(作為群體)的用戶是有用的。有觀點認為，想要隱藏的社區不應該是網絡的一部分，而從隱私權的角度，很多網絡中的個體節點希望不被網絡檢測工具檢測到。研究社區隱藏的另一個意義是：針對惡意目的的社區檢測攻擊，可以研究其作用機理，制定出有效的防御機制。在研究社區隱藏過程中，存在下列需要解決的問題：(1) 隱藏模型問題。這里通過關注成員節點所擁有的真實的網絡知識量將社區隱藏問題處理為優化問題。然后，引入社區安全性指標，以隱藏函數作為優化目標。研究表明，基于最優模塊化的社區隱藏策略需要對社區結構具有先驗知識，這取決于產生這些社區的社區檢測算法[2]。基于安全性的社區隱藏不會受到這個問題的影響。(2) 如何量化特定目標社區的檢測算法的欺騙水平。通過引入隱藏指標，給出這方面的形式定義。(3) 高效算法的設計。社區安全性指標的高值優化，某種方法可以搜索所有可能的候選，但可能計算效率不符合要求。

本文研究的目的是展示在各種真實網絡上，通過不需要全局網絡知識的近似優化技術，可以找到好的隱藏解決方案。該算法可擴展到具有數百萬個節點和邊緣的網絡，并且比社區檢測算法快得多，能夠先于社區檢測網絡算法完成社區的隱藏操作[3]。

1 社區檢測隱藏問題描述

本節將描述社區隱藏問題，并提供一個問題示例。首先從一些初步的定義開始。網絡G=(V,E)是一個無向圖模型，其中V是網絡模型的節點集，E是網絡模型的邊集。

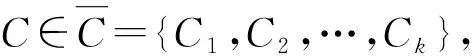
(1)

類似地，可定義精度指標為:

(2)

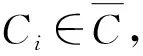
(3)

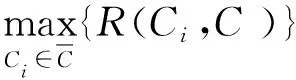
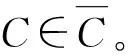
2 考慮安全增益的可量化社區隱藏

2.1 社區隱藏問題模型

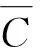
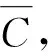
定義2(社區隱藏)令網絡模型為G=(V,E)，給定目標社區C∈V，以及更新的預算β，則解決社區隱藏問題等于求解以下優化問題：

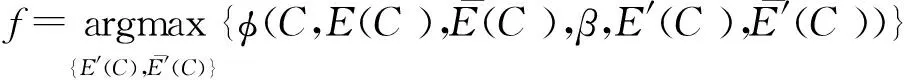
(4)

式中：函數φ(·)模型是一種社區隱藏算法；預算β限制了邊緣更新的數量。隱藏函數φ與隱藏得分H的關鍵區別在于前者選擇最大化φ的β變化，而H可量化目標社區C的理想屬性(盡可能隱藏在檢測算法的輸出中)[6]。

2.2 社區檢測隱藏算法框架

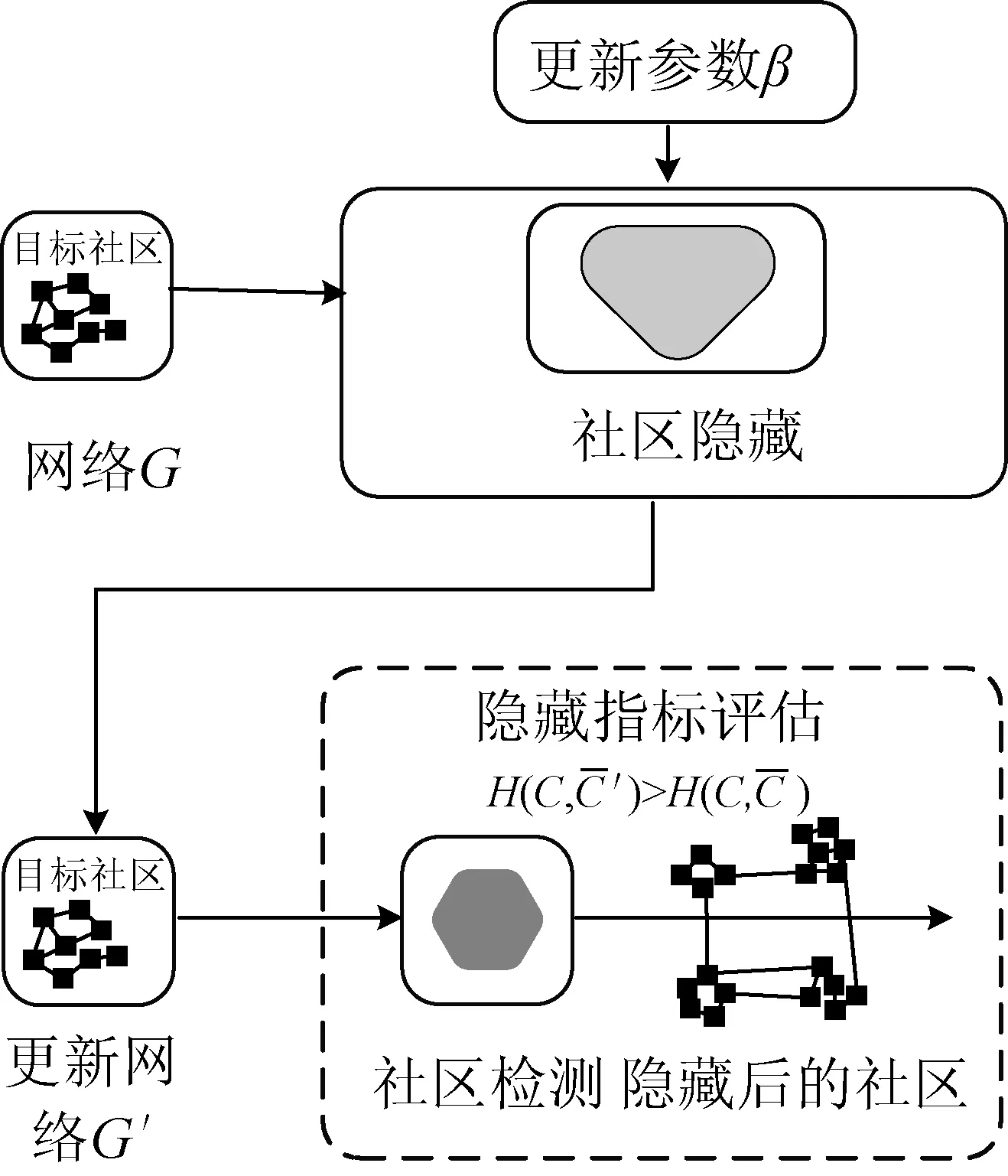
圖1 社區隱藏過程

2.3 算法描述

本文的社區隱藏算法見算法1。算法1只考慮了C內邊緣添加，而不考慮C間邊緣刪除。并且，為選擇最優更新，僅需獲得C內邊緣/節點度即可[8]。因此，算法所需的網絡知識量是有限的。

算法1基于安全性的社區隱藏

1. procedure COMDECEPTSAFENESS(G=(V,E),C,β)

3.np=getNodeMinimumAddRatio(C)；

4.nt=findExteralNode(np,C,G)；

6. (nk,nl)←getBestDelExclBridges(C)；

9. G←(V,E∪{(np,nt)})；

11.G←(V,E{(nk,nl)})；

12.β=β-1；

13. endwhile

算法1中，第3行getNodeMinimumAddRatio()可對于每個n∈C，計算在C以外的n個邊緣的分數。第4行的findExteralNode()目的是找到邊緣(np,nt)不存在節點的。第6行getBestDelExclBridges()分兩個階段執行；獲得最佳的邊緣鏈接；選擇最方便的邊緣更新，并將其應用于網絡。最佳的節點添加和邊緣刪除策略，主要是基于式(4)所示的優化目標函數進行執行，具體可通過以下實例進行描述，如圖2所示。

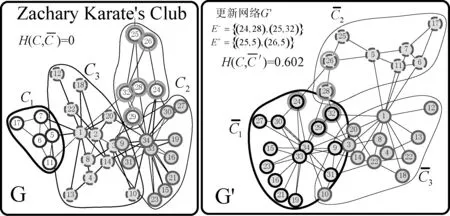
(a) 空手道俱樂部網絡 (b) 更新網絡模型圖2 算法應用實例

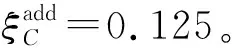
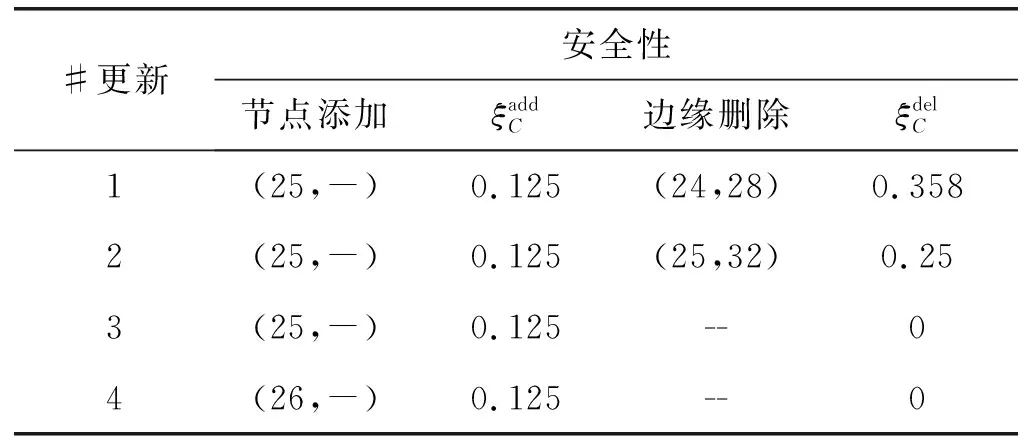
表1 網絡更新計算過程

對于給定社區C和參數β，算法1對初始網絡G進行更新，得到更新后的網絡G′，滿足σ(C′)≥σ(C)。對于算法1所示的基于安全性的社區隱藏算法，最佳的節點添加和邊緣刪除策略，可通過檢測C中的所有節點添加和邊緣刪除計算獲得[10]，其計算復雜度為O(|C|+|E(C)|)。節點添加和邊緣刪除過程的計算復雜度為O(|E(C)|)[11]。

3 社區檢測隱藏算法的安全性分析

3.1 安全性定義

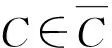
定義3(節點安全性)給定網絡模型為G=(V,E)，社區結構C?V，以及社區C成員u∈C。則G中u的安全性σ(u,C)可定義為：

(5)

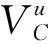
式(5)右側次項中，給出u的邊緣的一部分，并給出了u如何在網絡內隱藏其度的解釋。為了提高安全性，u應該多樣化其連接，即與不在C中的節點有較高比例的連接。同時，在區間[0，1]中對式(5)和返回節點安全性值的兩個分量進行加權。

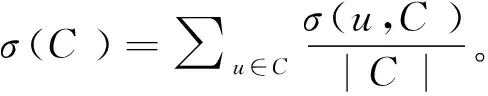
從C成員的安全性角度，允許識別最不安全的成員并重新連接其鏈接以增加整個C的安全性得分。安全性控制社區的不同屬性有可達性和內部/外部邊緣平衡。

3.2 邊緣更新對安全性的影響

1) 邊緣添加：令網絡模型為G=(V,E)，給定目標社區C∈V，C的安全性為σ(C)。令ξC=σ(C′)-σ(C)為安全增益。

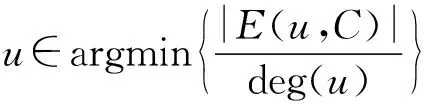
證明：檢測如果滿足ξC=σ(C′)-σ(C)≥0，則有：

(6)

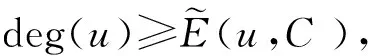
2) 邊緣刪除：本節主要從C內邊緣進行邊緣刪除操作。

定理2C間邊緣(u,w)刪除，其中u∈C，w?C，則對于給定的G′=(V,E{(u,w)})，ξC≤0始終成立。

證明：檢測如果滿足ξC=σ(C′)-σ(C)≥0，則有：

(7)

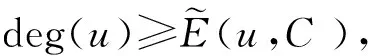
定理3社區C內邊緣(u,w)刪除，并不總是帶來安全增益。

證明：假設刪除邊緣(u,w)之后，節點u和節點w在C中仍然保持的相同連通分量。需要滿足下列條件：

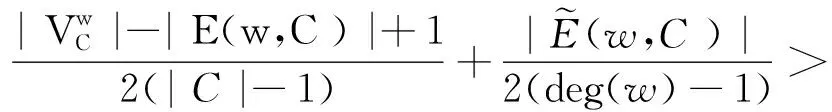
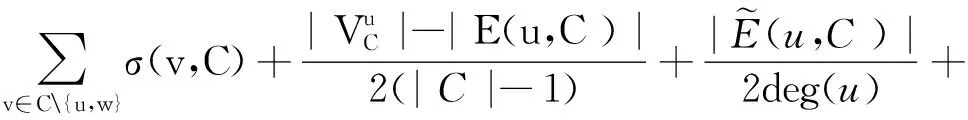
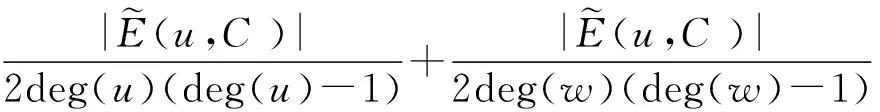
4 實驗分析

4.1 實驗設置

實驗硬件設置：CPU i7-6400K 3.0 GHz，內存大小為16 GB RAM，操作系統為Microsoft Windows 7 旗艦版[13]。考慮了基線算法，隨機地選擇更新的類型和邊緣添加/刪除的端點[14]。為了驗證本文算法的有效性，這里選取4種社區檢測算法，檢驗社區隱藏算法的效果：(1) Louvain社區檢測算法(Louv)，一種社區檢測的多級模塊化優化算法，其計算復雜度為O(|V|log|V|)；(2) InfoMap社區檢測算法(Info)，其返回一個社區結構，并為隨機游走提供了最短的描述長度，其計算復雜度為O(|E|)；(3) Edge-Betweeness社區檢測算法(Edge)，為一個層次分解過程，其中邊緣刪除過程按照評估分值的下降順序執行；(4) SpinGlass社區檢測算法(Spin)，通過最大化加權社區聚類來實現圖劃分，基于三角分析策略實現對社區檢測度量，其計算復雜度為O(|E|log|V|)。為了提高實驗結果的穩定性，以下實驗數據，為相同情形下運行上述4種社區檢測算法的結果均值。

因為沒有標準的基準來測試隱藏算法性能，這里設計了算法2中的方法進行評價。因為本文評價的是社區隱藏算法對于社區的隱藏程度，即它返回正確社區的能力與我們的目標是正交的。假設在最壞的情況下進行實驗(第3行)，即假設目標社區C被完全發現。對于具體的檢測算法，通過查看社區分布可選擇不同規模的目標社區。

算法2社區隱藏性分析

1. procedure EVALUATEDECEPTIONALGOG (β,AD,D)

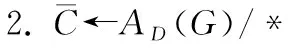
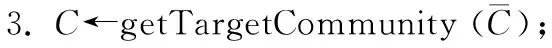
5.σ(C)←getSafeness (C,G)；

7.G′←applyDeception (G,C,β,Dx)/*x∈{s,m,r,w}*/；

10.σ(C′)←getSafeness (C,G′)；

算法2第4-6行可計算社區檢測算法的模塊性、安全性和隱藏評估得分，第7行給出的是更新后的網絡G′。算法第8行，在G′上運行算法1計算社區檢測社區的模塊性、安全性和隱藏評估得分。上述評估算法的目的是調查：(1) 社區隱藏算法如何從檢測算法中隱藏社區C；(2) 如何設定參數β；(3) 社區隱藏算法對社區結構的影響；(4) 社區隱藏和檢測算法的運行時間。

4.2 結果分析

本文選取的實驗網絡有Zachary Karate’s Club(kar)、Dolphins association(dol)、Madrid Train Bombing(mad)、Books about US politics (polb)4種實驗網絡。表2給出了所考慮的網絡的概述和選取的4種檢測算法發現的社區數量。

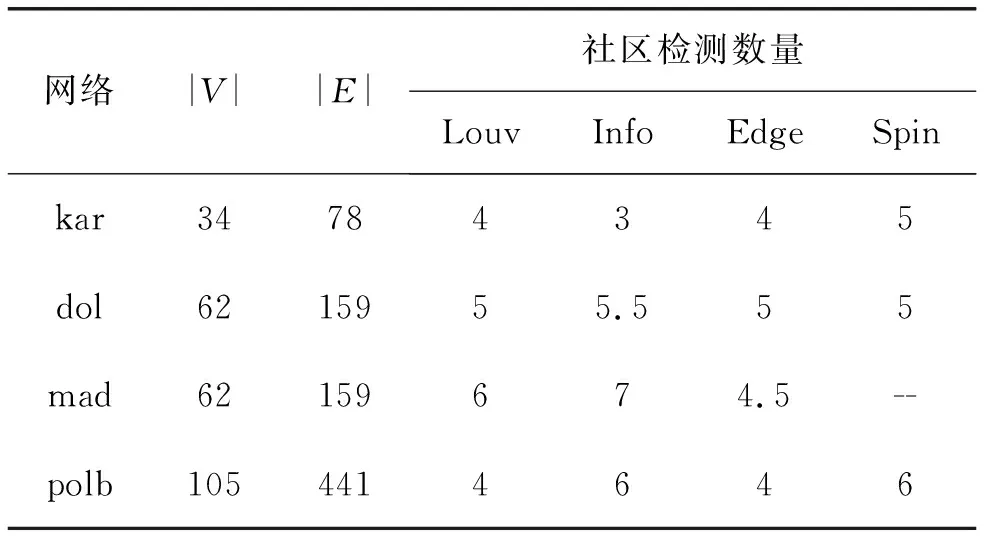
表2 真實網絡情形

表2中，給出的4種檢測算法發現的社區數量存在一定的差異，這與算法的檢測性能相關。上述實驗數據出現小數的原因是本文選取運行20次的結果均值計算結果。SpinGlass社區檢測算法在mad網絡上的社區發現數量未得出，主要原因是該算法不能處理一定規模以上的網絡。針對表2所示實驗網絡，參數β的取值區間是1～5，圖3給出實驗所得的社區隱藏指標實驗結果。

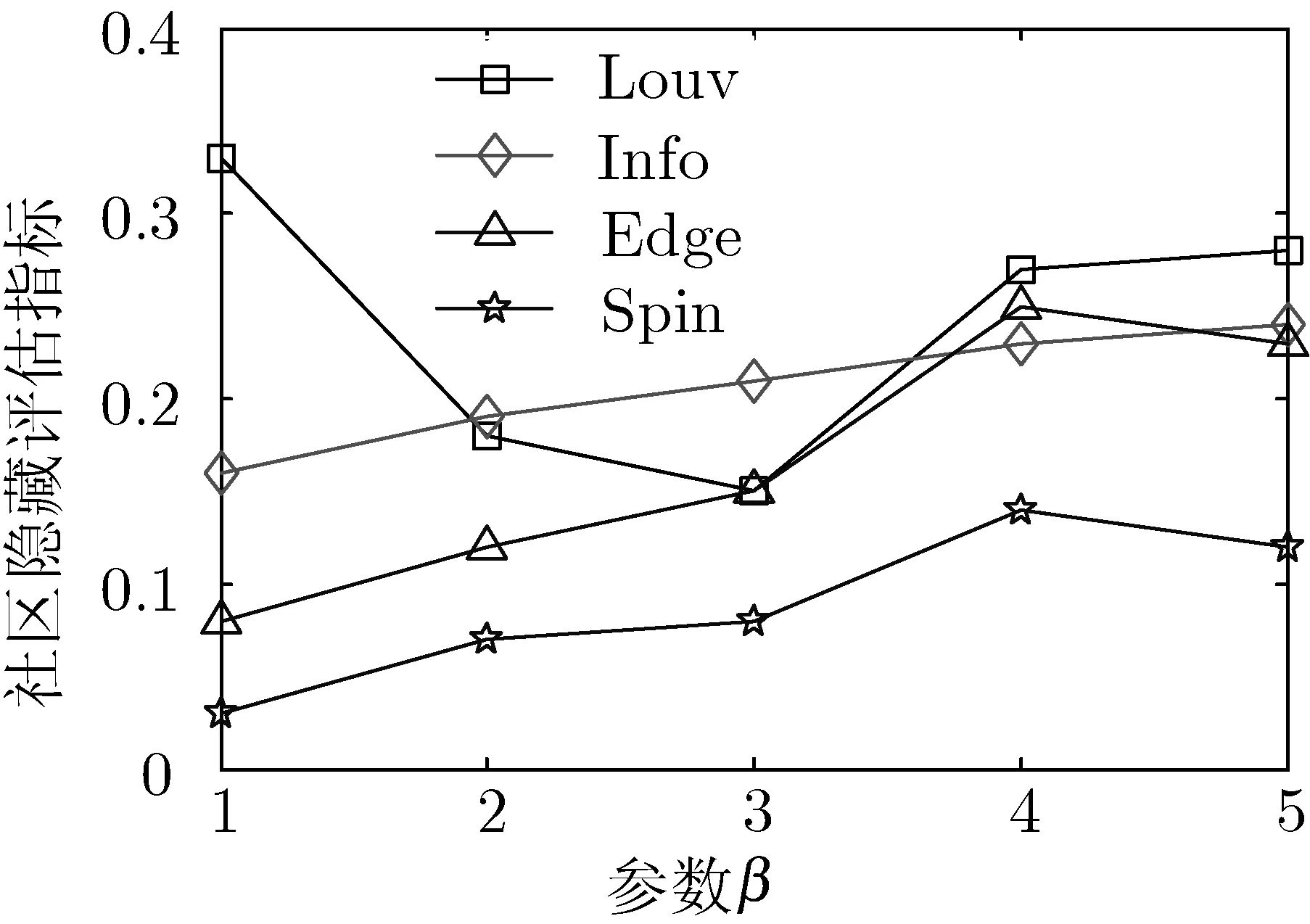
(a) kar網絡實驗結果

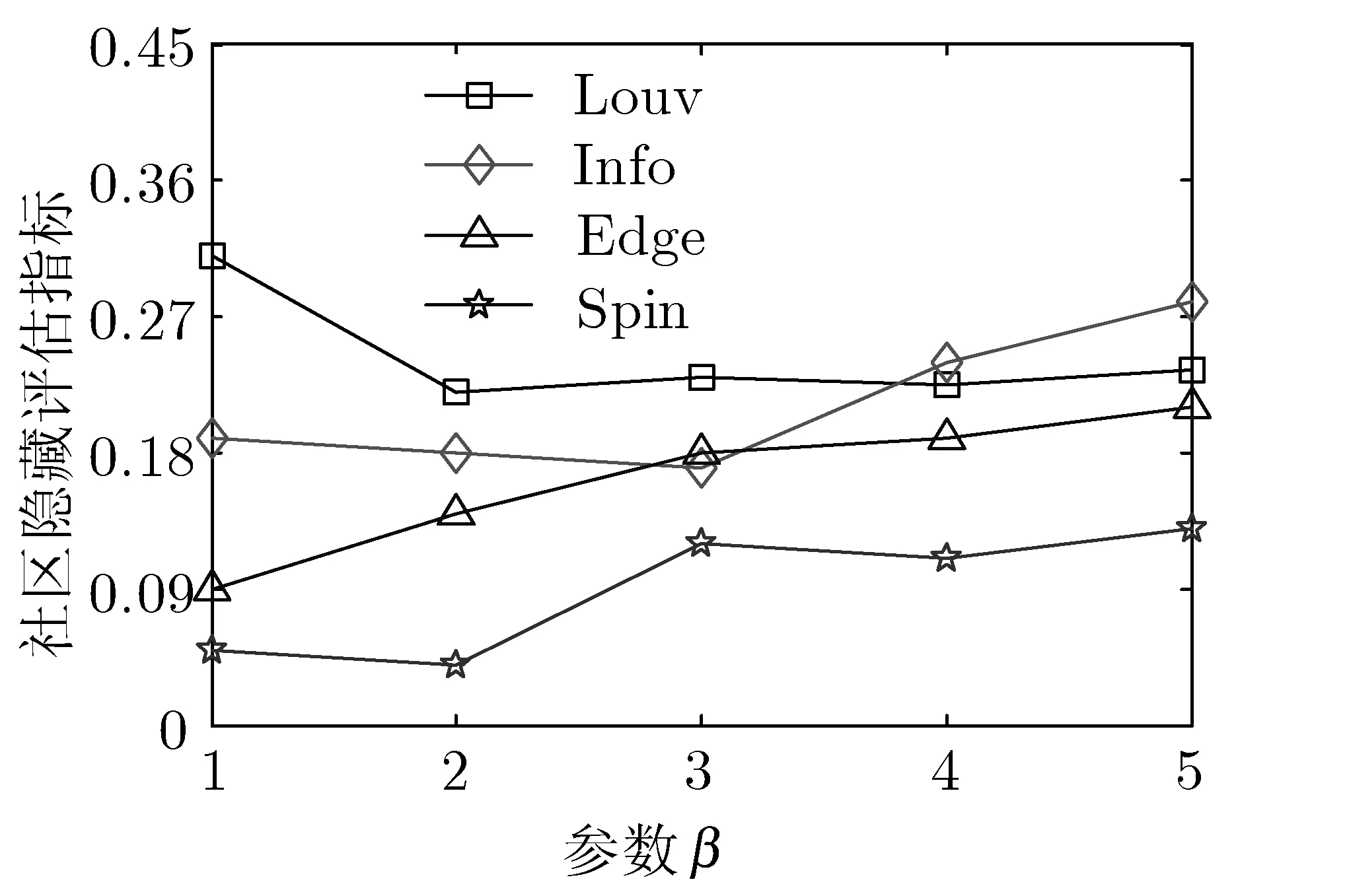
(b) dol網絡實驗結果

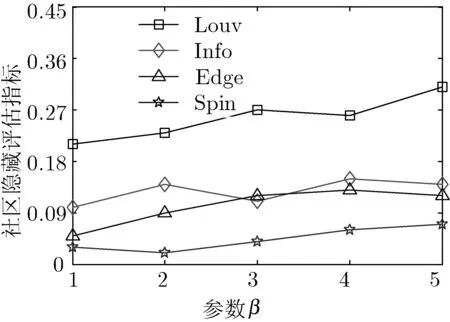
(c) polb網絡實驗結果

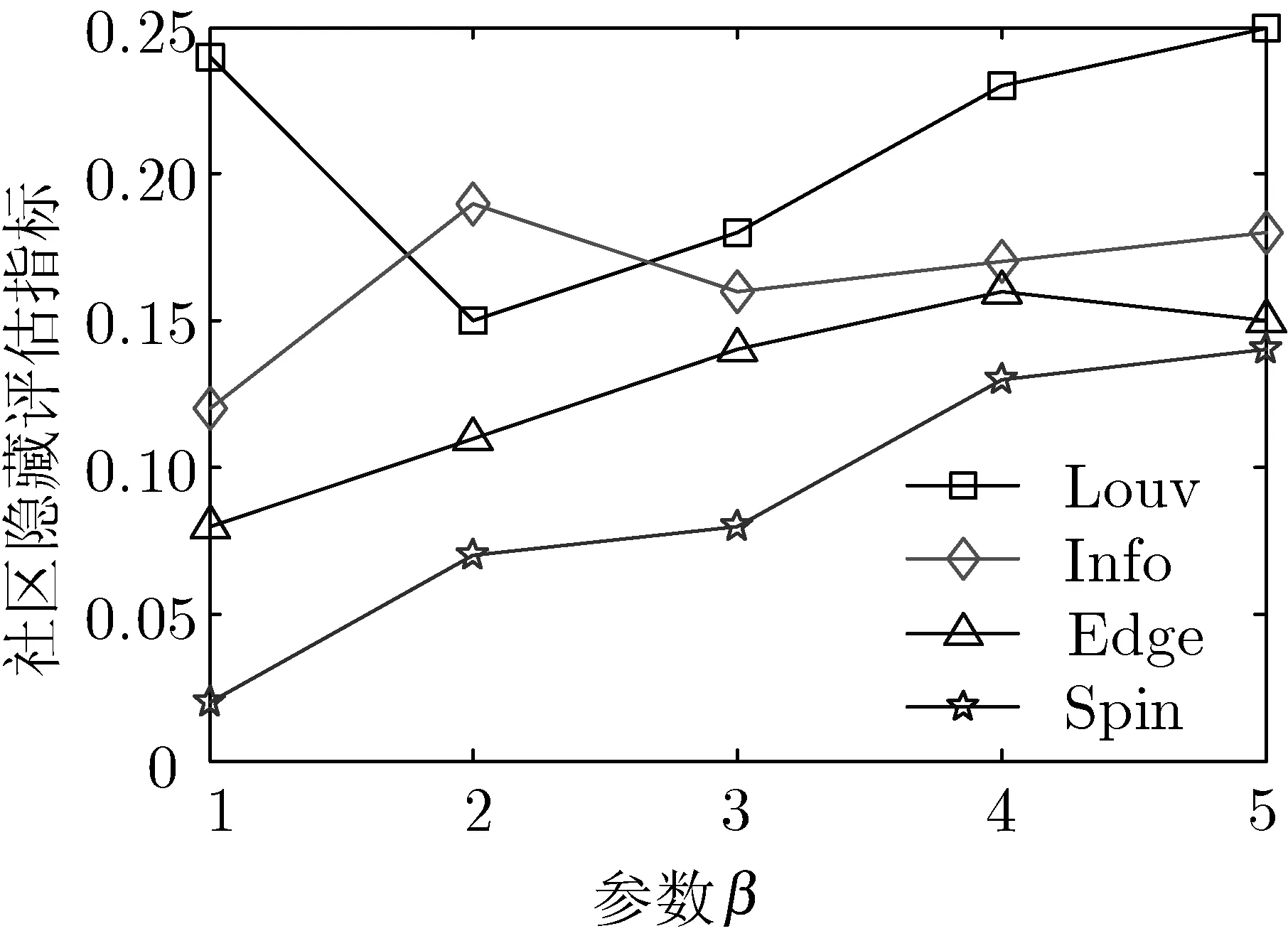
(d) mad網絡實驗結果圖3 網絡隱藏指標

根據圖3所示網絡隱藏指標實驗結果可知，隨著參數β的增大，幾種算法在4種網絡上的實驗結果均呈現出增大的趨勢。同時，可看出個別情形下呈現出波動性，對這樣的行為可解釋為：這些算法不是基于模塊最大化的，算法產生一個更新網絡，具有較低的模塊化價值不會帶來足夠的中斷INF的功能，產生更大的評估價值[15]。

此外，為更加直接地驗證所提算法的社區隱藏性能，這里選取參數β取值為1～5，驗證算法在kar、dol、mad、polb 4種實驗網絡上，更新前、更新后以及隨機節點邊緣調整方式的特定社區檢測概率。該結果為每種算法運行30次的均值結果，見表3。

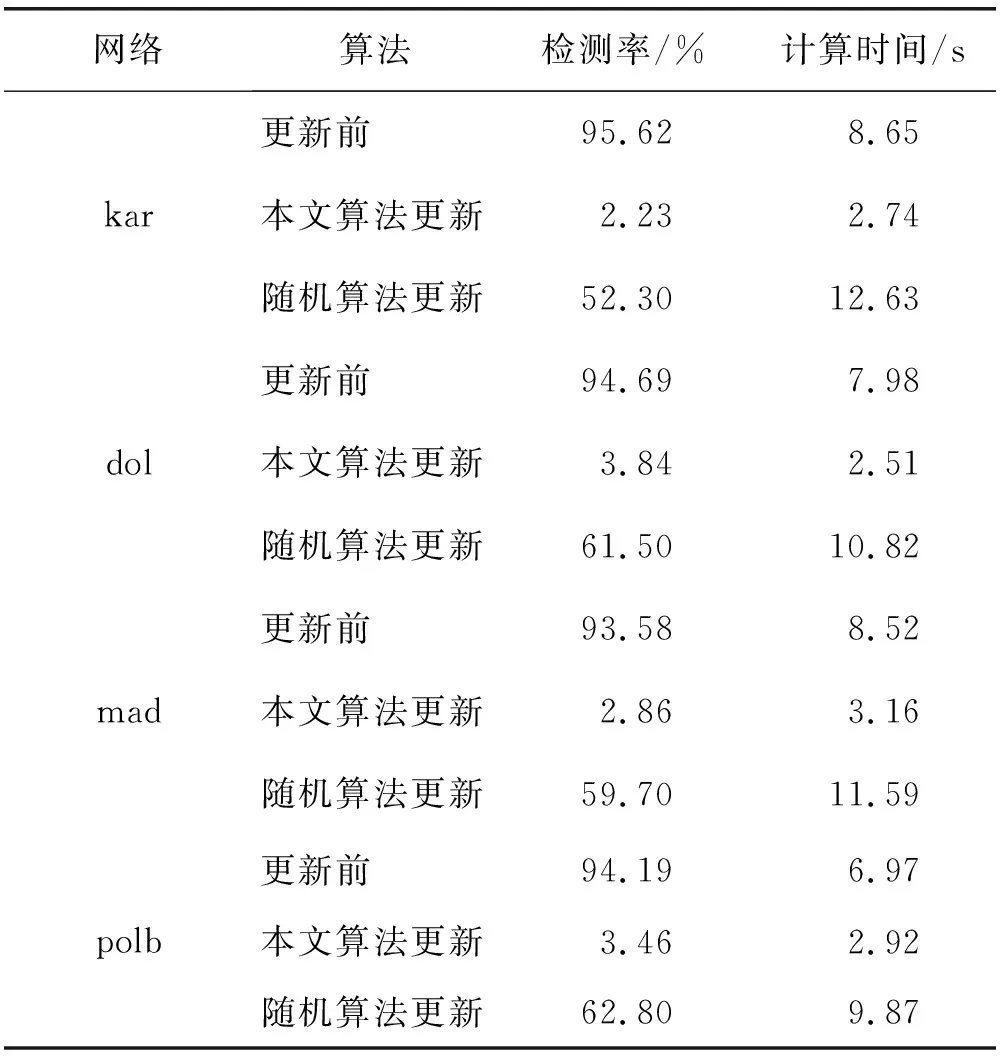
表3 特定社區的隱藏性能

表3所選取的特定社區選取標準是根據上述實驗數據網絡的真實社區劃分結果選擇的。其中本文方法和隨機調整方式的節點和邊緣更新數量均設定為5。根據表3實驗結果可知，在特定隱藏社區的檢測概率上，本文算法更新后的網絡始終保持在較低的水平上，在3%左右。而更新前網絡特定隱藏社區的隱藏性能相對較差，都達到了90%以上，隨機更新策略的社區檢測率也達到了50%以上，這體現出所提算法較高的社區隱藏能力。在算法的執行時間指標上，本文算法更新后的網絡的運行時間2～4 s，而更新前網絡的運行時間相對較長，這表明本文算法具有相對較高的社區隱藏效率，能夠先于社區檢測算法實現對社區的實時隱藏。

5 結 語

本文提出一種考慮內外均衡安全增益的可量化社區隱藏算法，在給出社區網絡模型的基礎上，對社區隱藏的評價指標進行定義，實現了社區隱藏的量化分析。然后基于社區檢測的安全性增益指標對社區隱藏過程中的節點添加和邊緣的刪除策略進行研究。基于這些操作實現對網絡社區的更新，最后對社區檢測隱藏算法的安全性進行了理論分析，為社區隱藏算法應用提供理論基礎。本文研究目的并不是如何獲得更佳的社區隱藏性能，而是通過研究社區隱藏過程，探索其存在的共性因素，從而對社區檢測算法起到更多的指導意義。下一步的研究重點是：探索自然網絡中存在的有意或者無意的社區隱藏行為，分析其存在的物理意義，并有針對性的實現檢測突破，這對于提升社區檢測算法性能具有重要的意義。