激光掃描匹配方法研究綜述

宗文鵬，李廣云，李明磊，王 力，李帥鑫

(信息工程大學，河南 鄭州 450001)

1 引 言

定位是移動機器人領域研究最多也是最核心的問題之一，是機器人實現真正自主的先決條件，沒有準確高效的定位，機器人就難以執行復雜的任務。通常，移動機器人可通過輪式里程計、慣性導航裝置(Inertial Measurement Unit,IMU)等本體傳感器進行定位。然而由于車輪打滑和漂移導致誤差累積問題，故單獨依靠本體傳感器并不能提供準確可靠的定位結果。因此，移動機器人一般還需要加裝外部感受傳感器，如聲吶、超聲傳感器、視覺傳感器、激光雷達(Light Detection and Ranging,LiDAR)等。在進行定位的同時，利用這些傳感器采集信息，能夠建立環境的抽象表示即地圖，地圖反過來又輔助機器人進行定位，這是移動機器人實現避障、路徑規劃、目標識別與跟蹤等任務的必要基礎。于是，同步定位與地圖構建(Simultaneous Localization and Mapping,SLAM)[1]技術應運而生。目前，最熱門的SLAM實現方案主要依賴兩類傳感器，即激光雷達和視覺傳感器，它們分別被稱為激光SLAM和視覺SLAM[2]。相對于視覺傳感器，LiDAR能夠提供更加魯棒、準確和噪聲水平穩定的測量信息，且對光照條件變化不敏感，因而激光SLAM是目前最穩定可靠的SLAM解決方案。

根據求解方法不同，可將激光SLAM分為基于濾波的和基于圖優化的兩種[3]。其中，當前較為流行的基于圖優化的激光SLAM系統框架主要分為前端和后端兩個部分，前端完成數據關聯和閉環檢測，后端進行圖優化。激光掃描匹配是實現激光SLAM數據關聯最常用的方法。大多數文獻中對激光掃描匹配的定義為，尋求一組平移和旋轉參數，使得對齊后的兩幀掃描點云達到最大重疊[4-6]。本文嘗試給出一個更一般的定義，即通過求解坐標轉換關系，將連續掃描的兩幀或多幀激光點云統一到同一坐標系中(scan-to-scan)，或者將當前掃描點云與已建立的地圖進行配準(scan-to-map)，從而最終恢復出載體位置和姿態的變化。

“掃描匹配”這一概念主要出現在機器人學相關文獻中，本質上它與測繪等領域中的“點云拼接(或配準)”[7]解決的是同一個問題，但目的不同：前者通過將激光掃描點云配準到同一坐標系下而得到相對位姿變化，后者是為得到坐標系統一的點云。此外，由于應用場合和針對的目標不同，掃描匹配和點云拼接各有其特點。激光掃描匹配處理的是移動載體運動時LiDAR的掃描數據，點云較稀疏，且誤差和噪聲均較大，大多要求實時處理，力求在精度和效率之間尋求平衡；而點云拼接處理的多是LiDAR靜態掃描數據，點云較密集，且誤差和噪聲較小，一般不要求實時處理而更注重拼接的精度。

近年來，激光SLAM技術發展迅猛，其應用從結構化場景拓展到非結構化場景，從室內環境發展到室外環境，從地面移動平臺擴展到空中以及水下。相應地，激光掃描匹配技術經歷了2D到3D、低動態到高動態、簡單場景到復雜環境的發展變化，除用于激光SLAM外，也越來越多地被應用于導航定位[6,8]、移動測量[9]等領域。根據所處理的LiDAR數據的維度，掃描匹配可分為2D和3D掃描匹配。根據是否利用特征，掃描匹配可分為基于特征的和基于掃描的兩種[10]。根據匹配時的參考對象，又可分為局部和全局掃描匹配[11]。一般來說，局部掃描匹配處理對象為連續獲取的兩幀掃描數據，通常需要利用里程計或IMU的輸出或前一次掃描匹配結果作為初值，主要用于位姿跟蹤，實現相對定位；而全局掃描匹配[12]將當前幀掃描數據與全局地圖或過往全部掃描數據幀進行匹配，無需初值，用于實現全局定位。本文沿用文獻[13]和[14]的分類方法，將激光掃描匹配分為三類：(1)基于點的掃描匹配；(2)基于特征的掃描匹配；(3)基于數學特性的掃描匹配。

需要指出的是，本文主要側重于連續掃描幀間匹配(scan-to-scan)問題，對激光掃描匹配相關方法按照上述三種類型進行總結和討論，旨在幫助讀者快速了解該方向現有研究方法和存在的問題，以便在此基礎上開展相應的研究。

2 基于點的方法

基于點的掃描匹配直接對掃描獲取的原始數據點進行操作，其中ICP (Iterative Closest/Corresponding Point)算法是應用最廣、研究最多也是目前最為成熟的一種算法。ICP分別由Chen[15]和Besl[16]獨立提出。不同之處在于前者利用點到面的距離作為誤差度量，而后者采用點到點的距離誤差度量，故可分別記為P2Pl(Point-to-Plane)-ICP和P2P(Point-to-Point)-ICP。

2.1 標準ICP算法

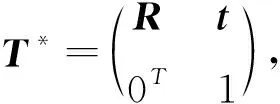
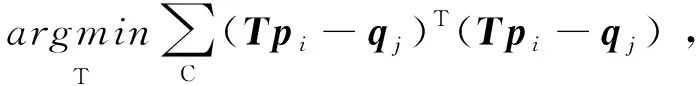
其中，R∈SO(3)為旋轉矩陣，t為平移向量，eij為誤差度量，C={(i,j)m}表示對應點對集合，點pi對應點qj。

2.2 ICP的改進算法

Besl[16]證明了ICP算法總能單調收斂到一個局部最小值，但這基于一個假設，即對應點對數量及對應關系在迭代過程中保持不變，而這顯然是不現實的。此外，ICP算法還假定兩個點云中的點完全相同，而事實上，當傳感器視點改變后，尤其是當采樣分辨率較低時，前后兩次掃描找到同一物理點的對應點對的可能性極小。為此，Chen[15]提出P2Pl-ICP算法，采用更魯棒的點到面的距離作為誤差度量替代點到點距離誤差度量，即：

eij=(Tpi-qj)·nj, (2)

其中，nj為點qj處的法向。

標準ICP算法所采用的歐式距離，不能很好的解釋傳感器的旋轉變化，當目標函數接近局部極值時收斂很慢。文獻[17]提出計算兩組對應關系，一組采用歐氏距離，另一組利用極坐標距離和角度，聯合兩種對應關系準則，提出了IDC(Iterative Dual Correspondence) 算法。該算法改善了ICP算法對于傳感器旋轉角度的表達，加快了收斂速度，但同時采用兩種對應關系建立準則分別求解平移和旋轉，可能出現多組極值組合，從而影響算法的魯棒性和精度。文獻[18]提出一種組合掃描匹配方法CSM(Combined Scan Matcher)，聯合了一種點-線掃描匹配方法[19]和一種點-點掃描匹配方法[17]；當掃描數據中存在足夠多的直線用于匹配時執行點-線掃描匹配算法，否則執行點-點掃描匹配算法。

文獻[20]提出的MbICP(Metric-based ICP)算法，定義了一種傳感器位形空間中新的距離度量，同時考慮平移和旋轉，使得平移和旋轉在所有步驟中同時得到補償，改善了算法的魯棒性、精度、收斂性，并降低了計算代價。MbICP能夠處理較大的旋轉，但該方法不能利用KD樹等技術來加速最近鄰域搜索，需要在極坐標空間進行較慢的搜索，難以擴展到完全3D的掃描匹配[21]。

針對此問題，文獻[11]引入了一種除幾何關系外的新的度量，即點云強度信息，提出了“Intensity-ICP”方法。該方法將強度誤差度量納入到目標函數中，并賦以通過實驗確定的權重。該方法為相對位姿的求解增加了一個新的約束，為解決具有相同幾何形狀而不同反射特性的場景下的掃描匹配提供了可能。但該方法基于前后兩次掃描間距離變化足夠小而不影響強度的假設，而實際上強度值受測量距離和入射角的影響均較大，應用前需先對傳感器的強度測量進行標定；存在的另外一個問題是難以準確度量強度誤差對位姿變化的貢獻，即難以確定一個合適的權重值。

文獻[22]和[23]提出ICL(Iterative Closest Line)算法，即利用點-線距離度量來實現ICP，以提高精度和收斂速度。但是對于較大的位移穩定性較差。文獻[24]采用3D柵格，將點云分割成體素(Voxel)[25]，以體素對應關系代替了傳統ICP中的點間對應關系，且考慮了點云局部結構即體素的形狀參數，實現了3D掃描匹配，能夠用于室內外結構與非結構化場景中，得到局部一致的測圖結果。

文獻[26]提出GICP(Generalized-ICP)算法，在單個概率框架中結合了P2P-ICP算法與P2Pl-ICP算法，誤差度量中既包含當前掃描也包含了參考掃描的表面信息，所采用的誤差度量可視為面到面距離，從而GICP是一種Pl2Pl(Plane-to-Plane)-ICP算法。GICP核心思想是考慮點周圍的表面形狀，并近似為平面片，利用了點云表面局部連續這一性質，考慮進了傳感器的噪聲模型，利用法向來給目標函數中的每個對應匹配賦權，能有效降低誤匹配的影響，已成為眾多ICP改進算法中最為有效和魯棒的算法之一。但需要指出的是，在室外及非結構化場景中GICP并不比標準ICP表現出色[35]。文獻[27]和[28]拓展了GICP中提出的面-面誤差度量，在求解最優變換時，最小化的誤差度量為各對應點對的馬氏距離及它們的法向。該算法的主要特點為：對每個點，考慮其周圍表面特性，計算法向和曲率；在尋找對應關系和最優變換求解中都利用了場景結構，采用了測量的擴展表示，即每個點的歐式坐標用表面法向增廣，誤差度量是6D向量而不再是3D點。

文獻[29]提出一種ICP預處理技術ICN(Iterative Closest Normal)，其目的是估計連續掃描幀間大的旋轉，當處理了大的旋轉后再采用標準的ICP或點-線ICP來估計剩余變換。為避免ICP算法局部最優問題，文獻[30]提出Go-ICP方法，將ICP算法與分支定界方法相結合，以保證求解的全局最優，但計算代價較大；文獻[31]將基于八叉樹的ICP算法與分層搜索策略相結合，利用一種早期預警機制來監測局部極小問題，并采用一種啟發式逃離方法來避免局部極值從而獲得全局最優解。

傳統的ICP改進算法通常假設獲取一幀掃描數據的時間足夠短，從而近似認為所有掃描點是同時測得的，但實際上掃描數據是依次測量得到的，而在這一過程中，傳感器的位姿始終在變化，獲得的點云存在變形，因而當傳感器運動速度較快時，傳統的ICP改進算法會給出錯誤的位姿估計。文獻[32]指出在確定對應點前需要對掃描數據進行畸變改正，提出一種利用速度更新增強ICP算法的新方法VICP(Velocity updating ICP)，在ICP的迭代求解過程中估計傳感器速度，利用該速度估計來補償由于運動造成的點云畸變；并且，在速度更新的迭代過程中，能夠有效排除異常點，從而得到更加魯棒和準確的位姿估計。文獻[33]中Continuous-ICP(CICP)將ICP算法進一步擴展，提出一種用于特定類型3D LiDAR(由2D LiDAR+旋轉驅動裝置組成)-SLAM的連續時間軌跡估計方法，利用估計的連續位姿進行畸變改正。

2.3 模塊化的ICP算法

隨著ICP及其改進算法的不斷發展和完善， ICP類算法可歸納為以下6個步驟[34]：

(1)選擇點集；

(2)確定點集間對應關系；

(3)給對應點對適當加權；

(4)排除特定的對應點對；

(5)設定誤差度量；

(6)最小化誤差度量。

Pomerleau[35]通過分析概括已有ICP改進算法并結合自身開發經驗，提出了模塊化的ICP算法，既方便進一步開發和調試新算法，同時又便于對不同改進算法進行對比。如圖1所示，首先，可先對輸入掃描點云進行濾波處理，去除冗余點、離群點，或計算表面特征如曲率和法向；然后，將匹配函數用于關聯輸入點云和參考點云的元素，通常這一關聯過程在歐式空間進行并利用KD樹加速搜索；建立好元素對應關系后，可利用不同的統計方法來排除錯誤或異常的元素對應，如可設置距離閾值，超過該閾值的對應點對被認為是無效對應而被剔除；最終，剩余的有效對應元素對被用于最小化誤差度量，求解新的變換關系直到滿足收斂條件。

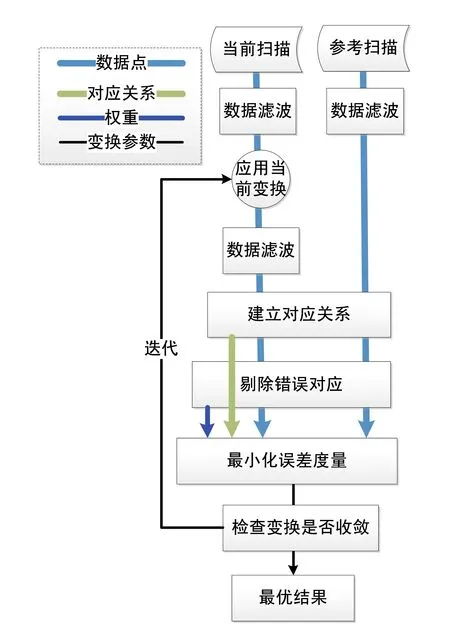
圖1 模塊化ICP算法流程圖 Fig.1 Pipeline of modular ICP

2.4 其他基于點的方法

除了ICP及其改進算法外，還存在其他一些基于點的掃描匹配方法。文獻[37]提出一種概率的掃描匹配方法pIC(probabilistic Iterative Correspondence)。其將掃描點及位姿視為隨機變量，利用馬氏距離尋找所有可能的統計相容點(即對應點)，概率模型納入了傳感器測量噪聲及初始位姿的不確定度，利用迭代的方式進行求解，收斂速度、魯棒性和精度優于標準ICP和IDC算法。Diosi提出極坐標掃描匹配方法PSM(Polar Scan Matching)[38]，使得對應點匹配更加準確可靠，從而提高了掃描匹配效果。后來他又提出改進的掃描匹配方法[39]，利用LiDAR測量為極坐標的本質，直接利用極坐標量即距離和角度測量值，結合匹配關聯規則和加權距離殘差最小化來實現掃描匹配，提高了處理速度并擴大了收斂域，但該方法難以擴展到3D掃描匹配。文獻[40]提出一種改進的PSM方法，利用遺傳算法來進行匹配，避免了ICP類算法中容易出錯的數據關聯步驟。文獻[41]又提出一種基于周界的PSM算法，稱為PB-PSM，獲得了更好的效果。

文獻[42]提出CRSM(Critical Rays Scan Matching)的思想，不需使用所有數據點參與匹配，而是在每幀掃描數據中根據掃描密度尋找關鍵射線對應的測量點，提出了一種基于射線篩選的掃描匹配方法，有效降低了計算復雜度，減少匹配所需時間。文中提出和對比了3種不同的射線篩選方法，均勻篩選方法、基于掃描密度的方法以及將掃描數據分段并利用局部密度的方法。利用隨機重啟爬山法代替遺傳算法進行求解，比ICP算法更準確比遺傳算法更快。其實驗結果得到一個有益的啟示，即利用全部可用信息進行掃描匹配并不總會改善結果。

2.5 存在的主要問題和發展趨勢

ICP類算法存在3個主要誤差來源[43]：

(1)錯誤的收斂，ICP算法總是收斂到局部極值的本質導致最終結果可能偏離真值，該誤差難以建模；

(2)欠約束導致的誤差，一些環境下沒有足夠的信息來估計完整的位姿信息，如長直走廊環境或圓形場景，但可通過Fisher信息矩陣來檢查是否是該情況；

(3)傳感器噪聲引起的誤差，即使ICP算法到達真值的收斂域，傳感器噪聲的存在仍將導致其最終結果不同。當ICP用于定位時，克拉美-羅下界[44]給出了協方差的良好近似，但是對于掃描匹配來說過于樂觀。

此外，由于數據關聯開始是未知的，迭代的方法不一定能建立正確的對應關系。由最小二乘導出的不確定度估計不能準確反映數據關聯中的不確定度，不確定度估計往往過于樂觀[45]。另外兩個與ICP算法相關的問題為：

(1)計算效率問題：為加速收斂，Besl[16]基于最近兩到三次迭代過程中變換變量的值，利用線搜索方法啟發式地確定變換變量；雖然這在一定程度上改善了局部極值處的收斂速度，但對于較大的旋轉仍然不能得到較好的結果。尋找對應點的過程計算復雜度相當高，加速搜索過程需利用KD樹[46]或最近點高速緩存[47]等技術。

(2)魯棒性問題：異常點對掃描匹配影響較大，文獻[20,39]等提出采用預處理技術減少異常點。盡管如此，很難將LiDAR數據中所有異常點或噪聲徹底剔除。

ICP類算法已從最初的迭代最近點發展到迭代對應點再到迭代對應元素，在魯棒性、計算效率和收斂域方面得到了提高。未來，將有更多的可用信息被利用，從而進一步改進ICP算法，如強度信息、語義信息；對應元素可進一步拓展到體素及超體素[48]，將有更多的非線性優化算法能夠用于參數求解。

3 基于特征的方法

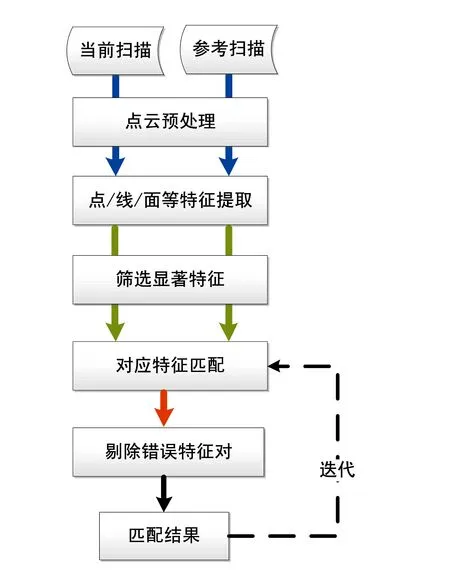
圖2 基于特征的掃描匹配方法流程圖 Fig.2 Pipeline of the feature-based scan matching method

與其利用可能包含異常點和噪聲的所有LiDAR數據，激光掃描匹配的另外一種思路是只利用數據中的部分關鍵元素進行匹配，這種元素可以是點、線、面等幾何基元或者它們的組合。于是催生了另一個系列的激光掃描匹配方法，即基于特征的掃描匹配，其流程如圖2所示。基于特征的掃描匹配方法，類似于圖像匹配問題，需要先從掃描點云中提取有效特征，如點、線、弧、面或其組合特征，以及法向、曲率等柔性特征，還包括自定義的各種特征描述子。基于檢測到的特征，可實現快速對應匹配，無需提供初值，即可求解位姿變化。

3.1 直接從LiDAR點云中提取特征

(1)點特征

點特征廣泛存在于各種場景中，基于點特征的掃描匹配方法應用較廣，適用性較強。文獻[49]直接從點云中提取拐角和邊角點，用于全局掃描匹配。受計算機視覺中SIFT特征描述子的啟發，文獻[50]提出一種用于2D掃描匹配的局部不變特征CIF(Congruence Transformation Invariant Feature)，當應用全等變換時保持不變；利用從LiDAR數據中提取的CIF特征點，可實現雜亂環境下的全局掃描匹配。文獻[51]又對CIF方法進行了改進，解決當利用較大地圖作為參考掃描進行掃描匹配時容易失敗的問題。文獻[52]提出ICE掃描匹配方法，利用多種特征點，包括交叉點(Intersection)、角點(Corner)和墻的端點(End Of Wall)。

文獻[53]提出一種自動化、實時的基于角點的掃描匹配算法，以提取的線之間的交叉點作為角點；為說明角點的不確定度，利用提取線的方差來估計角點的協方差；該算法既可單獨使用，也可用于輔助迭代方法。文獻[54]提出一種叫做FLIRT的方法，研究了3種類型的激光點云特征檢測子(基于距離、法向和曲率)和兩種特征描述子(線性局部形狀上下文描述子和β-柵格描述子)。基于綜合分析，進行最佳組合形成FLIRT，但是計算其描述子非常慢，難以用于實時SLAM。事實上，3D激光點云的點特征檢測方法和特征描述子[55-56]還有很多，但大多由于提取精度、計算效率、適用條件等問題難以用于激光掃描匹配。

(2)線特征

在室內及結構化場景中，存在較多的線特征，特別是對于2D掃描匹配方法，線特征的提取(即分割)較為簡單和高效，因而基于線特征的掃描匹配方法主要存在于2D應用中。分割-合并(Split-and-Merge)方法[57]是2D掃描匹配中廣泛采用的一種線段分割方法，此外，文獻[58]給出了針對2D掃描數據的3種線段分割方法，即連續邊緣跟隨(Successive Edge Following,SEF),線跟蹤(Line Tracking,LT), 迭代端點擬合(Iterative End Point Fit,IEPF)。霍夫變換也是提取線特征的一種有效方法[59]，文獻[60]提出HSM(Hough Scan Matching)方法，利用霍夫變換提取線段，并在霍夫域進行匹配，但當環境中包含大量較短線段或曲線時，這種方法不再適用。

文獻[61]提出基于完整線段(Complete Line Segment, CLS)的掃描匹配方法，根據線段長度、中心點的相對位置、相對旋轉進行線的對比。文獻[62]利用互兼容約束來實現線段關聯，從而實現掃描匹配。文獻[63]利用曲率方法，通過自適應曲率函數將掃描點云分為曲線段和直線段。文獻[64]提出的2D掃描匹配方法，首先利用模糊聚類算法分割點云，然后對每段進行加權最小二乘擬合，選擇兩幀掃描數據中滿足線性分布的線段進行匹配，從而計算旋轉參數，然后再利用點匹配準則對點建立對應關系，從而求解平移參數。文獻[65]提出一種基于點和線特征的2D掃描匹配方法，基于擴展的1D SIFT檢測顯著特征點，利用改進的分割-合并算法提取線特征，利用距離直方圖來描述點和線特征，采用直方圖聚類技術濾除異常對應，從而提供準確的剛體變換的初始值；相對位姿估計采用lq范數度量，而不是經典優化方法中代價函數所采用的l2范數。

(3)面特征

室內及城市環境中，存在大量的平面或曲面特征，合理利用這些特征同樣能夠實現激光掃描匹配。文獻[66]從掃描數據中提取歐式不變特征，利用幾何哈希法匹配兩幀掃描數據，需要場景中包含曲面形狀物體。文獻[67]利用體素濾波器對原始數據進行均勻下采樣，通過區域生長提取平面宏特征，如墻面和大平面，只利用平面上的點進行掃描匹配，剔除了人及其他不相關特征即雜亂點。文獻[68]提出了一種從稀疏點云中高效提取線和面特征的方法。文獻[69]提出的Loam(Lidar odometry and mapping)算法中，使用位于銳利邊緣線和平面上的特征點，并且分別匹配特征點到邊緣線段和平面片上，通過掃描匹配實現LiDAR里程計，對不同類型的3D LiDAR，在多種場景中均取得了出色的效果。

(4)其他特征

其他基于特征的掃描匹配方法使用點特征直方圖PFH(Point Feature Histograms)[70]及其更快的變種FPFH(Fast Point Feature Histograms)[71]、角度不變特征[72]、曲率函數[73]等。此外，文獻[74]利用城市環境中存在大量垂直表面，如建筑物墻面、甚至垂直樹干等，實現掃描匹配。文獻[75]提出一種分類特征掃描匹配方法CFSM (Classified Feature-based Scan Matcher)：根據幾何觀測，將特征分為平移特征和旋轉特征兩類，分別用于解釋傳感器的平移和旋轉變化，并利用解析式計算位姿估計。文獻[76]提出一種利用條件隨機場(Conditional Random Fields,CRF)的基于特征的方法：采用一幀掃描中的所有觀測進行聯合估計，考慮形狀信息進行誤匹配剔除；該模型能夠組合多種特征，如形狀特征和外貌特征；但計算復雜度較高，且對于部分重疊的幀間掃描匹配不可靠。文獻[77]提出利用方向分布表征掃描點云的幾何趨勢，從而通過巴氏距離度量兩幀掃描數據間的相似度。該方法能夠給出兩幀掃描數據間旋轉變化的初始估計，因而能夠處理大的旋轉變化。

3.2 轉換為圖像并提取特征

相較于直接處理散亂的無序點云數據，將掃描數據轉化為圖像并利用相對成熟的圖像處理方法來實現激光掃描匹配是另一種切實可行的思路。文獻[78]將點云投影為圖像，然后提取SIFT特征；文獻[79]通過點云生成深度圖像然后提取NARF(Normal Aligned Radial Feature)特征用于匹配。文獻[80]考慮掃描匹配效率和數據存儲問題，提出利用多分辨率影像金字塔來處理一對多，多對多2D掃描匹配問題。文獻[81]提出一種基于關鍵點的2D掃描匹配方法，該方法首先將LiDAR數據轉化為占據柵格地圖，然后再轉換到圖像，利用Harris角點檢測方法來提取關鍵點，最終利用RANSAC(Random Sample Consensus)算法實現匹配。文獻[82]利用從360°點云中提取的面片進行掃描匹配，為加快點云處理，將點云投影到3個2D圖像來提取面片。

3.3 存在的主要問題和發展趨勢

在結構化場景中，基于特征的掃描匹配方法能夠處理具有部分重疊和較大偏移的連續掃描，但也存在一些問題：

(1)對于稀疏的掃描點云或非結構化場景，難以提取穩定可靠的特征，而對于特征豐富場景，匹配時存在歧義或模糊問題；

(2)提取魯棒的特征需要較高的計算代價，計算特征描述子需花費大量時間；

(3)缺乏適當的策略來移除誤匹配特征，而一旦存在誤匹配的特征，將會導致重大錯誤而不僅是誤差的增大；

(4)相比于ICP類算法，通常精度較差，因而對于通過增量式的連續掃描匹配來估計位姿，往往會存在更為嚴重的漂移。

鑒于上述問題，采用由粗到精的混合掃描匹配方法逐漸成為一種趨勢，先用基于特征的方法求得初始位姿估計，再運行ICP類算法進一步修正位姿，從而最終得到準確的位姿。如文獻[14]和[83]所用掃描匹配方法默認工作在基于特征的掃描匹配模式，當沒有足夠線特征可匹配時，激活ICP掃描匹配模式。此外，文獻[84]提出了一種新穎的3D特征，能夠從存在運動畸變的點云中魯棒地提取出來并匹配，為實現不進行畸變改正直接對變形的連續掃描點云進行掃描匹配提供了可能。

4 基于數學特性的方法

除了基于點的掃描匹配和基于特征的掃描匹配，還有一大類利用各種數學性質來刻畫掃描數據及幀間位姿變化的掃描匹配方法，其中最著名的當屬基于正態分布變換(Normal Distributions Transform,NDT)的方法。

4.1 NDT及其改進算法

點云是激光掃描數據最簡單直觀的表達形式，對于可視化來說非常有用，但是點坐標的表示形式不能明確表達被測目標的表面特性，如表面朝向、平滑度、孔洞等。因此，Biber[85]提出一種基于NDT的2D掃描匹配新方法，成功用于相對位姿跟蹤和激光SLAM。該方法將單次掃描中的離散2D點變換為定義在2D平面上的分段連續且可微的概率密度，概率密度由一組容易計算的正態分布構成，另一幀掃描與NDT的匹配就定義為最大化其掃描點配準后在此密度上的得分，并利用牛頓法進行優化求解。該方法的顯著優點是，不需要建立點間或特征間的明確對應關系，而對應關系確立過程往往存在錯誤關聯，因而更魯棒；正態分布給出了掃描數據的分段光滑表示，具有連續的一二階導數，有了該表示，使得將標準的數值優化方法應用于掃描匹配成為可能，導數可解析計算，從而求解更快速和準確。

文獻[86]將2D的NDT方法推廣到3D，提出一種P2D(Point-to-Distribution)-NDT掃描匹配方法。該算法首先將參考幀掃描數據劃分為小立方體(體素)組成的網格，對于每個體素利用其內部包含的點qk=1,…,m計算一個概率密度函數(Probability Density Function,PDF)，每個體素內的PDF可以視為表面點x的生成過程，即點x是根據PDF表示的分布采樣得到的。假設服從D維正態分布，則在測得點x的似然為:

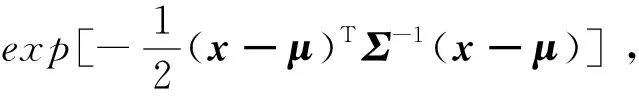
其中，μ和Σ表示體素內點的均值向量和協方差矩陣，即:

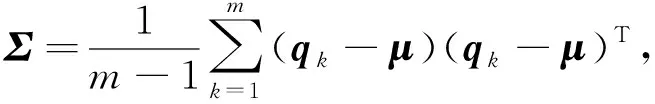
應用NDT進行掃描匹配的目標是尋求位姿變換T，使得變換后當前幀掃描中的點位于參考幀掃描表面的似然最大，即

這里的PDF不必限定為正態分布，可以選用任意能夠恰當表示表面結構且對異常點魯棒的分布。由于單純的正態分布對異常點不魯棒[87]，NDT算法中采用的PDF是正態分布和均勻分布的混合，即

Σ-1(x-μ)]+c2ξ0, (7)

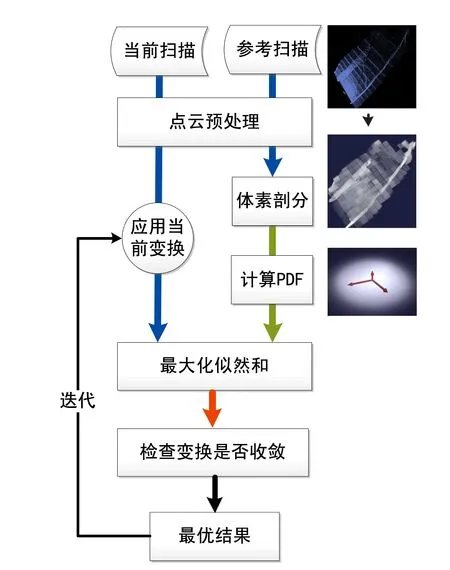
圖3 P2D-NDT掃描匹配方法流程圖 Fig.3 Pipeline of the P2D-NDT based scan matching method

文獻[89]將P2D-NDT進一步擴展，對待匹配的兩幀掃描數據均用正態分布表示，提出D2D(Distribution-to-Distribution)-NDT方法，并且討論了迭代優化算法初始點的選取以及協方差的估計。由于D2D-NDT方法只在NDT模型上進行操作，其運行速度比P2D-NDT要快得多，但代價是魯棒性稍差[90]。此外，NDT還存在多種改進算法，這里不再一一列舉。

4.2 其他方法

基于相關或互相關的掃描匹配方法研究相對較多。文獻[91]提出的CCF方法將2D掃描數據轉換為統計表示形式，利用角度直方圖以及x、y直方圖間的歸一化互相關來實現匹配。文獻[92]提出一種新的魯棒的互相關掃描匹配方法，對于大的平移和旋轉也能較好處理，且對環境中的動態目標魯棒。基于互相關的方法雖然效率高得多，但精度低于ICP算法，適用于載體計算能力有限的平臺。

文獻[4]提出利用廣義霍夫變換(Generalized Hough Transform,GHT)得到的粒子分布來近似目標分布，稱為GPM(GHT Particles Matching)，該方法能夠應用于非結構化場景，對遮擋魯棒，在欠約束條件下也能表現良好，執行效率很高。文獻[5]和[8]基于計算機視覺中常用的譜技術[93]提出了譜掃描匹配(Spectral Scan Matching,SSM)方法。該方法包括兩個步驟：首先，利用譜技術及掃描點間的成對幾何關系來確定幾何一致的對應；然后，基于RANSAC的最小二乘擬合用于位姿變化。該方法無需初始對準，甚至能夠用于存在動態目標的場景或掃描點云部分損壞的情況下。

傅里葉梅林變換(Fourier-Mellin Transform,FMT)是廣泛用于圖像配準領域的一種技術，具有良好的抗噪性，不需要特征提取，但計算代價較高。文獻[94]設計了3個1D匹配向量來描述旋轉和平移狀態，將3D問題轉換為1D問題。1D傅里葉變換對于3個不同掃描片段執行3次，顯著降低了計算代價，成功用于2D激光掃描匹配。文獻[95]提出一種基于普魯克分析的2D掃描匹配方法。文獻[96]提出一種基于動態似然場(Dynamic Likelihood Field,DLF)的2D掃描匹配算法，作為非線性最小二乘問題，利用高斯牛頓法求解，避免了需要建立明確的數據對應問題。該方法在保證一定精度的同時在計算效率上具有明顯的優勢。文獻[97]提出一種基于高斯場(類似于NDT中的正態分布)的3D配準準則，該方法的主要思想是采用高斯混合模型同時度量來自兩幀掃描的點間的空間距離和點周圍的局部表面相似性，在由空間維度和許多屬性維度組成的多維空間中比較點。此外，遺傳算法[98]、差分進化算法[99]等元啟發式優化算法也被運用到掃描匹配中。

4.3 存在的主要問題和發展趨勢

NDT類方法比ICP類算法有更高的效率和更廣的收斂域，對于2D和3D應用已有較為成熟的解決方案，但在缺乏良好初值的情況下，也會陷入局部最優。其他基于數學特性的掃描匹配方法目前仍處于初步探索階段，大多只適用于2D掃描匹配，而且難以在匹配過程中給出其結果的不確定度。但隨著激光掃描匹配基礎理論的不斷發展，將有更多的理論方法引入到掃描匹配中，已有的基于數學性質的2D方法將進一步拓展到3D，對相應方法的可觀測性、收斂性及不確定度的研究將進一步發展。

5 激光掃描匹配方法比較與評價

根據前述分析，我們可將典型激光掃描匹配方法的特點總結如表1所示。

表1 典型掃描匹配方法的特點

但激光掃描匹配方法的精度往往難以科學評定，因為難以獲得準確的基準值，并且，掃描匹配受眾多因素的影響：

(1)LiDAR有關的因素，如測量噪聲、頻率、測量范圍及視場大小；

(2)與載體有關的因素，如運動速度(包括旋轉和平移)、點云重疊度、是否存在其他傳感器提供初始值以及初始值的質量；

(3)與環境有關的因素，包括場景類型如室內/室外、結構化/非結構化場景，環境中的動態目標以及遮擋程度。

關于掃描匹配方法評價的早期研究主要關注收斂速度和最終結果的精度[34]。對于精度的評價，平移分量較為簡單，直接利用歐式距離即可；而對于旋轉分量精度的評價有多種不同方法，文獻[100]將3D掃描數據與2D的位姿真值融合，評價在2D空間中進行，通過方位偏差絕對值來評價旋轉分量精度，統計量采用標準差和最大誤差。文獻[101]對6種用于SO(3)的距離進行了評價，結果表明歐拉角差的范數不是一種距離，而采用單位球上的測地距離更可取。

文獻[27]對比了ICP、GICP和NICP算法。文獻[102]研究了匹配算法對于初始不對準的魯棒性，在收斂域、魯棒性和配準精度3個方面對比了ICP和3D-NDT方法。結果顯示：3D-NDT方法處理更快，能夠從偏離真值較大的初值達到收斂，但可能在初值偏差較小的情況下匹配失敗，因而相對來說ICP表現更可預見。文獻[103]研究了低重疊度對配準算法的敏感度，并用于預測掃描匹配的失敗。文獻[104]評價了一個局部方法NDT和一個全局掃描配準方法MUMC(Minimally Uncertain Maximum Consensus)。利用仿真進行掃描匹配方法對比也是一種行之有效的方法，如文獻[34]利用仿真數據，針對不同的空間約束和傳感器噪聲對比了ICP的變種算法。文獻[105]針對室內環境，仿真分析了何種LiDAR采用何種掃描匹配方法最優，對比了標準ICP、CSM、MbICP、PSM和2D-NDT 共5種算法，并給出了選擇建議。

科學方法的一個關鍵部分是性能測試實驗能夠被其他研究人員重復實現以便比較不同的結果。通常，文獻中進行掃描匹配算法驗證時往往選擇較為簡單的適合相應算法的場景與某一到兩種其他方法進行對比，未測試或只測試上述個別因素對掃描匹配的影響；并且，同一算法在不同文獻中有不同的實現，這使得多種算法的嚴格對比難以實現。文獻[35]在激光掃描匹配方法評價方面具有里程碑意義，提出了利用公開數據集系統評價ICP及其改進算法的首套規范，已成為許多學者評價激光掃描匹配方法的事實標準[90]。此外，該文還開源了一個模塊化的ICP庫，使得在同一框架下對比不同ICP改進算法成為可能。

目前，對激光掃描匹配的大規模深入研究仍然較少。文獻[90]首次將文獻[35]提出的規范用于評價非ICP方法，同時指出文獻[35]提出的基準存在重大缺陷：首先，來自數據集的可用掃描數據對的選擇較少，因而限制其應用于全局掃描匹配方法；其次，所提供的初始偏移往往是不切實際的，而掃描重疊度通常較低，雖然這使得數據集更具挑戰性，但限制了其在更符合實際情況下的辨別力。相應地，文獻[90]提出了對于掃描匹配評價測試規范[35]的修改建議：

(1)采用固定大小的位姿偏移(如文獻[86])，而不是從正態分布中采樣得到(即加方差一定的高斯噪聲)；

(2)提供更多確定可用的掃描對，大量的初始位姿估計只對局部方法有意義，對于不需要初值的全局方法，提供更多的掃描數據對及其真值更為重要。

6 總結與展望

回顧激光掃描匹配方法的發展變化，從最初的基于點的掃描匹配，到基于特征的掃描匹配，再到基于正態分布變換等數學性質的掃描匹配，對掃描數據(即場景的采樣)的表示形式越來越高級；新的方法松弛甚至完全脫離了傳統方法的假設，使得模型越來越逼近真實情況，從而得到越來越精確、魯棒的結果；采用由粗到精的“兩步法”逐漸成為掃描匹配的標準方案，混合掃描匹配方法能夠揚長避短，從而提升系統的可靠性；隨著硬件計算能力的提升，一些求解更準確但計算復雜度較高的方法變得可實時運行，加速了場理論、譜技術、智能優化算法等移植到掃描匹配的進程。總的來說，激光掃描匹配已經得到了相當程度的發展，其中ICP類方法、基于特征的方法以及NDT類方法是目前發展較為成熟、應用相對廣泛的代表性解決方案，但仍然存在一些亟待完善和解決的問題，同時也是激光掃描匹配研究的發展方向，可能包括但不限于：

(1)降低掃描匹配旋轉分量誤差，旋轉參數誤差往往與平移參數誤差在同一量級，但在較遠處造成的實際偏差往往很大，使測得的圖不準，誤差累積后漂移嚴重；

(2)應對掃描點云運動畸變問題，由于傳感器隨載體快速運動，掃描點云產生變形難以匹配，尤其是采用低速旋轉3D LiDAR時[22]；

(3)有效處理動態場景中的動態目標，首先是識別和跟蹤，然后是如何處理(如采用降權的方式，而不一定是直接剔除的方式)；

(4)長期運行而又不閉環情況下如何減小掃描匹配的累積誤差，即漂移問題；

(5)尋求新的魯棒高效的3D特征點，包括檢測算法和特征描述子；

(6)混合掃描匹配算法，魯棒于不同的環境條件，如重疊度變化、環境結構性條件變化以及高動態(如大旋轉角)，可自適應調整參數[67]、切換或有效組合不同方法；

(7)故障監測，即有效預測和檢測掃描匹配失敗；

(8)運用深度學習等人工智能技術來解決掃描匹配問題[106]；

(9)結合語義信息進行掃描匹配(如利用語義信息輔助ICP算法中的對應點匹配[107])。