基于小波神經網絡的光纖陀螺誤差補償方法

騫微著，楊立保

(1.中國科學院 長春光學精密機械與物理研究所，吉林 長春 130033； 2.中國科學院大學，北京100039； 3.長春理工大學 機電工程學院，吉林 長春 130022)

1 引 言

光纖陀螺利用光纖的Sagnac 效應來測量慣性空間的角速率，具有測量精度高、穩定性好、動態范圍大等優點，目前已被廣泛用于穩定平臺和導航系統中。在光纖陀螺受到外界條件影響后會產生漂移誤差，影響其測量精度。因此對于光纖陀螺誤差補償的研究近年來已經成為熱點。目前普遍采用的誤差補償方法有ARMA[1]模型和Kalman算法[2-3]。其中，ARMA是一種線型模型，其假設誤差為零均值、平穩的正態時間序列。而Kalman算法要求獲得準確的噪聲先驗統計信息[4]。這些都影響了這些方法對誤差的建模精度和補償效果。不同于ARMA模型和Kalman算法，神經網絡是一種基于非參數辨識的建模方法。神經網絡在獲得足夠多的信號樣本后，便可以獲得光纖陀螺的誤差在頻域上的特性。使用足夠多的樣本信號對誤差進行建模之后，可獲得到光纖陀螺信號的頻率特征。因此，神經網絡模型具備良好的信號建模能力。常用的神經網絡有BP(Back Propagation )神經網絡和徑向基(Radial Basis Function,RBF)神經網絡[5-6]。BP神經網絡作為一種全局逼近神經網絡，一般采用Sigmoid函數作為激勵函數。而Sigmoid函數是全局激勵函數，在神經網絡的訓練過程中很容易陷入局部極小值[7]。RBF網絡雖然是一種局部逼近網絡，但是由于采用高斯基函數作為逼近函數，不能像小波函數那樣具有尺度縮放的能力，因此難以實現高精度的逼近效果[8]。Q.Zhang和A.Benvensite提出一種激勵函數為小波函數的小波神經網絡(Wavelet Neural Network,WNN)[9]。由于小波函數是一種正交的局部逼近函數，且具有在空間平移和縮放的能力，因此其逼近效果要優于BP神經網絡和RBF神經網絡。

本文首先使用小波分析中的Mallat算法提取光纖陀螺信號中趨勢項后的誤差余項[10]，將其作為神經網絡的目標輸出，而將光纖陀螺的原始角速率信號作為學習樣本，將與之對應的誤差作為神經網絡的輸出。針對梯度下降法的不足，使用改進后的訓練方法訓練神經網絡。在建立小波神經網絡模型后，對其建模準確性進行了檢驗。為了驗證本文方法對光纖陀螺誤差補償的有效性，將最終的補償效果與其他方法進行了對比。

2 提取光纖陀螺的誤差

對光纖陀螺的誤差建模時，需要對其輸出信號中的趨勢項和誤差項進行分離。傳統的逐步回歸法把光纖陀螺的趨勢項分為線型項和周期項，線性項用去均值法除去而周期項用周期圖法擬合。這種方法不僅十分繁瑣，而且將趨勢項簡單分為線型項和周期項，不能準確識別信號的特征[11]。而采用小波分析中基于多尺度分析的Mallat算法，可以將光纖陀螺的信號在不同尺度下進行分解，從而能有效地分離出信號中有用的低頻分量和高頻噪聲分量。

Mallat分解算法中的小波函數，選擇具有緊支撐和正交特性的Daubechies小波，階數為6階，其相應的尺度函數和母小波函數分別為φj,k(t)和ψj,k(t)。若待分析信號是一個平方可積函數，f(t)∈L2(R)，R為實數域。在分辨率為2-j下，信號小波分解的逼近項Cjf(t)和細節項Djf(t)分別可以表示為：

(1)

式中，cj,k為分辨率2-j下的逼近項系數，cj,k=〈f(t),φj,k(t)〉。dj,k為分辨率2-j下的細節項系數，dj,k=〈f(t),ψj,k(t)〉。其中，〈·〉表示內積運算。將分辨率為2-j-1下的逼近項和細節項分別表示為Cj+1f(t)和Dj+1f(t)。則Cjf(t)的唯一分解可表示為：

Cjf(t)=Cj+1f(t)+Dj+1f(t) . (2)

因此，根據式(2)就可以對信號在不同尺度下不斷地進行分解。信號在M尺度下分解即可表示為：

C0f(t)=CMf(t)+D1f(t)+D2f(t)…DMf(t) . (3)

根據式(3)，在光纖陀螺信號小波重構時，可以分離出逼近項CMf(t)，對D1f(t),D2f(t)…DMf(t)等細節項進行單獨重構。這樣便可得到提取出趨勢項后光纖陀螺信號的誤差余項。根據基于多尺度分析原理，隨著分解尺度M不斷增大，獲得的像越粗糙，其表征的漂移主趨勢就越明顯。因此為了盡可能地分離出趨勢項，可不斷增大M值[12-13]。為了驗證在M尺度分解下確實已提取出了趨勢項，可以對原始信號和重構信號的功率譜密度進行分析[14]。若在重構信號的功率譜密度中低頻項已經完全去除，則可以認為趨勢項已被提取出來，否則繼續增加M值。

3 小波神經網絡建模

3.1 小波神經網絡

小波變換的基本思想是利用一簇小波函數來逼近某一函數或者信號。而這一簇小波基函數ψm,n均由某一個母小波基函數ψ經過平移和尺寸伸縮得到的。小波基函數與母小波函數的關系為：

ψm,n=2m/2ψ(2mt-n) , (4)

其中，m,n∈Z。

由于小波函數的特有性質，因此在小波神經網絡中，隱藏層節點的激勵函數只在局部范圍內影響網絡的輸出。這在網絡訓練過程中可以有效避免節點間相互影響，并且使網絡具有良好的泛化能力。

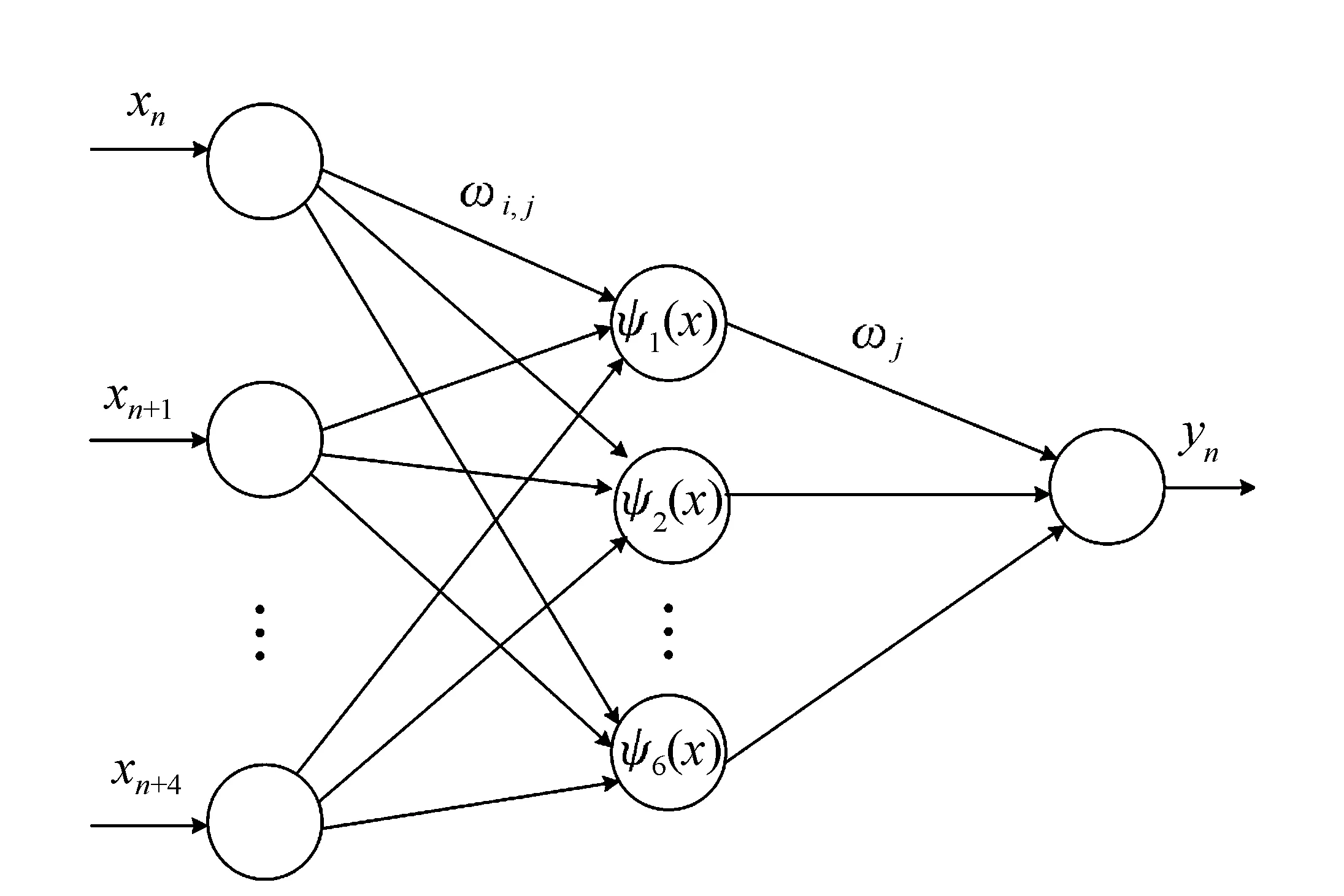
圖1 小波神經網絡拓撲結構 Fig.1 WNN topological structure

圖1中所示的小波神經網絡拓撲結構與BP神經網絡類似，也是一種前向網絡，其信號向前傳播而誤差向后傳播。神經網絡的輸入為xn,xn+1…xn+4，因此隱含層輸出可以表示為：

(5)

式中，輸入點個數k=5，h(j)為隱含層第j個節點的輸出值，wi, j為輸入層和隱含層的連接權值，aj為小波函數的尺度因子，bj為小波函數的平移因子。ψj為小波基函數。本文選擇的小波基函數為Morlet小波函數，其表達式為ψ(x)=e-x2/2·ejω0x，為了使其具有近似支撐性和滿足容許條件[10]，取w0=6。設小波神經網絡的輸出為yn，則小波神經網絡的輸出表達式為：

(6)

式中，wj為小波神經網絡隱含層到輸出層的權值。

3.2 對小波神經網絡訓練過程的改進

小波神經網絡輸出誤差e(n)的定義為：

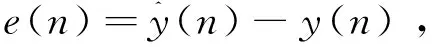
(7)

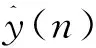
(8)

為了使目標函數達到最小值，可以使用共軛梯度法，BFGS法，最陡下降法等[7]。本文使用最陡下降法來更新權值wi, j、wj和參數aj、bj。根據小波神經網絡的預測誤差得到各個神經網絡權重的調整值：

(9)

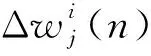
(10)

式中,η2為小波函數中參數的學習速率。然后根據式(9)和式(10)得到更新的神經網絡權值和小波函數參數：

(11)

由于小波神經網絡的網絡權值和函數參數的訓練方法采用了固定學習速率的梯度下降法。該方法在學習過程中容易陷入極小值且收斂緩慢[15]。針對這個問題，可以采用增加動量因子避免陷入極小值，同時采用自適應調整學習速率的方法來加快學習速度。

增加動量因子方法是在神經網絡權值和參數更新時，在計算公式中分別增加一個動量項。這樣便可以減小神經網絡對局部極小值的敏感性，防止神經網絡在訓練過程中陷入局部極小值后無法逃脫。增加動量因子后的神經網絡權值和參數更新公式為：

(12)

式中，η3為動量因子學習速率。

自適應調整學習速率算法的基本思想是讓學習速率隨著訓練次數在線調整。首先使學習速率從一個較小的值開始，如果在訓練過程中誤差減小，則增加學習速率，若在訓練過程中誤差增大則減小學習速率。學習速率自適應調整公式如下：

(13)

4 實驗結果與分析

4.1 誤差的神經網絡建模

在采集光纖陀螺的原始信號時，將光纖陀螺放置在一個恒速率轉臺上，該轉臺的理想輸出角速率為-60(°)/s。光纖陀螺的原始采集信號及在12尺度下提取的趨勢項如圖2所示。

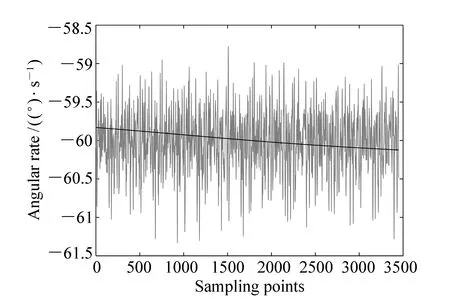
圖2 原始采集信號及主趨勢項 Fig.2 Original acquisition signal and main trend term

從圖2可以看出，在12尺度下提取的趨勢項在最大程度上分離出了光纖陀螺信號的低頻分量，從而表征出了陀螺信號的漂移主趨勢。

為了驗證在該尺度分解下確實已提取出了趨勢項，可以對原始信號和重構信號的功率譜密度進行分析，結果如圖3所示。

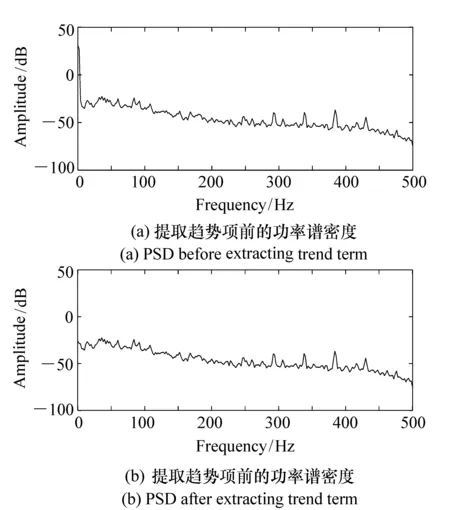
圖3 提取趨勢項前后的功率譜密度 Fig.3 PSDs before and after extracting trend term

在圖3中，圖(a)為分離趨勢項前的功率譜密度圖，圖(b)為分離趨勢項后的功率譜密度圖。從兩圖對比可以看出，原始信號的低頻分量在經過小波分解重構后已被提取出。因此，根據圖2和圖3可知，在12尺度下分解重構后的殘差信號即為去掉趨勢項的噪聲信號。

使用2 500個光纖陀螺信號已分離出趨勢項的誤差余項作為神經網絡的目標輸出，并把2 500個光纖陀螺原始輸出的角速率信號作為學習樣本。使用改進后的訓練方法訓練小波神經網絡200次，得到光纖陀螺誤差的神經網絡模型。訓練過程中累積絕對誤差變化見圖4。

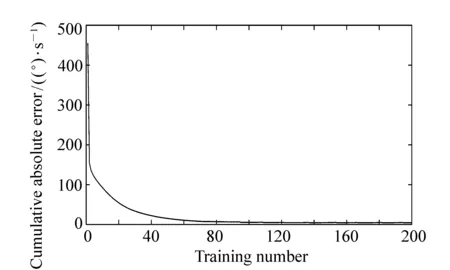
圖4 小波神經網絡訓練過程 Fig.4 WNN training process

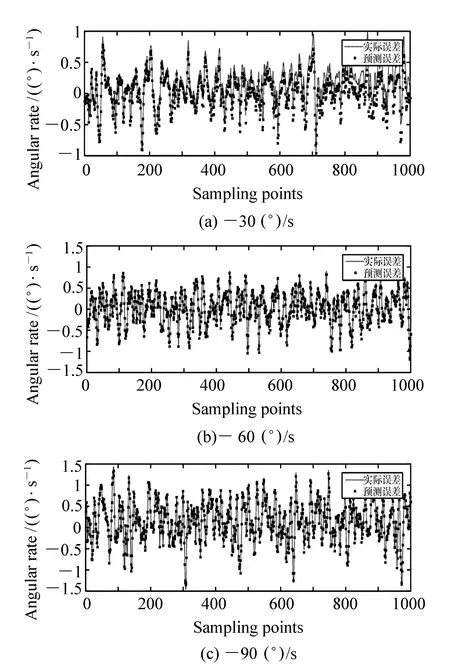
圖5 神經網絡預測的不同測試信號誤差預測值 Fig.5 WNN predication trends of three different test signal errors

圖4所示的結果表明，使用經過改進的訓練方法訓練后，小波神經網絡在對光纖陀螺誤差建模過程中可以迅速收斂。大約在訓練100次后即達到最優。

在神經網絡訓練結束之后，可得到光纖陀螺誤差的模型。為了檢驗該神經網絡模型是否準確，選取1 000個不同于樣本信號的測試信號對之前建立的神經網絡模型進行驗證。為了驗證該模型的泛化性能，在其它速率范圍(-30 (°)/s和-90 (°)/s)也分別選取了1 000個測試信號進行測試，結果見圖5。

從圖5的結果可以看出，建立的小波神經網絡模型對不同速率下測試信號的誤差均可進行準確估計。這表明該小波神經網絡模型已經獲得了光纖陀螺誤差在頻域上的特性。

4.2 誤差補償的效果評價

從原始信號中去除神經網絡預測誤差，便可以對光纖陀螺的原始信號進行補償。為了驗證本文提出算法的有效性，將光纖陀螺信號補償前后的功率譜密度進行分析，結果如圖6所示。

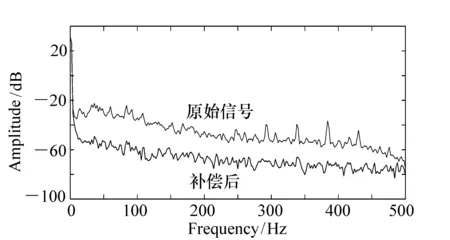
圖6 誤差補償前后的功率譜密度 Fig.6 PSDs before and after error compensation

圖6的結果表明，經過本文方法對光纖陀螺原始信號進行誤差補償后，信號的有用低頻信息被保留而高頻的噪聲分量被削弱。

將本文補償方法對光纖陀螺的原始信號的補償效果和軟閾值小波濾波算法、Kalman濾波算法的補償效果進行對比。其結果如圖7所示。

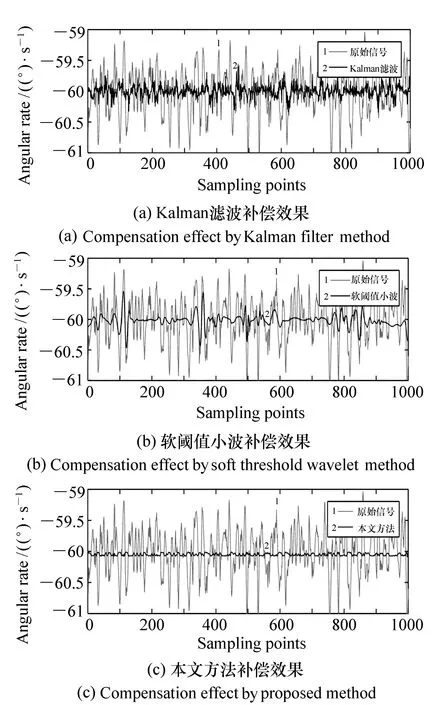
圖7 不同方法對陀螺的補償精度 Fig.7 Compensation effects for gyro by different methods

從圖7所示的結果可以看出，相較于Kalman算法和軟閾值小波算法，小波神經網絡補償方法可以更為準確地對光纖陀螺誤差進行補償，并且補償后的光纖陀螺信號更為平穩，更接近光纖陀螺的真實輸入。各種方法補償后的精度(信號輸出的標準差)和運算耗時見表1。

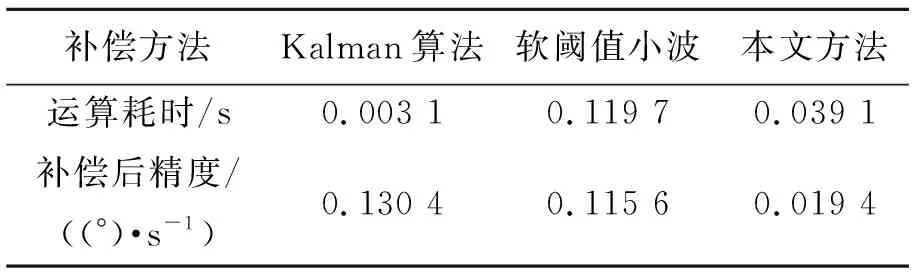
表1 不同算法的補償效果

從表1的數據可以看出，在算法的運算時間上，本文算法耗時大于Kalman算法但要小于軟閾值小波算法。而在對誤差的補償精度上，經過小波神經網絡補償后的光纖陀螺原始信號的輸出精度要優于傳統的Kalman算法和軟閾值小波濾波算法。

5 結 論

針對光纖陀螺誤差難以準確補償的問題，提出了一種基于小波神經網絡的補償方法。首先使用了小波分析中的Mallat分解算法，在12尺度下分離出了陀螺噪聲的誤差項和趨勢項，并對誤差項進行了單獨重構。然后對重構信號使用小波神經網絡進行建模和補償。同時為了提高小波神經網絡的學習速率和準確性，采用了增加動量因子和自適應調整學習速率的方法，改進了小波神經網絡的性能。通過比較本文算法和Kalman算法及軟閾值小波算法的誤差補償效果發現，光纖陀螺輸出的精度提高到了0.019 4°/s。采用本文方法對光纖陀螺誤差所建立的神經網絡模型，不僅可以對誤差進行準確建模并且補償效果也要優于其他方法。本文方法對研究光纖陀螺誤差補償有一定的工程實用和理論參考價值。