二維有機拓撲絕緣體的研究進展?

高藝璇1)3) 張禮智1) 張余洋1)2)3) 杜世萱1)2)3)?

1)(中國科學院物理研究所,納米物理與器件實驗室,北京 100190)

2)(中國科學院物理研究所,松山湖材料實驗室,東莞 523808)

3)(中國科學院大學,中國科學院拓撲量子計算卓越創新中心,真空物理重點實驗室,北京100049)

(2018年9月14日收到;2018年10月16日收到修改稿)

1 引 言

二維拓撲絕緣體也被稱為量子自旋霍爾絕緣體[1],與整數量子霍爾效應息息相關[2,3].二維拓撲絕緣體在帶隙中存在具有自旋選擇功能的邊界態[4?7],這些邊界態受拓撲保護而不受彈性背散射和局域化的限制,在自旋電子學和量子計算機等領域有著廣闊的應用前景.迄今為止,人們已經在HgTe/CdTe和InAs/GaSb/AlSb兩類超晶格材料體系中實現了量子自旋霍爾效應[8,9].隨后,科學家預測Bi雙層[10?14]和錒基雙層化合物[15]是新的二維和三維拓撲絕緣體.最近,基于半導體表面的Bi單層二維拓撲絕緣體的理論預言[16,17]也被實驗證實[18].然而這些拓撲絕緣體都是無機材料.與無機材料相比,有機材料具有成本低,易于制造和機械彈性性能好等諸多優點,同時有機材料和基于有機材料的器件也可以實現許多傳統的無機材料和基于無機材料的器件具有的物性,例如有機超導[19]、有機發光二極管[20]和有機場效應晶體管[21]等.有趣的是,最近有理論工作預測金屬有機晶格中也存在二維拓撲絕緣體[22?25].與二維無機拓撲絕緣體的性質類似,二維有機拓撲絕緣體同樣存在自旋軌道耦合導致的帶隙和連接價帶和導帶的拓撲邊界態.由于二維無機拓撲絕緣體的種類受到晶體對稱性和原子軌道的限制,數量有限.對于二維金屬有機材料,由于有機分子的種類豐富,有機分子與金屬原子的配位多樣,使得可能存在更多二維有機拓撲絕緣體.二維有機拓撲絕緣體的研究進一步擴展了有機材料在自旋電子學中的應用,激發了科學家們的興趣.隨著合成化學和納米技術的不斷發展,科學家們預言并制備了越來越多的二維有機拓撲絕緣體[22?34].

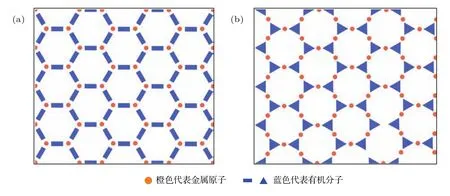
圖1 兩類二維有機拓撲絕緣體結構示意 (a)六角對稱的金屬有機晶格;(b)Kagome金屬有機晶格Fig.1 . of the two types of organic topological insulators:(a)Hexagonal metal-organic lattice;(b)Kagome metal-organic lattice.

迄今為止,二維有機拓撲絕緣體可以歸結為兩類.第一類具有六角對稱結構,在這類材料中,金屬原子組成六角對稱結構并與相鄰三個分子成鍵[22?24],如圖1(a)所示.第二類具有Kagome結構[25?27,35?38],在這類材料中,金屬原子組成Kagome結構,并與相鄰的兩個分子成鍵[25?27],如圖1(b)所示.本文按照有機拓撲絕緣體的發展歷程,對這兩類有機拓撲絕緣體的代表工作及最新研究進展進行了介紹.

2 六角對稱的金屬有機晶格

2013年,Liu團隊[22?25]首次從理論上預言了由金屬有機晶格構成的六角對稱的二維有機拓撲絕緣體.他們以三苯基金屬化合物作為基本單元,每個金屬原子對稱地與三個苯環相連,在三重旋轉對稱性下傾向于自組裝成六角晶格.利用具有強自旋軌道耦合的重金屬原子Pb組成Pb(C6H5)3晶格,如圖2(a)所示.由于Pb原子具有6s26p2的電子結構且傾向于sp3雜化,平面內的Pb原子分別向苯環平面的上下方向移動造成結構的翹曲,如圖2(a)的側視圖所示.計算得到的晶格常數為12.36 ? (1 ? =0.1 nm),Pb—Pb的距離(l)和高度差(h)分別為7.46 ?和2.18 ?.不考慮自旋軌道耦合時,金屬有機晶格的能帶結構在K點存在一個狄拉克點,費米能級恰好位于狄拉克點處,如圖2(b)和圖2(c)所示,圖2(b)中虛線代表費米能級,插圖是材料的第一布里淵區.考慮自旋軌道耦合后,在K點處會打開8.6 meV的能隙,如圖2(f)和圖2(g)所示.利用第一性原理計算的結果可以擬合得到以最大局域化的萬尼爾(Wannier)函數為基礎的緊束縛哈密頓量[39].利用這些最大局域萬尼爾函數,可以構建半無限拓撲絕緣體晶格的格林函數[40],并計算出邊界的局域態密度.圖2(d)為由萬尼爾函數和第一性原理計算所得的能帶結果,兩者符合得非常好.從圖2(e)中給出的邊界局域態密度可以看出(L為原胞沿著邊界的長度),非平庸的拓撲邊界態連接價帶和導帶,證明了這種有機材料是二維拓撲絕緣體.

Pb(C6H5)3晶格的拓撲性質可以由K(K′)點附近的物理性質來決定,因此可以用有效哈密頓量來刻畫它的低能性質: Hη=}νF(kxτx? ηkyτy)+ ητzh11+ ε0I, 其 中h11=?λSOσz? aλR(kyσx?kxσy),η= ±1分別對應K點和K′點,σ(τ)為自旋(子晶格)的泡利矩陣,νF為費米速度,ε0為格點能量,I為4×4的單位矩陣,λSO為有效自旋軌道耦合,λR為Rashba自旋軌道耦合強度,a為晶格常數.通過擬合第一性原理的結果,得到的擬合參量分別是ε0=0 eV,}νF=1.13 eV·?, λSO=0.0043 eV,aλR=0.316 eV·?.在模型中有一項非零的Rashba自旋軌道耦合,這一非零項在平面的石墨烯結構中并不存在,在這里是由于結構的翹曲造成的.結構的翹曲使原胞中的兩個金屬原子在不同的平面上,導致既有平面內又有平面外的自旋軌道耦合[41].平面內的自旋軌道耦合與石墨烯一樣,導致了能隙的打開;而平面外的自旋軌道耦合(石墨烯中不存在),使得z方向存在勢能梯度[41],對狄拉克點處的能量色散關系有微小的改變,但對拓撲性質沒有影響.用Bi原子替代Pb,可以得到與Pb(C6H5)3相似的拓撲性質,并且存在更大的帶隙(43 meV).此外,這類拓撲有機晶格對應力很不敏感,施加±10%的應力時,仍然保持著非平庸的拓撲性質.如果利用過渡金屬元素(例如Mn)替換Pb,還可以進一步得到量子反常霍爾絕緣體[23].

金屬有機化學和基底調制的分子自組裝是合成二維共價有機結構的成熟方法.最近,研究者成功合成出了由金屬—碳和碳—碳等有機化學鍵組成的定向二維共價有機物[42?48].這一突破為合成此類有機拓撲結構提供了可能,在未來的實驗中極有可能合成出高質量、大尺寸的此類薄膜材料.

圖2 六角對稱的二維金屬有機晶格Pb(C6H5)3的原子結構和電子性質[22] (a)二維Pb(C6H5)3原子結構頂視圖與側視圖,虛線表示單位原胞,l和h表示原胞中兩個金屬原子的距離和高度差;(b)不考慮自旋軌道耦合時的Pb(C6H5)3晶格的能帶結構,虛線代表費米能級,插圖是材料的第一布里淵區;(c)不考慮自旋軌道耦合時狄拉克點附近能帶結構的放大圖,紅點是用有效哈密頓量擬合的能帶,實線是第一性原理計算的能帶;(d)第一性原理和萬尼爾能帶結構在狄拉克錐附近的比較;(e)半無限晶格的鋸齒形邊界處的局域態密度,L是原胞沿著邊界的長度;(f)考慮自旋軌道耦合之后的Pb(C6H5)3晶格的能帶結構;(g)狄拉克點附近能帶結構的放大圖[22]Fig.2 .Atomic structure and electronic properties of monolayer Pb(C6H5)3in a hexagonal metal-organic lattice[22]:(a)Top and side views of the 2D metal-organic superlattice;(b),(f)band structures of metal-organic lattice without and with spin-orbit coupling(SOC),respectively,the dashed line indicates the Fermi level.The inset shows the f i rst Brillouin zone,and Γ,K,M and K′are the high symmetric k-points;(c),(g)zoom-in band structures around the Dirac point without and with SOC,respectively,the red dots are the f i tted bands using the ef f ective Hamiltonian,and black lines are the f i rst-principles band structures;(d)band structures calculated by f i rst-principles and Wannier functions around the Dirac-cone;(e)energy and momentum-dependent local density of state of the zigzag edge of the semi-inf i nite lattice,L is the unit cell length along the edge.

3 Kagome金屬有機晶格

除了前文提到的具有六角對稱的二維有機拓撲絕緣體,人們也在嘗試設計并在實驗中尋找具有新型結構的有機拓撲材料.經過不斷的嘗試,Wang等[25]發現了具有Kagome晶格的第二類二維有機拓撲絕緣體.在這類材料中金屬原子組成Kagome晶格,并與相鄰的兩個分子成鍵[25?27,35?38].而由Kambe團隊[35]在實驗上合成出來的Ni3C12S12金屬有機晶格(圖3(a))就具有Kagome結構,屬于第二類二維有機拓撲絕緣體.

圖3(a)展示了二維Ni3C12S12的晶格結構,虛線和實線分別代表Kagome晶格和單位原胞,計算得到的晶格常數是14.63 ?,與實驗上的14—15 ?[35]符合得很好.通過第一性原理計算可進一步得到Ni3C12S12的能帶結構.考慮自旋軌道耦合效應之后,可以清晰分辨出在費米能級附近存在三條典型的Kagome能帶:一條平帶,兩條狄拉克帶,如圖3(c)紅色線條所示(所有的能帶都是自旋退簡并的).圖3(d)是圖3(c)中Kagome能帶的放大圖,狄拉克點附近的帶隙?1=13.6 meV,平帶和狄拉克頂的帶隙?2=5.8 meV.存在拓撲邊界態是二維拓撲絕緣體的重要判據,從邊界局域態密度(圖3(b))可以清楚地看到與體帶邊緣連接的非平庸的拓撲邊界態.

在Kagome晶格上使用單軌道緊束縛模型[49]來描述晶格的電子態特性,相應的哈密頓量在倒空間可以寫成如下形式:

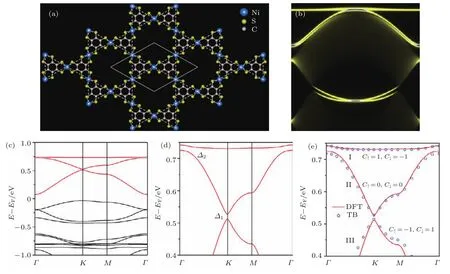
圖3 二維Kagome金屬有機晶格Ni3C12S12的結構和電子性質[25] (a)結構頂視圖,虛線和實線分別代表Kagome晶格和單位原胞;(b)自旋軌道耦合帶隙內的半無限狄拉克邊界態(包含自旋向上和自旋向下);(c)沿高對稱方向的能帶結構(考慮了自旋軌道耦合);(d)Kagome能帶在兩個自旋軌道耦合帶隙附近的放大圖;(e)第一性原理和單軌道緊束縛計算獲得的兩個自旋軌道耦合帶隙(?1和?2)附近的能帶結構對比Fig.3 .Atomic structure and electronic properties of monolayer Ni3C12S12in a Kagome metal-organic lattice[25]:(a)A top view of the atomic structure,the solid and dashed lines show the unit cell and the Kagome lattice,respectively;(b)semi-inf i nite edge states(both spin up and spin down components)within the SOC gaps;(c)band structure along the high symmetric directions;(d)zoom-in Kagome bands around two SOC gaps;(e)comparison between f i rst-principles and single-orbital tight-binding(TB)band structures for the f l at and Dirac bands(?1and ?2).

為了確認Ni3C12S12晶格的能帶拓撲性質,利用Kube公式[50,51]分別計算了具有不同自旋的能帶陳數(C=C↑+C↓)和自旋陳數[Cs=對于在費米能級附近的三條Kagome能帶,平帶和底部狄拉克帶具有非零的陳數(±1),而頂部狄拉克帶的陳數為零,標在圖3(e)中.因此,在自旋軌道耦合帶隙(?1和?2)內,陳數為0,而自旋陳數為?1,這表明Ni3C12S12薄膜具有非平庸的拓撲性質.

由于過渡金屬原子非常容易與分子的硫原子(或者是氧原子)形成配位鍵,這一類含硫元素的二維金屬有機共價材料很容易合成[35?38].此外,通過替換不同的分子與金屬原子,不僅可以調節材料的帶隙[26,30],還可以得到磁性有機拓撲絕緣體,實現量子反常霍爾效應[34].

4 本征二維有機拓撲絕緣體——Cu-DCA(dicyanoanthracene)分子薄膜

迄今為止,實驗合成的第二類有機拓撲絕緣體都不具有本征拓撲性[25?27,35?38,52],在進行拓撲特性測量之前,需要通過電子或者空穴摻雜,將費米能級調控到自旋軌道耦合帶隙中[25?27].作為配位聚合物材料,金屬有機晶格通常是根據配位化學的特定電子計數規則形成的.不改變幾何結構的非等價摻雜很困難,例如用不同價態的外來金屬原子代替主體金屬原子等,會改變材料的配位化學性質.對于重摻雜情況,可能所有的主體金屬原子都要被替換,直到化學計量極限[53].金屬有機晶格的摻雜可以通過氧化還原改變金屬離子氧化態的方式來實現[54],然而這種方法仍受限于實際可達到的摻雜量.因此,人們仍致力于尋找本征二維有機拓撲絕緣體并實現拓撲態的直接測量.基于對兩類有機拓撲晶格的研究,Zhang等[55]發現第一類六角對稱晶格最有可能形成本征的有機拓撲絕緣體.通過對大量的實驗結構進行金屬原子和分子軌道之間的雜化分析,文獻[56—58]在現有實驗合成的材料Cu-DCA二維有機薄膜中發現了一類本征的二維拓撲絕緣體[55].

9,10-DCA分子含有三個苯環和兩個氰基(圖4(a)).由于氰基中孤對電子的存在,該分子很容易與一些過渡金屬原子形成強配位鍵.例如,在Cu(111)表面的雙層NaCl上可以合成出線性Fe(DCA)2和Ni(DCA)2絡合物[59].最近,有兩個研究組報道了在Cu(111)表面上生長的Cu-DCA二維薄膜[56,57],如圖4(b)所示,白色箭頭指向區域邊界,插圖是高分辨掃描隧道顯微鏡(STM)圖像[57].為了削弱分子薄膜與金屬襯底之間的相互作用,有研究組已經在外延石墨烯襯底上合成出了Co-DCA金屬有機結構[58],如圖4(c)所示.圖4(a)給出了Cu-DCA薄膜原子結構,其中Cu原子構成了六角(蜂窩狀)晶格(紅色虛線),而DCA分子構成了Kagome晶格(藍色虛線)[49].每個Cu原子與來自DCA分子的三個氰基成鍵,形成非常強的配位鍵(Cu—N鍵長度約為1.88 ?).在每個晶胞中,有兩個Cu原子和三個DCA分子.計算得到的Cu-DCA薄膜的晶格常數為20.36 ?,與實驗結果(20.8 ?±0.2 ?)非常一致[57].僅考慮這類材料的幾何結構,它們屬于第一類二維有機拓撲絕緣體,即金屬原子以六角晶格排列.

圖4(d)顯示了Cu-DCA薄膜的能帶結構和投影態密度,可以看到費米能級附近的典型的Kagome能帶特征[36,49,60],Kagome能帶由兩個狄拉克能帶和一個帶寬為3.0 meV的平帶組成.根據投影態密度,所有的Kagome能帶主要來自DCA分子的pz軌道,從Kagome能帶對應的局域電荷密度分布圖(圖4(d)右上角插圖)中也能得出相同的結論.最重要的是,與之前人們所研究的Kagome系統不同[25?27,35?38],這一系統費米能級恰好位于狄拉克點處.圖4(d)底部兩個插圖分別表示忽略和考慮自旋軌道耦合的能帶.在考慮自旋軌道耦合之后,狄拉克點附近有帶隙(?1=2.9 meV)打開,使得費米能級正好位于自旋軌道耦合帶隙內,表明與自旋軌道耦合相關聯的固有的拓撲態是本征的.

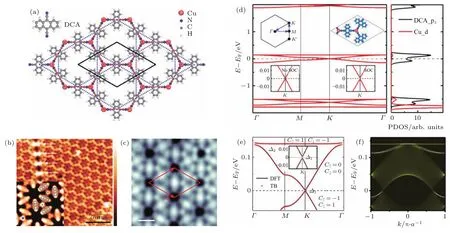
圖4 二維Cu-DCA金屬有機晶格的原子結構和電子性質 (a)二維Cu-DCA結構的頂視圖,左上角插圖是DCA分子結構示意圖,紅色虛線、藍色虛線和黑線分別代表Cu原子的蜂窩狀晶格,DCA分子的Kagome晶格和單位原胞[55];(b)室溫沉積在Cu(111)表面上的Cu-DCA自組裝結構的STM圖像,白色箭頭指向區域邊界,插圖是高分辨STM圖[57];(c)在Gr/Ir(111)表面上Co2(DCA)3金屬有機結構的STM圖像,左下角的比例尺是1 nm[58];(d)Cu-DCA薄膜的能帶結構和投影態密度,其中右上角插圖表示費米能級附近的電荷密度分布,底部兩個插圖分別表示忽略和考慮自旋軌道耦合的能帶[55];(e)第一性原理和緊束縛計算的兩個自旋軌道耦合帶隙(?1和?2)附近的能帶結構[55];(f)自旋軌道耦合帶隙內的半無限狄拉克邊界態[55]Fig.4 .Atomic structure and electronic properties of 2D Cu-DCA:(a)Top view of the atomic structure,the inset shows the conf i guration of DCA molecule,the red dashed,blue dashed,and black lines outline the honeycomb lattice of the Cu atoms,the Kagome lattice of the DCA molecules,and the unit cell,respectively[55];(b)STM image of self-assembled structure of DCA on Cu(111)after deposition at room temperature,the white arrows mark a domain boundary,inset is high resolution STM image measured with a DCA modif i ed tip[57];(c)STM topography image of Co2(DCA)3on Gr/Ir(111)surface[58];(d)band structures and PDOS,where the top right inset indicates the charge distribution around the Fermi level,and the bottom two insets show the zoom-in bands without and with SOC,respectively[55];(e)band structures around two SOC gaps(?1and?2)calculated by the f i rst-principles and single-orbital TB calculations[55];(f)semi-inf i nite Dirac edge states within the SOC gaps[55].

圖4(e)分別利用第一性原理(黑線)和單軌道緊束縛(紅點)計算了體系的能帶結構,兩者之間具有很好的一致性.由于費米能級附近的Kagome能帶主要來自DCA分子的pz軌道,因此該分子可以被近似地看作一個超原子.Kagome晶格中的DCA分子之間的電子躍遷由Cu原子連接,從而使得自旋軌道耦合增強,自旋軌道耦合帶隙(?1和?2)大于純碳元素材料中的自旋軌道耦合帶隙.為了確認Cu-DCA能帶的拓撲性質,利用Kube公式分別計算了具有不同自旋的能帶陳數(C=C↑+C↓)和自旋陳數對于在費米能級附近的三條Kagome能帶,平帶和底部狄拉克帶具有非零陳數(±1),而頂部狄拉克帶的陳數為零,標在圖4(e)中.因此,在自旋軌道耦合帶隙(?1和?2)內,陳數為0,而自旋陳數為?1,這表明Cu-DCA晶格是拓撲非平庸的.從邊界的局域態密度,可以清楚地看到與體帶邊緣連接的非平庸的拓撲邊界態,如圖4(f)所示.

為了更好地了解Cu-DCA晶格的內在拓撲特性,進一步分析了電子計數和軌道雜化.根據上述計算結果,費米能級附近的Kagome能帶主要來自Cu-DCA晶格中DCA分子的pz軌道.即可以將DCA分子視為外殼層中具有兩組孤對電子對的超原子,并且傾向于從其最近鄰的Cu原子接受電子.Cu原子和DCA分子之間的軌道雜化示意圖如圖5(a)所示,每個箭頭表示具有上或下自旋的一個電子,而每個黑點表示兩個自旋簡并的電子.Cu原子的d軌道(dxz和dyz)與DCA分子氰基的孤對電子(π軌道)之間的雜化形成四組三重態:成鍵態t1,t2和反鍵態 t?1,t?2.Cu-DCA 晶格的原胞中共有14個價電子參與軌道雜化,兩個來自Cu原子(Cu的其他價電子占據其余d和s軌道不參與雜化),12個來自DCA分子氰基的孤對電子.因此,t1和t2能帶被完全占據,另外兩個電子填充由t?1形成的狄拉克帶的下半部分,使得費米能級精確地位于忽略自旋軌道耦合的狄拉克點處或者是考慮自旋軌道耦合的帶隙中.

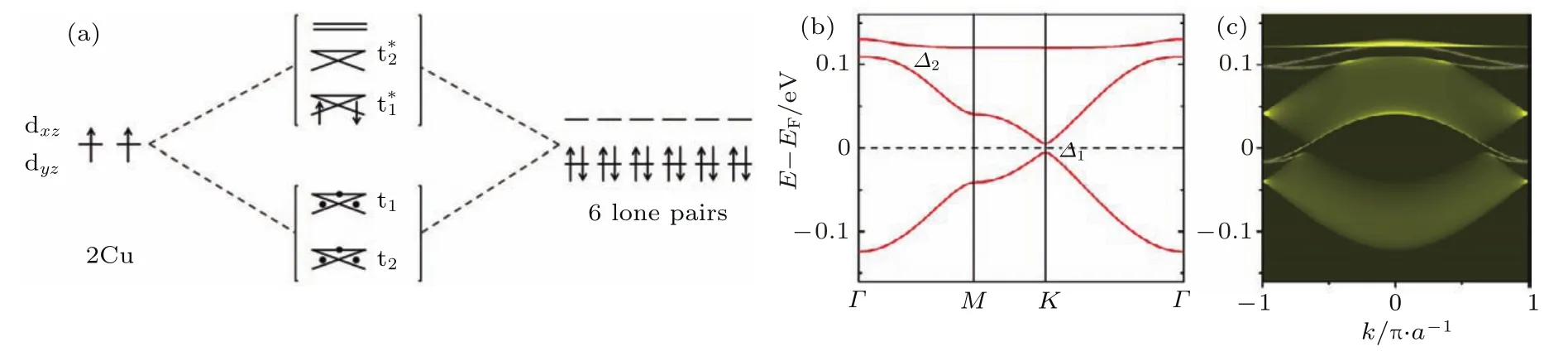
圖5 二維Cu-DCA的軌道雜化示意圖和Au-DCA晶格的電子性質[55](a)Cu原子與DCA分子中氰基的孤對電子對之間的軌道雜化示意圖,每個箭頭表示自旋向上或向下的一個電子,而每個黑點表示兩個自旋簡并的電子;(b)考慮自旋軌道耦合后Au-DCA薄膜的能帶結構;(c)自旋軌道耦合帶隙內的半無限狄拉克邊界態Fig.5 . of the orbital hybridization of Cu-DCA lattice and electronic properties of Au-DCA lattice[55]:(a)Orbital hybridization between Cu atoms and the lone pairs from the CN groups of DCA molecule,each arrow denotes one electron with an up or down spin,while each black dot denotes two spin-degenerate electrons;(b)band structure with SOC and(c)the semi-inf i nite edge states within the SOC gaps of Au-DCA.

通過前面電子計數與軌道雜化分析,可以預測具有貴金屬與氰基配位的類似結構的二維有機材料也應該是本征拓撲絕緣體.這種金屬-氰基的配位結構在金屬有機框架中廣泛存在.實驗上也多次報導過貴金屬或過渡金屬與氰基有配位作用,例如兩重和三重配位的Cu—NC鍵[56,57,61,62],三重配位的Au—NC鍵[63],三重和四重配位的Co—NC鍵[47,64],兩重配位的Fe—NC和Ni—NC鍵[57]等,因此有許多與Cu-DCA晶格相似的結構可以通過多種實驗手段進行合成.用Au原子替換Cu-DCA中的Cu原子構成了Au-DCA晶格.在圖5(b)和圖5(c)中展示了考慮自旋軌道耦合的能帶以及非平庸的拓撲邊界態.Au-DCA和Cu-DCA晶格的能帶結構和拓撲性質都非常相似,并且Au-DCA晶格具有更大的自旋軌道耦合帶隙.

5 總結與展望

目前理論上已經預測了一系列的二維有機拓撲絕緣體,但是一般二維有機薄膜均生長在金屬襯底上,由于金屬有機晶格與金屬襯底的相互作用很強,材料的拓撲性質會被基底覆蓋,因此減弱金屬有機晶格與金屬襯底之間的相互作用已成為未來發展的核心問題.本研究領域的另一個挑戰是目前合成的二維金屬有機材料尺寸太小,一般在納米尺度,不適合用來測量晶體材料的拓撲性質.值得強調的是2017年11月Liljeroth團隊[58]在外延石墨烯襯底上合成出了Co與有機分子配位形成的金屬有機結構,削弱了金屬襯底對材料內稟屬性的影響,為測量材料的拓撲性質提供了一條新的途徑.從2013年二維有機拓撲絕緣體發現至今,這類材料還處于研究的初級階段,進一步的深入研究為實驗上合成二維有機拓撲絕緣體以及構建三維有機拓撲絕緣體提供了新的思路.

特別感謝美國猶他大學Feng Liu教授,感謝中國科學院物理研究所陶蕾博士、金鑫和張現利對文章寫作的建議.