探測器對量子增強馬赫-曾德爾干涉儀相位測量靈敏度的影響?

李詩宇 田劍鋒 楊晨 左冠華 張玉馳 張天才?

1)(山西大學光電研究所,量子光學與光量子器件國家重點實驗室,極端光學協同創新中心,太原 030006)

2)(山西大學物理電子工程學院,太原 030006)

(2018年6月19日收到;2018年10月8日收到修改稿)

1 引 言

相位的精密測量是物理學領域中的重要內容,提高干涉儀相位測量的靈敏度和準確度,一直是人們不懈追求的目標.作為性能優異的相干光源,激光已被廣泛應用于精密測量領域.采用相干光源的干涉儀相位測量靈敏度可以達到經典極限,該極限由真空漲落決定的標準量子極限[1]確定.利用了高質量、高強度相干光源的光學干涉儀已經實現了引力波探測[2].早在20世紀80年代,Caves[1]提出了利用壓縮真空態注入馬赫-曾德爾干涉儀,可以獲得超越標準量子極限的相位測量靈敏度并獲得了實驗驗證[3,4].1993年,Holland和Burnett[5]證明了在無振幅差噪聲的情況下,利用孿雙數態注入馬赫-曾德爾干涉儀可以實現海森伯極限的相位靈敏測量.1998年,Kim等[6]提出利用孿雙數態注入干涉儀,結合光強差漲落測量或符合計數測量,可以達到海森伯極限的靈敏測量.2003年,Campos等[7]提出利用宇稱探測也可以實現海森伯極限的測量.2007年,Higgins等[8]結合單光子數態、自適應測量和反饋控制,可以精確地測量未知相位的大小,且靈敏度超越標準量子極限.2010年,Anisimov等[9]提出利用雙模壓縮真空態結合宇稱探測,實現海森伯極限靈敏度的測量.2011年,Seshadreesan等[10]將相干態和壓縮真空態按相同的光強比例混合注入干涉儀,利用宇稱探測達到海森伯極限的靈敏測量.2014年,我們也提出了利用光子數態、壓縮真空態結合光子數可分辨探測和宇稱探測等手段,有效提高法布里-珀羅干涉儀的分辨率和靈敏度的方案,實現超越標準量子極限的量子增強測量[11].除了壓縮態、孿雙數態以外,人們發現糾纏態也可以用于量子增強的超靈敏測量中[12].2007年,Nagata等[13]利用四光子糾纏的NOON態和后選擇測量,在實驗上實現了打破標準量子極限的超分辨相位估計.2010年,Gerry和Mimih[14]利用雙相干態結合宇稱探測實現了海森伯極限的靈敏測量.2011年,Joo等[15]利用糾纏相干態結合宇稱探測達到海森伯極限的靈敏測量.

上述工作中,人們通常假定探測過程是理想的,忽略了環境中的噪聲對系統的影響.而實際過程中的傳輸損耗、相位擴散、非理想的探測器都會不同程度減弱量子增強的效果.1999年,Kim等[16]分析了在非理想探測下,基于孿雙數態的符合計數測量對相位靈敏度的影響,發現不同的探測效率下最佳測量角不同,且被測相位在一定范圍內可以打破標準量子極限.2008年,Gilbert等[17]分析了在干涉儀中存在損耗時基于NOON態的投影測量對相位靈敏度的影響,發現微小的損耗也會導致相位估計精度的急劇變差,甚至無法達到標準量子極限.2011年,Genoni等[18]分析了相位擴散下的相位估計問題,利用量子Fisher信息對相移高斯態的測量精度極限進行了評估,發現在很寬的噪聲范圍內,零差檢測幾乎是最優的檢測方案.2012年,Genoni等[19]提出了一種可以控制相位擴散的干涉方案,實驗證明了在大相位擴散下,相干態優于壓縮態而成為最佳選擇,零差檢測和相干信號幾乎是檢測相移的最佳方法.2011年,Datta等[20]分析了孿雙數態注入干涉儀中,輸入狀態、損耗和檢測器效率對相位靈敏度量子增強效果的影響,發現損耗影響比較小,而輸入狀態的制備效率和檢測器效率的影響比較大.2012年,Xie和Peng[21]分析了干涉儀中光子損耗對壓縮疊加態注入干涉儀時相位靈敏度的影響,發現隨著損耗的增大,小壓縮下比大壓縮下靈敏度增大的速度要快得多.2016年,華東師范大學研究小組[22]在理論和實驗上研究了SU(1,1)干涉儀中光場的衰減和吸收損耗對量子噪聲的影響,得到的結論是干涉儀中不同的損耗對輸出光場量子噪聲的影響不同,在某些情況下量子噪聲對損耗不敏感,幾乎不受損耗的影響.2017年,Xie和Chen[23]又分析了振幅阻尼、比特-相位翻轉這兩種量子噪聲對相干態、壓縮真空態、自旋壓縮態注入干涉儀時相位靈敏度的影響,發現靈敏度隨著振幅阻尼噪聲的增大而增大,甚至無法達到標準量子極限,而相干態注入干涉儀的靈敏度不受比特-相位翻轉噪聲的影響,壓縮真空態、自旋壓縮態注入干涉儀的靈敏度隨著比特-相位翻轉噪聲的增大先增大后減小,且在大多數情況下,自旋壓縮態比其他兩種情況注入干涉儀時的增大速度快.

我們看到,損耗對不同量子資源和不同探測策略的影響不同.盡管人們已就光子數態和壓縮態對于相位測量靈敏度的量子增強作用進行了討論[24],但損耗對相位測量靈敏度的影響針對某些特定量子態尚未研究.本文研究了非理想的探測效率,對采用光子數態、關聯數態、壓縮真空態三種量子光源注入的馬赫-曾德爾干涉儀相位測量靈敏度的影響,獲得了相位測量靈敏度與探測器量子效率的定量關系.研究表明,當光子數態注入時,相位測量靈敏度始終不能超越標準量子極限;當關聯數態注入時,探測效率不得小于75%才可以超越標準量子極限,獲得相位測量的量子增強;對于壓縮真空態,只要有壓縮光注入,就可以實現相位測量的量子增強;相位靈敏度皆隨探測效率增大而不同程度的提高,壓縮真空態比關聯數態具有更好的量子增強效果.本文給出了量子增強的精密測量實驗對探測效率的要求,這對結合實際系統進行量子增強測量的研究具有重要意義.

2 馬赫-曾德爾干涉儀模型

馬赫-曾德爾干涉儀的基本模型如圖1所示.其中BS1和BS2是兩個無損且對稱的50:50的光學分束器,M1和M2是兩個全反鏡,1和2分別為馬赫-曾德爾干涉儀的入射端口,入射光場通過分束器BS1后沿著上下兩條路徑傳播,經過分束器BS2后,被輸出端的兩個光電探測器所探測.通過分析探測器所輸出的光電流強度即可得到干涉儀兩條路徑間的相位信息.其中上下兩條路徑的相移分別為θ3和θ4,相位差θ=θ4?θ3.光學分束器在光學研究中是一種應用廣泛且很重要的線性光學器件.在海森伯繪景下光場的湮滅算符與相應的共軛產生算符滿足玻色對易關系[25]:馬赫-曾德爾干涉儀輸出端光場的湮滅算符滿足關系式:

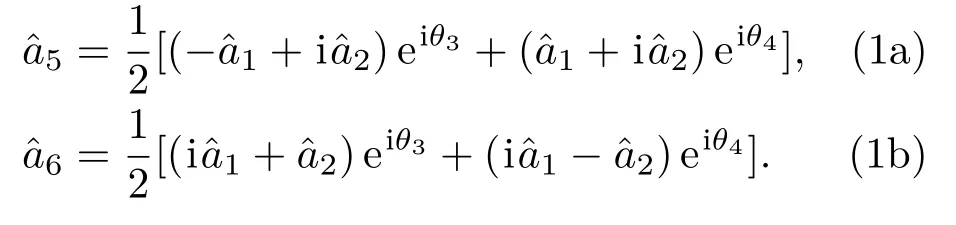
圖1 馬赫-曾德爾干涉儀的基本模型Fig.1 .Mach-Zehnder interferometer.

在研究馬赫-曾德爾干涉儀模型時,可以將其看成是一個SU(2)群的線性裝置,其角動量算符的Schwinger表達式為[25]:

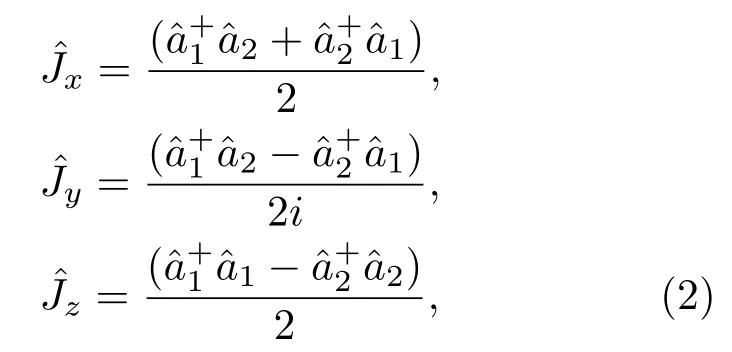
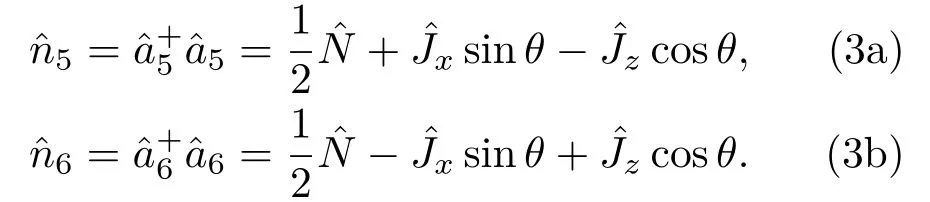
利用光強差測量方案研究馬赫-曾德爾干涉儀的相位測量靈敏度,設光強差測量算符滿足關系式根據誤差傳遞公式得到相位測量靈敏度?θ,可由(4)式確定[26]:

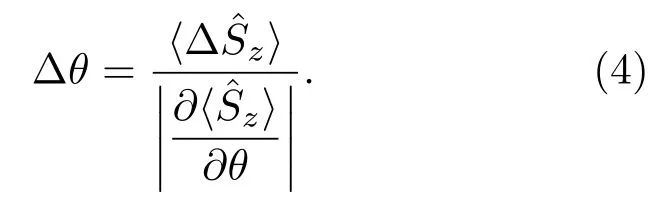
3 理論分析

實驗中,測量儀器不可能是理想的,探測器量子效率小于1[27].非理想探測會影響相位測量的靈敏度[16,20].本文分析了當光子數態、關聯數態、壓縮真空態分別注入馬赫-曾德爾干涉儀時,探測器量子效率對相位測量靈敏度的影響,其中相干光場作為本底光作為信號放大作用出現.假設光電探測器量子效率為η,則在探測器處被探測到的光場模式的湮滅算符滿足關系式:其中和分別為光場進入探測器時輸入模式和真空模式的湮滅算符.為了便于計算,假設在馬赫-曾德爾干涉儀兩個輸出口探測器量子效率都為η,則在干涉儀的兩個輸出端口處探測器對輸出光場的湮滅算符分別表示為實際探測到的平均光子數為

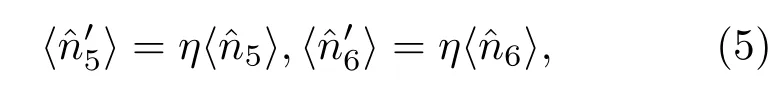
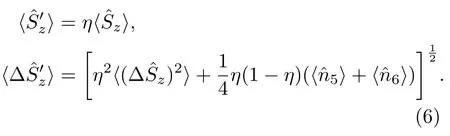
3.1 光子數態注入

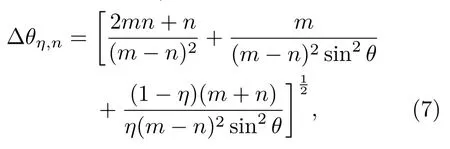
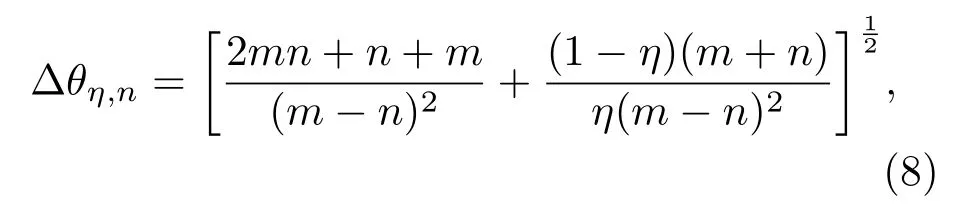
此時θ為最優測量相位.當η=1時,得到理想情況下的相位測量靈敏度為

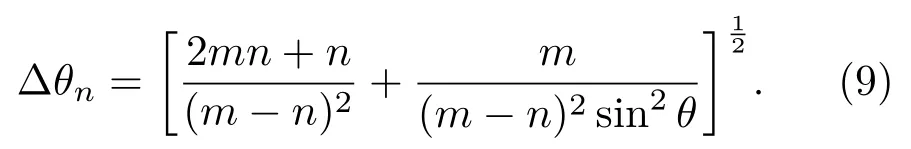
另外,當入射的光子數態和相干態的平均光子數相等時,即m=n時,根據海森伯數相不確定關系?n?θ>1[28]可知,當?n=0,無論量子效率是多少,相位靈敏度發散為無窮大,即?θ→∞,此時不適合量子相位靈敏度測量.

下面分析η=1時被測相位的靈敏度如何隨數態光子數的變化.假設入射相干態的平均光子數m=1000,則測量相位在最優處時,歸一化相位測量靈敏度如圖2所示.可知數態的注入使得靈敏度降低,其中n=0表示只有相干態(m=1000)注入,歸一化相位測量靈敏度等于1,此時靈敏度最小,而隨著光子數的增加,對應的歸一化標準量子極限為1.因此光子數態和相干態同時注入到干涉儀時,并不能超越標準量子極限.這與數態的性質一致,因為數態具有最穩定的振幅,其相位起伏最大,不利于相位的測量.

圖2 歸一化相位測量靈敏度隨數態光子數的變化Fig.2 .Normalized phase measurement sensitivity as the number of photons.

3.2 關聯數態注入

早在1986年,Yurke等[25]就提出過可以構造一種關聯數態注入馬赫-曾德爾干涉儀,實現相位測量的靈敏度接近海森伯極限.考慮這樣一種入射態:

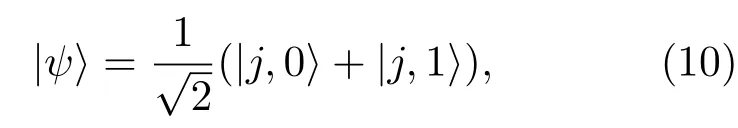
由此可知當測量相位在最優處時有sinθ=0,最佳靈敏度為

當η=1時,得理想情況下的相位測量靈敏度為[25]

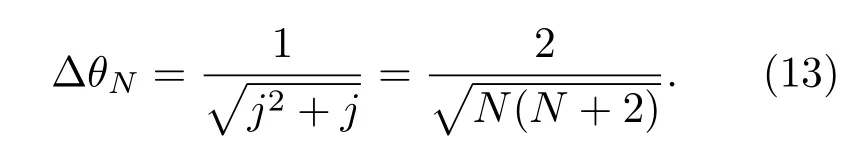
當N ? 1時,靈敏度?θ～ 2/N,接近海森伯極限. 為了實現量子增強,對探測器量子效率有一定的要求. 當?θη,N< ?θη,SQL時,為存在損耗時的標準量子極限,即

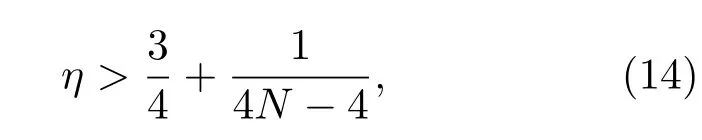
由此可知,N ? 2時,η>75%,即探測器量子效率必須大于75%才可以實現相位測量的量子增強.

3.3 壓縮真空態注入

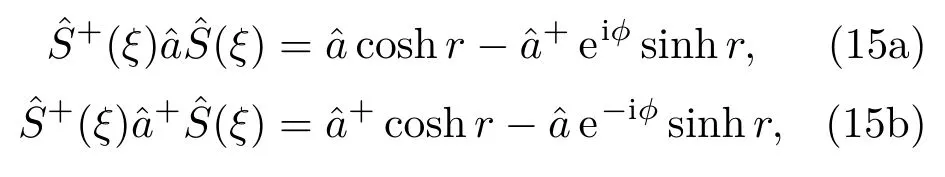
利用光強差探測方案得到在探測器量子效率為η時,相位測量靈敏度為

當η=1時,得到理想情況下我們熟知的相位測量靈敏度[24]

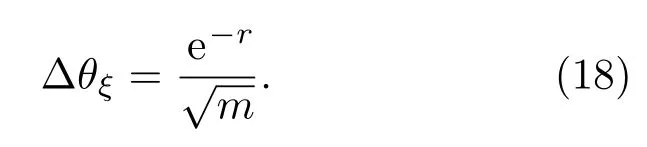
該靈敏度超越了標準量子極限.考慮探測不理想情況下,要實現量子增強需滿足?θη,ξ<是存在損耗時的標準量子極限,即

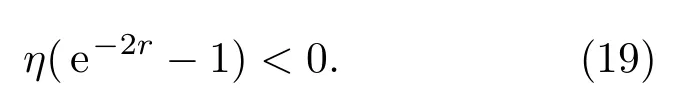
因為e?2r<1,所以(19)式恒成立,即只要有壓縮光注入,原則上只要探測效率不為0,就總是可以實現一定程度的量子增強.

4 結果與討論

1999年,Kim等[16]討論了探測器效率對孿雙數態注入馬赫-曾德爾干涉儀相位靈敏度的影響,得到的結論是相位角在很小的范圍內可實現量子增強,并且存在一個最優的相位角,隨著探測效率的增大,獲得量子增強的相位角的范圍也變大,在不同的探測效率下,最優相位角也不同.而探測效率對于關聯數態、壓縮真空態注入的馬赫-曾德爾干涉儀相位靈敏度的影響之前沒有討論過.在這里我們進一步分析關聯數態、壓縮真空態注入馬赫-曾德爾干涉儀,探測器量子效率η對相位測量靈敏度的影響.將相位測量靈敏度歸一化到標準量子極限.為了討論的一致性,利用壓縮度s和平均光子數的關系得到和壓縮度對應的平均光子數,將壓縮度采用平均光子數進行描述.這樣我們就可以得到關聯數態、壓縮真空態注入馬赫-曾德爾干涉儀,當測量相位處于最優處,歸一化相位測量靈敏度隨探測器效率的變化,結果如圖3所示.圖3(a)為不同光子數(4,6,8,10,100)下的結果.光子數4,100對應的線和標準量子極限(黑色虛線)的交點對應的效率分別為83.33%,75.25%,對應于該條件下獲得量子增強所需要的最小探測效率;隨著光子數的增大,需要的最低探測效率逐步降低,直到最低要求的量子效率75%.圖3(b)為壓縮真空態注入的結果.由此可以看出,靈敏度都隨探測效率的增加而不同程度地提高.比較而言,相同能量下,壓縮真空態的相位測量靈敏度比關聯數態更加超越標準量子極限,顯示了壓縮真空態具有更好的量子增強效果.

為了進一步比較關聯數態、壓縮真空態注入干涉儀的量子增強受探測效率的影響,我們定義量子增強參數p為歸一化到標準量子極限的相位測量靈敏度的負對數值.這樣定義的量子增強參數p是大于零的實數,值越大量子增強越大.根據該定義,得到對應關聯數態和壓縮真空態注入時的量子增強參數pN和pξ分別為

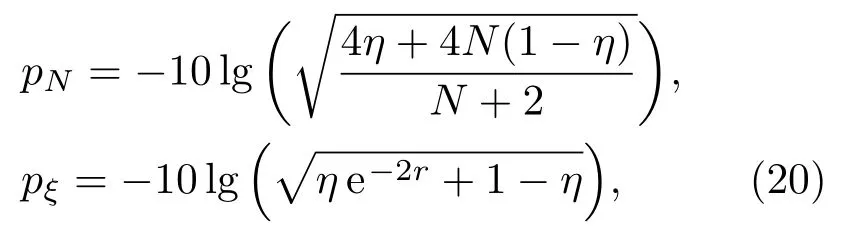
兩種狀態對應的量子增強比為rp=pξ/pN.如果rp>1,壓縮真空態獲得的量子增強大;如果rp<1,關聯數態獲得的量子增強大.圖4為關聯數態、壓縮真空態注入干涉儀,當測量相位處于最優處的量子增強比較.從圖4可以看到,rp總是大于1,說明壓縮真空態所獲得的量子增強總是比關聯數態大.關聯數態在光子數4,6,8,10,20,100時,實現量子增強所需最小探測器量子效率分別為83.33%,80%,78.57%,77.78%,76.32%,75.25%.另外當關聯數態光子數為2,需要探測器量子效率為1才能實現量子增強;基于以上分析可知,當探測器量子效率和平均光子數都相同時,壓縮真空態比關聯數態注入馬赫-曾德爾干涉儀所獲得的量子增強效果更好.

圖3 相位測量靈敏度隨探測效率的變化 (a)關聯數態注入的結果;(b)壓縮真空態注入的結果Fig.3 .Phase sensitivity as a function of detection quantum efficiency:(a)Results of correlated Fockstate injection;(b)results of squeezed vacuum state injection.

圖4 關聯數態、壓縮真空態注入干涉儀的量子增強比較(虛線對應的值等于1)Fig.4 .Comparison of the quantum enhancement for correlated Fock-state,squeezed vacuum state injection(The black dotted line is equal to 1).

前面我們討論了探測效率對壓縮態和相干態注入到馬赫-曾德爾干涉儀中相位靈敏度的影響.這一結果可以應用到引力波探測系統中,探測效率的提高可以提高引力波探測器的靈敏度.在GEO 600[29,30]引力波探測中,利用高質量、高強度的相干光和壓縮光注入到邁克耳孫干涉儀,演示了探測靈敏度的增強.當考慮探測效率時,引力波探測的靈敏度為

式中

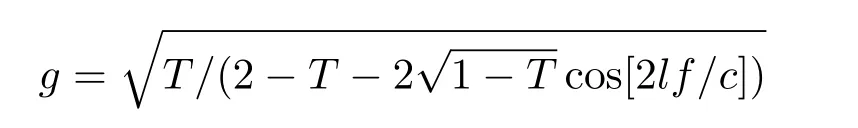
為信號放大因子,T為信號回收鏡的功率透射率;λ,P和c分別為入射的相干光的波長、功率和波速,l為干涉儀的臂長;f是由于引力波通過干涉儀而引起反射鏡振蕩的頻率.根據GEO 600[29]引力波探測中提供的參數:T=1.9%,λ=1064 nm,P=3.7 kW,c=3×108m/s,l=1200 m,當壓縮光是16 dB時,e?2r=0.025.η是光功率輸入到輸出的傳輸系數,可等效為我們討論的干涉儀系統中的探測效率;1?η是總損耗的累積,包括光的散射、吸收、模式失配、光探測等,可等效為探測的總損耗.當頻率低于100 Hz時量子輻射壓力噪聲(quantum radiation pressure noise)為主要噪聲,當頻率高于100 Hz時散粒噪聲為主要噪聲[30,31].本系統是在打破散粒噪聲情況下分析的,所以考慮頻率高于100 Hz的情形.圖5為在頻率為300—5000 Hz時,引力波探測器的靈敏度隨探測效率的變化曲線,當探測效率提高時,引力波探測器的靈敏度也提高了.

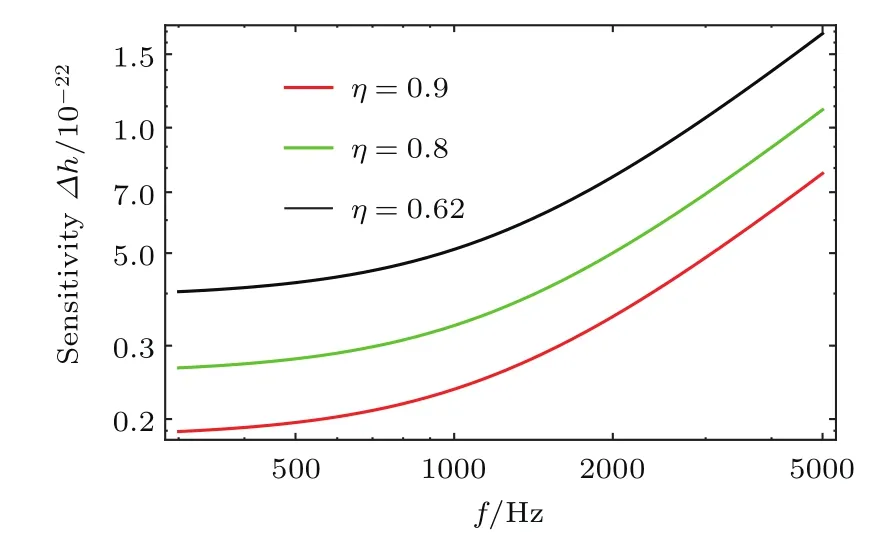
圖5 引力波探測器的靈敏度隨探測效率的變化Fig.5 .Sensitivity of gravitational-wave detector versus detection efficiency.

5 結 論

本文研究了強度差測量方案下,探測效率對光子數態、關聯數態、壓縮真空態三種量子光源注入馬赫-曾德爾干涉儀相位測量靈敏度的影響.研究表明:光子數態注入時,相位測量靈敏度始終不能超越標準量子極限;對于關聯數態的注入,要獲得相位測量的量子增強效應,探測器量子效率不得小于75%;對于壓縮真空態,只要存在壓縮,原則上就可以實現量子增強.無論何種情況,相位測量靈敏度皆隨探測器的量子效率增大而不同程度的提高,且在相同的探測效率和平均光子數下,壓縮真空態比關聯數態所獲得的量子增強效果要好.一般情況下,探測效率對量子增強有顯著影響,而這種影響與量子資源和測量策略有關.這項研究針對壓縮真空等已經在實驗上產生的優質量子資源和常用的馬赫-曾德爾干涉儀,因此所得到的結論具有一定的代表性,使我們認識到實現量子增強必須對探測器提出相應的要求.這對人們在實際應用中,比如引力波的探測,希望通過馬赫-曾德爾干涉儀實現相位靈敏度超越標準量子極限的測量,具有重要的指導意義.