考慮晶粒分布的多晶體材料超聲散射統一理論?

李珊 李雄兵 宋永鋒? 陳超

1)(中南大學交通運輸工程學院,長沙 410075)

2)(中南大學粉末冶金國家重點實驗室,長沙 410083)

(2018年9月22日收到;2018年10月11日收到修改稿)

1 引 言

超聲波在多晶體材料中傳播時,鄰近晶粒的取向差引起晶界處的聲阻抗變化,最終導致超聲波的散射[1].由于散射的發生,超聲波能量將隨著傳播距離的增加而衰減,其相速度也將發生色散[2].O’Donnell等[3]研究表明只有準確地對超聲散射過程進行正演建模,才能實現材料力學性能或微觀結構的超聲散射反演評價.

相關研究最早由Mason和McSkimin提出[4,5],Huntington[6]和Papadakis[7]在此基礎上構建了著名的超聲散射分區近似模型.該模型為分段解析解,根據波數k和平均晶粒直徑ˉd來對頻域進行劃分:當kˉd?1時,為瑞利(Rayleigh)散射區;當kˉd≈1時,為隨機(Stochastic)散射區;當kˉd?1時,為幾何(Geometric)散射區.但該模型難以統一描述全頻域范圍的散射情況,且無法給出確切的散射區轉換點(或函數分段點).Weaver[8]基于Dyson方程和Born近似,用自由能算子推導了衰減譜.然而該方法僅適用于瑞利散射區和隨機散射區,且無法得到相速度譜.Calvet和Margerin[9,10]利用Dyson方程及譜函數法推導了全頻域范圍內的衰減譜和相速度譜.但該方法屬于數值解,且運算中涉及到瑕積分,因此求解效率低,同時其精度受瑕積分數值解的影響大.Stanke和Kino[11]基于Keller近似,建立了超聲散射統一理論模型,用統一的數學形式來描述不同散射區的衰減和相速度變化,其結果為半解析解,求解效率高于譜函數法.由于該理論框架具有很強的普適性,隨后Hirsekorn[12]將Stanke和Kino的統一理論模型推廣到了多相材料.Ahmed和Thompson[13]又針對拉長晶材料,修正了統一理論模型中描述微觀組織的空間相關函數.

然而,Stanke和Kino的超聲散射統一理論僅使用平均晶粒尺寸來推導衰減譜和相速度譜,是不盡合理的.眾多研究表明超聲散射不僅與平均晶粒尺寸有關,而且與晶粒尺寸的分布有關[14?17].Smith[18]發現平均晶粒尺寸相同但晶粒尺寸分布不同的樣本衰減譜存在明顯差異.陳堯等[19]基于電子背散射衍射(electron backscattering dif f raction,EBSD)技術,對離心鑄造奧氏體不銹鋼構建了含晶粒分布的二維虛擬試塊,并用有限差分法得到了各向異性粗晶材料的衰減譜,但未給出相速度譜.Ryzy等[20]根據三維泰森多邊形虛擬了不同晶粒分布的試塊,運用有限元方法模擬發現,各向異性鎳合金的晶粒分布同時影響衰減譜及相速度譜.但有限元模擬的計算量大,且無法顯式表達衰減譜和相速度譜.Arguelles和Turner[21]使用對數正態分布方法描述晶粒尺寸分布,修正了空間相關函數,并得到了瑞利散射區衰減譜的解析解.然而該方法不適用于隨機散射區和幾何散射區,且無法計算相速度譜.此外,用對數正態分布來描述晶粒尺寸的分布,理論上假設了存在無窮大的晶粒,與實際不符,而且無窮大的晶粒會導致計算中的無窮積分而無法求解.

本文引入截斷對數正態分布描述晶粒分布的特性[22],推導了含晶粒分布修正的超聲散射統一理論模型,然后使用奧氏體304不銹鋼制備試塊,開展EBSD實驗和超聲散射實驗,驗證了修正模型的有效性.

2 理論模型

2.1 廣義的超聲散射統一理論

首先,假設由不同尺寸晶粒組成的單相多晶體金屬材料的密度均勻,但局部模量存在差異,則單相不均勻介質的線性彈性波波動方程可表達為[11]

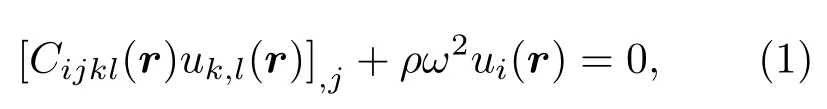
其中Cijkl(r)為世界坐標系下的局部彈性模量,ui(r)為質點位移場,ρ為多晶體金屬材料的密度,ω為彈性波的角頻率.記(1)式為L(r)u(r)=0,其中L(r)為一個作用于u(r)的不均勻介質波動方程算子,根據微擾理論有[12]

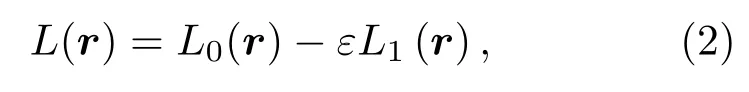
其中L0(r)為零階的均勻介質波動方程算子,而L1(r)則為一階的擾動算子,ε為一個遠小于1的無量綱量.零階和一階算子作用于質點位移場可以分別寫為[12]

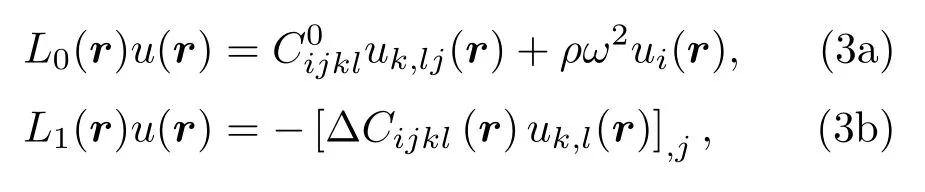
其中局部彈性模量Cijkl(r)被分解為一個宏觀均勻的各向同性介質彈性模量,以及一個擾動量?Cijkl(r)=Cijkl(r)?,其中可用Voigt平均方法得到.

接著,通過零階和一階算子構建波動方程的二階Keller近似,可得到質點的平均位移場〈u(r)〉為[12]

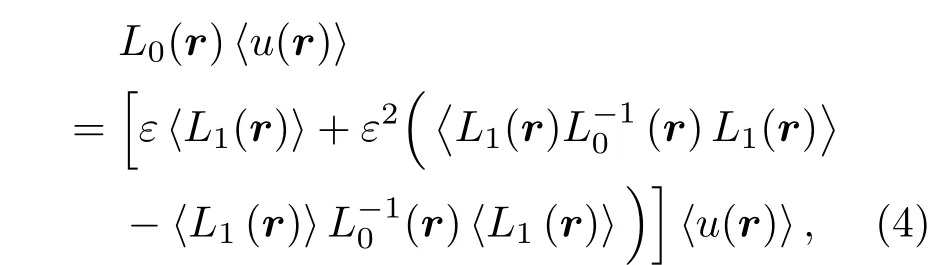
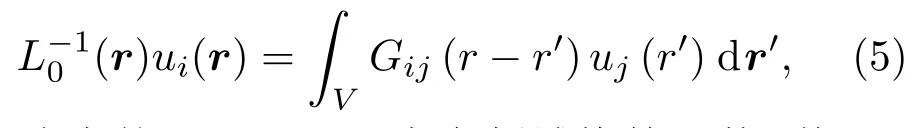
(5)式中的Gij(r?r′)為全頻域格林函數,其Lifshits和Parkhomovskii表達為[11]:

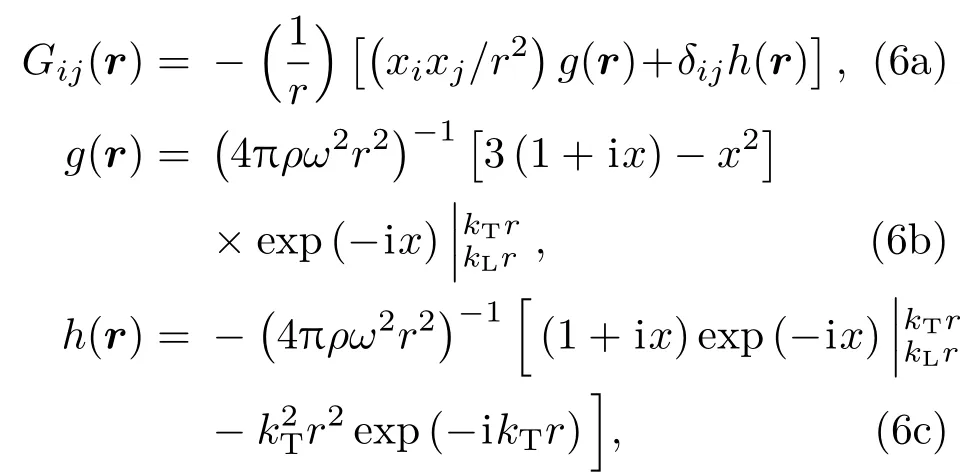
其中δij為Kronecker函數,kξ(ξ=L,T)為多晶體金屬的縱波和橫波復波數.因此將(3a)式、(3b)式和(5)式代入(4)式可得[11]

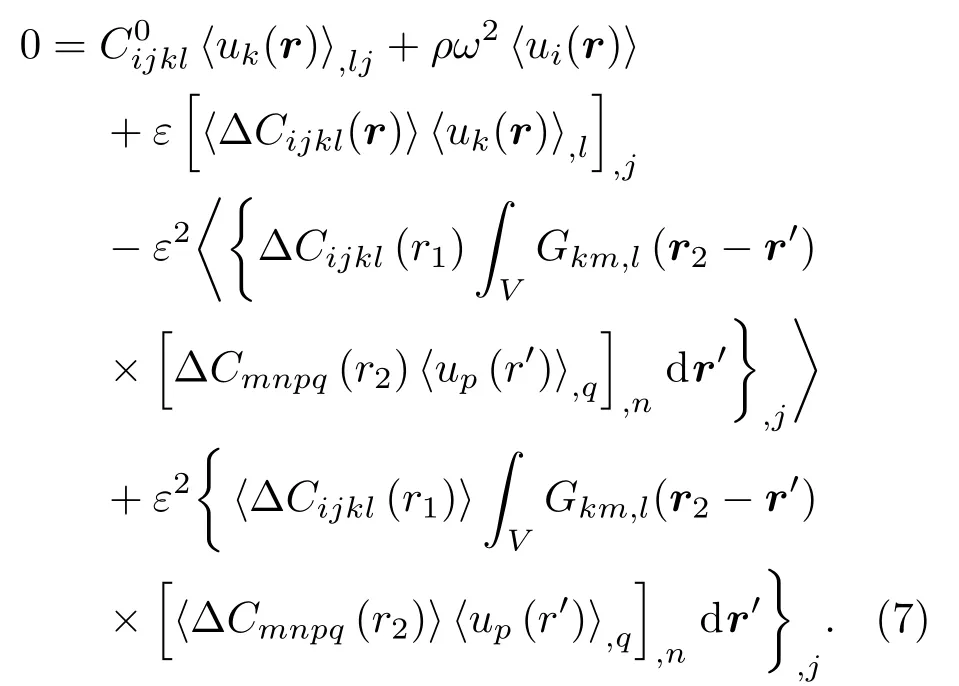
考慮多晶體金屬材料在局部上是不均勻的,但全局上具有統計均勻性,即一階晶粒統計量和二階晶粒統計量都與空間無關,則(7)式可以進一步化簡為[11]

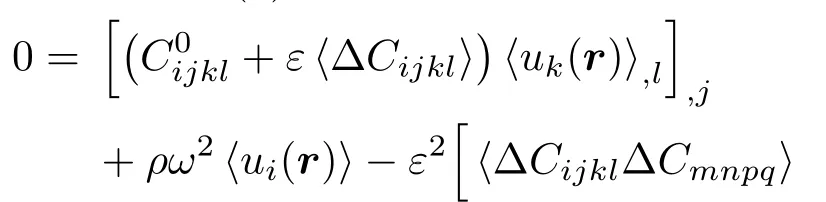
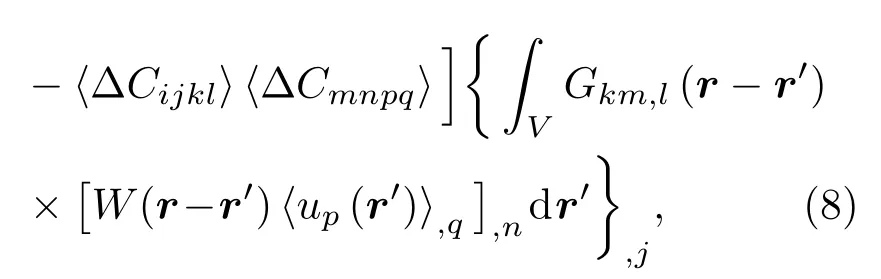
其中W(r?r′)為多晶體金屬材料的空間相關函數,用于描述空間點r和點r′落在同一個晶粒內部的概率.不失一般性,用平面波計算質點位移場為[11]

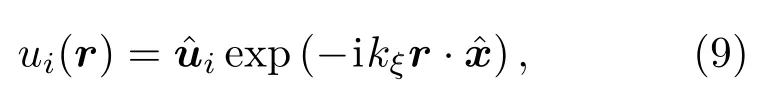
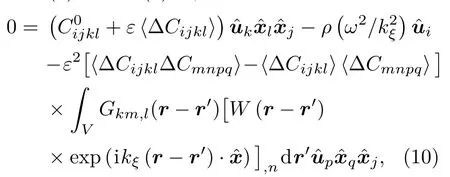
由格林第一公式可知[11]

其中S為體積分區域V的表面.當忽略側壁干擾時,(11)式中的面積分項可忽略.此時,將(11)式代入(10)式,令r′為原點得[11]

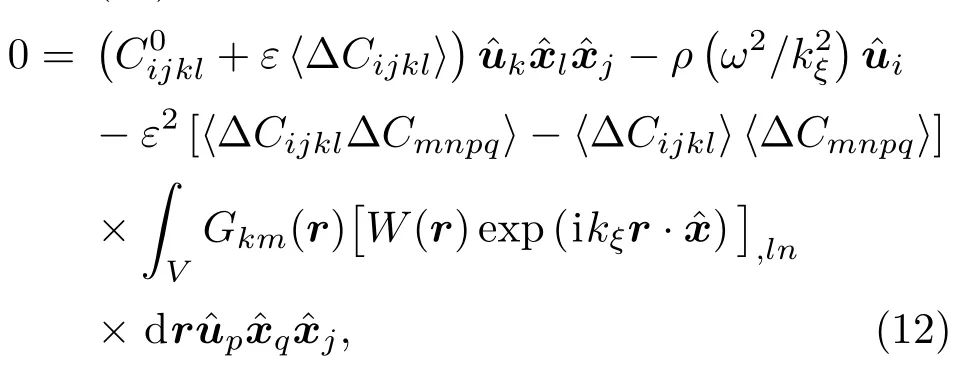
(12)式為超聲散射統一理論的廣義表達式.當單相多晶體具有任意對稱性、拉長晶、或織構時,(12)式都普遍適用(不適用于多相材料).

2.2 含晶粒分布的超聲散射統一理論

多晶材料主要可分為單相材料和多相材料.為了簡化問題本文將研究對象限定為單相材料,而且其晶格為面心立方對稱結構,不含織構,晶粒為球狀晶.假設晶粒尺寸具有分布特性,由于不含有織構且為球狀晶,因此(12)式可以化簡為[11]

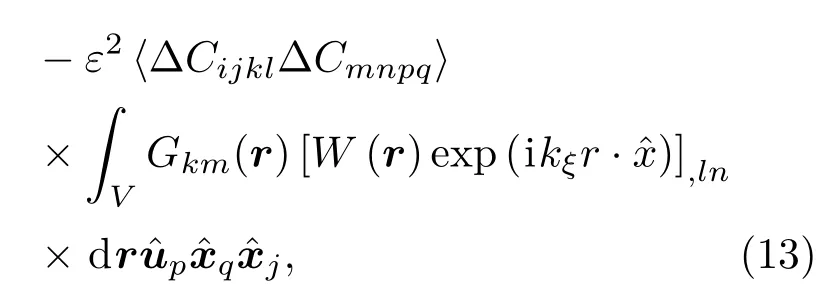
不考慮晶粒尺寸分布特性時,空間相關函數為W(r)=exp(?|r|/l),其中l為空間相關長度,實際上也就是晶粒的半徑.但本文考慮晶粒的半徑呈截斷對數正態分布[22],其概率密度函數為

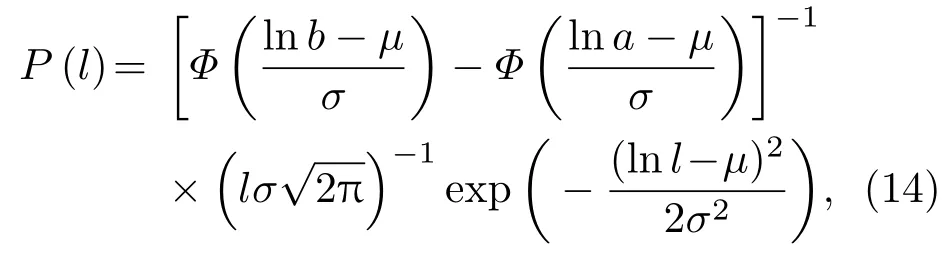
其中μ為位置參數,σ為尺度參數,a為下截斷點,b

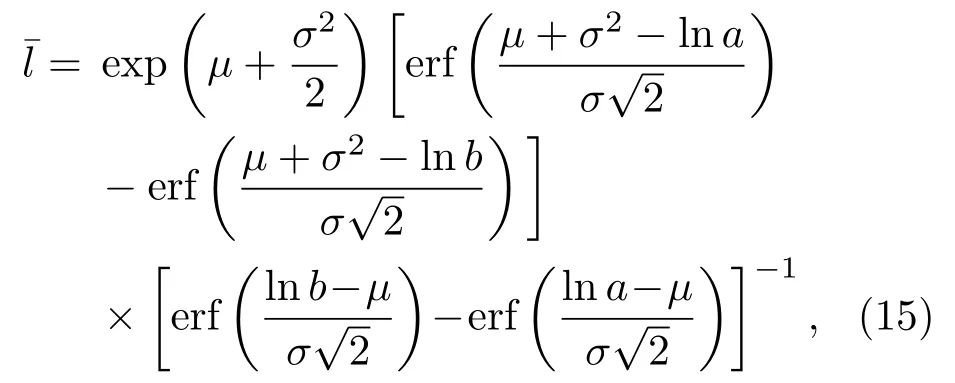
根據截斷對數正態分布可構造加權的空間相關函數為

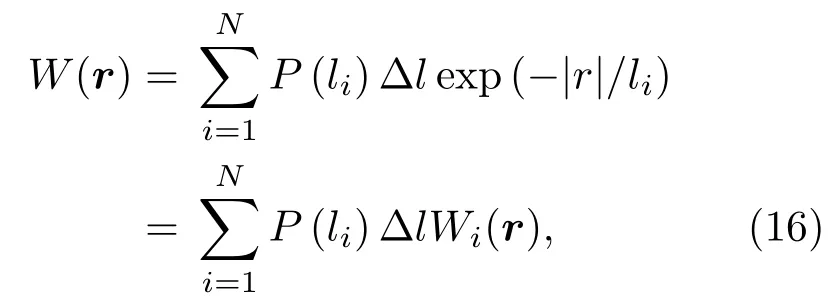
其中 li=a+(b? a)(2i? 1)/(2N),i=1,2,···,N,?l=(b?a)/N,N為晶粒分布區間被劃分的段數.注意到,在計算中N應足夠大且?l足夠小,使得定義e為給定的區間離散精度.將(16)式代入(13)式,可得到晶粒尺寸服從截斷對數正態分布時的超聲散射統一理論模型

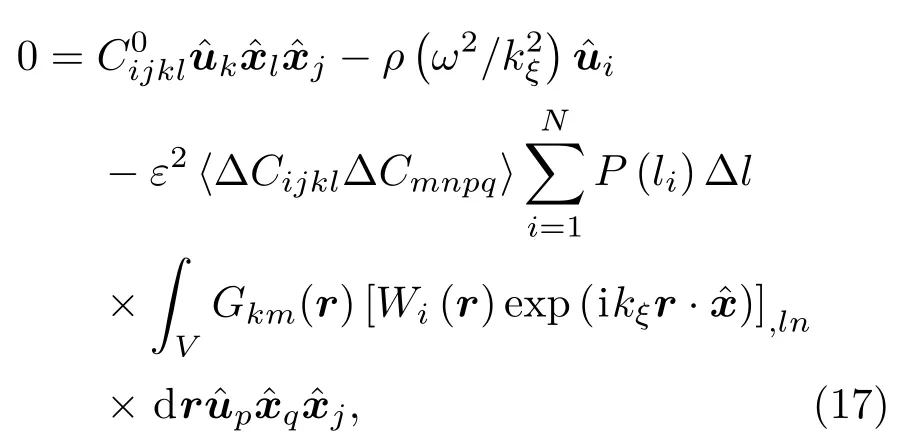
(17)式是本文的一個主要成果. 接著,結合Stanke和Kino[11]給出的彈性模量協方差張量可對(17)式進行求解,假設縱波和橫波都沿著x3方向傳播,其中橫波的偏振方向為x1方向,可得縱波和橫波的復波數分別為:

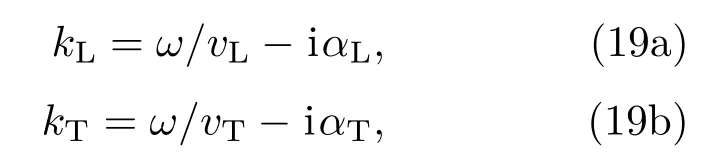
其中vL= ω/Re(kL)和vT= ω/Re(kT)分別為縱波和橫波的相速度,αL= ?Im(kL)和αT=?Im(kT)分別為縱波和橫波的衰減系數.通過(18a)式和(18b)式即可計算不同頻點下的衰減系數和相速度,即衰減譜和相速度譜.因此,問題的關鍵是如何對(18a)式和(18b)式進行有效的求解.本文擬使用迭代方法[2,23]對其進行計算,但由于(18a)式和(18b)式屬于復雜的非線性超越方程,迭代時對初值的選擇極為敏感.因此,引入超聲散射的分區近似模型,用理論近似解作為迭代初值,以實現超聲散射統一理論模型的快速求解.

Stanke和Kino基于不含晶粒分布的超聲散射統一理論,已經推導了在瑞利散射區、隨機散射區和幾何散射區下的復波數近似模型.當考慮晶粒分布時,本文通過截斷對數正態分布函數,構造加權平均得到近似模型.因此,對于縱波,近似模型分別為:

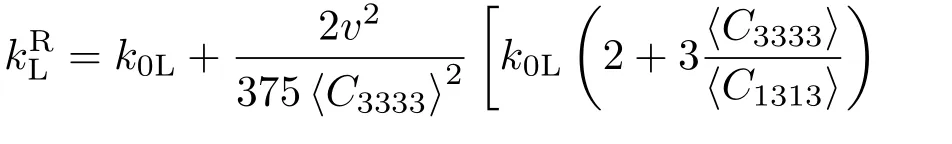
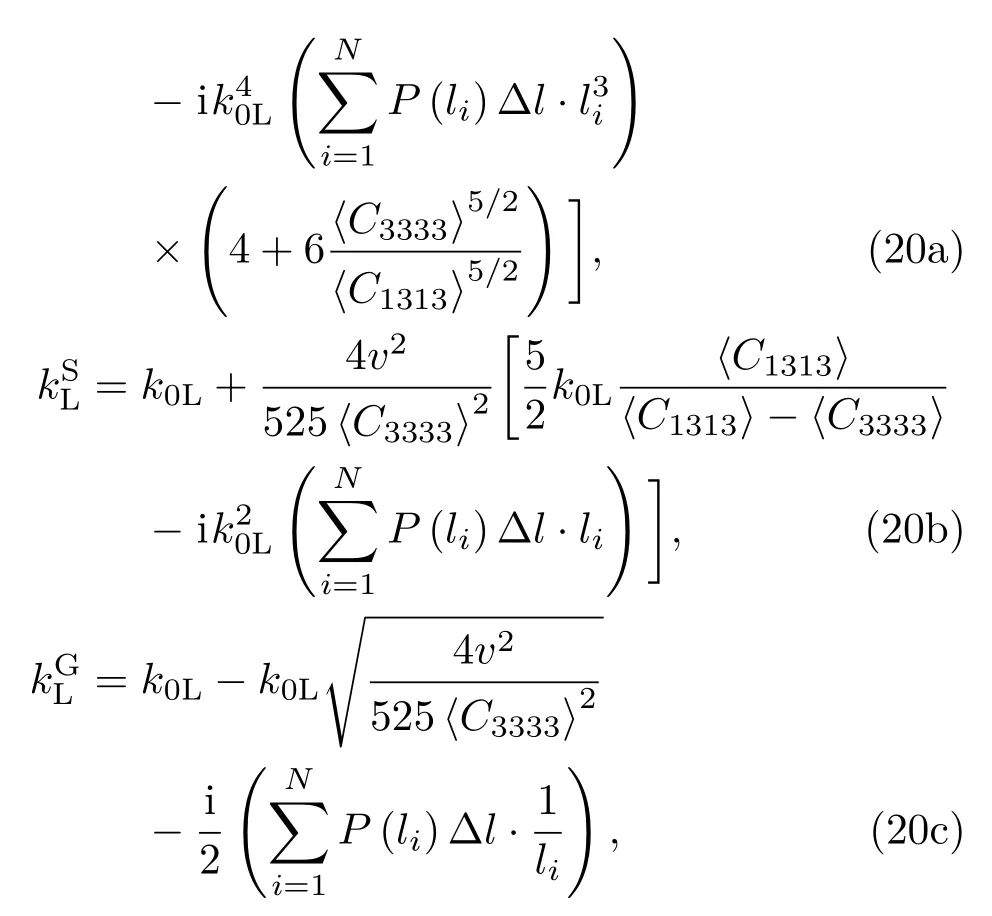
而對于橫波有

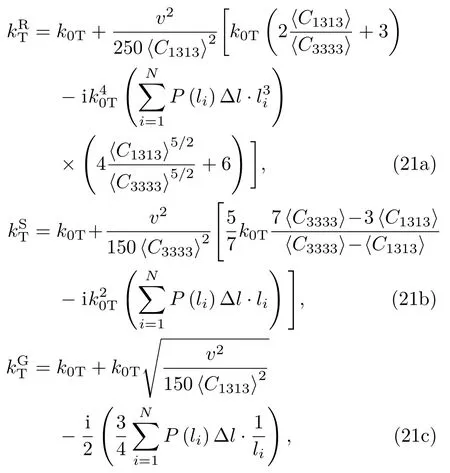
其中,上標R,S,和G分別代表著瑞利(Rayleigh)散射區、隨機(Stochastic)散射區和幾何(Geometric)散射區. 當歸一化頻率為0<2k0ξˉl 6 10?1時,本文以瑞利散射區為(18a)式和(18b)式的迭代求解初值;當歸一化頻率為10?1<2k0ξˉl 6 101時,以隨機散射區為初值;當歸一化頻率為2k0ξˉl>101時,則以幾何散射區為初值.

2.3 數值結果分析

為揭示晶粒分布對衰減譜和相速度譜的影響,取具有相同數學期望值的截斷對數正態分布進行對比,其中選取晶粒半徑的下截斷點為a=10μm,上截斷點為b=120μm,平均晶粒半徑為ˉl=25μm. 選取尺度參數分別為σ=0.25,0.5,0.75,1,則從(15)式可知相應的位置參數,從而得到概率密度分布函數圖,如圖1所示.顯然,截斷對數正態分布僅在l∈[10,120]μm的范圍內有意義,在該范圍外被成功地截斷,通過積分進行檢驗,結果等于1.當尺度參數越小時,晶粒半徑的分布越集中,且概率密度的峰值約接近于設定的數學期望值.當尺度參數越大時,例如σ=1時,截斷的作用和效果越明顯,同時驗證了截斷對數正態分布可表現出近似于指數分布的特性[17].而當σ→0時,即不考慮晶粒分布的情況.另一方面,在進行區間離散時,本文給定晶粒分布區間的離散精度為e=10?3.

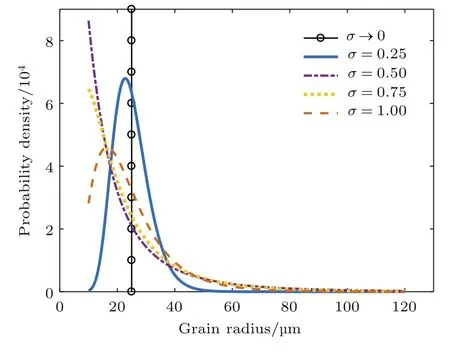
圖1 晶粒半徑的概率密度分布Fig.1 .Grain size distributions with a constant mean=25 μm and varying scale parameter σ.

以圖1所代表的5種晶粒分布為基礎,研究不同分布作用下的縱波和橫波的衰減譜和相速度譜.假設本文所選用的單相不銹鋼材料的密度為ρ=7930 kg/m3,并分別設定其3個獨立的單晶彈性常數為:c11=204.6 GPa,c12=137.7 GPa,c44=126.2 GPa[24]. 同時,c33=c22=c11,c23=c13=c12,c66=c55=c44,其他單晶彈性常數均為0.各向異性系數上述單晶彈性常數的下標采用Voigt記法:11→ 1,22→ 2,33→ 3,23→4,13→5,12→6.根據一階晶粒統計量的Voigt平均有:

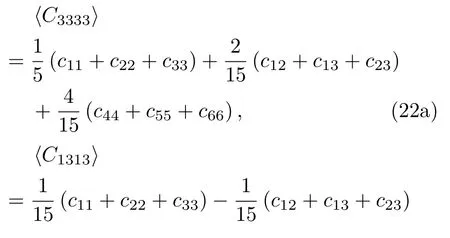
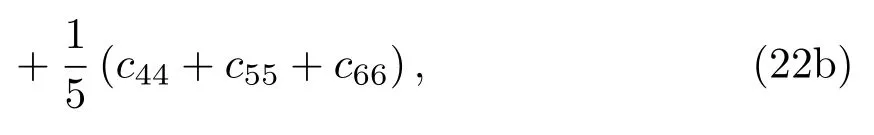
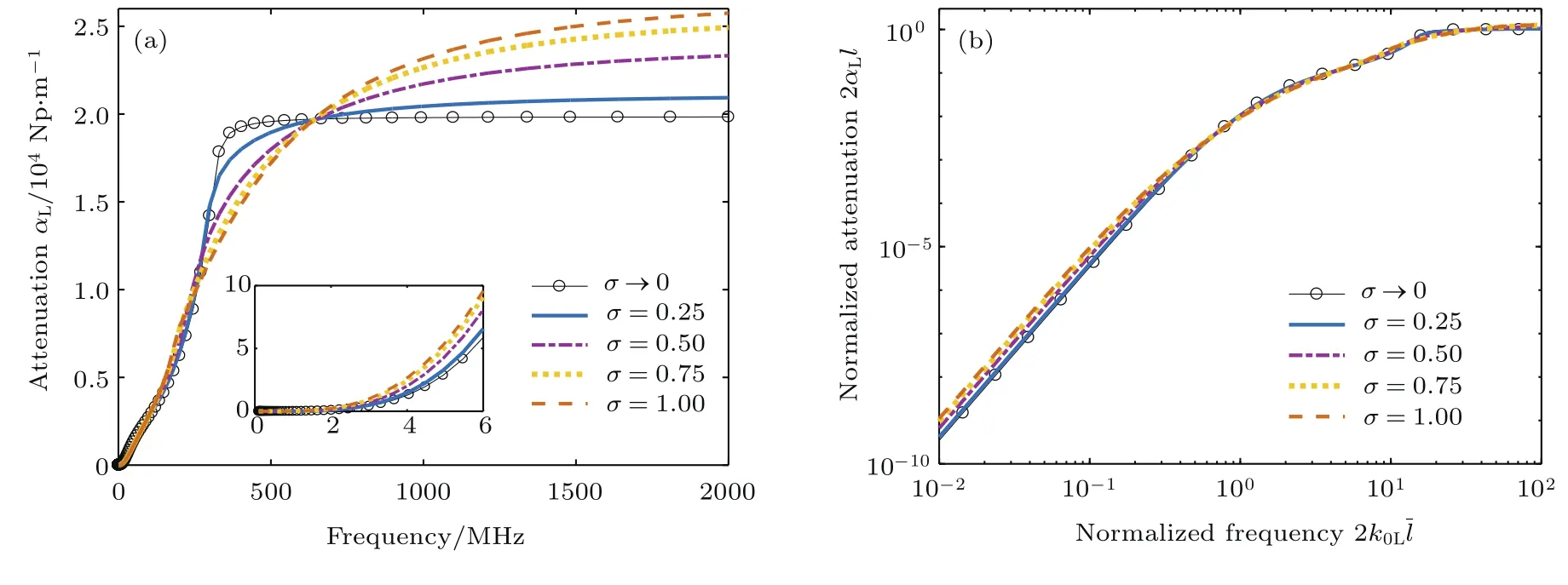
圖2 不同晶粒分布下的縱波衰減譜 (a)衰減-頻率圖;(b)歸一化衰減-歸一化頻率圖(雙對數坐標圖)Fig.2 .Attenuation spectrums of longitudinal wave using dif f erent grain size distributions:(a)Attenuation-frequency graph;(b)normalized attenuation-normalized frequency graph(log-log plot).

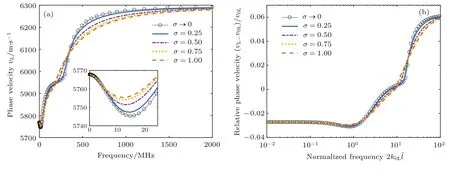
圖3 不同晶粒分布下的縱波相速度譜 (a)相速度-頻率圖;(b)相對相速度-歸一化頻率圖(雙對數坐標圖)Fig.3 .Phase velocity spectrums of longitudinal wave using dif f erent grain size distributions:(a)Phase velocityfrequency graph;(b)relative phase velocity-normalized frequency graph(log-log plot).

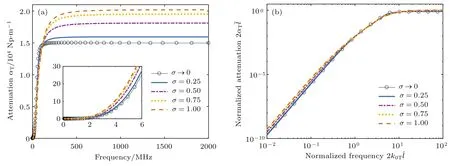
圖4 不同晶粒分布下的橫波衰減譜 (a)衰減-頻率圖;(b)歸一化衰減-歸一化頻率圖(雙對數坐標圖)Fig.4 .Attenuation spectrums of transverse wave using dif f erent grain size distributions:(a)Attenuation-frequency graph;(b)normalized attenuation-normalized frequency graph(log-log plot).

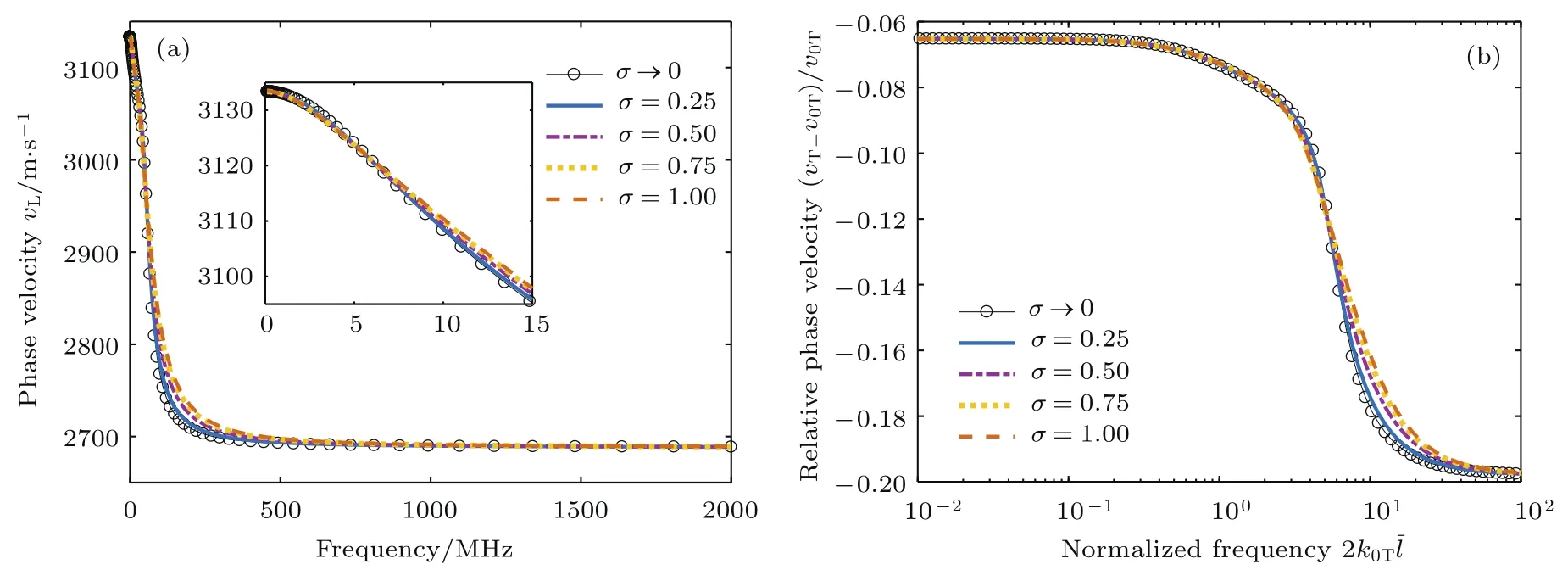
圖5 不同晶粒分布下的橫波相速度譜 (a)相速度-頻率圖;(b)相對相速度-歸一化頻率圖(雙對數坐標圖)Fig.5 .Phase velocity spectrums of transverse wave using dif f erent grain size distributions:(a)Phase velocityfrequency graph;(b)relative phase velocity-normalized frequency graph(log-log plot).

圖6 超聲散射分區近似模型和統一理論模型的對比 (a)縱波衰減;(b)縱波相速度;(c)橫波衰減;(d)橫波相速度Fig.6 .Comparison between the asymptotic model and the unif i ed theory model for ultrasonic scattering:(a)Longitudinal wave,attenuation;(b)longitudinal wave,phase velocity;(c)transverse wave,attenuation;(d)transverse wave,phase velocity.

最后,以σ=1時的晶粒分布為例,比較超聲散射的分區近似模型和統一理論模型,結果如圖6所示.可明顯看出,分區近似模型是離散的,尤其是相速度譜不連續,在不同的散射區之間沒有交點.而在精度方面,瑞利散射區和幾何散射區的近似精度較高,誤差主要存在于隨機散射區及其兩個相鄰的轉換區.因此,研究統一理論模型是有必要的,結果在全頻域上可連續,而分區近似模型作為近似解,作為統一理論模型迭代求解的初值也是合適的.

3 實驗系統及測量結果

本文實驗采用304不銹鋼材料對理論模型進行驗證.首先對一個304不銹鋼坯料進行線切割加工,得到一個外形尺寸為40 mm × 40 mm ×25 mm的超聲實驗試塊,并在其相鄰位置切割出三個5 mm× 5 mm× 5 mm的金相實驗樣品,假設超聲實驗試塊和金相樣的微觀組織在統計意義下完全一致.對試塊和金相樣的表面分別用砂紙打磨至1000目,并用尼龍布及0.3μm的拋光液進行拋光至鏡面效果.

本文使用EBSD技術對材料進行金相分析[25],確定晶粒尺寸的分布.首先,對金相樣進行鑲樣,利用Buehler VibroMet 2型振動拋光機對金相樣進行3 h的振動拋光,用FEI Quanta 650 FEG型場發射掃描電鏡和NordlysMax2 EBSD探測器對金相樣進行晶粒尺寸測定.共測試5個視場,其中一個測試結果如圖7所示,5次測試中標定率最低為95.47%.通過5領域外插法對EBSD圖像進行降噪去除非真實的小晶粒,可以降低標定率對平均晶粒尺寸的影響.使用HKL CHANNEL5軟件包提供的晶粒重構算法可以直接算出平均晶粒尺寸,并給出各個晶粒的具體分布情況,其中臨界的晶界角度取向差為10?,將晶粒取向差在10?以內的孿晶合并成一個晶粒進行分析,并通過將符合60?〈111〉關系的孿晶界完全除去,對平均晶粒尺寸進一步修正為直徑48.2μm.每個正交面分別觀察3個視場,最終用EBSD測量得到平均的晶粒半徑為ˉl=24.1μm,而晶粒半徑最小值為10.0μm,最大值為125.5μm.故選取晶粒半徑的下截斷點為a=10.0μm,上截斷點為b=125.5μm.基于最小二乘法,調整位置參數和尺度參數,對5個視場EBSD得到的晶粒半徑頻率分布立方圖進行擬合.截斷對數正態分布擬合歸一化結果如圖7(b)所示,當μ≈?13.581且σ≈1.563時,擬合優度為99.2%.

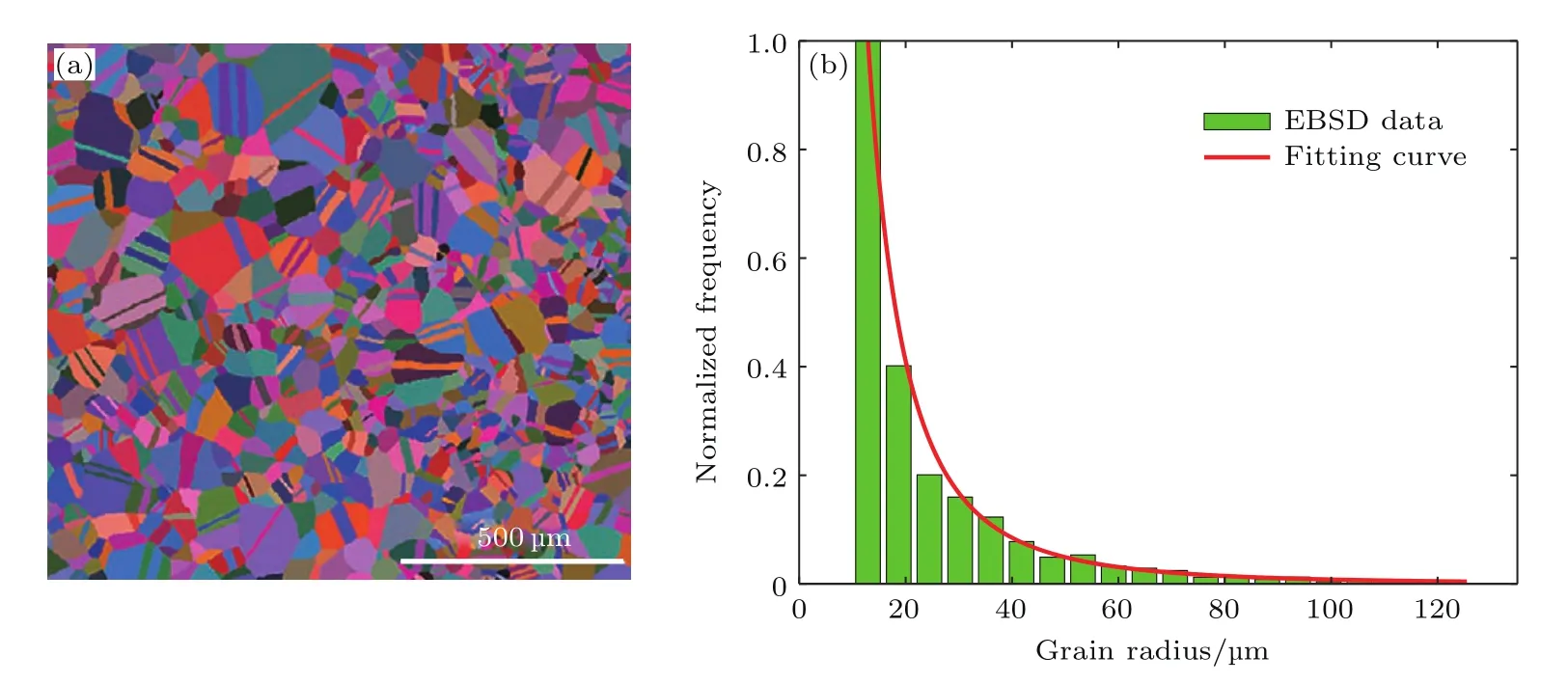
圖7 304不銹鋼金相樣的EBSD測量結果 (a)降噪后的取向成像圖;(b)晶粒半徑分布Fig.7 .The EBSD measurement results of the 304 stainless steel specimen:(a)The orientation imaging of the samples after denoising;(b)the grain size distribution.

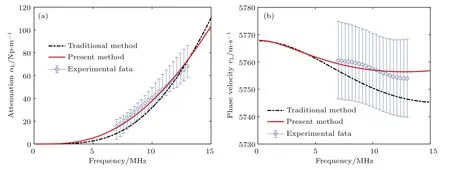
圖8 縱波散射實驗結果(a)衰減譜;(b)相速度譜Fig.8 .The experimental results of the longitudinal wave scattering:(a)Attenuation spectrum;(b)phase velocity spectrum.

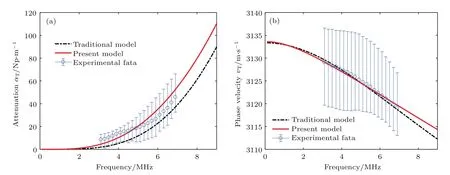
圖9 橫波散射實驗結果(a)衰減譜;(b)相速度譜Fig.9 .The experimental results of the transverse wave scattering:(a)Attenuation spectrum;(b)phase velocity spectrum.

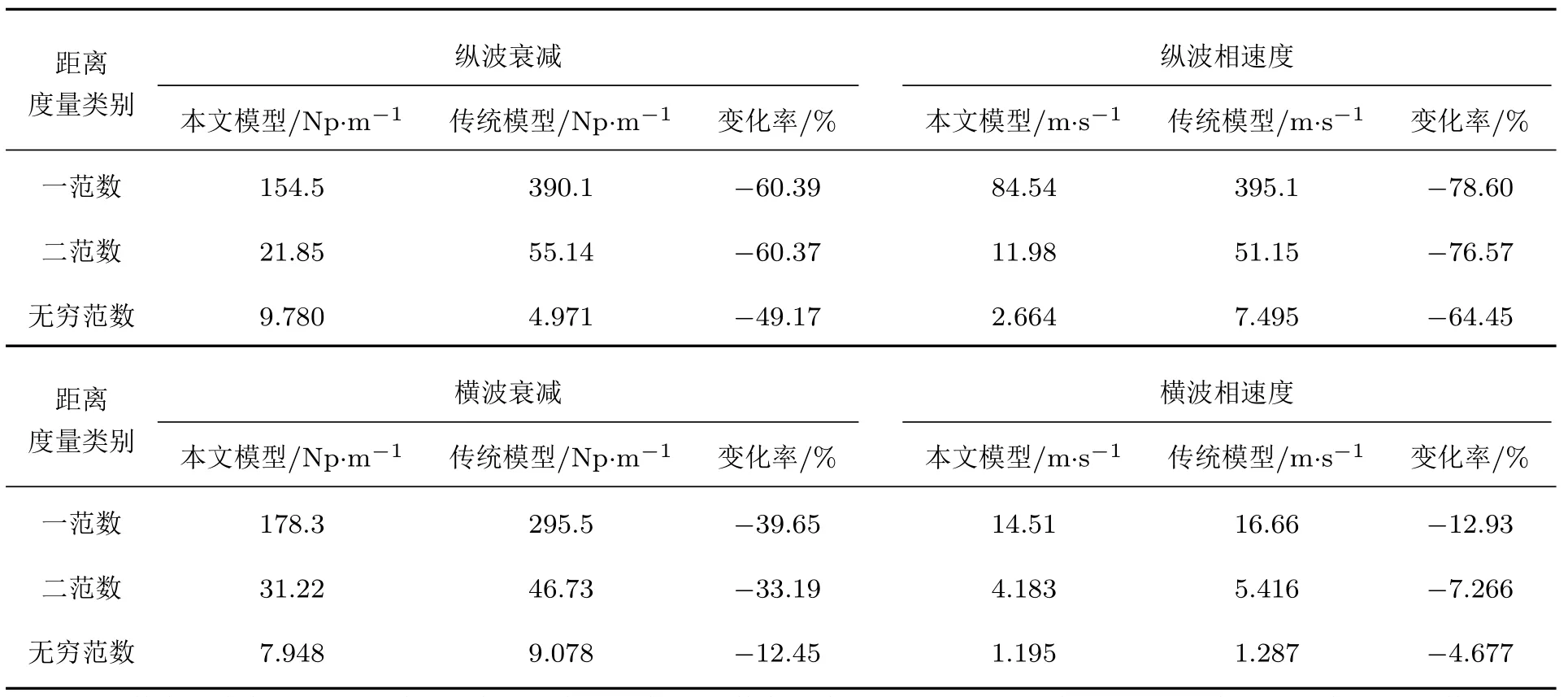
表1 實驗結果與模型計算值之間相異性度量結果Table 1 .The measures of dissimilarities between experimental data and theoretical model.

由于水浸法難以測量橫波衰減,本文采用接觸式脈沖反射法進行縱波和橫波的實驗.超聲信號采集系統主要由JSR Ultrasonics的DPR300型超聲脈沖發生/接收器,ADLink的PCIe-9852型高速數字采集卡,以及不同的超聲接觸式探頭構成.考慮到幾何散射區的衰減過大,導致難以在實驗中采集到超聲回波,本文選用Olympus的V111-RM型10 MHz縱波直探頭,和V155-RB型5 MHz橫波直探頭,開展超聲衰減譜和相速度譜測量實驗[26].10 MHz縱波和5 MHz橫波的頻段正好處于瑞利散射和隨機散射的轉換區(2k0Lˉl=0.511,2k0Tˉl=0.452),可同時對兩個散射區進行驗證.縱波衰減譜和相速度譜的實驗結果如圖8所示,而橫波衰減譜和相速度譜的實驗結果如圖9所示,圖中實驗測量結果僅顯示探頭有效帶寬部分.對相異性度量進行計算,得到不同范數意義下的距離比較,結果如表1所示.可見,考慮晶粒分布特性對超聲散射統一理論模型進行修正后,衰減譜和相速度譜測量結果和理論模型之間的相異性存在不同程度的降低.其中,縱波衰減譜和相速度譜的符合程度提高得尤為明顯.

4 討 論

從以下四個方面對考慮晶粒分布特性的多晶體金屬超聲散射統一理論進行分析和討論.

首先,選用截斷對數正態分布取代傳統的對數正態分布來描述多晶體金屬的晶粒分布特性,使晶粒分布模型具有了實際的物理意義,避免了晶粒尺寸為零,或為無窮大的情況出現.而且通過EBSD的金相分析方法,確定了晶粒分布的上界和下界,繼而惟一確定了晶粒的截斷對數正態分布,這也證明了本方法在物理上是可行的.

第二,應注意到本文的(18a)式、(18b)式和Hirsekorn所給出的多相材料超聲散射統一理論模型在數學形式上是等價的(見文獻[12]中(14)式和(15)式).Hirsekorn的模型是每個晶粒的物相不同,但尺寸相同,根據相含量進行加權.而本文模型是每個晶粒的尺寸不同,但物相相同,根據晶粒分布進行加權.其中蘊含的物理意義是:可認為具有同一物相、同一晶粒尺寸的晶粒的集合,是對超聲散射起作用的一組基本單元.

最后,從圖5(b)和圖9(b)可發現,橫波相速度在瑞利散射和隨機散射區受晶粒分布的影響相對較小,此物理特性可能應用于材料晶粒分布的超聲散射反演評價.其原因是,用橫波相速度估計平均晶粒尺寸后,晶粒分布獨立的參數只剩余三個,此時通過縱波衰減、縱波相速度、橫波衰減聯立求解剩余的三個參數,繼而可無損估計晶粒分布.

5 結 論

基于晶粒尺寸的截斷對數正態分布特性,推導了受晶粒分布影響的多晶體材料超聲散射統一理論.根據該理論模型,在平均晶粒尺寸一致的條件下,通過數值模擬方法分析了晶粒分布范圍擴大對固體內部超聲背散射的影響:1)對縱波及橫波衰減而言,在瑞利散射區衰減和幾何散射區的衰減明顯增大,而在隨機散射區及相鄰兩個轉換區衰減變化幅度較小;2)對縱波相速度而言,在隨機散射區及其與幾何散射的轉換區內有明顯的變化,而在其他散射區的變化較小;3)對橫波相速度而言,除了在隨機散射與幾何散射轉換區的變化明顯外,其他散射區變化較小.對于晶粒半徑在10.0—125.5μm范圍內變化的304不銹鋼試塊,實驗結果表明,晶粒分布修正后模型的精度高于傳統模型.其中,縱波衰減譜和相速度譜的精度有顯著的提高,和實驗結果間的一范數距離比傳統模型分別降低了約60%和79%.可見,僅使用平均晶粒尺寸建模,無法準確地計算衰減譜和相速度譜,有必要考慮晶粒分布進行修正.未來,本文模型可進一步擴展至含拉長晶粒、宏觀織構或多個物相的材料.