Rashba自旋軌道耦合下square-octagon晶格的拓撲相變?

楊圓1)2)? 陳帥1) 李小兵1)

1)(江蘇科技大學張家港校區,張家港 215600)

2)(南京大學,固體微結構物理國家重點實驗室,南京 210093)

(2018年4月9日收到;2018年10月2日收到修改稿)

1 引 言

拓撲絕緣體是一種新的量子物質態,其體電子態是有能隙的絕緣態,而其邊界或表面是無能隙的金屬態[1?5],這種金屬態是由能帶結構的拓撲性質決定的,受到時間反演對稱性的保護.量子自旋霍爾效應,即二維的拓撲絕緣體,是通過自旋軌道耦合來實現的,其拓撲性質可以由Z2不變量[6,7]或者自旋陳數[8?10]刻畫.對于時間反演對稱的電子系統,Z2指標和自旋陳數給出完全等價的描述.但是在時間反演對稱性被破壞的情況下,將無法定義Z2拓撲不變量,而自旋陳數的魯棒性依然保持不變[8].最近,自旋陳數被用于描述交換場作用下量子自旋霍爾效應的拓撲性質[11].研究結果發現,在時間反演對稱性被破壞后,量子自旋霍爾態的非平庸拓撲性質仍然存在.這種時間反演對稱破缺的量子自旋霍爾效應在弱無序情況下,其邊界上的螺旋邊緣態結構依然是穩定的.實驗上也在InAs/GaSb量子阱中證實了時間反演對稱性破缺的量子自旋霍爾效應的穩定性[12].

石墨烯的內稟自旋軌道耦合強度非常弱[13?15],而破壞鏡面對稱性的外稟Rashba自旋軌道耦合作用也不利于實現量子自旋霍爾效應[6].但是,在石墨烯中通過引入Rashba自旋軌道耦合和破壞時間反演對稱性的交換場,可以實現一種無朗道能級的量子霍爾效應,即量子反常霍爾效應[16,17].量子反常霍爾效應邊緣態具有手征的特征.當Rashba自旋軌道耦合和交換場同時存在時,人們在kagome晶格[18],star晶格[19]和Lieb[20]晶格中也發現了量子反常霍爾態.

在HgTe/CdTe量子阱中發現量子自旋霍爾效應之后,一些新的二維拓撲絕緣體也相繼被提出,比如kagome晶格[21]、修飾的蜂窩狀晶格[22]和單層銻異質結構等[23].近年來,square-octagon晶格憑借其獨特的幾何結構吸引了一些理論工作者的研究興趣,并得到了許多有意義的結果[24?30].例如,Kargarian和Fiete[24]研究了具有自旋軌道耦合的square-octagon晶格中的拓撲相;Bao等[26,27]利用團簇動力學平均場理論和連續時間量子蒙特卡羅算法,描述了溫度和相互作用對squareoctagon晶格中電子行為的影響.然而到目前為止,Rashba自旋軌道耦合作用和交換場對squareoctagon晶格的拓撲性質的影響還未被研究.另一方面,隨著實驗條件的改善和實驗技術的發展,二維蜂窩狀六角晶格[31]和kagome晶格[32]可以通過操縱光晶格中的超冷原子來構建,因此我們相信square-octagon晶格在不久的將來能夠在實驗中得以實現.特別的是,實驗上發現功能材料ZnO具有準square-octagon結構[33].因此,本文將研究各向同性square-octagon晶格在內稟自旋軌道耦合、Rashba自旋軌道耦合和交換場作用下的拓撲相變,本工作的研究能夠加深對square-octagon晶格以及準square-octagon結構材料的認識.

本文將證明考慮Rashba自旋軌道耦合作用和交換場時,各向同性square-octagon晶格也會支持量子自旋霍爾效應的存在,并且處于不同填充因子時可以實現不同的拓撲相.利用陳數和自旋陳數確定系統的拓撲性質,同時為了驗證各種拓撲相的存在,計算了square-octagon晶格的邊緣態能譜以及自旋性質.計算結果表明,在鏡面對稱性和時間反演對稱性都被破壞的情況下,量子自旋霍爾效應中邊緣態的能譜可以是無能隙的,而其對應的自旋譜存在著譜隙.進一步調節交換場的大小,系統會發生從螺旋邊緣態到自旋過濾的手征邊緣態的拓撲相變,這為自旋量子調控提供了一種新的思路.

2 模型和方法

2.1 緊束縛模型

本文考慮的晶格結構如圖1(a)所示.1,2,3,4表示一個原胞內的四個不等價原子,與其對應的第一布里淵區如圖1(b)所示,高對稱點為Γ,X和M,緊束縛哈密頓量可以表示為[1,6,24,30]

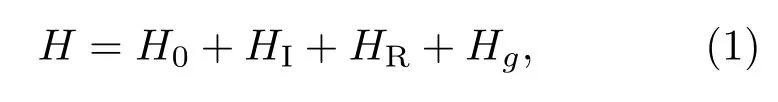
其中

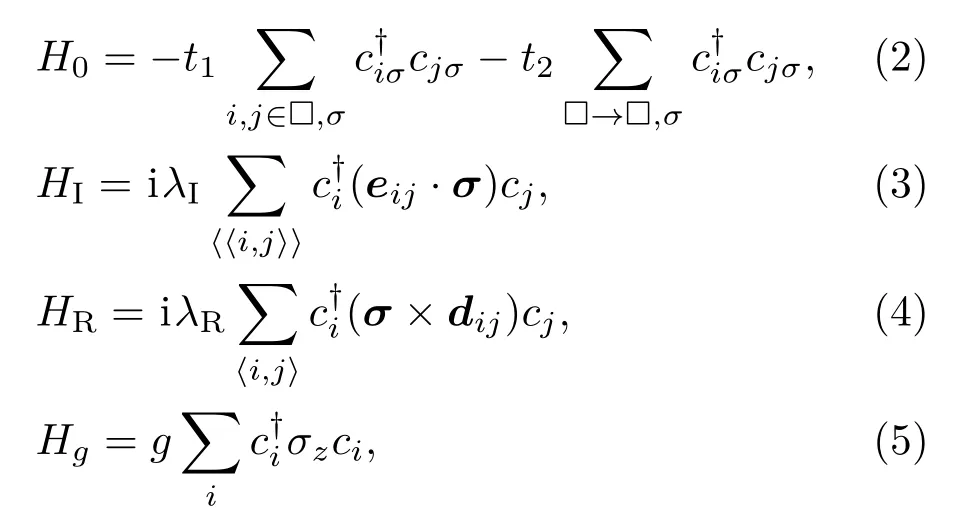
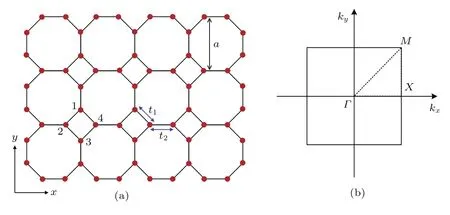
圖1 Square-octagon晶格 (a)結構示意圖;(b)第一布里淵區Fig.1 .Square-octagon lattice:(a)Structure sketch;(b)the f i rst Brillouin zone.

在傅里葉變換下,選擇基矢量

Ψk=(c1k↑,c2k↑,c3k↑,c4k↑,c1k↓,c2k↓,c3k↓,c4k↓)T,實空間哈密頓量在動量空間可以寫成H =H(k)Ψk.H(k)表示為

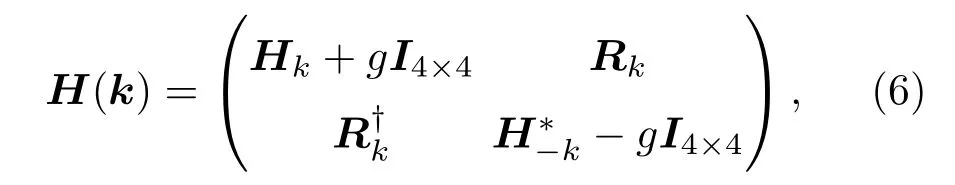
其中I4×4為4×4單位矩陣,Hk和Rk的具體形式如下

其中

2.2 自旋陳數和邊緣態

隨著對拓撲絕緣體的深入研究,可以根據不同的拓撲不變量對絕緣態進行分類.本文采用的拓撲不變量是陳數和自旋陳數.量子霍爾系統的拓撲不變量由陳數來表征,但對量子自旋霍爾系統,需要通過Z2拓撲數或者自旋陳數來刻畫.對于時間反演對稱的系統,自旋陳數和Z2指標是完全等價的.但是在時間反演對稱性被破壞后,不便再定義Z2拓撲數,而自旋陳數不依賴于任何對稱性,因此可以利用自旋陳數的概念,定義自旋陳數Cs=(C+?C?)/2,其中C±是自旋sz= ±1的能帶在第一布里淵區的Berry相位除以2π[8?10].自旋陳數被兩個譜隙所保護,一個是導帶和價帶之間的帶隙,另一個是自旋譜隙.自旋譜隙指的是自旋投影算符PσzP本征值的譜隙.只要滿足體能隙和自旋譜隙不為零,都可以定義自旋陳數.這里陳數C=C+?C?的計算可以采用已經發展成熟的數值方法[34,35].另一方面,研究系統的拓撲相變的另外一個有效的方法是計算邊緣態的能譜,拓撲絕緣體的邊緣態也直接跟體能帶的拓撲性質有關[36,37].為了研究邊緣態的性質,計算一個二維納米帶的能譜,其中y方向寬度為50個原胞,x方向為無限長,因此x方向的動量kx是好量子數.對于每一個動量值kx,通過精確對角化系統的哈密頓量H(kx),可以得到能譜E(kx)和對應的波函數邊緣態的自旋極化可以通過來描述.

3 數值結果與分析

3.1 時間反演對稱破缺的量子自旋霍爾效應

首先,考慮內稟自旋軌道耦合項λI對色散關系的影響.對角化哈密頓量H(k)可以得到squareoctagon晶格在第一布里淵區中沿著圖1(b)所示的高對稱點的色散關系,如圖2所示.系統中不存在Rashba自旋軌道耦合和交換場時,即λR=g=0,對應的四個能帶二重簡并.當λI=0時,最上面的三個能帶和最下面的三個能帶在Γ點和M點接觸(圖2(a)),能帶中不存在能隙,說明系統處于金屬態.當λI=0.1時,如圖2(b)所示,中間的兩個能帶在布里淵區中的所有點都是彼此分開的,但它們之間仍然不存在完整的能隙,即有一個負的能隙,因此它們的霍爾電導不是量子化的,系統整體表現為半金屬[38].相反,最上面和最下面的兩個能帶相互分開,產生完整的能隙,表明這時系統處于一種絕緣態.繼續增加Rashba自旋軌道耦合至λI=0.6時,如圖2(c)所示,系統的四個能帶獨立存在,彼此分開,并且有很大的能隙.接下來同時引入Rashba自旋軌道耦合和交換場,研究square-octagon晶格在自旋軌道耦合作用和交換場的影響下可能發生的拓撲相變.取參數λI=0.6,λR=0.05,g=0.1,如圖2(d)所示,自旋向上與自旋向下的能帶完全分開,系統在1/4,1/2和3/4填充時均處于絕緣態.

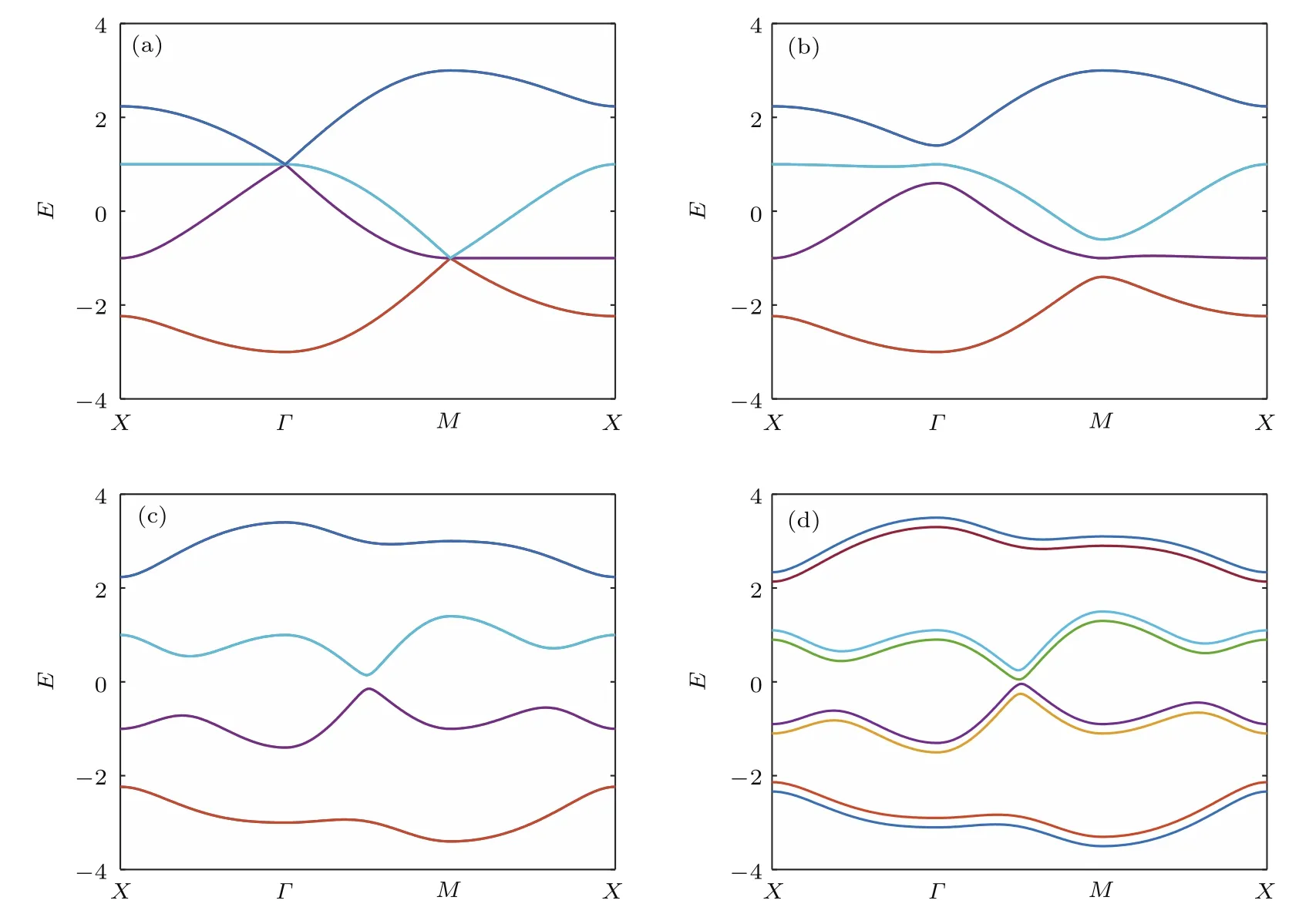
圖2 Square-octagon晶格在第一布里淵區內的色散關系 (a)λI=0;(b)λI=0.1;(c)λI=0.6;(d)λI=0.6,λR=0.05,g=0.1Fig.2 .Energy band of square-octagon lattice along the line between high symmetric points in the f i rst Brillouin zone:(a)λI=0;(b)λI=0.1;(c)λI=0.6;(d)λI=0.6,λR=0.05,g=0.1.

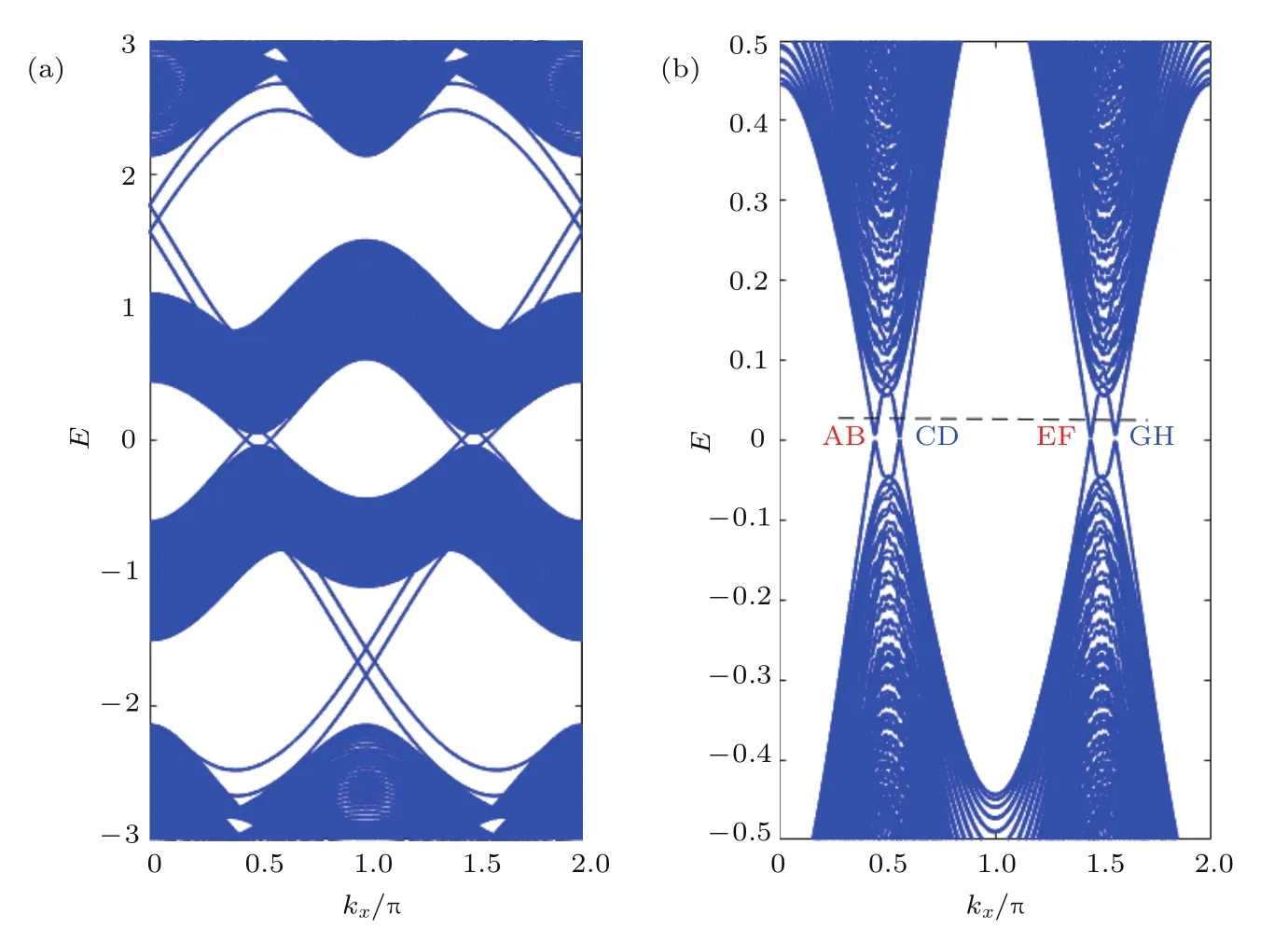
圖3 參數λI=0.6,λR=0.05,g=0.1情況下的square-octagon晶格 (a)邊緣態能譜;(b)1/2填充時的邊緣態Fig.3 .Square-octagon lattice for λI=0.6, λR=0.05,and g=0.1:(a)Energy spectrum;(b)edge states at 1/2 f i lling.

為確定系統是否為拓撲絕緣體,又計算了square-octagon晶格在參數λI=0.6,λR=0.05,g=0.1下的邊緣態模式,結果如圖3所示.系統在1/2填充時,對于給定的費米能級,很明顯有八個不同的邊緣態穿過能隙.在圖3(b)中,用A到H從左到右依次標記這八個邊緣態.為了清楚地了解邊緣態的模式,給出了邊緣態波函數|?|2在納米帶格點的概率分布和邊緣態的自旋極化,如圖4所示.發現邊緣態A,B,E和F局域在納米帶的一個邊界上,而C,D,G和H局域在另一個邊界上.以邊緣態A和邊緣態B為例,從能帶中A點和B點的斜率(即速度)很容易知道邊緣態A和邊緣態B是沿著相反的方向運動的.邊緣態的自旋極化標注在圖4(a)—圖4(h)中,盡管在考慮Rashba自旋軌道耦合作用λR以及交換場g之后,自旋在x和y方向的分量不再為零,但是z方向的自旋極化仍然占有很高的比率.我們發現邊緣態A自旋向下而邊緣態B自旋向上.以同樣的道理可以分析邊緣態E和邊緣態F的情況.最后總結出,在納米帶的一個邊界上,邊緣態A和B以及邊緣態E和F是兩對沿著相反方向運動并且自旋極化方向相反的螺旋邊緣態,即N↑=N↓=2,這與計算所得的自旋陳數Cs=2相對應,因此系統處于時間反演對稱破缺的量子自旋霍爾相[11].類似地,系統在1/4和3/4填充時,計算得到Cs=?1,這時在納米帶的每個邊界上存在著一對反向傳播的具有相反自旋極化的邊緣態,如圖3(a)所示,系統展現同樣的量子自旋霍爾效應.

圖4 邊緣態波函數|?|2在納米帶格點的的概率密度分布和邊緣態的自旋極化 (a)邊緣態A;(b)邊緣態B;(c)邊緣態C;(d)邊緣態D;(e)邊緣態E;(f)邊緣態F;(g)邊緣態G;(h)邊緣態HFig.4 .Probability density of the edge-state wavefunction|?|2of an ribbon and the spin polarizations of the edge states:(a)Edge state A;(b)edge state B;(c)edge state C;(d)edge state D;(e)edge state E;(f)edge state F;(g)edge state G;(h)edge state H.

3.2 自旋過濾的量子反常霍爾效應

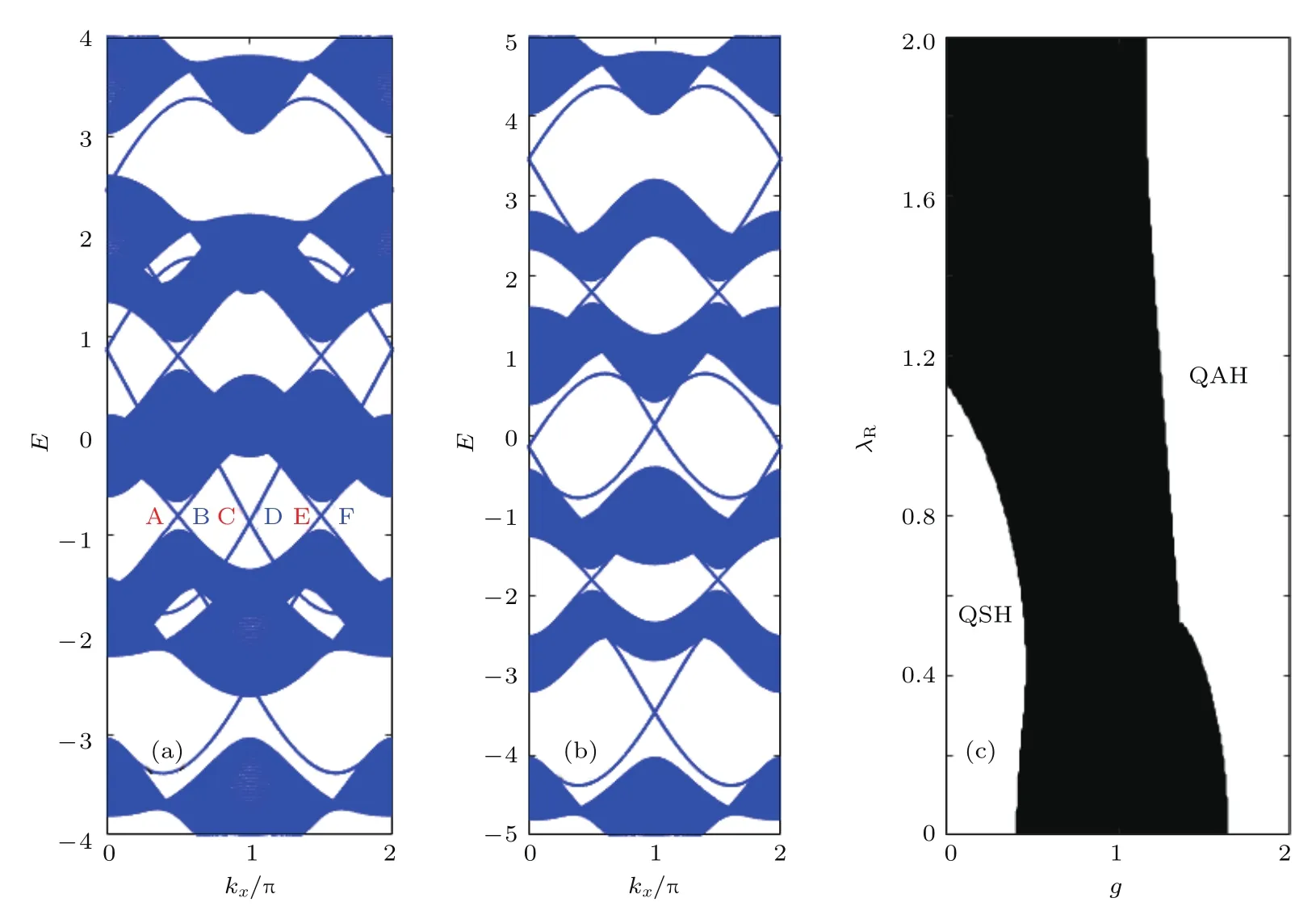
圖5 不同交換場下square-octagon晶格的邊緣態能譜以及1/4填充因子下的相圖 (a)λI=0.6,λR=0.05,g=0.8;(b)λI=0.6,λR=0.05,g=1.8;(c)λI=0.6,其中QSH表示量子自旋霍爾絕緣體,QAH表示量子反常霍爾絕緣體,黑色部分表示金屬Fig.5 .Edge state spectrum with dif f erent values of exchange f i eld and phase diagram of the square-octagon lattice at 1/4 f i lling:(a) λI=0.6,λR=0.05,g=0.8;(b) λI=0.6,λR=0.05,g=1.8;(c) λI=0.6.Here,QSH denotes the quantum spin Hall insulator,QAH denotes the quantum anomalous Hall insulator and the black color denotes a metal phase.

圖6 邊緣態波函數|?|2在納米帶格點的概率密度分布和邊緣態的自旋極化 (a)邊緣態A;(b)邊緣態B;(c)邊緣態C;(d)邊緣態D;(e)邊緣態E;(f)邊緣態FFig.6 .Probability density of the edge-state wavefunction|?|2of an ribbon and the spin polarizations of the edge states:(a)Edge state A;(b)edge state B;(c)edge state C;(d)edge state D;(e)edge state E;(f)edge state F.

增加交換場的大小,當g=0.8時,邊緣態能帶結構如圖5(a)所示.在3/8填充時,能隙中存在六個邊緣模式,分別標記為A,B,C,D,E和F,其波函數空間分布見圖6.很容易看出,邊緣模式A,C和E局域在納米帶的一個邊界上,沿著同一方向運動,而B,D和F局域在另一個邊界上,共同沿著另一相反的方向運動,此時納米帶邊界存在手征的邊緣態模式,因此系統處于量子反常霍爾態,計算得到陳數C=3.特別的是,邊緣態自旋向上的數目不等于自旋向下的數目,即N↑=1,N↓=2,從而貢獻自旋霍爾電導σSH=?e/4π,霍爾電導σH=3e2/h[39,40].類似地,在5/8填充時,N↑=2,N↓=1,對應C=?3.同時注意到,在1/8填充的情況下,納米帶的每個邊界上只有一條自旋向下的邊緣態,即N↑=0,N↓=1,計算得到C=?1,這意味著系統處于自旋過濾的量子反常霍爾態[39,40].相反,在7/8填充時,只有一條自旋向上的邊緣態存在于邊界上,即N↑=1,N↓=0,對應陳數C=1,如圖5(a)所示.繼續增大交換場至g=1.8,如圖5(b)所示,在1/2填充時,系統處于時間反演對稱破缺的量子自旋霍爾態,自旋陳數Cs=?1.系統在1/4填充時,納米帶的每個邊緣上有兩條自旋向下的邊緣態沿著同一方向傳播,即N↑=0,N↓=2,計算陳數C=2,系統處于自旋過濾的量子反常霍爾態.同樣地,系統在3/4填充時處于C=?2的自旋過濾的量子反常霍爾態.本文還通過直接計算各個參數下的陳數和自旋陳數,給出了square-octagon晶格處于1/4填充因子下的相圖.圖5(c)給出的相圖是Rashba自旋軌道耦合作用λR和交換場g的函數.從相圖中可以看到,square-octagon晶格支持量子自旋霍爾絕緣體和量子反常霍爾絕緣體的存在,并且Cs=?1的量子自旋霍爾相到C=2的量子反常霍爾相的轉變伴隨著體能隙的閉合.

將圖3(b)和圖5(b)中1/2填充時的量子自旋霍爾態相比較,可以看出,在邊緣上發生兩種情況:一種情況是邊緣態能隙打開,導致有能隙的邊緣態;另一種情況是在邊界上出現無能隙邊緣模式.投影自旋算符的矩陣元是〈?m(kx)|σz|?n(kx)〉,m和n遍歷所有被電子占據的態,通過對該矩陣對角化,可以得到自旋譜.對應于圖3(b)和圖5(b)中給定的參數,計算獲得的自旋譜如圖7(a)和圖7(b)所示.在圖7(a)中,當邊緣態能譜存在能隙時,自旋譜沒有出現能隙.對于無能隙的邊緣態,自旋譜只有兩個值±1,存在譜隙,如圖7(b)所示.因此量子自旋霍爾效應邊緣態能譜或自旋譜兩者之一必然表現出無譜隙的特征[41].

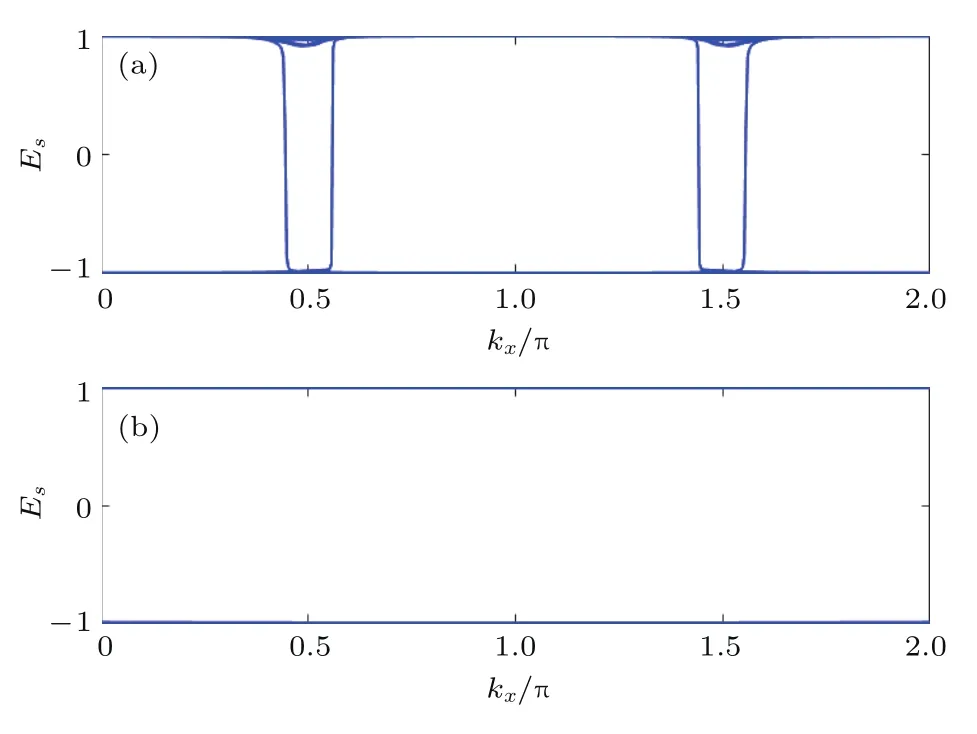
圖7 量子自旋霍爾邊緣態的自旋譜 (a)有能隙邊緣態;(b)無能隙邊緣態Fig.7 .Spin spectrum of quantum spin Hall edge state:(a)Gapped edge state;(b)gapless edge state.

4 結 論

基于陳數和自旋陳數,本文研究了squareoctagon晶格在自旋軌道耦合和交換場作用下的拓撲相變.在自旋軌道耦合和交換場的共同作用下,系統出現許多不同的拓撲相,包括自旋陳數Cs=?1,2的時間反演對稱破缺的量子自旋霍爾相和陳數C=±3,±2,±1的量子反常霍爾相.有趣的是,調節交換場的大小或者填充因子,系統發生了從螺旋量子自旋霍爾邊緣態到自旋過濾的手征量子反常霍爾邊緣態的相變.對于量子自旋霍爾系統,在鏡面對稱性和時間反演對稱性都被破壞的情況下,其邊界上的螺旋邊緣態可以是無能隙的,而對應的自旋譜存在著很大的譜隙.二維納米帶的邊緣態能譜和自旋譜與陳數和自旋陳數的拓撲表征相符合.

量子自旋霍爾效應在不受時間反演對稱性保護的情況下,仍然可以存在無能隙的螺旋邊緣態,這進一步拓寬了量子自旋霍爾效應的理論框架,為實現穩定的量子自旋霍爾效應提供了一個新方案.同時,square-octagon晶格具有一定的潛在應用價值,研究者已經在功能材料ZnO的(10ˉ10)中發現準square-octagon結構.另外,在一定的參數范圍內,square-octagon晶格中可以出現具有高平坦率的拓撲平坦能帶,為研究分數量子反常霍爾效應提供了一個新的晶格模型.就在最近,人們預言在square-octagon晶格中可以實現單軌道高溫s±超導態[29].此外,本工作的研究方法可以延伸推廣到其他典型的晶格系統[42,43],因此進一步探索square-octagon晶格中其他可能的拓撲非平庸態,例如分數量子反常霍爾態以及其他晶格中可能發生的奇異相變,將是很有意思的工作.而且,由于光晶格冷原子技術的發展,實驗上已經可以利用光晶格模擬Haldane模型[44],并且自旋軌道耦合和均勻磁場可以由激光和冷原子間相互作用來調控[45,46],為在實驗上觀測到這些拓撲相變和自旋操控提供了平臺.