Cr二維單層薄片中Jahn-Teller效應的第一性原理研究?

張薇1)2)? 陳凱彬1) 陳震東1)

1)(福建師范大學物理與能源學院,福建省量子調控與新能源材料重點實驗室,福州 350117)

2)(福建省半導體光電材料及其高效轉換器件協同創新中心,廈門 361005)

(2018年9月7日收到;2018年10月1日收到修改稿)

1 引 言

二維材料具有許多奇妙的物理效應和廣闊的應用前景,有望應用于納米器件、透明導電材料、電子邏輯器件、能量存儲材料[1]和自旋電子器件等.石墨烯是一種典型的二維材料,僅由C元素構成并且具有單原子層結構.2004年,單層石墨烯首次在實驗中被成功剝離[2],打破了先前的假設:平面石墨烯相對于富勒烯和納米管等曲面結構是不穩定的,不存在其自由狀態.2015年,單層WS2和WSe2在實驗中由熔鹽法成功制備[3].2018年,47種二維過渡金屬硫化物薄層再次于實驗中由熔鹽法輔助化學氣相沉積方法成功制備,包括單層NbSe2,MoTe2,MoS2,PtSe2,WTe2,ReSe2,VxWyMo1?x?yS2zSe2(1?z)合金等[4]. 隨著實驗技術的不斷進步和成熟,對處于自由狀態的二維單層原子晶體的探索已經引起了人們越來越多的關注.近年來,研究者對Cu低維體系[5],Nb二維原子薄片[6],W原子薄片[7]、鐵原子薄片[8]、鍺烯[9]、錫烯[10]、硅烯[11]以及二維蜂窩狀金[12]等二維體系進行了理論研究.對二維Cr薄膜的理論計算可以幫助探究其處于低維結構時的晶格結構和電子性質.采用基于密度泛函理論的第一性原理計算,本文首先計算了一個原子層厚度的Cr薄膜分別處于長方、正方、六角、斜方和中心長方晶格下的結構穩定性和能帶結構性質.然后,進一步計算了單層Cr薄膜的電子態密度和總電荷密度等性質.最后,討論了Jahn-Teller效應對d軌道電子占據情況的影響,揭示了其穩定結構形成的機理.

2 理論計算方法

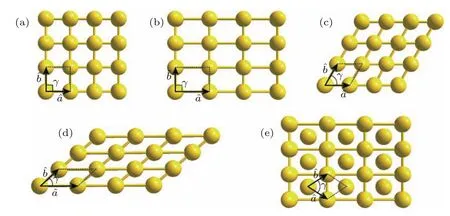
圖1 二維Cr原子薄片的不同結構和原胞 (a)正方晶格(a=b,γ=90?);(b)長方晶格(a=b,γ=90?);(c)六角晶格(a=b,γ =60?);(d)斜方晶格 (a≠b,γ≠90?);(e)中心長方晶格(a=b,γ≠60?,90?)Fig.1 .Crystal structures and primitive cells for various 2D chromium atomic sheets:(a)Square lattice(a=b,γ =90?);(b)rectangular lattice(a≠b,γ =90?);(c)hexagonal lattice(a=b,γ =60?);(d)oblique lattice(a≠b,γ≠90?);(e)centered rectangular lattice(a=b,γ≠60?,90?).

采用基于密度泛函理論的第一性原理計算軟件包VASP[13,14](Vienna ab initio simulation package).該軟件包采用平面波展開,映射綴加波勢(projector augmented-wave potentials,PAW)[15,16]以及廣義梯度近似(generalized gradient approximation,GGA)[17].我們計算了Cr的一系列二維布拉赫格子(正方晶格、長方晶格、六角晶格、斜方晶格和中心長方晶格),晶格結構如圖1所示.真空層大小設置為15 ?,平面波截斷能量設置為400 eV,布里淵區積分采用Monkhorst-Pack方法[18],k點網格選取為15×15×1,電子占據數fnk采用Bl?ch修正的四面體方法來處理[19].

3 結果與討論

3.1 結構性質與Jahn-Teller效應

首先,計算得到Cr二維原子薄片所有可能結構的晶格常數和結合能,進而根據結合能來判斷各結構是否可以穩定存在.計算得到體心立方Cr晶格常數為2.83 ?,與常溫常壓下Cr的晶格常數2.88 ?[20]較符合.然后,研究Cr的所有二維晶體結構(包括正方、長方、六角、斜方和中心長方晶格,如圖1所示),結構優化后所得的晶格常數和結合能列在表1中.

從表1可以看到,二維結構的配位數均小于體結構的配位數.二維Cr的中心長方結構的鍵角比六角結構的大13.6?,鍵長比六角的鍵長小0.12 ?,結合能比六角的大0.09 eV/atom.Cr的斜方結構的鍵角比六角結構的小11?,平均鍵長比六角的長0.16 ?,結合能與中心長方結構的結合能相等,但比六角結構的結合能大0.09 eV/atom.另外,正方結構的結合能比中心長方和斜方晶格結構(結合能最高)的小0.06 eV/atom,比六角結構大0.03 eV/atom.這說明Cr的二維結構中,斜方結構和中心長方結構比六角結構、正方結構穩定.

表1 Cr原子薄片在不同二維結構下的平衡晶格常數和結合能Table 1 .Lattice constants and cohesive energies Ebfor various 2D chromium atomic sheets.

圖2 Cr二維體系總能量相對于晶格常數/鍵角的變化Fig.2 .Total energy of 2D Cr system changes with lattice constants and bond angle.

接下來,具體計算體系能量隨鍵角和晶格常數的變化,結果以三維曲面圖展現,如圖2所示.x軸代表晶格常數a(?),y軸代表基矢a和b的夾角γ(?),z軸表示體系總能量(用顏色梯度標識能量,顏色越深說明體系的總能量越低).由圖2可以看出,Cr的二維正方結構在能量曲面上對應的位置為鞍點,故Cr的正方晶格結構是不穩定結構;而中心長方結構對應的是曲面的谷,因此中心長方結構是穩定的.

為了更直觀地看出體系總能量隨結構參數的變化規律,進一步繪出圖2的二維投影圖,即不同結構參數的能量等高線,如圖3所示.在圖3中可以看到兩個顏色最深的橢圓面,代表總能量最低的體系,分別為二維中心長方結構和二維斜方結構,再次證明這兩種結構是二維穩定結構.

由于Jahn-Teller效應,在Cr的不同二維結構中,結構對稱性較低的中心長方結構和斜方結構的結合能大于對稱性較高的六角結構的結合能.可以這樣理解,二維Cr的六角結構的鍵角γ沿著大于或小于60?的方向畸變,使結構的體系對稱性降低,結構畸變為穩定的中心長方結構或者斜方晶格結構.簡并的能級被破壞,結構產生畸變,使體系能量變得更低.

所有二維結構的Cr原子薄片的結合能都比體心立方Cr的低,這與晶格結構中原子成鍵的難易程度有關.從表1中的鍵長來看,Cr的所有二維結構的鍵長都小于體結構體心立方的鍵長,說明二維薄片原子間的成鍵比體結構的更強.接下來分析不同結構Cr的配位數情況.一般地,金屬的結合能隨配位數增大而增大.Cr的體結構的配位數最高為8,結合能也最高(5.20 eV/atom).Cr的二維正方結構配位數最低,結合能也較低,為3.08 eV/atom.Cr二維斜方和中心長方晶格結構的結合能都為3.14 eV/atom,大于正方結構的結合能,小于體結構的結合能.這是因為正方結構的配位數為4,斜方和中心長方結構的配位數為6,而體材料的配位數為8.

圖3 Cr二維體系能量的等高線圖Fig.3 .Energy contour map of Cr 2D system.

3.2 電子結構性質分析

下面通過電子結構進一步研究Cr二維體系中的Jahn-Teller效應.圖4為Cr不同結構的能帶圖,可以看出各結構均有能帶穿過費米能級,反映了體結構及各種二維結構Cr的金屬性.二維晶格的Cr體系有比較多的能帶穿過費米能級,而體心立方晶格穿過費米能級的能帶數則較少.以圖4(c)的二維六角晶格Cr為例,它的能帶在費米能級附近被部分填充,部分填充的能帶具有簡并性或近似簡并性.這種簡并能級會由于自發破缺,使結構向對稱性低的結構形變,從而使體系變為能量更加穩定的狀態.因此,對稱性低的中心長方和斜方結構比六角結構更加穩定.和體結構對比,二維結構的能帶變窄,這一方面是由于維度的降低導致電子運動受到限制,使得價電子的運動受到強的約束;另一方面是由于二維結構配位數降低,外場對電子的束縛減弱,使得電子能量上升,能帶向費米面發生移位,從而使費米面附近的電子態密度有所增加.

圖4 Cr不同結構的能帶圖 (a)體結構;(b)二維正方晶格;(c)二維六角晶格;(d)二維斜方晶格;(e)二維中心長方晶格Fig.4 .Energy bands for dif f erent Cr structures:(a)Bulk lattice;(b)2D square lattice;(c)2D hexagonal lattice;(d)2D oblique lattice;(e)2D centered rectangular lattice.

圖5 Cr不同結構的總電子態密度圖 (a)體結構;(b)二維正方晶格;(c)二維六角晶格;(d)二維斜方晶格;(e)二維中心長方晶格Fig.5 .Total electronic density of states for various Cr structures:(a)Bulk lattice;(b)2D square lattice;(c)2D hexagonal lattice;(d)2D oblique lattice;(e)2D centered rectangular lattice.

接下來計算各種不同結構的Cr體系的電子態密度.在費米能級處,Cr的體結構(體心立方)及各種二維晶格結構的總電子態密度均不為零,反映了這幾種結構都是金屬性的,這與能帶計算結果一致(如圖5所示).相較于體心立方Cr體系中電子態密度的分布,二維各種結構在費米面附近電子態占據均變多.對費米能級以下的電子態密度積分可以得到二維斜方Cr和二維中心長方Cr費米能級下填充的電子數比二維六角Cr多,導致整個體系的總能變低.這正是由于Jahn-Teller效應破缺了六角結構的能級簡并性,體系結構轉變為兩種對稱性較低的穩定結構.

3.3 電荷密度及軌道電子占據情況分析

圖6是Cr體心立方(100)和(110)晶面、各種二維晶格結構的電荷密度等高線圖.從圖6可見,二維結構的電荷密度圖與體結構相似,并且二維結構的成鍵沒有明顯的方向性.體結構電荷密度等高線呈球形對稱,二維正方結構的電荷密度等高線略微偏離球形對稱,二維斜方和二維中心長方晶格的電荷密度等高線與球形偏離較大,產生一定畸變.

最后計算Cr二維結構(六角、斜方和中心長方)各個軌道在費米面下的電子占據數目,結果如表2所列.由表2可見,二維六角Cr的dxy和dx2?y2軌道上各占據約1個電子,軌道是簡并的,能量較低;dyz,dz2和dxz軌道上各占據電子約0.7個,軌道也是簡并的,能量較高.五條d軌道共占據電子數4.191.當二維六角Cr畸變為二維中心長方晶格時,五條d軌道的電子占據數分別為0.997,0.418,1.34,0.740,0.828,總數為4.323.因此,Jahn-Teller效應導致系統對稱性降低,解除了dxy和dx2?y2的能級簡并,也解除了dyz,dz2和dxz的能級簡并,導致總電子占據數增多,體系能量降低.當體系畸變為二維斜方結構時,五條d軌道的電子占據數分別為1.08,0.928,0.734,0.828,0.978,總數為4.557.同樣地,Jahn-Teller效應解除了dxy和dx2?y2的能級簡并,也解除了dyz,dz2和dxz的能級簡并,總電子占據數亦增多,體系能量降低.所以,Jahn-Teller效應使能級簡并解除,導致Cr畸變為穩定的二維中心長方和二維斜方晶格結構.

圖6 Cr不同結構的電荷密度等高線二維投影圖 (a)體心立方(100)晶面;(b)體心立方(110)晶面;(c)二維正方晶格;(d)二維六角晶格;(e)二維中心長方晶格;(f)二維斜方晶格Fig.6 .2D charge density contour of various Cr structures:(a)bcc lattice(100);(b)bcc lattice(110);(c)2D square lattice;(d)2D hexagonal lattice;(e)2D centered rectangular lattice;(f)2D oblique lattice.

表2 Cr的二維六角、斜方和中心長方晶格各個軌道電子占據數目Table 2 .Electron occupation numbers of orbitals in 2D hexagonal,rhombic and central rectangular Cr.

圖7 Cr二維中心長方、六角和斜方的d軌道能級分裂Fig.7 .D-orbital energy splitting in 2D central rectangular,hexagonal and oblique structures of Cr.

為了更直觀地理解Jahn-Teller效應的影響,繪出六角Cr畸變為二維中心長方和二維斜方晶格時d軌道能級分裂情況的示意圖,如圖7所示.

如上所述,二維Cr原子晶體兩種穩定的結構都是二維六角結構畸變的結果,二維六角結構的鍵角γ增大形變成二維中心長方結構,鍵角γ減小形變成二維斜方結構.由此可見,Jahn-Teller效應對二維原子薄片的結構穩定性起到了決定性作用.實驗制備二維結構可以用外延法將單層膜生長在基底材料上來穩定其結構.由于二維斜方和中心長方結構是由六角結構畸變而來的,所以這兩種結構及六角晶格的基底材料可選為Ni[21],Cu(111)[22]等.

4 結 論

采用基于密度泛函理論的第一性原理,本文計算了Cr原子薄片所有二維結構的電子結構性質,分析了它們的成鍵特點,能帶結構以及電荷密度分布、d軌道占據情況等特征.計算結果表明Jahn-Teller效應對二維結構的穩定性和電子結構具有顯著影響.由于Jahn-Teller效應,Cr的二維正方晶格和二維六角晶格是不穩定的,二維中心長方晶格和二維斜方晶格是穩定的.這是因為Jahn-Teller效應使體系對稱性降低,解除了晶格的簡并,結構畸變成對稱性較低的二維中心長方晶格和二維斜方晶格結構.以上對Cr單層薄片的研究有助于二維體系的材料設計及實驗合成,亦為納米器件的研發和制備指明了方向.