二維圓柱形亞波長結構集成芯片的設計方法

王加科，張雷夢婷 ，鄭陽，何峰，邱偉

（1.長春理工大學 光電工程學院，長春 130022；2.長春理工大學 光電測控與光信息傳輸技術教育部重點實驗室，長春 130022；3.上海航天控制技術研究所，上海 201109）

衍射透鏡與諧衍射透鏡設計和制作方法已經很成熟，通過臺階的高低實現相位差，從而達到調制波前相位的目的[1]。衍射透鏡可以用傳統套刻法和激光直寫的方法制作而成，而多次刻蝕導致多臺階式衍射元件加工精度大大降低。本文采用的二維圓柱形亞波長結構只需要一次刻蝕即可，適合高精度批量生產。

亞波長結構相當于多層折射率漸變的薄膜，可以降低菲涅爾反射[2]，通過改變它的形狀、周期、占空比、刻蝕高度等參數，得到不同的等效折射率，用于增加光學元件表面透過率。亞波長結構的制造工藝有很多[3，4]已經成功應用于太陽能電池表面等。由于亞波長結構形狀的不同，可以將其應用于抗反射薄膜[5]、濾波片[6]、閃耀光柵[7]等。通過嚴格耦合波理論計算可知，當亞波長結構周期足夠小時，透射光不存在高級次衍射[8]，這使得亞波長結構的應用得到拓展。由于全介質亞波長結構對光相位的調制能力，Philippe Lalanne等人提出高效率惠更斯表面[9]；由于全介質亞波長結構的會聚能力，Fanglu Lu和D.Fattal等人提出一維光柵透鏡[10，11]。Paul R.West等人運用等效介質折射率理論，進行了圓柱形亞波長結構衍射透鏡設計，制作了單個衍射透鏡，實現了紅外波段的高斯光束會聚[12]。但該結構口徑有120μm，不利于集成化設計。

嚴格耦合波理論（Rigorouscoupled-wave analysis，RCWA）和等效介質折射率理論（Effective medium theory，EMT）已經證明了亞波長結構等效折射率隨占空比增大而增大[13，14]。本文利用時域有限差分方法（Finite difference time domain，FDTD）計算等效折射率，并列出不同半徑亞波長結構的等效介質，通過計算結果設計一個口徑僅有4μm，厚度僅為1μm的衍射透鏡，以實現在折射率為1.4的介質中對400nm～800nm波段的會聚。該方法可用于設計滿足光學系統集成化要求的衍射透鏡，有利于集成芯片批量生產。

1 理論基礎

1.1 計算亞波長結構周期

光透過光柵后，會產生高級次衍射光，根據光柵常數與衍射級次的關系，能設計出各種衍射元件。一維亞波長光柵使偏振態與光柵方向平行的光透過率大，與光柵方向垂直的偏振光透過率低，導致出射光偏振態與入射光不一致，因此本文主要研究圓柱形二維光柵。在FDTD軟件中創建了圓柱型二維光柵模型，其折射率為1.4，周期為1μm，半徑為400nm，設置X-Z平面為結構截面圖，光源為X方向偏振的線偏振平面波，位于結構上方Z=0.8μm處，垂直射入結構，對其進行仿真計算，結果如圖1所示。

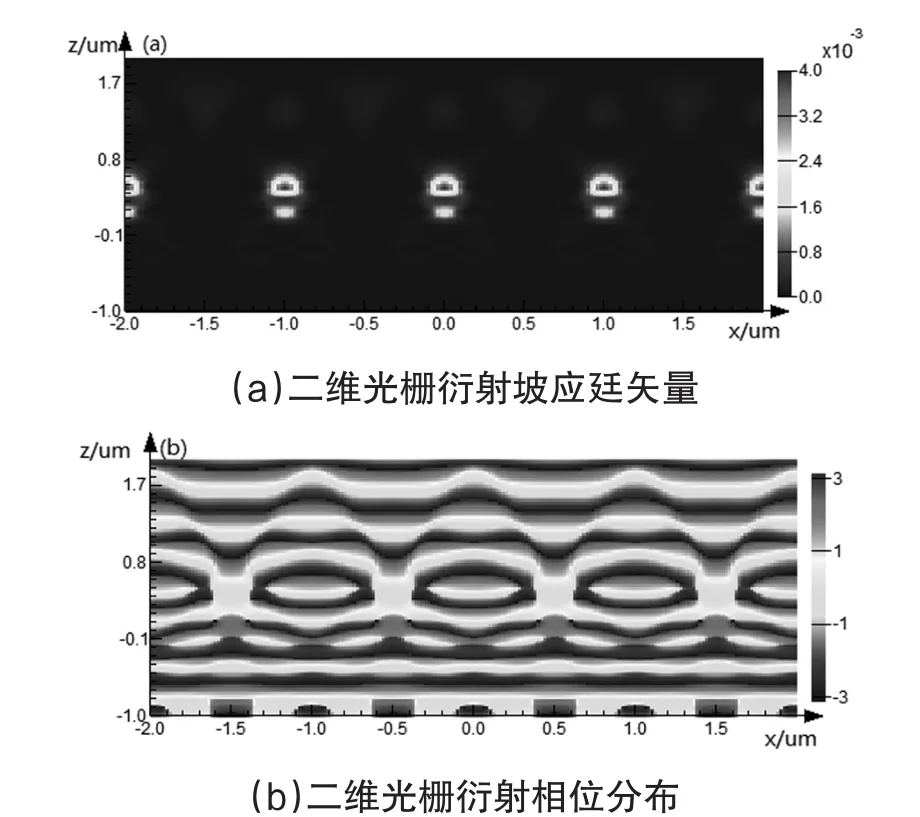
圖1 二維光柵衍射效果

圖1（a）所示，深色區域為光強較大區域，淺色為光強較弱的區域，證明了該結構使出射光能量分布發生改變，不再是平面波。圖1（b）為相位分布圖，深色區域與淺色區域交替表示相位值為-π～π，波前相位圖彎曲的地方光強大。圖1證明了該二維光柵使光場能量重新分布，不再是均勻分布，具有多級次衍射光。這將導致所設計的衍射透鏡具有多焦點，不利于成像和探測。

為了使光透過光柵后只存在零級衍射，高級次衍射光變成倏逝波，則需要光柵尺寸足夠小。當光柵特征尺寸和入射光波長相當時，光場計算不能再用標量衍射理論，其矢量特性不能忽視，因此采用嚴格耦合波方法和時域有限差分方法計算光場分布較為準確。嚴格耦合波理論在衍射結構的分析和設計中得到了廣泛的應用，是一種相對直接的、非迭代的、確定性的分析方法，根據嚴格耦合波理論[7]得出：

當入射光波為正入射（θ≠0°）時，反射波只存在零級衍射，須滿足：

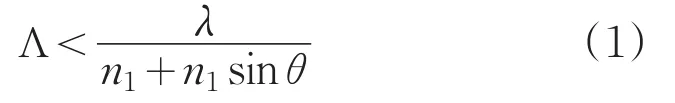
透射波只存在零級衍射須滿足：

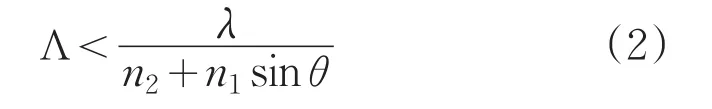
其中，θ為入射角度，其中λ為入射光波波長，n1為空氣折射率，n2為基底折射率。為了使任意角度入射光波透過圓柱形亞波長結構后不存在高階衍射，取θ=90°，由公式（2）可知其周期應該滿足：

取基底折射率為1.4時，針對入射光波段為400nm～800nm，其亞波長結構周期必須滿足0＜Λ＜166nm。取周期為100nm時，即可滿足消高級次衍射光的條件。如圖1所示為周期100nm，半徑為40nm的圓柱形亞波長結構。

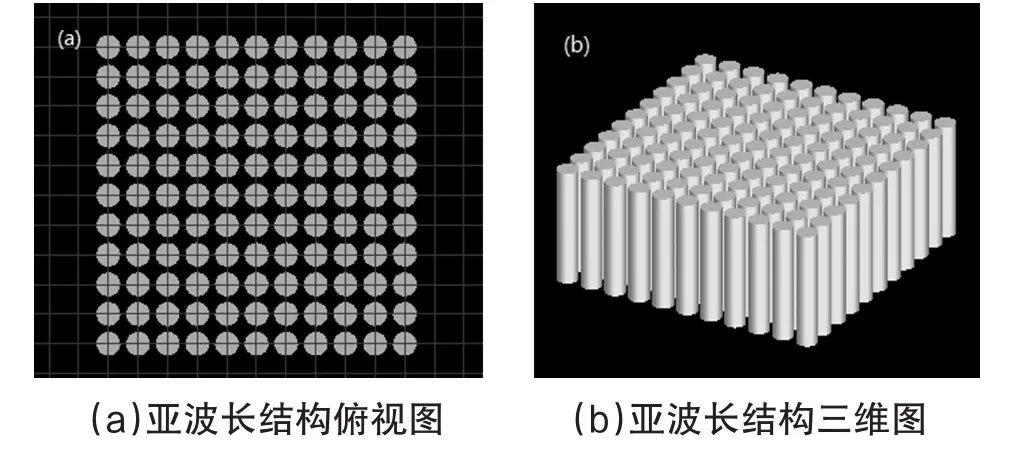
圖2 圓柱形亞波長結構

當光柵結構尺寸過大時，光透過光柵結構會產生高級次光，通過嚴格耦合波分析，得出消除高級次光需要滿足的周期條件，并選擇了結構周期為100nm的圓柱形二維亞波長結構，能滿足消透射光高級次的要求。

1.2 計算亞波長結構等效折射率值

時域有限差分方法是Kane S.Yee提出的方法，將解域離散化成空間網格，并把帶時間變量的麥克斯韋旋度方程轉化為差分格式，并采用空間、時間差半個步長的離散網格形式，用前一個時刻的電場值和磁場值，得到現在時刻的電場值和磁場值，并在每一時刻都計算空間域的電磁場。每個磁場分量由四個電場分量環繞，每個電場分量由四個磁場分量環繞。取樣方式符合法拉第電磁感應定律和安培環路定律。電場和磁場在時間上交替抽樣，抽樣時間彼此相差半個時間步。

為計算周期100nm，半徑不同的亞波長結構的等效折射率值，采用軟件FDTD-solutions對不同半徑的亞波長結構進行仿真模擬，從相位延遲量計算出亞波長結構的等效折射率。建模結構為半徑40nm，周期100nm的亞波長結構，將入射光設置為X軸向的線偏振平面光，為避免產生邊緣效應使平面波波前變形：與光軸平行的方向采用周期性邊界條件，與光軸垂直方向采用完美吸收匹配層。沿Z軸方向上，0～2μm處為亞波長結構區域，2～4μm處為空氣。結果如圖3所示，圖3a、3b、3c、3d分別表示E矢量分布、H矢量分布和相位分布及沿光軸方向的相位曲線圖。圖3a、3b表示，有亞波長結構的區域，磁場和電場均被調制，但離開亞波長表面后，光波電磁場均勻，表明出射光依舊為平面波。圖3c、3d表示，有亞波長結構的區域相比于無亞波長結構的區域產生相位延遲，根據相位延遲量可以計算該亞波長結構對應的等效折射率，計算原理為：

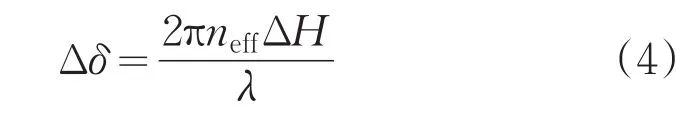
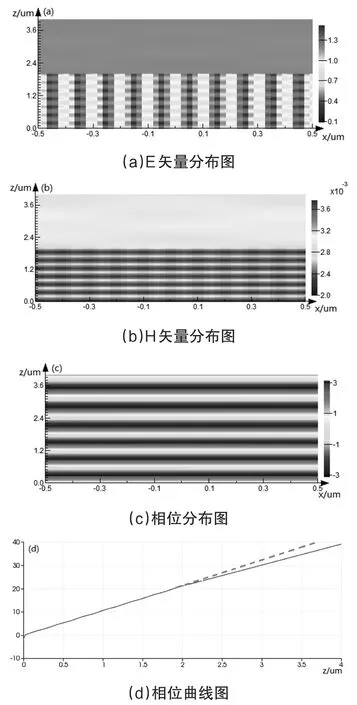
圖3 圓柱形亞波長結構的波前調制能力

重復上述步驟，分別計算不同半徑亞波長結構的相位隨厚度H的變化規律，并利用公式（2）計算出等效折射率值，其對應關系如表1所示。

表1 半徑與等效折射率值的關系

由表1可知，亞波長結構半徑越大，其等效介質折射率越大，但半徑與等效折射率值不成正比關系。

為了驗證計算結果，并證明二維圓柱形亞波長結構確實能實現0～2π的連續相位調制，將建模改為：不同半徑的亞波長結構依次從左往右排列開，得到一個調制波前的相位板，該相位板從左往右等效折射率依次增大。將入射光設置為沿X方向線偏振平面光，入射光波長為700nm，與光軸平行的方向采用周期性邊界條件，與光軸垂直方向上采用完美吸收匹配層，探測器沿光軸方向放置，與光軸平行。

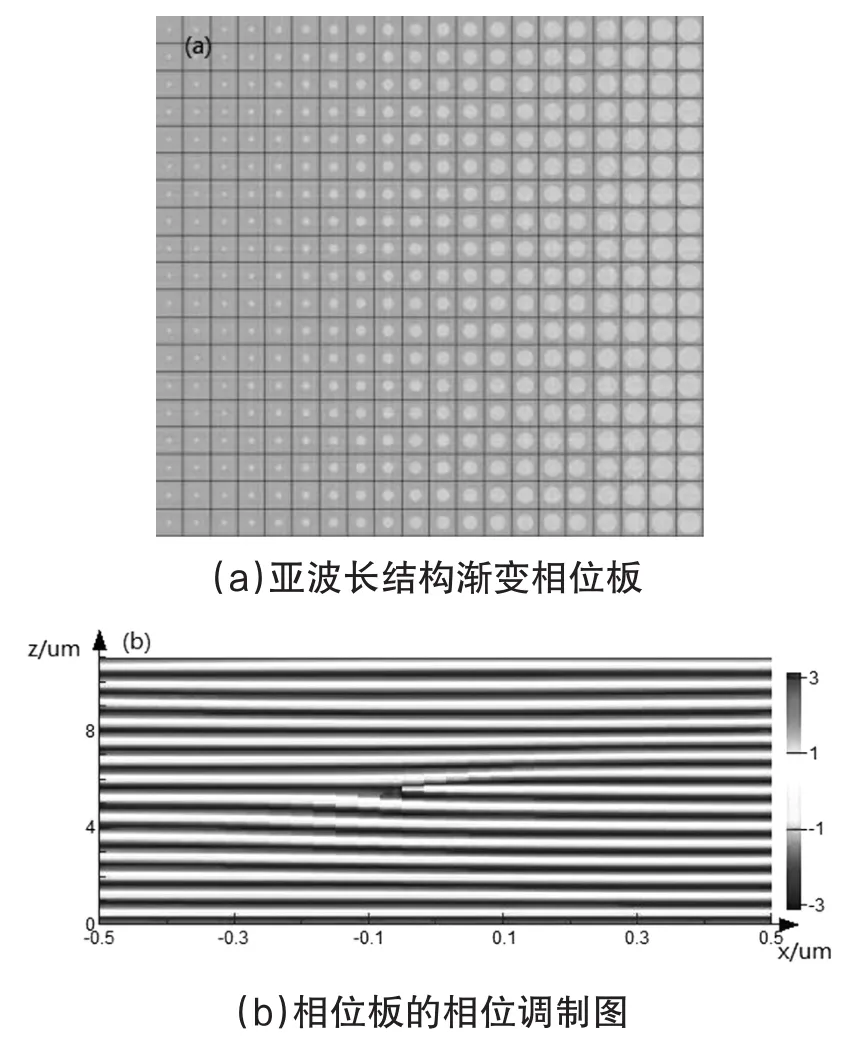
圖4 亞波長結構連續調制相位能力

計算結果如圖4所示。圖4（a）為半徑依次增大的亞波長結構，圖4（b）為光通過相位板后的相位分布，深色與淺色線條表示相位由-π～π變化，左右兩邊正好相差一個2π。亞波長結構半徑從左往右依次增大，相當于折射率從左往右逐漸增大的相位板，證明了二維圓柱形光柵確實可以實現連續相位調制。使得亞波長結構可以制作成渦旋光相位板，平面衍射透鏡等。

2 設計與仿真

衍射會聚透鏡需滿足：透鏡中心區域產生的相位延遲大于透鏡邊緣區域產生的相位延遲，由透鏡中心向外相位延遲量逐漸降低。

2.1 全介質圓柱形亞波長結構透鏡的設計

與衍射透鏡和諧衍射透鏡不同之處在于：其高度各處相等，只等效折射率值不同。因此，衍射會聚透鏡需將半徑大的亞波長結構排列在光軸附近，沿光軸中心向外徑向依次減小，原理如圖5所示，透鏡中心等效折射率大，邊緣等效折射率小。

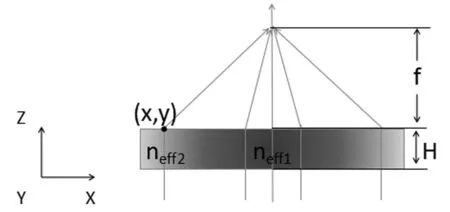
圖5 衍射會聚透鏡原理圖

產生相位差與焦距的關系為：

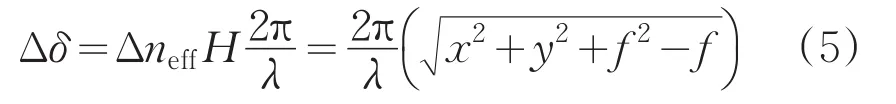
其中，Δneff=neff1-neff2，(x,y)表示出射光位置坐標。

2.2 圓柱形亞波長結構透鏡光強會聚仿真

對所設計的圓柱形亞波長結構會聚透鏡進行仿真，采用400nm～800nm線偏振平面光入射到衍射透鏡上，介質折射率為1.4，全介質圓柱形亞波長結構透鏡厚度為1μm，口徑為4μm。采用所有邊界條件為完美吸收匹配層，得到光波會聚圖樣。圖6（a）為各波長光垂直入射，透過圓柱形亞波長結構透鏡后的坡應廷矢量分布。從左到右分別為800nm、640nm、533nm、457nm、400nm光入射，透過全介質圓柱形亞波長結構透鏡后的會聚圖樣。深色區域表示光強最大，隨著波長減小，焦距增大，由左向右圖案表明，波長越小焦距越大。

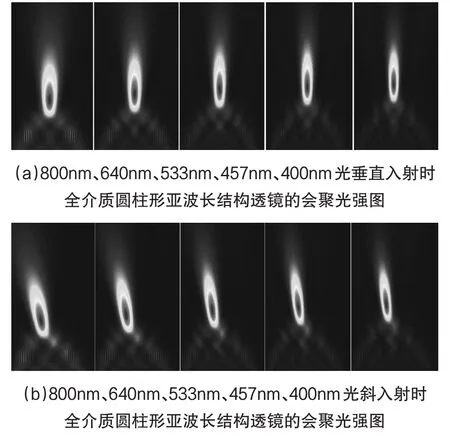
圖6 會聚光強圖

圖樣表明亞波長結構可以在厚度為1μm的情況下，實現高數值孔徑的會聚。同時能夠觀察到圓柱形亞波長結構透鏡有與傳統透鏡相反的色差，800nm光焦距短，400nm光焦距較長。與傳統透鏡相結合時，可以有效消除色差。圖6（a）為各波長光5°入射，800nm、640nm、533nm、457nm、400nm光透過亞波長結構透鏡后的圖樣。

衍射會聚透鏡用于集成光路中是很有意義的，能很大程度提高光學系統集成度，將該會聚透鏡排列形成陣列，得到與光軸方向垂直的多光束會聚，相當于微透鏡陣列，該系統的厚度僅為1μm，并且該衍射會聚透鏡適用于所有光學材料，這增大了該衍射會聚透鏡的適用范圍。如圖6所示為多光束會聚圖樣，入射光波長為800nm，與光軸平行方向為周期性邊界條件，與光軸垂直方向為完美吸收匹配層。

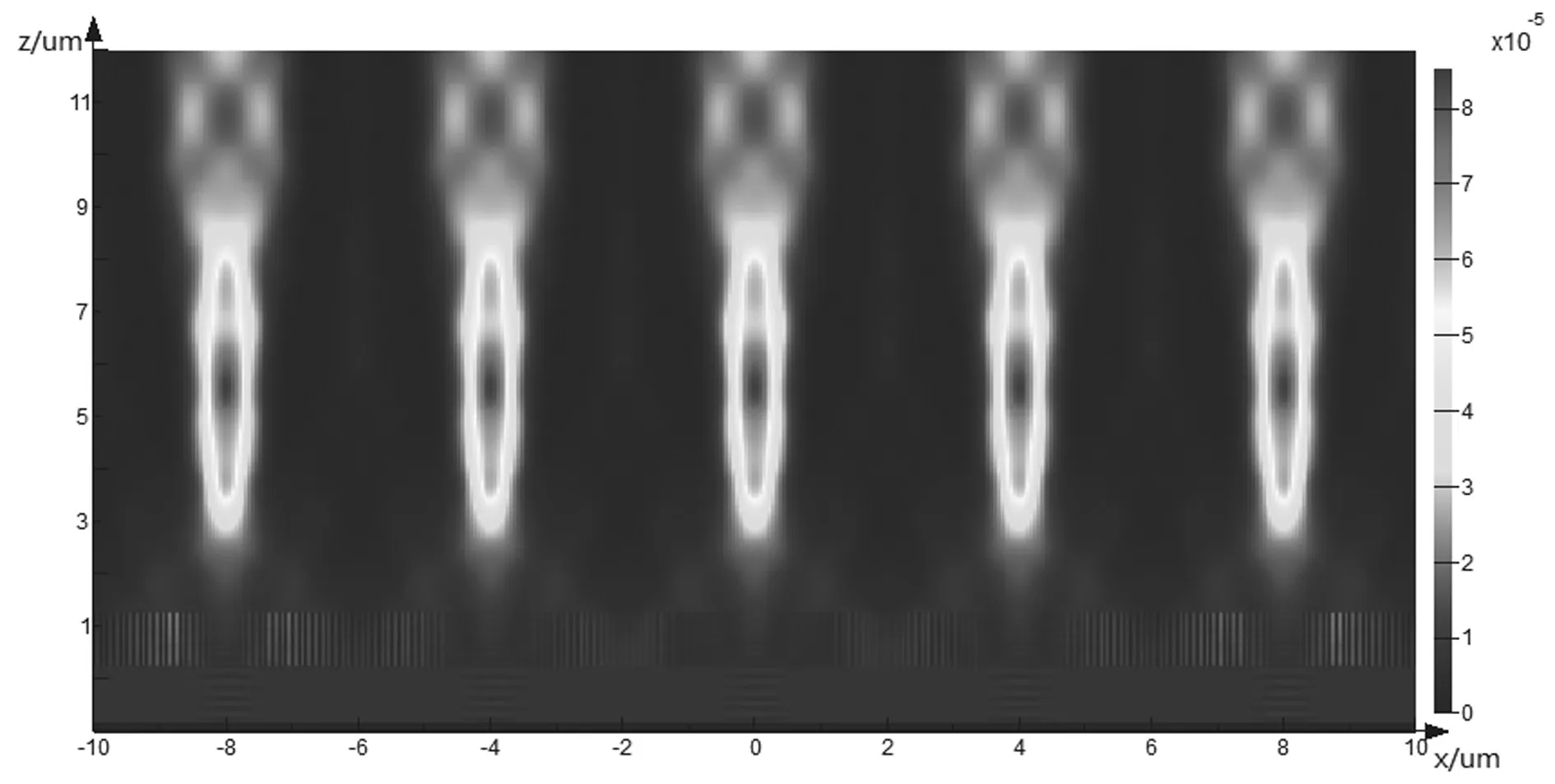
圖7 集成衍射型微透鏡陣列會聚光強圖

圖7所示，陣列排布的衍射會聚透鏡結構實現了數值孔徑約為0.72的多光束會聚，該系統非常緊湊。微透鏡陣列在均勻光系統、光場成像、波前傳感器等領域有著廣泛的應用。當光透過物體或物體反射時，波前相位發生變化，用集成微透鏡陣列作為探測器，將探測器中小衍射透鏡的會聚光斑位置讀取出來，并反向計算波前信息，由波前信息又可以算出物體的面型特征。由于該芯片各個結構高度相同，因此只需要一次刻蝕即可，極大的提高了加工精度。

3 結論

本文提供了一種設計亞波長結構芯片的方法，通過時域有限差分方法計算出不同形狀的亞波長結構的等效折射率值，并依據相位分布優化設計亞波長結構器件。亞波長結構不受基底材料的限制，光學材料都可以用于制作亞波長器件，因此，無論是單獨使用亞波長結構制作的會聚透鏡（陣列集成芯片），或是與傳統光學系統相結合都是很有意義的。同時該結構只需進行一次刻蝕加工，使得加工精度得到很大提高。