在運籌學教學中融入數學建模思想的應用＊

季海波

?

在運籌學教學中融入數學建模思想的應用＊

季海波

（宿遷學院 文理學院，江蘇 宿遷 223800）

通過一個“選課策略”的案例，把數學建模的思想引入到運籌學課程教學過程中，啟發學生如何利用0-1整數規劃進行建模，并通過Lingo軟件進行編程求解，既培養學生利用理論知識解決實際問題的能力，又提高學生的計算機應用能力。

運籌學；數學建模；Lingo軟件；應用能力

1 運籌學概述

運籌學是一門以人機系統的組織、管理為對象，應用數學和計算機等工具來研究各類有限資源的合理規劃使用，并提供優化決策方案的學科，是一門理論和實踐應用并重的綜合性學科[1]。運籌學應用范圍廣泛，從軍事、政治到管理、經濟及工程技術等許多領域都能應用到運籌學的思想和方法。運籌學和數學建模是很多高校數學與應用數學和信息與計算科學專業的核心課程。構成運籌學的理論大致分為分析理論、決策理論和隨機服務理論，而運籌學主要包括的內容有線性規劃、整數規劃、目標規劃、動態規劃、圖與網絡分析、存儲論、排隊論、決策論、博弈論等。而將數學建模的思想融入到許多數學核心課程的相關研究已經有了不少的研究成果[2-4]。而對運籌學的這門課程在不同專業的教學改革研究也有了不少比較好的結果[5-8]，運籌學這門課程本身絕大部分理論內容都是通過解決實際問題抽象出來的，因此在本課程的講授過程中融入建模思想是非常合適的，而且在建模的過程中，除了介紹對應的理論方法外，還可以根據模型利用Lingo軟件編程進行求解，訓練學生的計算機應用能力，這樣也就更加符合信科專業的培養目標——培養“應用型”人才。

2 建模思想在運籌學教學中的實際應用

本文主要通過選取一個與學生切身相關的案例“選課策略”來研究如何在運籌學教學中融入建模思想，在教學過程中既能夠鍛煉學生解決實際問題的能力，又能了解所需要學習的理論內容，求解過程可以融入計算機編程，鍛煉學生的動手能力。以信息與計算科學專業為例，表1給出了該專業其中9門課程的具體情況。

選課要求學生至少要選兩門數學課、三門運籌課和兩門計算機課。

問題1：為了選擇的課程門數最少，應該如何選擇課程？ 對于該“選課策略”問題，首先需要引導學生根據題目要求該如何假設我們的決策變量。假設決策變量的原則是，除了假設出對應的變量后，還能夠較容易地利用設出來的決策變量建立出模型的目標和相應約束條件。

表1 信息與計算科學專業課程情況

課號課程名稱學分所屬類別先修課程 1數學分析5數學 2高等代數4數學 3最優化方法4數學、運籌數學分析、高等代數 4數據結構3數學、計算機計算機編程 5應用統計4數學、運籌數學分析、高等代數 6計算機模擬3計算機、運籌計算機編程 7計算機編程2計算機 8預測理論2運籌應用統計 9數學實驗3運籌、計算機數學分析、高等代數

由于每個學生與每門課程之間只有選與不選兩種情況，因此可以考慮整數規劃中的0-1規劃，假設決策變量為：

下一步根據問題1建立模型的目標函數，為：

最后一步尋找約束條件，其中第一塊約束條件是選擇每類課程門數的要求，可得約束：

第二塊約束條件是課號為3，4，5，6，8，9的這些課程有先修課程的限制，因此可以建立如下約束條件：

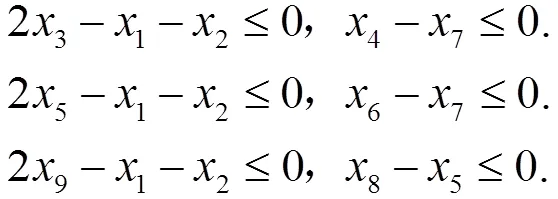
由式（1）（2）（3）就可以得到選課最少情況下的數學模型：

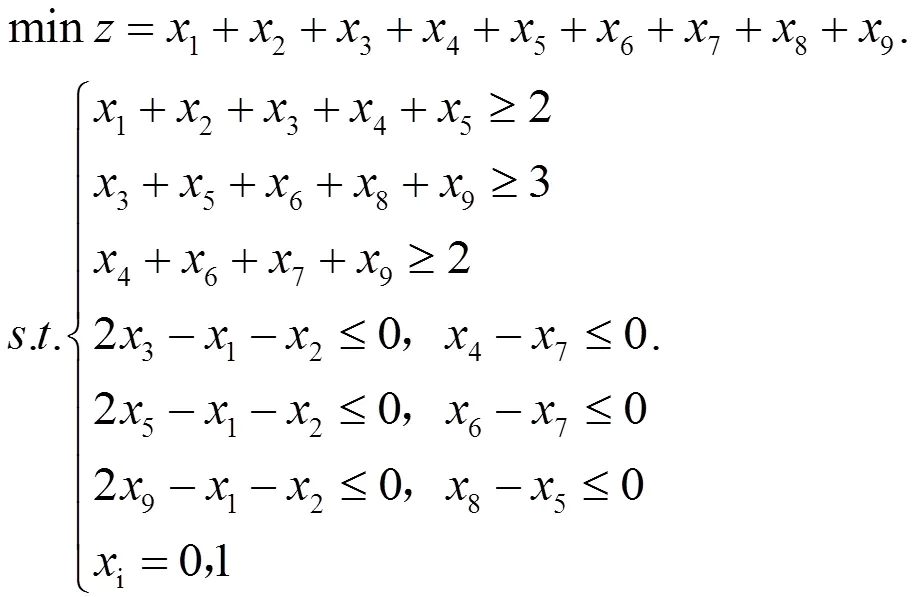
在這個過程中，學生就由數學建模的思想了解了運籌學中的0-1整數規劃的模型，知道運籌學是可以解決與他們切身相關的實際問題。但是在實際選課時，雖然做到了選課門數最少，大部分高校還有學分的要求，也就是說，雖然修的課程最少，但是學分沒有修夠，還必須進一步選修其他課程，所以問題1的最優解在考慮學分這個方面有可能是無法應用的，那么怎么才能使得我們所得到的最優解既能滿足學生需求，還能滿足學校需要呢？于是在教學過程中緊跟著提出以下問題。

問題2：如果能夠使得選修的課程盡可能少，學分盡可能多，那么該如何選擇課程呢？

其實問題2只是在問題1的基礎上增加了一個總學分的目標函數，在模型（4）的基礎上增加目標：

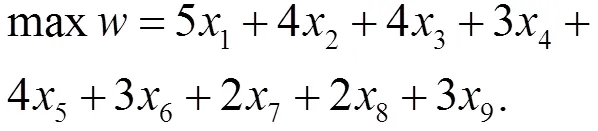
即可得到問題2數學模型：

通過上述過程，把數學建模的思想融入到了運籌學中的整數規劃的教學過程中，讓學生了解什么是數學建模，怎么樣方便地假設出決策變量。當模型建立完以后，可以介紹一下解決一般問題的0-1整數規劃的理論方法隱枚舉法。該法其實是將完全窮舉法進行改進，通過適當選擇初值來減少窮舉的過程。為了更進一步提高學生的計算機應用能力，繼續指導學生利用Lingo軟件進行編程來求出結果，從而驗證理論方法的正確性，特別地將問題2解決方法作了調整。問題2是一個多目標規劃問題，在解決問題2時需要將多目標規劃改為單目標規劃，主要做法是將其中一個目標函數整體取相反數，與另外一個目標相加就可以得到單目標規劃問題，例如目標可以改成max－或者min－.表2是利用Lingo軟件編程得到的問題1和問題2的結果。

表2 Lingo給出的選課策略

選課策略選課門數總學分 問題1數學分析、高等代數、最優化方法，計算機模擬、計算機編程、數學實驗622 問題2數學分析、高等代數、最優化方法、數據結構、應用統計、計算機模擬、計算機編程、預測理論、數學實驗931

3 結束語

本文主要通過運籌學中0-1整數規劃的一個“選課策略”案例，融入數學建模的思想，建立了一般的0-1整數規劃模型，求解方法不同于分配問題中的匈牙利法，需要用到隱枚舉法才能解決。理論方法比較復雜，又借助于Lingo軟件進行編程得到了對應不同情況下的選課策略，這樣既讓學生對理論方法有所了解，還可以提高學生的計算機軟件的應用能力。在平時的運籌學課程教學過程中，運籌學的每一塊教學內容都可以啟發學生去尋找一些實際案例，通過案例運用運籌學中對應章節的內容進行建模，再用對應的理論算法進行求解，并通過Lingo軟件進行編程求解。實踐證明，教師利用這樣的理念進行教學，有利于提高學生解決實際問題的能力和計算機應用能力，還可以激發學生學習數學的積極性，這樣的案例教學法還可以應用到其他很多課程的教學中去。

［1］胡運權.運籌學基礎及應用［M］.第6版.北京：高等教育出版社，2014.

［2］李大潛.將數學建模思想融入數學主干課程［J］.中國大學數學，2006，22（1）：3-7.

［3］田寶單，姚許乾，陳寧.數學建模思想在常微分方程教學中的應用［J］.高師理科學刊，2017，37（6）：67-69.

［4］譚永基.將數學建模思想融入通識教育數學核心課程［J］.高等數學研究，2009，12（2）：8-12.

［5］蘇紅畏.二本院校的《運籌學》課程教學改革研究［J］.教育教學論壇，2013（21）：48-50.

［6］陳娜.二本院校數學類專業運籌學課程教學改革探索［J］.當代教育理論與實踐，2015，7（6）：56-58.

［7］楊茂盛，孔凡樓，張煒.以科研促進運籌學教學改革與探索［J］.西安建筑科技大學學報（社會科學版），2006，25（6）：52-54.

［8］胡勝發，劉桂真.國家精品課程運籌學的教學改革與實踐［J］.中國大學教學，2006（7）：9-10.

季海波（1981—），男，江蘇南通人，碩士，講師，研究方向為極限理論。

2017年江蘇省高等教育教改研究項目（2017JSJG278）；宿遷學院教改項目（sqc2018jg06）

2095－6835（2018）23－0134－02

O13；G642.0

A

10.15913/j.cnki.kjycx.2018.23.134

〔編輯：王霞〕