探究柯西不等式在數學競賽的重要性

代紅軍 孔德宏

（云南師范大學 云南昆明 650500）

一、柯西不等式內容

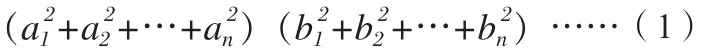
二、柯西不等式的二次函數證法

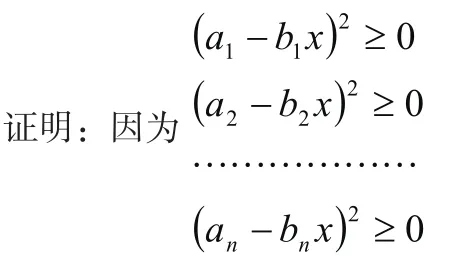
所以把上列n個不等式相加得

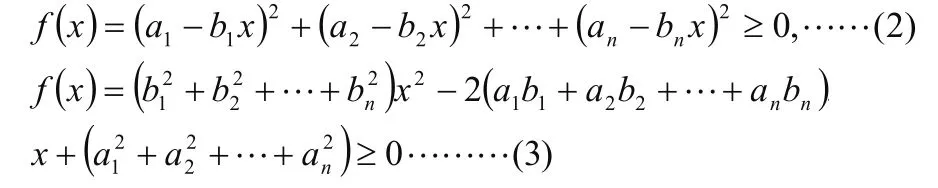
當b1=b2=… =bn=0時，已經研究。

∴f(x)是關于x的一元二次函數，∴f(x)=0方程判別式△≤0

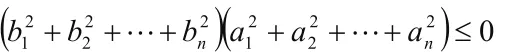
下面研究（1）式取等號的情形

若（1）式取等號，則△=0，于是由（3）知方程f(x)=0有兩個相等的實數根，即x=k,代入（2）得

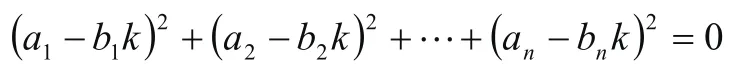
所以從兩方面證明了柯西不等式，在高考和數學競賽中，柯西不等式主要解決最值問題、取得最值時滿足的條件及推到其他重要的不等式。

柯西不等式應用特點：①構造兩組數，即兩組數對應乘積的完全平方不大于這兩組數平方和之積，由于這點柯西不等式的地位就凸顯出來了，可以培養和考察學生的創造性思維，與新課程標準相適應，所以柯西不等式依然在高中教材中以向量的方式出現。②從柯西不等式的二次函數證法發現，其實在初中階段，可以有意識地講解柯西不等式的內容，學生也能接受。所以全國初中數學聯賽與全國高中數學聯賽都在考查柯西不等式，柯西不等式可以拓展初中的知識視野。

三、柯西不等式的運用

證法一：（常用證法）

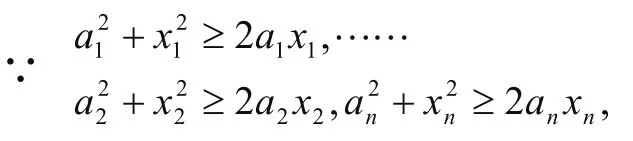
把上面n個不等式相加，得

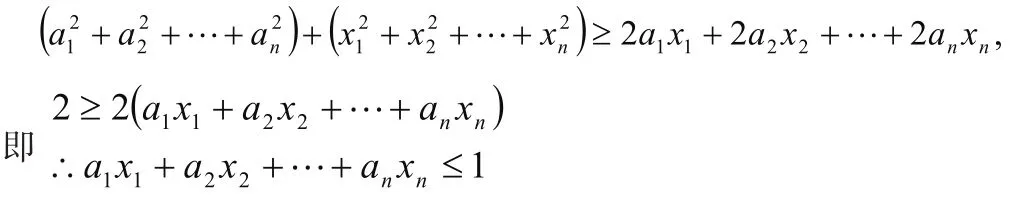
證法二：（柯西不等式證法）

分析要證明的不等式左邊，不難發現需要構造兩組數；構造怎樣的兩組數？從已知條件和要證明不等式右邊已經暗示，需要構造：

由柯西不等式（1）有

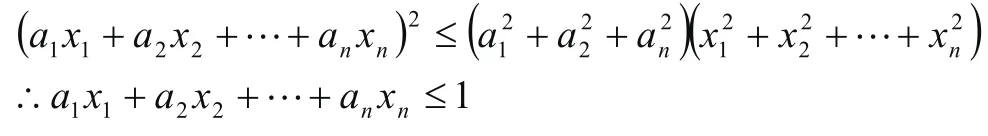
小結：對照兩種證法，不難發現證法二，思考簡潔，善于入手；證法一需要分析不等式的內部結構，不容易尋找。

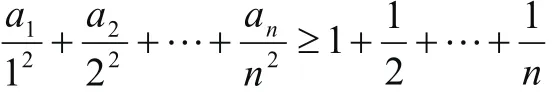
分析：上不等式可寫為

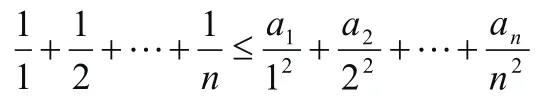
構造如下兩組數：

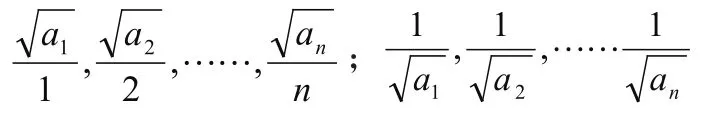
由柯西不等式（A），有

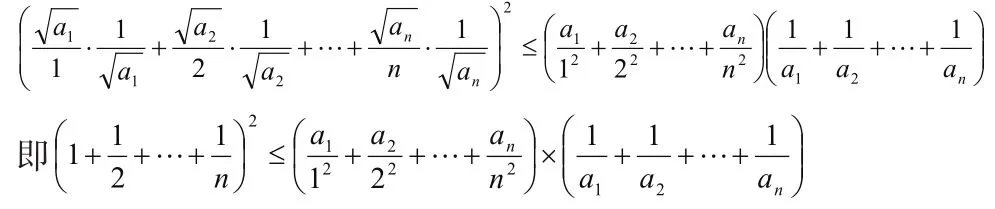
怎樣證明上一不等式呢？

因為a1，a2，……an是不相同的正整數，實數集是有序集，所以設a1，a2，……an，是從小到大排列的正整數，于是有

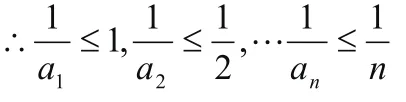
利用同方向的不等式具有可加性，有

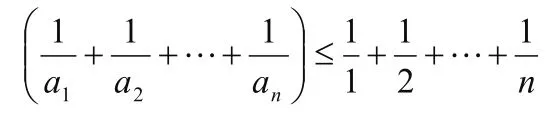
根據放縮法

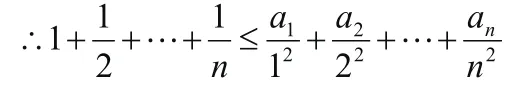
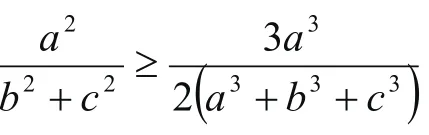
下面作出證明，由均值不等式

(a3+b3+b3)+ (a3+c3+c3)≥3a(b2+c2)，

即2(a3+b3+c3)≥3a(b2+c2)，稍加整理即為①式，證畢，回到原題。

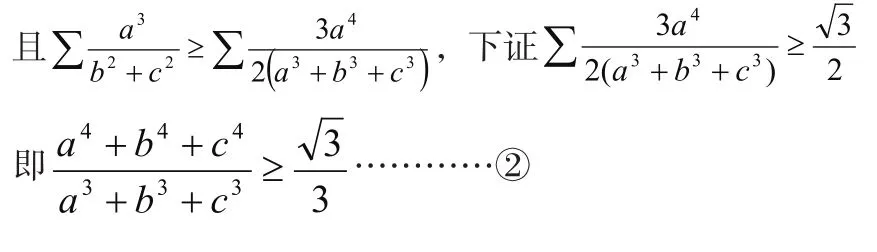
由柯西不等式

(ak+1+bk+1+ck+1) (ak?1+bk?1+ck?1)≥(ak+bk+ck)2

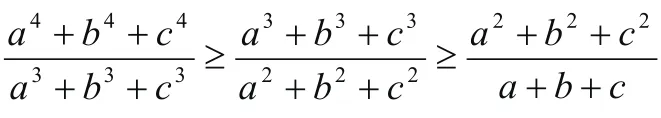
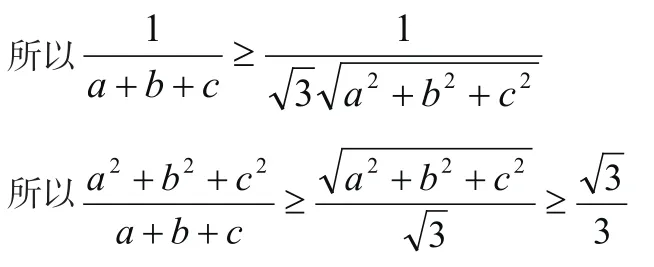
故②得證，故原不等式成立。

四、結論

柯西不等式的特點主要涉及兩組數，作用在于證明常用不等式，關鍵在于能否構造出需要的兩組數，應用范圍廣，涉及高考題、競賽題和高等數學等，是出題人所青睞的對象。