對特征值分析法在地區電網穩定分析中的運用初探
國網安徽省電力有限公司安慶供電公司 桂前進 羅利榮 徐瑞翔 劉少凡
隨著社會經濟的不斷發展,我國電網發展速度越來越快,對地區電網的穩定性進行分析有著重要的意義,而將特征值分析法應用于其中,能夠有效的分析電網的穩定性。基于此,本文通過對地區電網穩定的具體內容進行分析,從構建特征值分析法數學模型,實現特征分析、應用特征值靈敏度、多運行方式下的特征值分析等方面論述特征值分析法在地區電網穩定分析中的運用。
前言:我國國民經濟的增長,對電力能源需求不斷增加,使得智能電網的建設規模不斷擴大,對地區電網的安全穩定運行有了更高的標準。這種情況下,需要我們不僅要加強對電網整體穩定性進行研究,還要對地區電網穩定性進行詳細的分析。在電力系統中,一旦各個發電機組之間產生功角穩定問題,會導致該地區發生大面積停電事故,對人們的生活和企業的生產有著非常大的影響。
1.地區電網穩定分析的內容
對電網穩定性進行分析是保證電力系統正常穩定運行的基礎。在分析過程中,其穩定判定依據、分析方法、數學模型的建立有很多種方法,其中功角穩定與電網穩定有著密切的聯系。相關行業專家根據功角穩定性特點,為電網穩定性分析劃歸了具體內容。分別為動態穩定分析、靜態穩定分析、暫態穩定分析以及電壓崩潰等。1)動態穩定分析。動態穩定分析主要是利用分析法中的線性微分方程對調節器動態和電氣元件運行動態進行分析,判別電網的穩定性。2)靜態穩定分析。靜態穩定分析主要是指對動態系統進行簡化,具體來講就是設定一個理想的調節環境,如在勵磁調節器作用下,暫態電勢不計入計算中。然后用靜態電壓的特性對負荷進行表示,用代數方程進行表述,從而判斷出電網運行的穩定性。3)暫態穩定分析。暫態穩定分析主要是指利用非線性方程對調節器動態和元件動態的作用進行描述,從而判斷地區電網是否穩定。4)電壓崩潰的分析。電壓崩潰分析主要是指電力系統在小干擾和大干擾的作用下,電網內各個元器件和設備的無功功率的平衡狀態被打破,依靠電網中的控制措施和調節系統無法恢復,致使地區電網局部或者是整個電力系統電壓驟然下降,影響電力系統的正常工作。
2.特征值分析法在地區電網穩定分析中的運用
2.1 構建特征值分析法數學模型
在分析電網穩定過程中,特征值分析法數學模型主要是利用線性微分方程進行描述。其模型主要是將狀態變量向量與工作時間微分化,使其與狀態變量向量和非狀態向量組合成的函數表達式F相等,同時第二個條件是令狀態變量向量與非狀態向量組合成的函數表達式G等于零。特征值分析法主要是基于現代控制理論下,假設干擾較小,在運行點處將描述電網動態行為的公式線性化,以此來消除非狀態變量,從而得到狀態矩陣,線性化的狀態公式為dX/dt=AX,其中X代表狀態變量向量;A代表狀態矩陣。
2.2 特征分析的實現
在特征值分析法數學模型構建完成之后,通過對狀態矩陣特征值進行求解便能夠判斷出電網的穩定性。在對電網進行特征分析過程中,其分析程序是以插入式模型建設技術進行的,將所有的網絡方程和電網元件轉化為傳輸模塊,然后使之混合,形成一個整體的空間狀態方程。在實現特征分析時,由于地區電網的規模都不是很大,矩陣的狀態維數大多數都是低于200階的,因此利用QR算法是最為有效的,不會出現“維數災”。QR算法收斂速度快、數值精確度高,且能夠在短時間分析出電網的特征值。電網穩定問題主要表現在電網的低頻振蕩,在分析電網特征值過程中,振蕩模式與共軛復特征值相對應,其特征值用λ=α+jβ表示。其中α代表模式特征值λ的實部,主要對振蕩幅度增減進行反映,在電網穩定分析中,α必須保證小于0,同時其絕對值如果越大,振蕩的衰減幅度就會越大,表示電網的穩定性越好;而β代表的是特征值的虛部,通常情況下,低頻振蕩頻率在0.1-2.5Hz范圍內,因此,β的取值大約在0.628-15.7rad/s之間。利用α和β對特征值的阻尼比進行定義,其阻尼比ε為α與α和β平方和的平方根之間的比值。在分析中,如果阻尼比越大,說明振蕩衰減會越來越快,從而反映出電網的穩定性。
2.3 特征值靈敏度的應用
特征值分析法在地區電網穩定性分析中的運用過程中,最為主要的性質就是電網參數變化時,其特征值也會變化,即特征值能夠靈敏的感知參數變化。應用特征值靈敏度,參數的調整和選擇更加方便,從而使電網由不穩定狀態轉向未定狀態,提高電網的穩定性。在應用特征值靈敏度時,利用上述計算公式將電網不穩定根源分析出來,確定電網系統運行參數的極限數值,如輸電線路的功率。同時特征值靈敏度還可以用于PSS(電網穩定性)的參數設置和選址中。通過對振蕩模式和共軛復特征值進行計算,可以得到這兩種特征值的靈敏度,分別為參數中阻尼比的靈敏度?ε/?K和參數中特征值實部的靈敏度?α/?K。然后以電網各個節點導納矩陣和電壓矩陣為特征值中間變量,計算特征值對參數的一、二階靈敏度表達式。將一、二階靈敏度表達式與參數中阻尼比靈敏度和特征值實部靈敏度相結合。這樣在電網穩定性分析中,可以得到特征值對控制器參數、網絡參數(如變壓器分接頭、線路電抗等)、運行參數(如各個節點的功率)的敏感程度,從而分析出電網的穩定性。
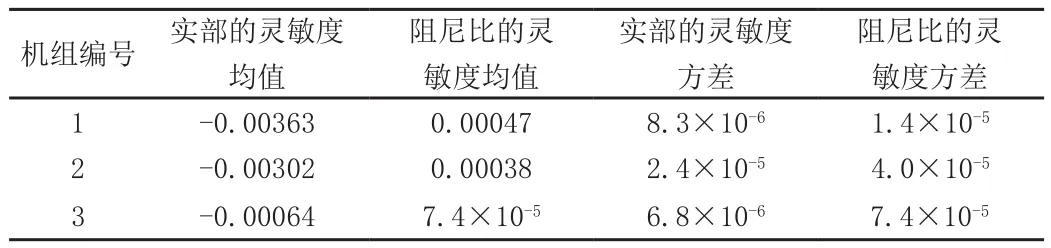
表一 機組PSS增益的靈敏度均值與方差
2.4 多運行狀態下的特征值分析
在電網運行過程中,由于發電機出力和日負荷曲線經常變化,因此,電網大部分時間是處于多運行狀態下。在分析電網穩定性過程中,保留電網機組的調速系統和勵磁系統,這樣可以得到電網的狀態矩陣。由于模式特征值與共軛復特征值是實軸對稱的,因此,只需對虛部β的特征值進行分析即可。利用QR算法對特征值進行計算,在計算過程中獲取電網中各個系統中的特征值分布,如圖一。經過計算可以得出,電網在多運行狀態下其狀態矩陣中的全部特征值實部都小于0,同時各個振蕩模式中都有與其相對應的阻尼比。因此,在電網多運行狀態下,地區電網系統的穩定性都會受到小干擾的影響。同時地區電網系統的矩陣狀態維數比較低,利用特征值分析法從靈敏度相應的執行時間、形成狀態矩陣、求解特征值等方面入手,對電網進行分析。通常情況下,多運行狀態特征值分析的時間不會超過30s,極大的滿足了電網在線分析的相關需求。

圖一 多運行狀態下電網特征值的總體分布情況
3.結論
綜上所述,用電負荷的需求日益增長,使得電網安全穩定運行要求更高,需要對其進行細致的分析。經過上文分析可得,特征值分析法在地區電網穩定分析中的應用過程中,要構建特征值分析模型,以此模型為基礎,利用QR算法,將實部靈敏度和阻尼比靈敏度計算出來。利用靈敏度分析電網的總體運行情況,得出電網特征值的分布情況,從而分析出電網的穩定性。

