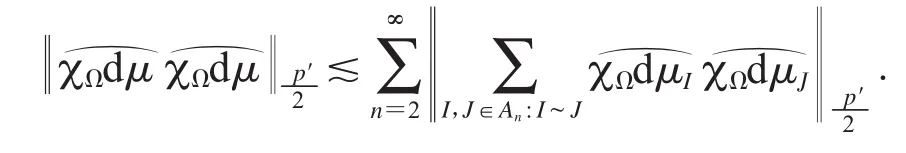橢球面的傅立葉限制性問題
范美玲
(汕頭大學理學院,廣東 汕頭 515063)
0 引言
傅立葉限制性問題的研究一直是調和分析中的熱點之一.1967年,E.M.Stein提出對于給定的Lp可積函數f,限制f的傅立葉變換?到n-1維球面S上,則(A<CB,其中C為常數,在此簡記為,A?B)成立當且僅當,這個問題后來被稱之為限制性問題.Fefferman和Stein[1]證明了在n=2時除端點之外的所有情況成立,Zygmund[2]在1974年給出了端點處的證明.Cordoba[3]在1977年用不同的方法證明二維的情形是成立的.對于高維情形,雖然已經得到了很多豐富的結果,但到目前為止它仍然未被解決,其中一個較好的結果是由Tomas和Stein[4]給出的,他們證明了當 q=2 且成立.但是他們的證明充分利用L2空間的性質,對于一般的q,該方法不能推廣,而這也是限制性問題困難所在.眾所周知,傅立葉限制性問題,Kakeya極大函數問題和Bochner-Riesz求和問題等都是相互關聯的,著名數學家Wolff,Bourgain,Fefferman,Tao等在這些問題的研究上取得了一系列進展(見文獻[5]),與其相關的方法和技巧已經廣泛應用于PDE,譜理論,數論等.本文是在他們研究的基礎上進一步拓廣傅立葉限制性問題的內容,我們限制f的傅立葉變換在橢球面上,給出橢球面上限制性問題對應的指標p,q所必須滿足的條件,并證明二維是成立的.
1 定理的提出
1.1 預備知識
首先我們回顧經典球面上的限制性猜測,它具體描述如下:
針對該問題,一個非常自然的想法是將球面換成橢球面,相關的結論是否還成立,這也是本文的出發點.為方便敘述,本文均假定E為下面形式的橢球面,,相對應的面測度為dσ.那么本文的主要結論如1.2.
1.2 主要結論
在該定理的基礎上,一個非常自然的想法是反過來是否成立,即下面的猜測.
猜測(橢球面的傅立葉限制性猜測)
它和球面限制性問題一樣,對于高維情形,困難依然存在,但是我們可以給出二維的證明,這也是本文的第二個主要結論.
定理2(二維的橢球面限制性定理)
2 定理1的證明
為證明定理1,先給下面的引理.
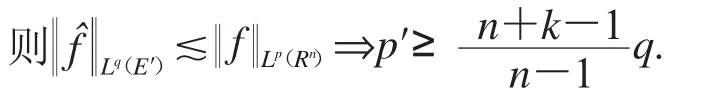
證明:證明思路是構造函數f,使f的傅立葉變換集中在E′附近.
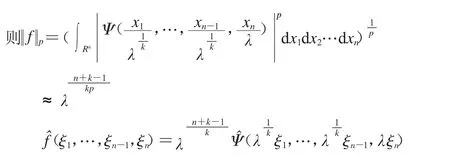
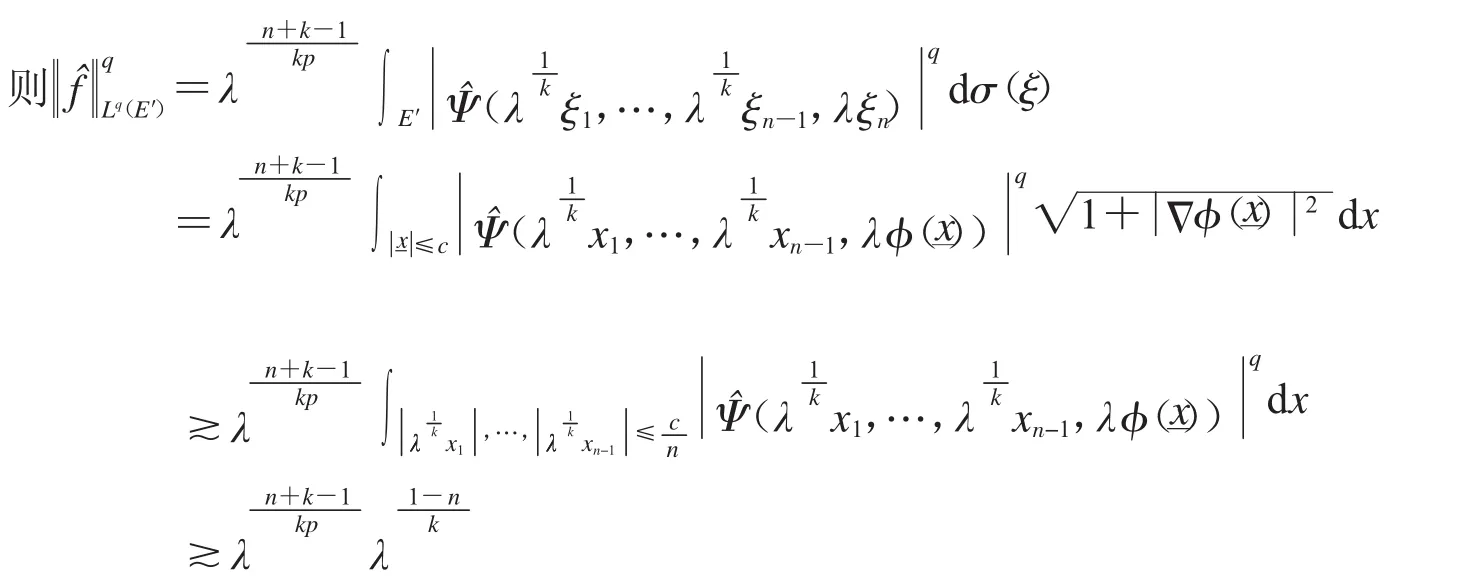
這樣就完成了引理1的證明.
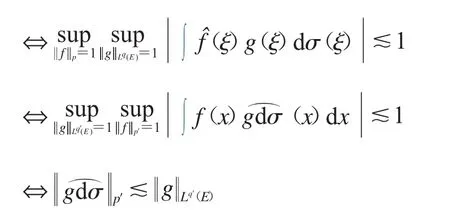
定義1:φ 是實值的 C∞(Rn)函數,a(x)是函數,定義是參數.
引理2[6]若 Ω?Rn是開集,φ(x):Ω→R 是 C∞函數,p∈Ω 且 φ(p)≠0,a(x)支撐在p的一個小鄰域內,則對任意N,
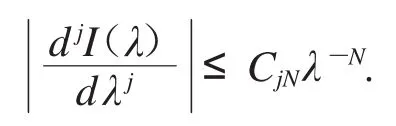
引理3[6]若Ω?Rn是開集,φ(x):Ω→R是C∞函數,在p點的Hessian矩陣H(φP)可逆,令σ是H(φP)的正負符號差,且a(x)支撐在p的一個小鄰域內,,則對于任意N,
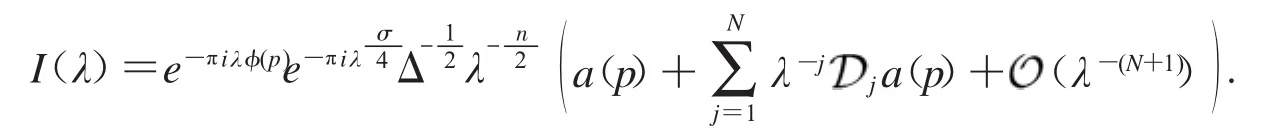


這樣就完成了定理1的證明.
3 定理2的證明
要證明定理2,我們需要下面的引理4.
引理4[8]分割圓S的弧間距和θ相互控制,若f和g支撐在S的不同θ弧上,則
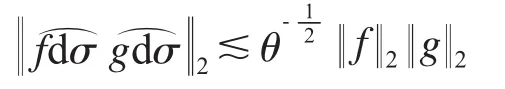
首先,要證定理2成立,我們只需證明其對偶形式成立.即證明?p′>4 且 p′≥3q.
事實上,我們可以進一步簡化指標,即在條件p′=3q>4下成立即可.
首先注意到
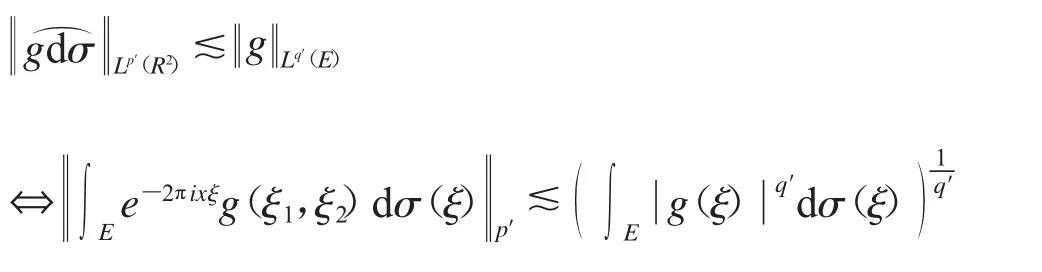
我們先把在橢圓上的積分轉化到圓上,詳細過程見式(1).
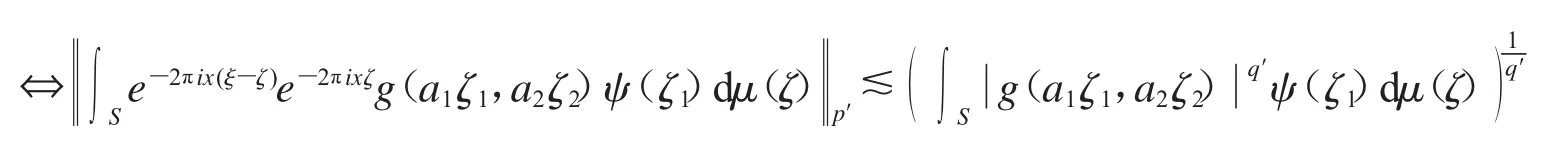
我們用Whitney分解方法[9]處理上述估計式,把圓周S平均分成2n等份,平分后所有圓弧的集合記作An.那么對任意n≥0,在n階段分割后所得的任意圓弧在n+1階段都有兩個子體.定義I~J:I,J不相鄰,I,J∈An,但存在n,使得他們的母體相鄰.那么它具有下面的性質:?x≠y,?,I~J,s.t x∈I,y∈J.從而,
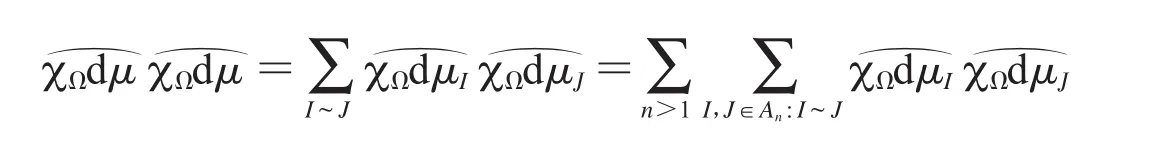
其中dμI=χ(Ix)dμ(x),dμJ=χ(Jx)dμ(x).故有