觸發式測頭預行程誤差分析與建模

馬鞍山市特種設備監督檢驗中心□王傳生 韓建彬

安 徽 工 業 大 學□馮旭剛 章家巖

1 引言

觸發式測頭系統是三坐標測量機中使用最多的測量系統，廣泛地應用于精密測量領域，但是觸發式機構中各類誤差源依舊給工件的精密檢測帶來較大困擾。Butler等人的研究表明測頭預行程誤差在測量整體誤差中的比重高達60%，并且測頭系統的觸發精度直接受到預行程變化的影響。觸發式測頭中測桿長度和觸發力大小直接影響著預行程大小，測桿長度越長產生的預行程越大，觸發力增加預行程也會增加，通過對觸發力進行理論分析和計算，可定性得出觸發力對預行程的影響。然而，預行程影響因素眾多，例如測桿旋轉位移、測桿彎曲變形位移、測頭變形位移等，為深入分析各項因素對預行程的影響，精確計算觸發式測頭預行程，有必要對觸發式測頭預行程中各項因素進行深入研究。

2 觸發式測頭

觸發式測頭工作原理等價于一個零位發訊式開關，具有結構簡單，工作可靠，測量快速，價格低廉等特點，至今仍廣泛應用于精密測量領域。觸發式測頭結構如圖1所示。圖中六個鋼球與相隔120°圓柱體構成接觸副，三個接觸副構成一個電回路，安裝在測座上的測頭在彈簧力的作用下使三個接觸副完全接觸。三坐標測量機對待測工件進行測量，測頭接觸到待測件時不會立即觸發測量信號，測頭在測量方向上持續受力，當受力大于彈簧預緊力時，至少一個接觸副脫開時發出階躍信號，光柵記錄測量信息，完成一次測量，測頭經由彈簧復位。

觸發式測頭觸發機構可近似看成兩關節機構，理論上具有五個自由度，接觸副為上部關節提供兩個自由度，使測頭能夠完成120°角度測量，測桿為下部關節，具有X、Y方向及Z軸正方向三個自由度，因此可以完成XY平面任意方向及Z軸正方向的測量，但其測量精度也會受到機構特性制約，如測桿長度、彈簧預緊力、觸發力方向等。

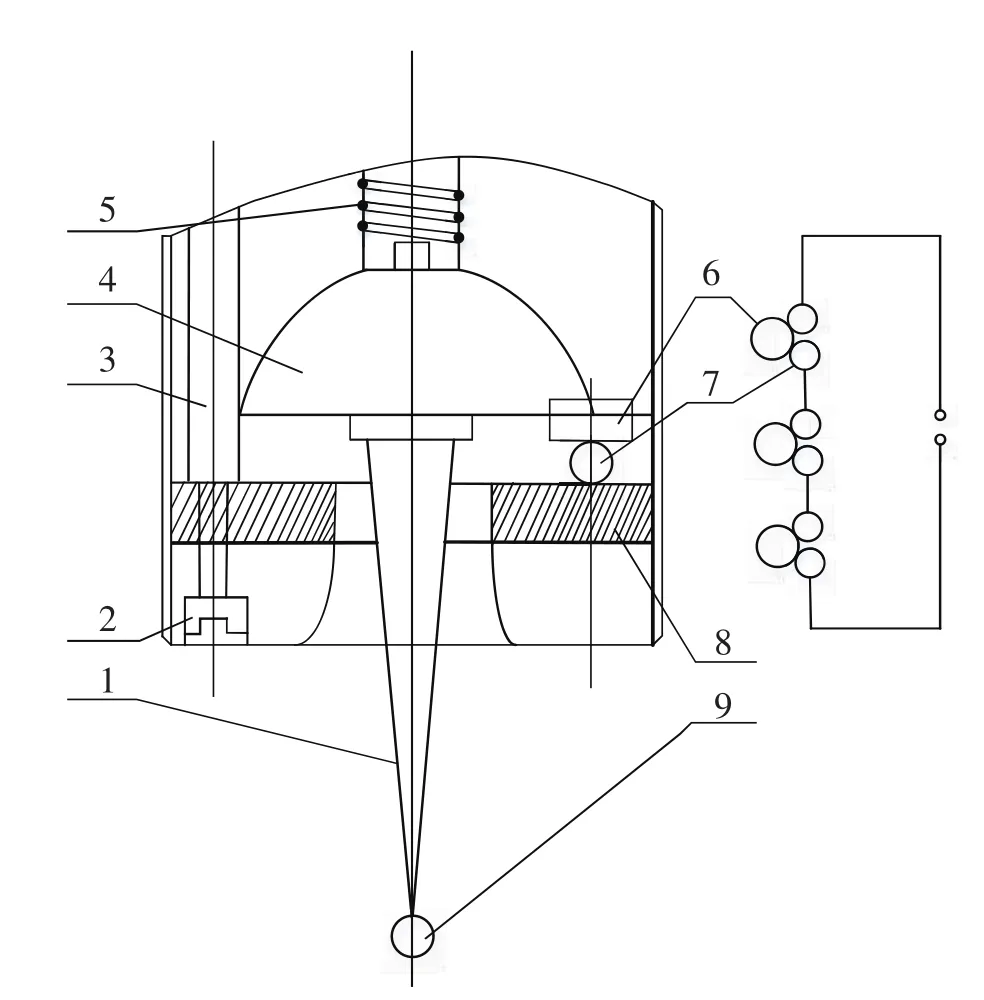
圖1 觸發式測頭結構簡圖

觸發式測頭探測待測件過程中測頭從接觸待測件到觸發測量信號這段時間內的行走距離稱為預行程，對被測工件進行測量時，觸發機構中的彈簧預緊力大小、觸發方向會使測桿、測頭發生剛性與角度偏移，從而產生預行程誤差。預行程誤差是影響三坐標測量機動態測量精度的關鍵誤差源，由于測量過程中預行程誤差是不斷變化的，有必要對觸發式測量機構進行受力分析，圍繞各項誤差因素建立數學模型，做到對誤差源的定量分析，為預行程誤差補償奠定基礎。

3 觸發機構受力分析

觸發式測頭測量待測件時受力如圖2所示。A、B、C為三個接觸副形成三腳架，對稱分布在測頭座周邊，以測桿為Z軸，垂直于測桿平面為XY平面，與向量OA軸平行且以OA方向X軸為正方向，以此建立笛卡爾空間坐標系 （xyz，i，j，k為方向向量）。忽略測桿自重對其長度的影響，測桿固定長度為L，彈簧預緊力Fs作用于測頭座中心點，方向與Z軸重合，F（θ，φ）為測頭探測待測物表面時的作用力，θ為方位角，φ為極角，此作用力的單位向量nF可表示為：

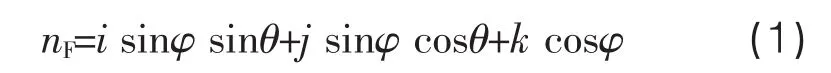
當觸發力F（θ，φ）大于彈簧預緊力時，接觸副B、C沿軸BC旋轉同時接觸副A脫離，觸發探測信號，光柵系統記錄此時測量位置。因此，觸發式測頭在測量待測物時的預行程誤差既包含了測頭旋轉位移又含有測桿彎曲位移導致的形位誤差。由于三個接觸副對稱分布，為使研究具有代表性，本文探究接觸副A脫離時的受力過程。

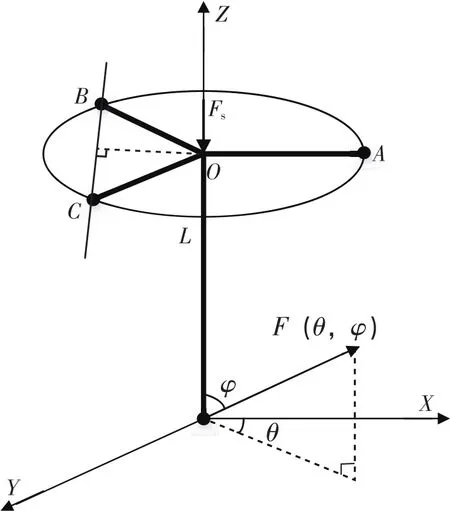
圖2 觸發式測頭受力圖

（1）測桿旋轉位移誤差

假設測頭在接觸到被測物到觸發測量信號期間不存在測桿變形、測頭與待測物表面發生滑動摩擦等其他外界干擾情況下，測頭行走的距離稱為測桿旋轉位移，旋轉位移簡圖如圖3所示。

圖中φ為測桿旋轉角度，L′為三腳架中心到軸BC的距離，R為旋轉半徑，由此形成的旋轉位移為d，即：

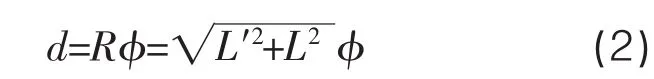
帶入笛卡爾坐標系中位移向量d可表示為：

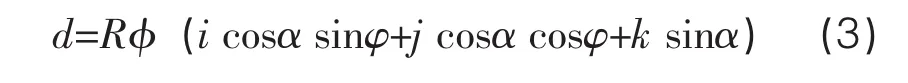
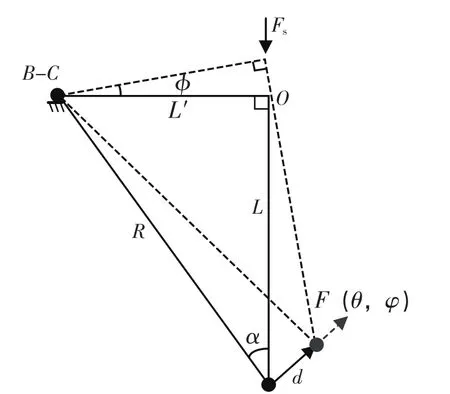
圖3 測桿旋轉位移簡圖

F（θ，φ）為測頭探測待測件時的接觸力，根據測桿旋轉位移簡圖可建立力矩平衡等式：

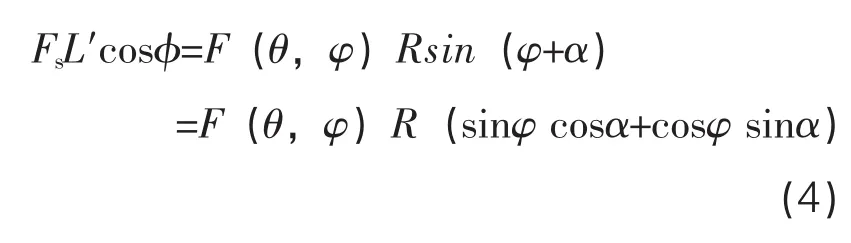
式中 cosα=L/R， sinα=L′/R， 且旋轉角度 φ特別的小，約為0，則可得：

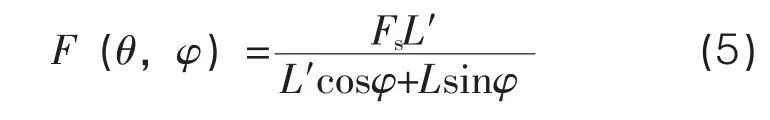
（2）測桿彎曲位移誤差

實際測量中，測桿會在接觸力F（θ，φ）的作用下發生彎曲變形，從而在測量待測件時會引入彎曲位移誤差，測桿彎曲變形簡圖如圖4所示。

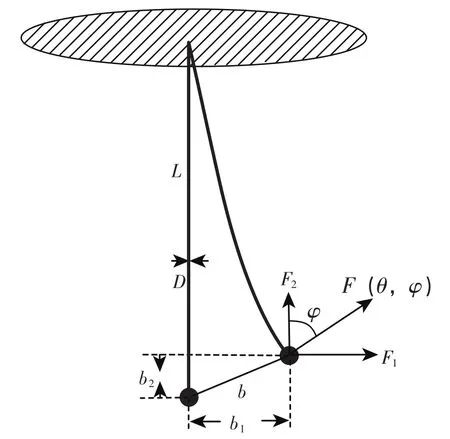
圖4 測桿彎曲變形簡圖

為便于分析可將接觸力F（θ，φ）分解為橫向和縱向力，分別為F1，F2，測桿彎曲變形位移b同理分解為b1，b2，。圖中L為測桿長度，D為測桿直徑，根據材料力學中胡克定律可得：

式中E為測桿的彈性模量，I為轉動慣量。因 F1=F （θ， φ） sinφ， F2=F （θ， φ） cosφ， 可得：

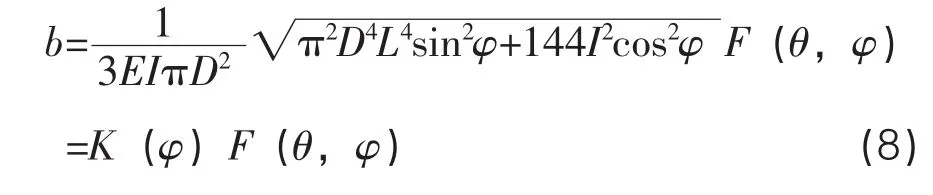
（3）測頭接觸變形誤差

當測頭測量待測件時，測頭會因接觸力的作用下產生畸變，從而測量結果會引入測頭變形誤差s。

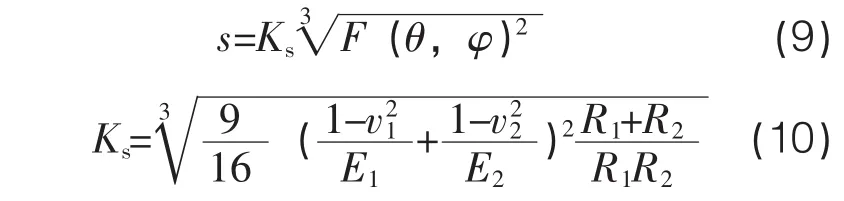
式中E1，E2分別為紅寶石測頭和待測工件的彈性模量，v1，v2分別為它們的泊松比，R1，R2分別為測頭半徑和待測工件表面曲率半徑，若待測工件表面為平面，則R2趨近于正無窮。

4 預行程函數

通過以上分析可得到預行程：P=d+b+s，即根據公式 （2）， （5）， （8）， （9） 可得：

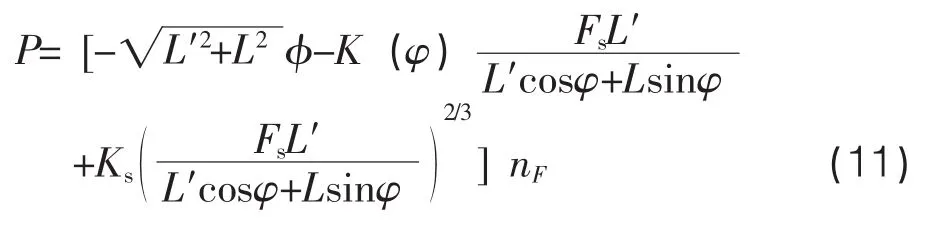
公式 （11）即為觸發瞬間預行程函數模型，實驗中紅寶石測頭彈性模量E1為150Pa，泊松比 v1為 0.1，待測工件彈性模量 E2為220Pa，泊松比v2為0.285，測桿轉動慣量I為0.0000000125 （m·kg·s2），彈簧預緊力 Fs=0.5N， D=0.002m，L′=0.02m， L=0.05m， 則仿真結果如表1所示。

由預行程函數得出的仿真結果可看出，在相同角度下測量時，測桿的彎曲位移誤差則在預行程誤差中占據較大比重；當測頭從不同方向測量同一被測物時得到不同的數據，此特性被稱為觸發式測頭預行程的各向異性。

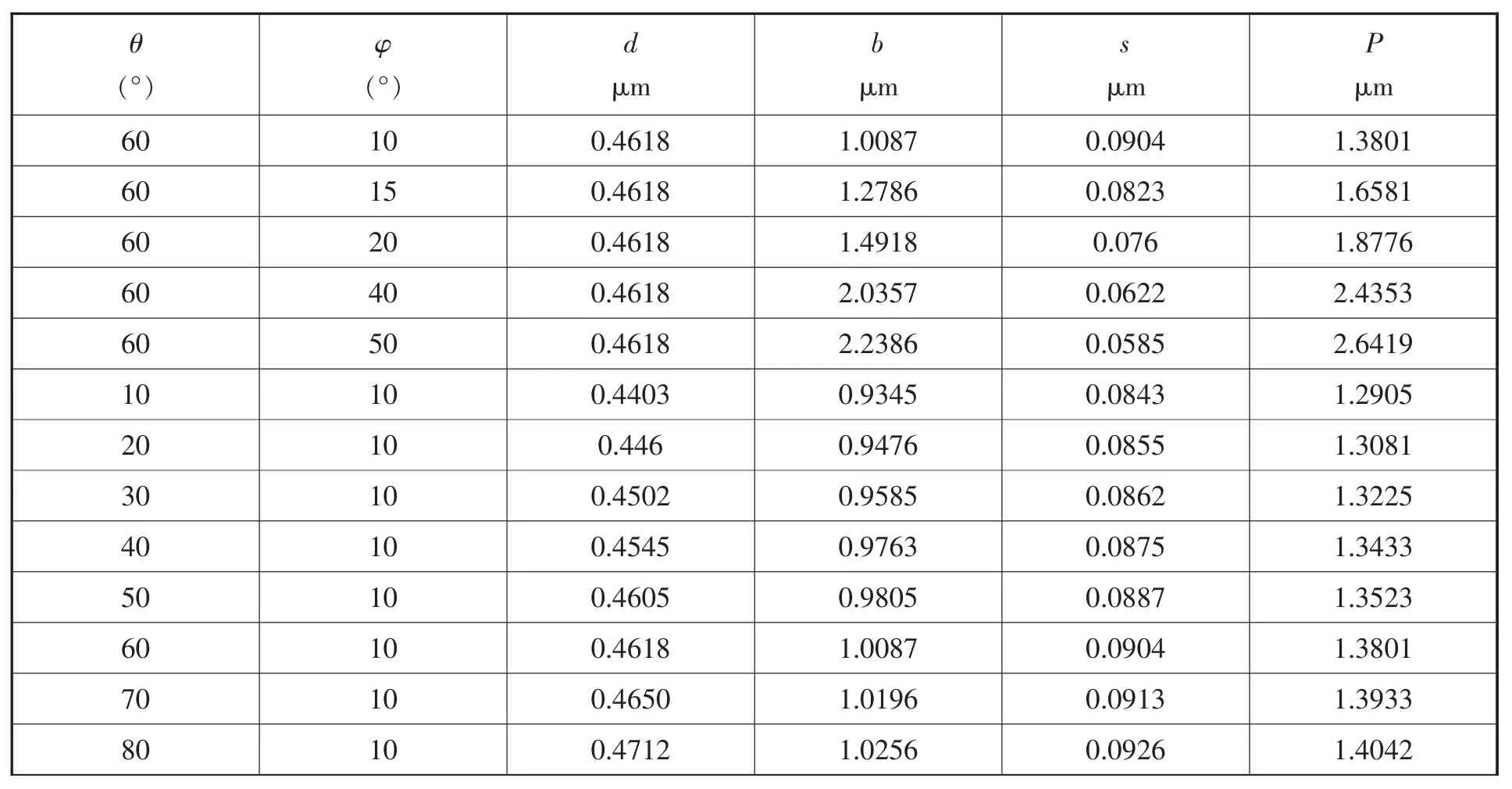
表1 預行程仿真結果

5 總結

接觸式測頭結構受力分析得出了預行程數學模型，對預行程誤差補償具有重要的意義，但同時預行程還會受到測頭運行速度、觸發力等影響，為得到更加精確的數學模型還需對觸發式測頭進一步研究。