離散需求下的藥品庫存控制模型研究

陳桂芳，石榮麗 （廣東藥科大學，廣東 廣州 510006）

1 研究背景

藥品作為特殊商品之一，其供銷的管理不僅影響著醫藥企業的運營發展，更與人們的健康息息相關。隨著醫藥衛生體系改革的不斷深入，醫藥費用居高不下，藥品價格體系混亂，藥品流通效率低下等問題越來越突出。為此，政府先后推出了《關于印發推進藥品價格改革意見的通知》、《國務院關于印發“十三五”深化基藥衛生體制改革規劃的通知》、《關于在公立醫院醫療機構藥品采購中推行“兩票制”的實施意見（試行）》等文件，分別從藥品價格、藥品流通等方面對藥品進行管制。然而這些政策的實施并不能有效解決“看病難、看病貴”、藥品價格虛高等問題。我國現有的醫藥企業約有8 000多家，市場競爭尤為激烈。藥品價格的決定是由政府和市場共同合作來完成的，而影響藥品價格主要有兩個因素：一個是藥品的成本，包括藥品的生產成本和研發成本等；另一個是物流成本，包括運輸成本和庫存成本等。研究表明[1]，庫存和運輸是成本消耗最大的物流活動，其成本約占物流總成本的三分之一到三分之二之間。庫存作為供求之間的緩沖器，一方面，使生產和物流更靈活；另一方面，保證產品對顧客的可得性。由此可見，面對政府政策的調控和市場的激烈競爭，對藥品庫存管理的研究有著重大的意義，優化藥品庫存結構、提高藥品倉庫有效利用率，才是醫藥企業降低成本、增加利潤、提高市場占有率的關鍵因素。

2 相關文獻綜述

庫存管理是許多行業運營績效的核心，由于其在實踐中的重要性，庫存管理一直是運籌學研究的熱點。從1915年Harris提出著名的經濟訂貨批量公式（EOQ模型）開始，開創了庫存模型理論的新時代。到了20世紀50年代，隨著運籌學、數量統計學等理論的應用，對庫存問題的研究也逐步形成了庫存理論，稱為“存儲論”。1953年，Whitin T.M撰寫了《庫存管理的理論》；1958年，Arrow K.J.等撰寫了《庫存和生產的數學理論研究》；1959年，Moran P.A.P撰寫了《倉儲理論》。此后，庫存理論變成了運籌學中的一個獨立分支，并根據需求的數量特征，將庫存管理模型分為確定性需求和隨機性需求，并對不同需求的庫存模型進行了廣泛深入的研究。

2.1 確定性需求庫存管理模型

從1915年Harris提出的EOQ模型開始，對于需求確定性的庫存管理問題的研究已較為完善。Goyal[2]提出了一種確定需求率的有限范圍庫存問題的經濟訂單量的方法。Ghare P M，Misra R，Shah Y K和Tadikamalla P等學者[3-6]在EOQ模型基礎上對易變質物品的庫存管理問題做了不同程度的研究，在他們的研究中，需求被假設為常數。Zeng Y[7]推導了具有確定性需求的多級梯庫存控制模型，并通過實例證明了2的整數冪的有效性。季金震[8]假設需求確定的情況下，建立由一個生產企業、一個配送公司和多個零售企業組成的多級供應鏈的多級庫存模型，求得到成本最小化的庫存控制模型的目標函數，使得整個供應鏈庫存整體最優。唐飛[9]假設需求和生產率為固定常數，提出只生產一種產品時，采用零售商占主導的寄售庫存策略，以減少供應商和零售商的總成本。趙英會[10]通過理論分析和定量分析，研究EOQ模型在中小制造企業中的優化和應用，該模型中需求量假設為已知常數。

2.2 隨機性需求庫存管理模型

對于隨機性需求庫存管理的研究，部分學者是在確定性需求庫存管理研究的基礎上進行的，并得到一定的成果。Goyal[11]在文獻[2]的基礎上提出了在一定需求變化的情況下改進庫存問題最優解的方法，并通過算例說明了該方法的有效性。Chang等[12]在經典的EOQ模型基礎上，研究部分短缺量和時變需求對經濟訂貨批量的影響，并通過數值算例說明該庫存模型的有效性。

此外，Karlin[13]提出一種動態庫存模型，在該模型中，需求分布可隨時期變化而變化。在連續的變化時期內，每個階段的最優策略的特征是一個單獨的臨界值。Song等[14]提出了一個需求率隨經濟波動或者隨產品生命周期變化而變化的庫存模型，并求出了最優策略的一些基本特征。馬士華[15]等分別考慮確定需求量和隨機需求量的情況下，建立提前期隨機的庫存控制模型。劉天亮[16]假設彈性需求下，針對是否采用替代策略情況下分別建立庫存模型并進行仿真研究。劉崢[17]等假設隨機需求下，通過比較雙渠道供應鏈下制造商和零售商的獨立庫存模型和聯合庫存模型的供應鏈成本，得到供應鏈聯合庫存模型成本更低。陳丹丹等[18]基于離散需求下，分別建立缺貨點在前和變質點在前的兩種庫存控制模型，并求解出易變質物品的最優缺貨點和最低庫存總成本，得出變質點在前的庫存總成本比缺貨點在前要低的結論。

綜上可見，無論是確定需求庫存管理的研究還是隨機需求庫存管理的研究都已較為完善。但是，在隨機需求的庫存管理中，學者們對離散需求下的庫存模型研究相對較少，且仍在不斷發展和積累中。本文考慮藥品需求為離散隨機變量，建立離散需求下的藥品庫存模型，采用（s,S）庫存策略和邊際分析法，確定其最低總成本下的最佳訂貨點和最優庫存量，從而實現優化醫藥企業庫存管理的目的。

3 離散需求下的藥品庫存模型建立和求解

3.1 符號與假定

為了更好地完成醫藥企業的生產銷售計劃，減少資源的浪費，提高藥品倉庫的有效利用率，針對藥品經營企業建模，模型假設條件如下：

（1） 藥品需求量r為離散隨機變量，可能取值為：r1,r2,r3,…,rn（ri＜ri+1，i=1,2,…,n-1 ），且ri的分布律已知。需求量r的概率為P（r），且

（2）允許缺貨，每周期初開始補貨，補貨能瞬時完成。

（3）C1為每次訂購費用，包括運輸費、保險費以及裝卸費等；C2為單位藥品存儲成本；C3為單位藥品缺貨成本；k為藥品單價；s為訂貨點；S為最大庫存量。

（4） 采用（s,S）庫存策略，即：當初始庫存量為I，訂貨點為s，若I＞s，則不對庫存進行補充；若I≤s，則對庫存進行補充，補充庫存量為Q，Q=S-I，補充后達到最大庫存量S，藥品庫存消耗途徑如圖1。

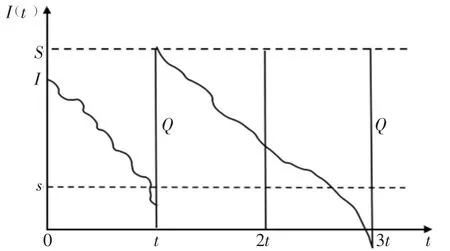
圖1 藥品庫存消耗途徑

3.2 模型的建立與最優解分析

本模型采用（s,S）庫存策略，當I≤s時，需要對庫存進行補充，庫存量由I補充到S，此時，本周期總成本=訂購成本+儲存成本+缺貨成本，其函數為：

在本周期的藥品銷售中，目的是求解出最經濟的最大庫存量S以及最佳訂貨點s，使得總成本C（s,S）期望值最小。由于需求量r是離散隨機變量，是r1,r2,…,rn中的一個，因此訂貨點s和最大庫存量S的取值也應是r1,r2,…,rn中的一個。令S=Si=ri（i=1,2,…,n），由于C（Si）是離散的，故采用邊際分析法，考察 ΔC（Si）：

由于（C1+C2）ΔSi＞0且F（Si）是關于i的嚴格單調遞增函數，因此 ΔC（Si）和［F（Si）-N］同號，且都是關于i的嚴格單調遞增。由于缺貨成本C3至少包括失去銷售機會的損失，且售價一般高于成本，則有：

在實際銷售中，一般P（r1）和P（rn）都比較小，設F（S1）=P（r1）＜N，F（Sn-1）=1-P（rn）＞N，即P（rn）＜1-N。此時則有：

由于 ΔC（S1）＜0，ΔC（Sn-1）＞0，且 ΔC（Si）具有關于i的嚴格單調遞增性質，由此可知，隨著i的增加，ΔC（Si）先取負值，然后變為正值。即C（Si）隨著i的增加，先減少，再增加，有最小值。因此，假設最優庫存量S*為：S*=Si=，要求出最小C（Si）值，則C（Si）應同時滿足不等式組：

將不等式（2）詳細寫出來得：

綜合以上兩式得：

確定最優庫存量S*后，現要確定訂貨點s。當I＞s時，不需要訂貨，此時，本周期總成本=儲存成本+缺貨成本，其函數為：

根據訂貨點s的意義，當周期初始庫存量I=s時，不訂貨的期望總成本應當不超過訂貨的期望總成本。則訂貨點s應滿足以下不等式：

整理得：

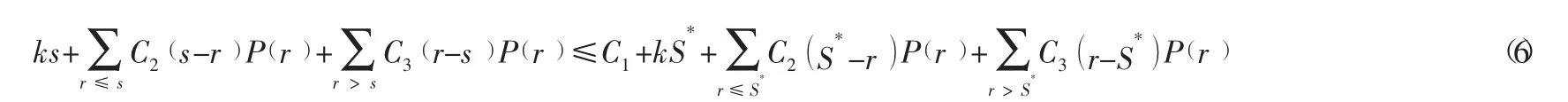
當s=S*時，不等式（6） 明顯成立，但根據最佳訂貨點s*的3個性質：①s*≤S*；②s*需滿足不等式（6）；③s*是所有滿足不等式（6）中最小。由于需求為離散的隨機變量，所以訂貨點s的取值也是r1,r2,…,rn中的一個，令s分別取值為：r1,r2,…,rn，按從小到大的順序代入不等式（6）中，則第一個滿足不等式（6）的ri為最佳訂貨點s*。

4 算例分析

假設藥店銷售某種藥品，單價為30元/盒，訂購費用為200元/次，每盒藥品存儲費用為10元/月，藥品缺貨成本為60元/盒，該藥品每月需求率如表1，根據上述的藥品庫存模型，求出該藥品最優的訂購策略。

表1 藥品需求概率表

設本周期初始庫存量I=0≤s，將上述數據代入所建模型可得：

先計算：

再計算：

顯然，左邊＞右邊，公式（6） 不成立。

同理，再將s=50，S*=70代入公式（6） 得：

左邊=3 185；右邊=2 995，左邊＞右邊，公式（6）仍不成立。

再將s=60，S*=70代入公式（6） 得：

左邊=2 955；右邊=2 995，左邊＜右邊，公式（6）成立，所以最佳訂貨點s*=60，因此該藥店應采取（s,S）=（60,70）的庫存策略，即初始庫存水平低于或等于60盒時，需要訂貨補充，最優補充量Q*=S*-I=70盒。

5 結論與討論

本文提出了需求為離散隨機變量的藥品庫存模型，從該模型的結構上看，推算出最低期望總成本下的最大庫存量以及最佳訂貨點尤為關鍵，再根據實際初始庫存量確定是否需要訂貨以及最優訂貨量，最后通過算例分析對該模型進行驗證，得到該藥品最低總成本的庫存策略為（60,70）。由于本模型是采用（s,S）庫存策略，所以在藥品儲存時可以分兩堆存放，一堆數量為訂貨點s的量，其余放另一堆。平時取后一堆以滿足需求，當取完后一堆，需要取前一堆時，則在周期末選擇訂貨；如果到了周期末，前一堆仍未動用，則本周期不訂貨。采用此策略可以在實際盤點中更容易確定是否需要訂貨，從而提高工作效率。