逆向思維的假設解題
張海燕 符云錦

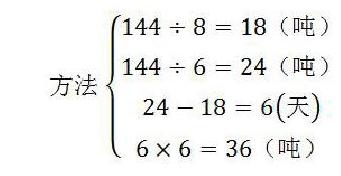

摘要:小學應用題解題能力是鍛煉學生的學識水平,解析小學應用題的思維是關鍵,用逆向思維方法解題是深入挖掘學生大腦,能更好地培養和提升學生數學水平的綜合能力。
關鍵詞:應用題;逆向思維;解題
小學應用題的解題能力是小學階段必須掌握的數學能力,也是新課標的重要內容及要求。因而解析應用題的思維能力是培養小學生必不可少的一項教學內容。在解應用題時,教師必須要注重學生的分析能力的培養,特別是應用題的正常分析能力,要善于引導學生進行正確分析理解題意,從而獲得解題的思路和方法。
一般來說,我們按照正常的思路來分析的話,首先應從應用題所描述的事情來分析,要弄清事件的來龍去脈,搞清楚時間得發展過程;然后從題意中找到已知量及量之間的關系,還要找到題意中所要求的是什么或者是怎樣的判斷;最后根據分子得出來的量及量之間的關系進行列式計算,從而獲得解答。
按照正常的思路進行解題,是每名學生必須掌握的應用題解題方法,是教師必備課。但是,有時按照正常思路解題,目的卻不是很清楚,分析到完都不知道題目所求上網量或者判斷與已知條件是怎樣的直接關系,因此就需要逆向思維進行分析。首先,要從題目所求的量或者判斷入手,找到需要的量或者需要的兩個判斷的量;然后,根據這些需要的量,再去尋找與他們有著直接或間接的相關量,當然這些相關量可以是題目已經給出的,也可以是從題目中求出的;最后,在反序一下,就可以得出題目的解法。
用逆向思維方法解題是深入挖掘學生大腦、激發思維的重要手段,同時也是考驗學生對所學知識的掌握情況,對所學知識的遷移能力,對日常生活中的應用分析能力,更大地鍛煉學生的綜合應用能力。下面舉個例子來分析。
某沙場有甲、乙兩堆沙子各144噸,甲堆沙子每天運走8噸,乙堆沙子每天運走6噸。問當甲堆沙子運完時,乙堆沙子還剩多少噸?
按照正常的思路來分析,甲堆沙子每天運走8噸,我們可以算出:144÷8=18(天),可知甲堆沙子運完需要18天,這是乙堆沙子運走的噸數為:6×18=108(噸),乙堆沙子還剩36噸沒有運走,這種解法列式為:
按照逆向思維來分析,當甲堆沙子運完時,乙堆沙子還剩多少噸?于是,我們就必須知道,乙堆沙子已經運走了多少噸。從題意中可以得出,乙堆沙子每天運走6噸,那么我們只需知道乙堆沙子運了多少天即可,這時我們想到,甲堆沙子剛好運完,再從題意又知甲、乙兩堆沙子運走的時間天數是相同的,所以只要把甲堆沙子運完所花的時間算出來,問題就得解。而甲堆沙子每天運走8噸,共是144噸,不難算出甲堆沙子運完所花的時間。我們反序下,可以得出與方法①同樣的列式計算。
此外,我們還可以得出方法②的列式計算:
方法②解釋為:甲堆沙子運完需要18天,乙堆沙子運完需要24天,乙堆沙子運完要比甲堆沙子多運6天,而乙堆沙子每天運6噸,當甲堆沙子運完時,乙堆沙子運完還需要6天,所以剩下的沙子就是剩下6天所要運的沙子。
在課堂上,學生除了用方法①、②外,還出現了第三種方法,列式計算為:
該學生又不能解釋方法③的解義,解釋不通計算的結果,但方法③確實是正確的。那么方法③應該怎樣理解呢?
我們知道,方法③的第一步和第二步與方法①、②一樣好理解,先是算出甲堆沙子運完時需要18天,甲堆沙子每天比乙堆沙子多運走2噸,關鍵是第三步算式不好理解。第三步從算式上理解為在甲堆沙子運完時,甲堆沙子比乙堆沙子多運多少噸?如果算式有實際意義的話,那么第三步算式應理解為當甲堆沙子運完時,甲堆沙子比乙堆沙子多運的噸數和一堆沙子剩下的噸數相等,問題的關鍵就在這里,是否真的相等尚待理解,從字意來理解確實理解不同。
我們再想想,甲、乙兩堆沙子的重量是相等的,所以回答是肯定的。我們換種思路來思考:反過來,如果乙堆沙子每天運走8噸沙子的話,那么當甲堆沙子運完時,乙堆沙子應該也會全部運完,而實際上乙沙子每天是少運了2噸,也就是說,乙堆沙子每天剩下2噸沒有運走,所以,當甲堆沙子運完時,乙堆沙子少運了2×18=36噸,這剛好就是乙堆沙子剩下沒有運走的沙子!這種理解符合實際,也容易理解。因此,方法③也是正確的。
綜上所述,方法③是換種思考方式來分析,我們把“甲堆沙子比乙堆沙子每天多運2噸”進行逆向思維假設成“如果乙堆沙子每天也能運走8噸下,而實際上乙堆沙子每天只能運走6噸,剩下2噸沙子沒有運走”,導致了“當甲堆沙子運完時的18天內,乙堆沙子就剩下了36噸沙子沒有運完”,方法③得以理解。為此,在解答小學應用題時,學生不妨把已知條件逆向假設一下,也許很難理解的解題思路就變得容易理解了。
參考文獻:
[1]義務教育課程標準實驗教科書.四年級數學上冊[M].北京:人民教育出版社,2017

