搖擺自復位高墩高階效應研究

張育智

(西南交通大學 土木工程學院，成都 610031)

采用延性方法設計橋墩時，通過在橋墩與承臺或(和)橋墩與主梁的連接部位進行塑性鉸設計，使橋墩在大地震時在上述位置形成塑性鉸，一方面塑性鉸的出現會降低結構剛度，延長結構周期，從而可以減小輸入到結構中的地震動能量；另一方面塑性鉸的出現將消耗大量已經輸入結構的地震動能量，減小結構整體的地震動響應。雖然延性設計能夠實現“大震不倒”的性能要求，但由于塑性鉸的形成，使結構發生了永久性的殘余變形，導致了結構的損傷，這直接導致震后結構功能的恢復非常困難。由于經濟和安全原因，大量按照延性方法設計的結構往往在震后被拆除而非修復，這在造成巨大經濟損失的同時，給人民的震后生活帶來了極大不便。

隨著研究的逐步深入，研究者越來越清晰地意識到控制結構地震殘余位移的重要性[1-5]。在20世紀90年代便有研究者提出了震后無損傷結構設計方法[6]。該方法的核心思想是將結構設計成具有搖擺自復位能力的結構。對于橋墩來說，搖擺自復位橋墩是指: 將橋墩與承臺或(和)橋墩與主梁之間連續的鋼筋斷開，放松橋墩在上述部位受到的轉角約束，在發生大地震時，橋墩能夠在上述部位形成搖擺界面，利用橋墩的搖擺降低對橋墩抗彎能力的地震需求，使結構在大地震中仍能處于彈性工作狀態，且在地震結束后，結構能夠自動恢復至初始位置。震后無損傷結構設計的目的是: 結構的地震內力并非隨地震動強度的增大而持續大幅增大，而是將結構的地震內力控制在一定范圍內，這樣就可以最大程度地消除地震動不確定性導致結構損傷的可能性，即使地震動強度比設計結構時所采用的地震動強度高，結構仍然不會在地震過程中發生損傷。

在地震過程中，根部形成塑性鉸的剪力墻可以視為搖擺結構，在對搖擺剪力墻的研究過程中[7-10]，研究者發現利用非線性時程計算得到的根部剪力比按照一階模態分布的水平地震力作用下計算出的根部剪力大，前者約為后者的1.4～4倍；且結構將在除根部以外的其他位置形成第2個塑性鉸，隨著研究的深入，研究者認識到這是由于搖擺自復位結構的高階效應導致的——雖然1階模態效應在結構發生搖擺后便不會繼續增大，但高階模態效應可以在結構根部形成搖擺界面的邊界條件下繼續增大，這便是搖擺自復位結構中的高階效應。

為了實現震后無損傷，必須對搖擺自復位結構高階效應進行控制。為此，首先需要判斷各階模態對結構地震響應的貢獻，從而確定需要控制哪些階次的高階效應。國內對搖擺自復位結構的研究起步較晚，對搖擺自復位結構高階效應的研究尚未見報道。國外對搖擺自復位結構高階效應的研究主要針對鋼框架結構[11]，尚未見針對搖擺自復位高墩高階效應的相關研究，由于高橋墩的動力性能與鋼框架有較大差別，有關鋼框架的結果并不能直接用于高橋墩。因此，開展針對搖擺自復位高墩高階效應的研究非常必要。

1 高階模態貢獻的計算方法

Wiebe[12]采用振型參與系數、各階模態振型及加速度反應譜構造了反映各階模態貢獻的綜合指標，對搖擺自復位框架的高階振型貢獻隨著結構根部抗彎剛度變化的規律進行了研究，但該方法并不適用于對某一特定搖擺結構整個搖擺過程中各階模態振型貢獻的計算。Hasan等[13]利用模態分解法對四層搖擺自復位框架結構中各階模態貢獻進行了研究，由于概念清晰，便于理解，因此本文采用模態分解法對搖擺自復位高墩的各階模態貢獻進行分析。

模態分解法的思路是利用在線性系統中成立的模態分析方法來計算非線性搖擺自復位結構的各階模態動力響應，因此模態分解法是一種近似方法。

(1) 各階模態內力的計算。

結構各階模態引起的結構內力，包括剪力和彎矩，可以根據對結構非線性時程計算得到的等效地震荷載進行模態分解而求得。根據結構動力學[14]模態分析的相關知識，首先引入非線性多自由度結構第n階模態的等效地震靜力{fe,n(t)}

{fe,n(t)}={sn}·αn(t)

(1)

式中:αn(t)為與線性結構中的偽加速度An(t)相對應的非線性系統中第n階模態的偽加速度； {sn}為第n階模態等效地震荷載的空間分布向量

{sn}=Γn·[m]{φn}

(2)

式中：Γn為振型參與系數； [m]為結構的質量矩陣； {φn}為結構的第n階振型。

假定疊加原理對搖擺自復位結構仍然適用，則結構t時刻總的等效地震靜力{fe(t)}等于t時刻各階等效地震靜力之和，即

(3)

利用振型的正交性，將式(3)左右兩側左乘{φn}T經整理得

(4)

式中：Mn為第n階模態的廣義質量。

具體求解方法及步驟:

步驟1根據非線性時程計算的結構剪力結果可以得到t時刻結構中各節點的等效地震靜力{fe(t)}，即由相鄰單元根部剪力差組成的列向量；

步驟2由式(4)可以得到第n階模態的偽加速度αn(t)；

步驟3由式(1)計算第n階模態的等效地震靜力列向量{fe,n(t)}；

步驟4由式(5)可求得t時刻第n階模態對應的橋墩根部剪力Qn(t)

(5)

式中：fie,n(t)為t時刻i節點的等效地震靜力；m為節點數；

步驟5由式(6)可得t時刻第n階模態對應的橋墩墩底彎矩Mn(t)。

(6)

式中：hi為i節點到墩底的高度。

(2) 各階模態位移的計算。

為計算各階模態位移，需要引入與第n階模態單自由線性系統位移響應Dn(t)相對應的第n階模態單自由度非線性系統等效位移響應δn(t)。 則第n階模態的位移向量{un(t)}可以表示為

{un(t)}=Γn·{φn}·δn(t)

(7)

利用疊加原理，結構總的位移向量可以表達為

(8)

利用振型的正交性，式(8)左右兩側左乘{φn}T， 經整理可得第n階模態單自由度非線性系統的等效位移

(9)

在得到δn(t)之后， 根據式(7)便可以得到各個時刻各階模態對應的結構位移。

2 高階模態貢獻的定量指標

在由上述模態分解法求出各階模態對應的結構剪力、彎矩及位移之后，為了求解各階模態對這些結構響應的貢獻，必須給出描述各階模態貢獻的指標。以往采用的指標主要有3種。

(1) 第n階模態響應絕對值最大值|rn(t)|max與總響應絕對值最大值|rtot(t)|max之比ID1， 第n階模態貢獻計算公式見式(10)，各參數意義見圖1。

(10)

(2) 總響應最大值對應時刻tm第n階模態響應值rn(t)t=tm與總響應值rtot(t)t=tm之比ID2， 第n階模態貢獻計算公式見式(11)， 各參數意義見圖1。

(11)

(3) 第n階模態響應時程曲線與時間軸圍成面積與總響應時程曲線與時間軸圍成面積之比ID3， 第n階模態貢獻計算公式見式(12)。 其中tt是整個地震動持續時間。

(12)

上述ID1和ID2都只能反映某個時間點各階模態響應與總響應之間的比值關系，極易受到地震動隨機性的影響，不利于較完整和準確地描述各階模態對總響應的貢獻。ID3將整個地震動過程作為一個整體進行考慮，未對結構發生搖擺與未發生搖擺進行區分。而搖擺自復位結構在發生搖擺之后，其動力性能會發生變化，從而導致各階模態對總響應的貢獻發生一定的變化，因此采用ID3評價搖擺自復位結構各階模態對總響應的貢獻也存在不足。

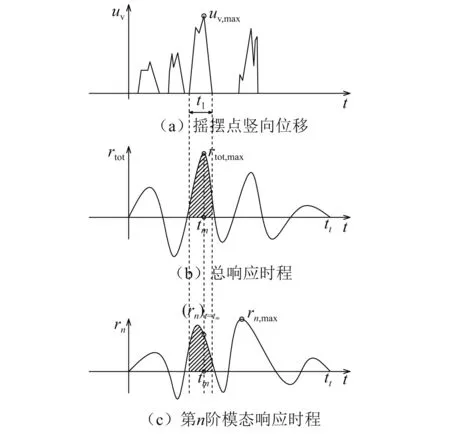
圖1 搖擺點豎向位移，總響應及第n階模態響應時程示意圖Fig.1 Sketch of rocking point vertical displacement, total and the n th mode response

由于結構發生搖擺后其動力性能會發生變化，且搖擺過程中結構響應值通常較大，為了反映搖擺結構的這一特點，各階模態貢獻指標應能反映結構發生搖擺時段內各階模態的貢獻。為此，本文作者提出ID4，即搖擺幅度最大的時間段內(圖1中t1時段)，經歸一化的各階模態響應時程曲線與時間軸所圍面積與總響應時程曲線與時間軸所圍面積的比值，見圖1中搖擺點最大豎向位移uv,max對應的陰影面積，第n階模態貢獻計算公式見式(13)。

(13)

3 計算模型介紹

本文針對某圓端形鐵路橋搖擺自復位橋墩[15]進行計算分析。橋墩的幾何尺寸如圖2所示，空心墩身高56 m，實心墩身及擴大基礎均高2 m，橋墩外壁坡度為1∶40，內壁坡度為1∶90。橋墩采用C30混凝土，上部結構的質量為7 190 kN，以集中質量形式施加在墩頂節點，橋墩擴大基礎底面，即搖擺界面，傳遞的豎向荷載為36 357 kN。本模型無耗能裝置及后張預應力，依靠重力提供自復位的恢復力。采用OpenSEES對橋墩順橋向的地震動響應進行非線性時程分析，橋墩采用彈性梁柱單元進行模擬，搖擺模型采用夏修身等[16]提出的兩彈簧模型，兩彈簧間距即為墩底擴大基礎順橋向尺寸10 m。彈簧單元剛度取為2.1×108kN/m，采用瑞利阻尼，取前2階模態的阻尼比均為5%。計算模型的示意圖見圖3。

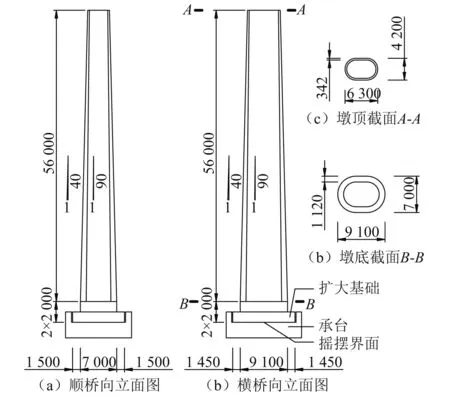
圖2 橋墩尺寸圖(單位: mm)Fig.2 Pier dimensions (unit: mm)

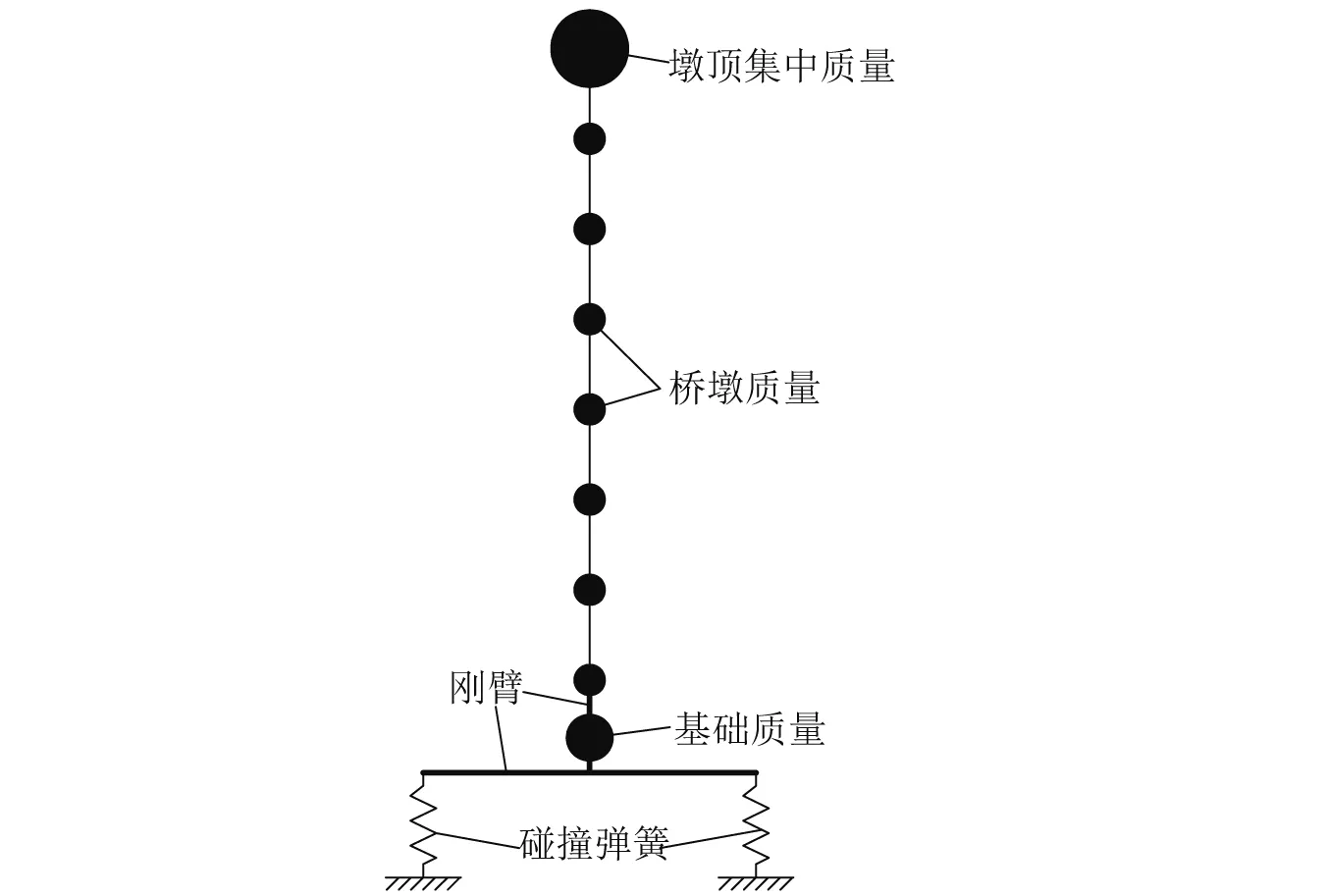
圖3 有限元模型示意圖Fig.3 Sketch of finite element model

4 地震動輸入

為考慮地震動差異性的影響，從FEMA P695遠場地震動系列中選取了7條D類場地的地震波作為輸入，相關地震動記錄的信息見表1。為了考慮地震動強度的影響，分別將地震動的峰值加速度調幅至0.2g，0.4g和0.6g。

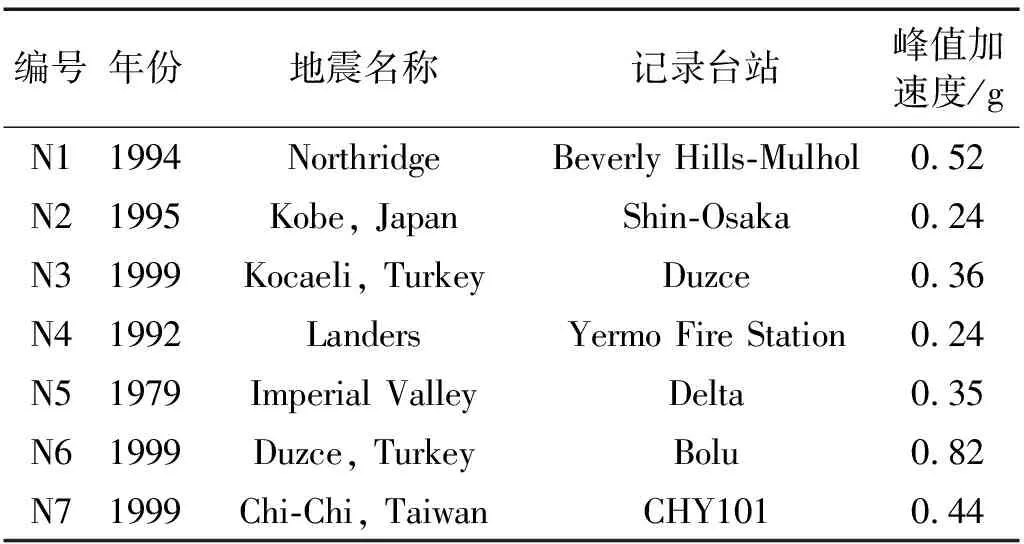
表1 地震動記錄信息Tab.1 Information for ground motion records

5 計算結果

5.1 模態分解法計算結果

由于墩底剪力對高階效應比較敏感，因此以墩底剪力為例，圖4給出峰值加速度調幅至0.4g的N1地震動記錄為輸入時，結構前4階模態與總響應的對比情況。

根據圖4并結合表2給出的指標ID3和ID4計算得到的前4階模態對墩底剪力的貢獻百分比可見: 對于墩底剪力而言，前2階模態對總響應的貢獻均較大，二者之和占總響應的80%以上；第3階模態對總響應的貢獻仍達8.8%，而第4階模態對墩底剪力的貢獻便顯著減小。

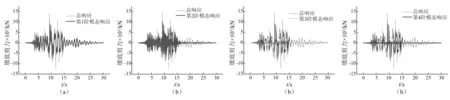
圖4 墩底剪力總響應與前4階模態對比Fig.4 Comparison of base shear for total and first four modes’ response

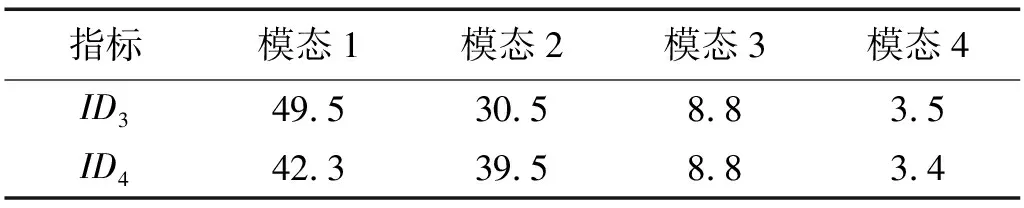
表2 前4階模態對墩底剪力貢獻比較Tab.2 Contribution comparison of base shear for first four modes%

5.2 各階模態貢獻計算結果

第2節中的指標ID1和ID2只是對結構響應最大值出現瞬時結構特性的反映，并不能充分反映各階模態對總響應的貢獻，在本研究中未采用上述2種指標。指標ID3是整個地震動作用時間范圍內各階模態對總響應的貢獻的一種度量方法，但是未對搖擺自復位結構搖擺與否加以區分，不能反映出此類結構獨有的特征。因為ID3和ID4都是歸一化的指標便于比較，因此本節給出前3階模態2種指標計算結果的對比。

5.2.1 墩底剪力計算結果

表3給出了不同地震動強度條件下2種指標計算的前3階模態對墩底剪力貢獻的平均值及變異系數。

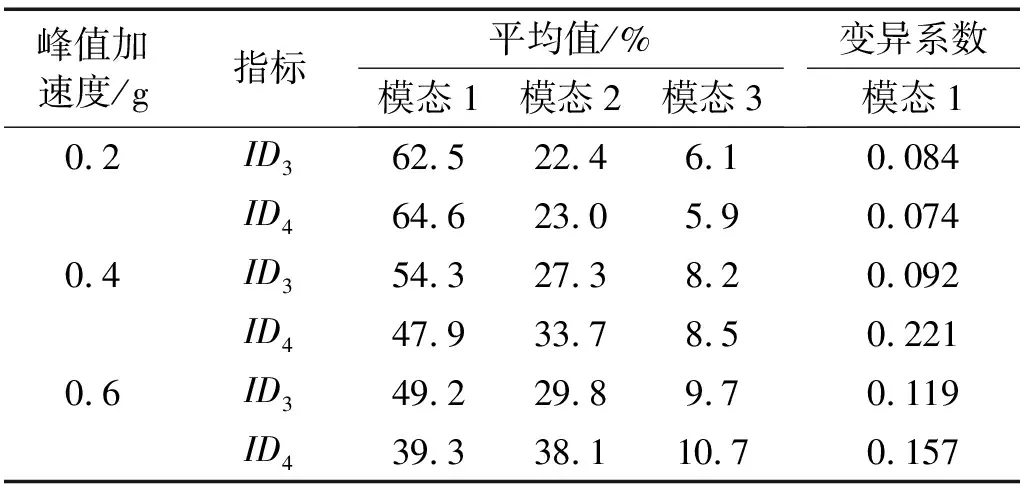
表3 不同模態對墩底剪力的貢獻對比Tab.3 Contribution comparison of base shear for different modes

由表3可得到以下規律:

(1) 隨著地震動強度的增大，第1階模態對墩底剪力的貢獻逐漸減小，而第2階和第3階模態對墩底剪力的貢獻逐漸增大，當地震動峰值加速度為0.6g時，2種指標得到的第2階模態貢獻分別已達到第1階模態貢獻的61%和97%，由此可見，高階模態對墩底剪力貢獻顯著，在進行搖擺自復位結構抗剪設計時，必須充分考慮高階效應的影響。

(2)ID3與ID4的差別隨著地震動強度的增大而增大。產生上述差異的原因是ID3和ID4分別是針對整個地震動時長和最大搖擺階段的評價，這種差異實際上反映出結構發生搖擺后各階模態貢獻與未發生搖擺時有一定的差異，這是搖擺結構特有的特性。當地震動峰值加速度為0.6g時，對比ID3與ID4的結果發現，第2階模態的貢獻分別達到第1階模態貢獻的61%和97%，采用ID3將大大低估第2階模態的貢獻。由此可見，對于搖擺自復位結構，ID4比ID3更適合評價結構響應較大的搖擺階段高階效應的貢獻。

(3)ID3的變異系數比ID4的小。這是因為隨著評價時長的縮短，計算結果越來越依賴于結構搖擺階段的響應，而搖擺階段的響應受地震動隨機性的影響較大，因而當評價從整個地震動時長縮短到最大搖擺階段時，各階模態貢獻變異系數就會增大。這實際上反映出搖擺階段各階模態貢獻受地震動變異性影響較大，在實際分析時，應該采用多條地震動計算進行計算，并利用計算結果的統計值進行評價。

5.2.2 墩底彎矩計算結果

表4給出了不同地震動強度條件下2種指標計算的前3階模態對墩底彎矩貢獻的平均值及變異系數。

由表4可見，與表3反映出的規律類似，隨著地震動強度的增大，第1階模態對墩底彎矩的貢獻逐漸減小，第2階和第3階的貢獻有所增加；ID4比ID3更能反映出各階模態貢獻隨地震動強度的變化規律。對搖擺自復位結構而言，高階模態對墩底彎矩的貢獻要小于對墩底剪力的貢獻。

表4 不同模態對墩底彎矩的貢獻對比Tab.4 Comparison of base moment for different modes

5.2.3 墩頂水平位移計算結果

表5給出了不同地震動強度條件下2種指標計算得到的前3階模態對墩頂水平位移貢獻的平均值及變異系數。

表5 不同模態對墩頂位移的貢獻對比Tab.5 Comparison of pier top displacement for different modes

由表5可見，由于結構發生搖擺后，墩頂水平位移主要都是由結構繞搖擺點的剛體轉動(即搖擺自復位結構搖擺狀態下的第1階模態)產生的，因此高階模態對搖擺自復位橋墩墩頂水平位移的貢獻很小，即使在地震動峰值加速度為0.6g的條件下，第1階模態的貢獻仍在90%左右。

6 結 論

(1) 應該采用能夠反映結構搖擺階段特性的指標ID4對搖擺自復位結構各階模態貢獻進行評價。

(2) 隨著地震動強度的加大， 1階模態的貢獻逐漸減小，而2階、3階等高階模態的貢獻逐漸增大，在結構發生搖擺后，高階模態的貢獻比搖擺前大。

(3) 對于搖擺自復位高墩，墩底剪力對高階效應最敏感，在分析時應考慮前3階的影響；墩底彎矩對高階效應較敏感，在分析時需考慮前2階模態的影響；墩頂水平位移對高階效應最不敏感，在分析時可只考慮1階模態的影響。

(4) 搖擺自復位結構高階效應控制的目標是對第2、第3階模態的控制，且以第2階模態的控制為重點。

致謝

本研究是在中央高校基本科研業務費專項資金的資助下完成的，在此表示感謝！