基于特征權值的缺失數據修復方法
鄭 潔
(貴陽職業技術學院,貴州 貴陽 550081)
近年來,數據挖掘技術得到了蓬勃的發展,人們能夠從海量的數據信息中提取或“挖掘”出有用的知識,這些知識可提供給相關領域使用,因此,將數據挖掘技術看作是信息技術自然演化的結果[1]。在現實生活中,我們面臨著各種各樣的數據問題,通常,我們將數據預處理作為進行數據挖掘的一個前期工作。缺失數據的處理問題作為數據預處理領域的一個研究熱點[2],為了能夠更加充分地利用已經搜集到的數據,對缺失數據的處理是非常必要的。
1 特征權值計算
Relief算法以類內和類間的距離作為基礎來評判該特征屬性的重要性,作為一種重要的機器學習方法,廣泛應用于數據的特征選擇、分類等方面[3],本文的研究工作是在基于Relief算法的思想上來求解屬性特征權值。
對于一個含有決策屬性的數據集,假設x是數據集合中的任一個樣本,如果x'是與同類距離最近的樣本,y是與x異類距離最近的樣本,考慮x與x',y的距離在各個特征上的投影,記為pin(a,x,x')與pout(a,x,y),其中a是屬性特征集合中的一個特征。對于連續型的數值變量,Relief算法給出了計算特征權值的規則:
其中:pin(a, x, x ')=| x -x′|, pout(a, x, y) =|x -y|,初始化特征權值wk= 1/m;對于數據集中每一個樣本數據按照公式(1)更新每一維屬性權值,即可輸出屬性集的特征權值
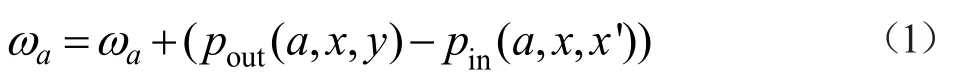
2 基于屬性權值的數據修復
在殼近鄰計算方法(Shell Neighbors Imputation,SNI)中[4],我們把每一個選擇出來的左、右近鄰對數據修復的結果影響程度看作是相同的,但實際上,由于每一維屬性的重要程度是不同的,因此,我們將特征權值引入數據填充計算,采取如下公式:

3 實驗與結果分析
3.1 預測準確率和數據缺失率
為了說明本文提出的修復方法的有效性,我們引入一個衡量預測準備率的參數:均方根誤差(Root Mean Square Error,RMSE),它的定義如下:
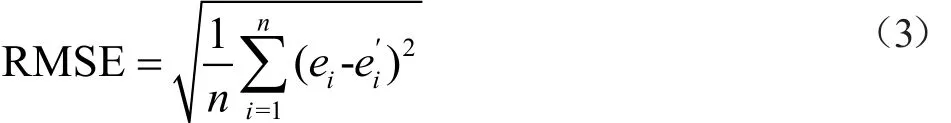
其中:ei是原來的屬性值,是填充值,n是數據集中缺失值的個數,對數據進行填充后,通過計算得出RMSE的值可以驗證數據的修復效果,RMSE的值越大,表示預測準確率就越低,即數據的修復效果越不好,相反則說明修復效果越好。
3.2 實驗方法與數據集
本章的實驗數據來源是UCI標準數據集[5]中的兩個真實數據集,為了測試預測的準確率,我們選擇完整的數據集,每次隨機地將其中部分的數據設為缺失,對其進行填充后,再與原本的值一起計算RMSE的值來比較修復效果。每一個數據集上進行500次實驗,表1是實驗數據集的基本信息。
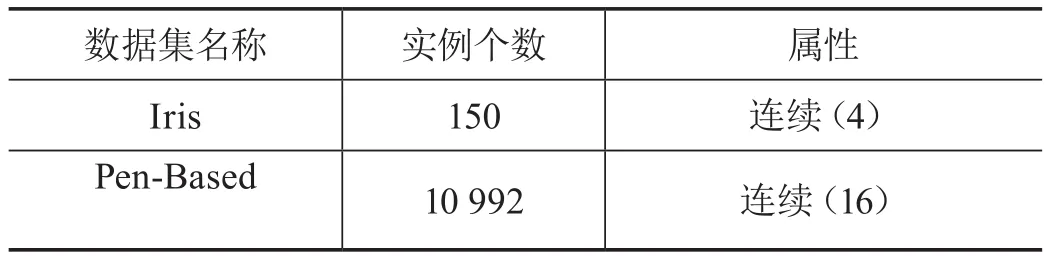
表1 數據集基本信息
3.3 實驗結果與分析
將本文提出的修復方法與殼近鄰計算方法分別在表1描述的兩個真實的UCI數據集上進行模擬實驗,結果如圖1—2所示。
根據上述實驗結果,我們可以得到以下結論:
(1)隨著數據集中數據缺失程度不斷提高,兩種填充算法計算所得的RMSE的值會逐漸增大,即數據填充準確率隨著數據缺失率的增加會逐漸降低。尤其是當數據缺失率超過20%以后,兩種算法數據修復的準確率明顯下降。
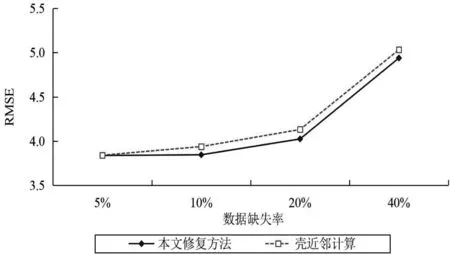
圖1 Iris數據集上的填充效果對比
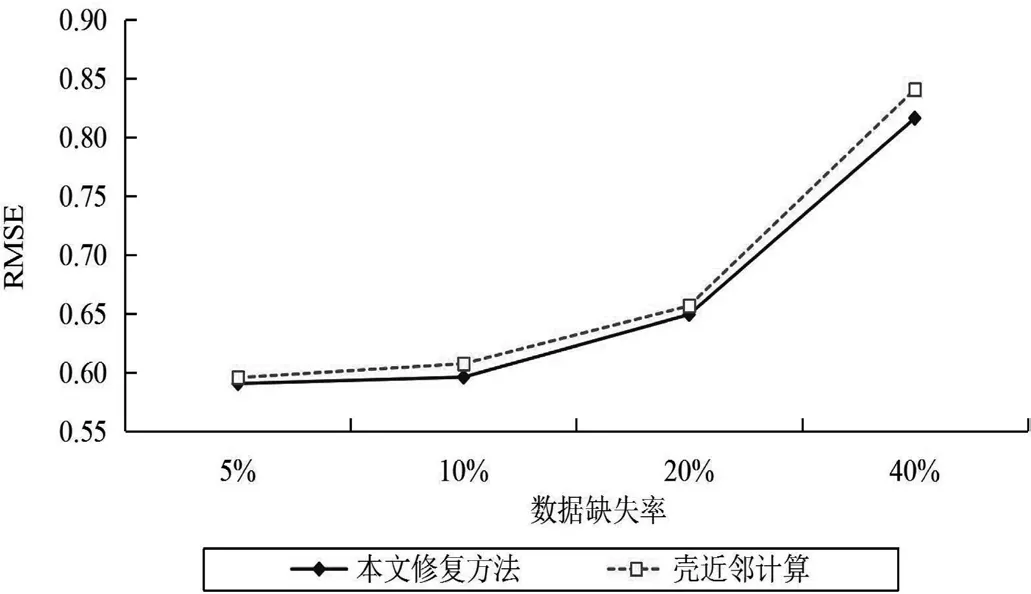
圖2 Pen-Based數據集上的效果對比
(2)在大數據集Pen-Based的RMSE值明顯小于小數據集Iris的RMSE值,也就是說,我們可以認為在數據缺失率相同的情況下,數據集越大,計算過程中可以利用的已知信息會越多,由此可能會使得缺失數據的修復準確率更高。
(3)在兩個數據集上,本文提出的方法對缺失數據修復的效果都優于SNI,由此我們可知:如果對屬性的特征權值計算合理,將其引入數據填充計算中,可以提升數據修復的效果。

