手寫體數字的K-最近鄰法識別研究

黃金海

（桂林電子科技大學 信息科技學院，廣西 桂林 541004）

在模式識別領域，對手寫體數字的識別，是許多從事圖像處理、機器學習研究人員的入門練習。其實現方法已經有許多成功的案例，王一木等[1]提出自組織映射簡化算法在硬件電路上以并行運算實現的手寫數字識別。邵虹等[2]提出基于投影定位及數字結構特征的方法識別發票印刷體數字。幸堅炬等[3]提出概率神經網絡實現mnist數據集數字的識別，并有較高的準確率。李瓊等[4]提出在特征空間中確定SVM最優核方法實現手寫數字的識別。以上實現方法都采用不同的算法實現，本文以成功識別手寫數字為出發點，提出在pyqt5環境中以K-最近鄰（K-Nearest Neighbor，KNN）分類器算法實現手寫體數字的識別。

1 KNN算法原理

在機器學習分類方法中，KNN是無監督學習中最簡單、易理解的分類算法。該思想是Cover和Hart在1968年的研究工作中提出的，它根據距離函數計算待分類樣本X和每個訓練樣本間的距離（作為相似度），選擇與待分類樣本距離最小的K個樣本作為X的K個最近鄰，最后以X的K個最近鄰中的大多數樣本所屬的類別作為X的類別[5]。

KNN算法大致包括如下3個步驟。

（1）算距離：給定測試對象，計算它與訓練集中的每個對象的距離。

（2）找鄰居：圈定距離最近的K個訓練對象，作為測試對象的近鄰。

（3）做分類：根據這K個近鄰歸屬的主要類別，來對測試對象分類。

因此，最為關鍵的就是距離的計算。一般而言，定義一個距離函數d(x,y)，需要滿足以下幾個準則。

d(x,y)=0

d(x,y)≥0

d(x,y)=d(y,x)

d(x,k)+d(k,y)≥d(x,y)

距離計算有很多方法，本文以歐幾里得距離（Euclidean distance）實現手寫體數字的識別。其計算公式如下：

2 手寫體數字圖像識別流程

手寫數字的原始圖像，可以有多種獲取方法，本文以畫圖面板寫出任意0～9的數字，并按順序以jpg格式命名數字圖像作為手寫體數字的初始樣本圖像。圖1中列舉了每個數字的兩種手寫體樣本。

當讀入數字樣本圖片時，首先對數字樣本進行圖像預處理，預處理過程包括將圖片灰度化、縮放為與訓練集同等尺寸大小32×32格式、將32×32圖片二值化并保存為txt文件。接著K值取3對新保存的txt樣本訓練；訓練完成后根據KNN多數分類法則識別顯示。流程如圖2所示。

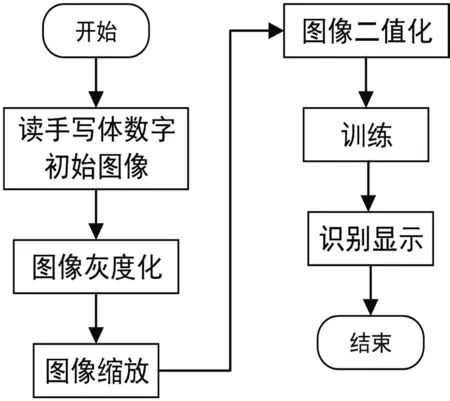
圖2 識別流程

3 數據處理

樣本的數據處理包含數字的訓練和識別兩部分。數字的訓練集和測試集分別是常用的trainingDigits和testDigits。由于數據集是已經二值化的txt文本格式，需要將32×32的測試集與訓練集分別轉換為1×1 024的一維向量，把測試集中每一個樣本分別與訓練中每個樣本進行歐幾里得距離計算，計算結果按KNN原理分類提取各個樣本標簽，分別完成預測數字和真實數字的比較。當K值分別取3，5，7，9時，其運算的正確率如表1所示。

表1 不同K值正確率

從表1中可知，當K取3時，正確率最高，達到98.99%。K取取值越大，正確率均略有下降。

4 測試分析

經過上述數據處理分析，測試集與訓練集的比較結果有高達97%以上的正確率，那么輸入前文所述的20個測試樣本，以pyqt5作為顯示界面，與訓練集中的所有樣本進行KNN運算，其測試結果如圖3所示。

圖3 KNN手寫體數字測試圖

由圖3可知，手寫體數字的KNN算法識別準確率與測試集的準確率有較大差距，20個樣本中15個正確，錯誤率高達25%。這表明，KNN算法在手寫體數字識別中的應用研究仍有待提高。

5 結語

手寫體數字的KNN算法執行效率并不高，識別準確率的提高需要更多訓練樣本集，如mnist數據集。但是，數據樣本集越多，運算的時間就會越長，其效率也會越低。工程應用中人們都希望識別能力既高效準確率又高，技術人員可以嘗試其他算法模型來完善識別效果。