基于VSG的光伏發電系統建模與仿真研究

孟 超，趙 咪，樊然然，唐文星

(石河子大學機械電氣工程學院，新疆 石河子 832000)

0 引言

近年來，隨著環境污染和化石能源短缺等問題的日益嚴重，新能源的利用已成為人們關注的焦點[1]。其中，光伏發電以其清潔、經濟等優點，得到了大力發展[2]。光伏并網發電具有很大的隨機性和波動性，會造成電壓幅值和頻率的嚴重波動，影響電網的穩定運行[3]。光伏并網采用電力電子逆變器接口，導致系統中的旋轉慣量減少，系統缺乏慣性、阻尼等特性，耐沖擊能力差。因此，當系統負荷波動或內部出現故障時，會造成系統頻率失穩和內部不穩定。在此背景下，如何通過控制變流器以實現光伏發電高效、友好的并網，是亟待解決的關鍵問題[4]。

同步發電機具有對電網天然友好的優勢，若借鑒傳統電力系統運行經驗，使并網逆變器具有類似同步發電機的特點，則可實現光伏發電的友好接入，并提高發電系統的穩定性[5]。為此，虛擬同步發電機(virtual synchronous generator,VSG)技術應運而生[6]，改善了逆變器的并網特性，向電網提供了必要的頻率和電壓支撐。其中，文獻[7] 研究了VSG控制對改善微電網頻率穩定性的作用，但未詳細介紹底層矢量并網控制算法。文獻[8] 設計了在負荷擾動條件下，自動改變慣性系數以消除功率波動的方案，但功率的波動幅值依然很大。

鑒于此，本文針對光伏發電系統，提出了一種電壓型VSG控制策略。首先，闡述了目前常用的兩種VSG類型及其原理；并分析了VSG的有功頻率控制和無功電壓控制原理，建立電壓型VSG的二階數學模型。然后，利用MATLAB/Simulink，搭建了基于VSG的光伏發電系統模型。最后，對光伏陣列的輸出特性、VSG控制策略和光伏發電系統的運行特性進行了仿真試驗。

1 VSG控制方法

1.1 VSG類型

現有VSG技術主要包括兩種技術路線。一種由魯汶大學和克勞斯塔爾工業大學提出，通過控制逆變器輸出電流dq軸分量，使新能源發電設備具備調頻調壓功能的電流控制型VSG，可以等效為一個電流源[9]，難以為系統提供電壓和頻率支撐。另一種由利物浦大學等機構提出，通過控制逆變器內電勢的幅值和相角，使新能源發電設備具備調頻調壓功能的電壓控制型VSG[10]，實現了VSG和同步發電機在物理和數學模型上的較好等效，并可實現VSG無鎖相環的自同步運行，能較好地提升母線電壓穩定性。本文選用電壓控制型VSG實現光伏發電系統的仿真分析。

1.2 VSG的本體算法

根據不同階次的同步發電機模型，可建立不同的VSG數學模型。在眾多模型中，二階模型可以完全消除同步發電機復雜的電磁耦合關系，進而實現對輸出功率的良好控制。經典二階同步發電機等值模型如圖1所示。

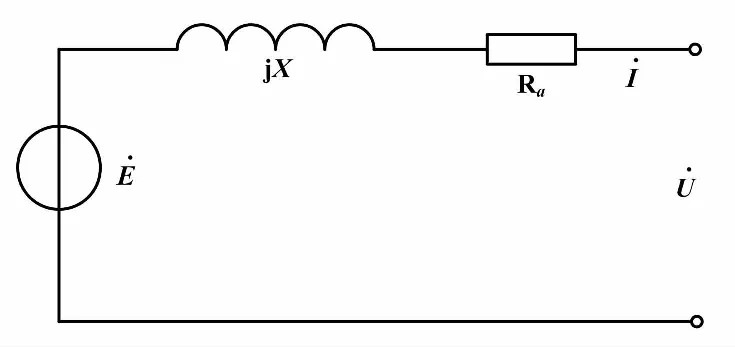
圖1 經典二階同步發電機等值模型

從圖1可得同步發電機的二階機電暫態模型[11]，如式(1)所示。

(1)

式中：E為VSG的感應電動勢；I、Ra和U分別為電樞電流、電樞電阻和電樞電壓；X為同步電抗；θ為功角；Tm和Te分別為機械轉矩和電磁轉矩；D為阻尼轉矩系數；Δω為額定角頻率與實際角頻率之差；Pm和Pe為機械功率和電磁功率；ω為額定角頻率；J為轉動慣量。

1.3 有功頻率控制

頻率是衡量電能質量的一個重要指標，因此控制系統的頻率在允許的范圍內波動，是保證電力系統穩定運行的一項基本任務。VSG的有功頻率控制實際上是模擬同步發電機的調速器來表征有功功率和系統頻率的下垂特性，使得系統的有功功率保持平衡。其控制方程如式(2)所示。

(2)

式中：P0為VSG的有功功率參考值;ω0為角速度參考值;R為下垂系數;Pe為額定有功功率。

根據式(2)可得虛擬同步發電機的有功頻率控制原理框圖，如圖2所示。

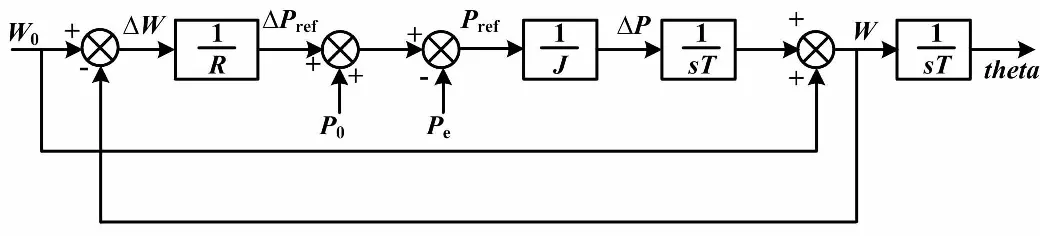
圖2 有功頻率控制原理框圖

從圖2可知，當調速器動作時，將設置的角速度參考值與系統的額定角速度進行比較，所得的角速度差值乘以調差系數后轉化為系統缺少的有功功率，再與有功功率參考值和額定有功功率作簡單運算，即可得有功功率差ΔP。調速器通過檢測ΔP來控制虛擬機械轉矩輸出，從而調節頻率。

1.4 無功電壓控制

電力系統中，電壓過高或過低都將對人身和用電設備產生重大影響。因此，保證用戶的電壓接近額定值是電力系統的另一項基本任務。VSG的無功電壓控制實際上是模擬同步發電機的勵磁控制器來實現無功功率和電壓幅值的下垂特性，使得系統的無功功率保持平衡。其控制方程如式(3)所示。

Emag=U0+K(Qn-Qe)

(3)

式中：Emag和U0分別為VSG的輸出電壓和參考電壓；K為調差系數；Qn和Qe分別為VSG的無功功率參考值和輸出的無功功率。

虛擬同步發電機的無功功率電壓控制原理如圖3所示。

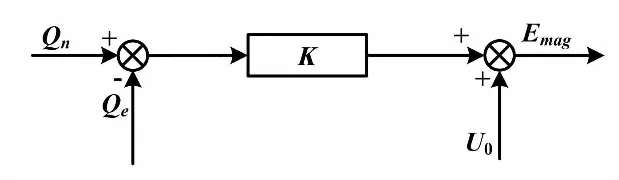
圖3 無功功率電壓控制原理框圖

通過測量得到系統某時刻的無功功率，并與設置的無功功率參考值進行比較，即可求出一個無功功率差。其差值乘以調差系數K后，可得系統的電壓差額。該差額與電壓參考值進行求和后，可得調整電壓。

2 基于VSG的光伏發電系統仿真分析

2.1 基于VSG的光伏發電系統

基于VSG的光伏發電系統主要包括：光伏陣列、BOOST電路、最大功率跟蹤(maximum power point tracking,MPPT)、脈沖寬度調制(pulse width modulation,PWM)、調速器、勵磁控制器、VSG算法、正弦脈沖寬度調制(sinusoidal pulse width modulation,SPWM)、濾波電路和負載等模塊。基于VSG的光伏發電系統結構如圖4所示。

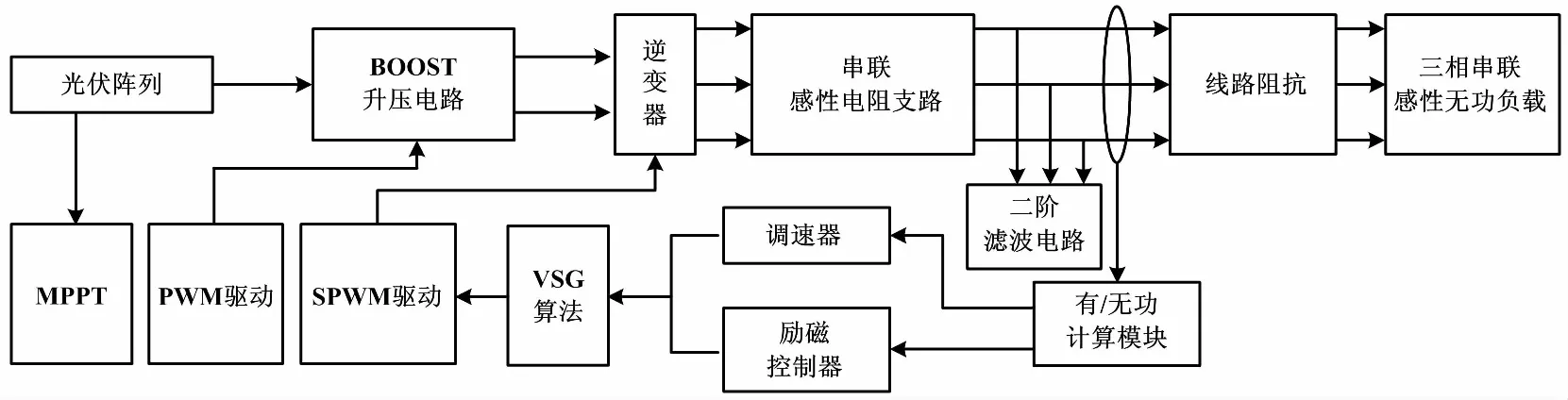
圖4 基于VSG的光伏發電系統結構圖

為了驗證控制算法的有效性，基于MATLAB/Simulink仿真平臺搭建系統仿真模型。仿真參數為：Isc=59.8 A；Im=55.6 A；Uoc=438 V；Um=360 V；直流側逆變電壓為766.5 V；額定頻率為50 Hz；濾波電感為8 mH；濾波電容為40 μF。

2.2 光伏陣列輸出特性分析

光伏陣列的輸出特性隨一天內的環境溫度(T)和光照強度(S)的變化，按照一定的規律變化[12]。

設T為25 ℃恒定不變，而S分別為1 000 W/m2、750 W/m2和500 W/m2。則當S等差減小時，光伏陣列輸出I-U和P-U特性曲線如圖5所示。

從圖5的仿真結果可知：①光伏陣列的Isc與S成正比關系，S每增加250 W/m2則Isc約增加1 A，S對開路電壓Uoc的影響不大；②電池的輸出功率P與S成正比關系，S對P的影響顯著，尤其是功率峰值點處。

設S為1 000 W/m2恒定不變，而T分別為15 ℃、25 ℃和35 ℃。則當T等差增加時，光伏陣列輸出I-U和P-U特性曲線如圖6所示。

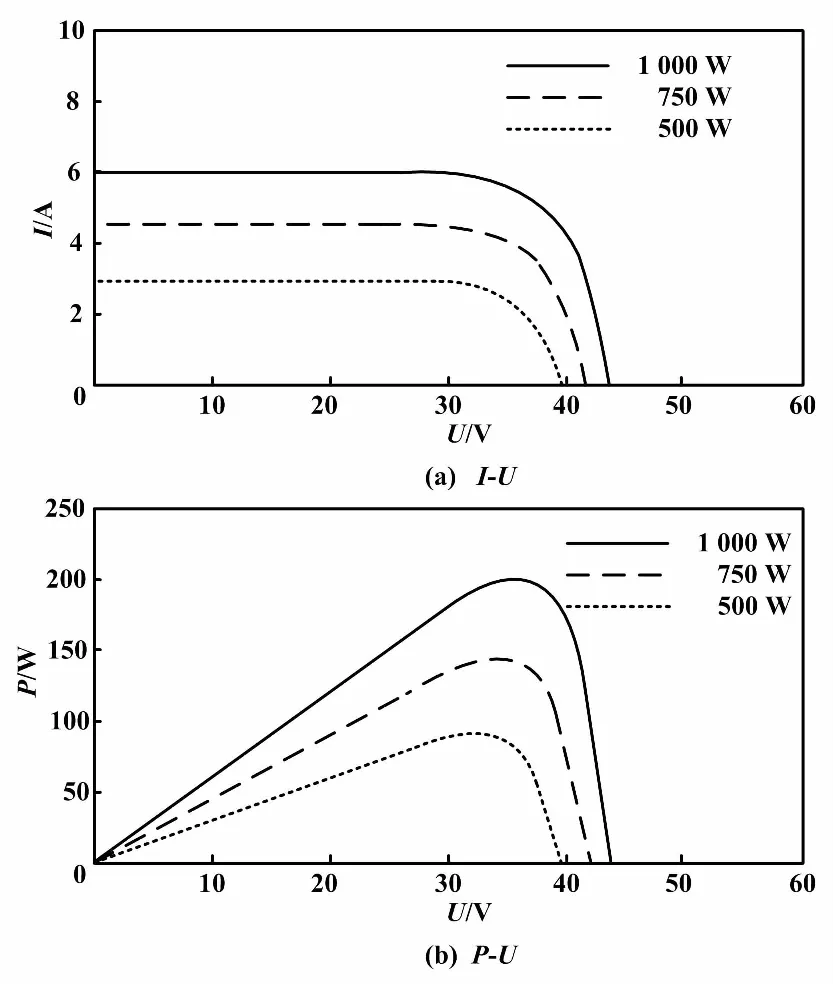
圖5 光伏陣列輸出特性曲線(S等差減小)

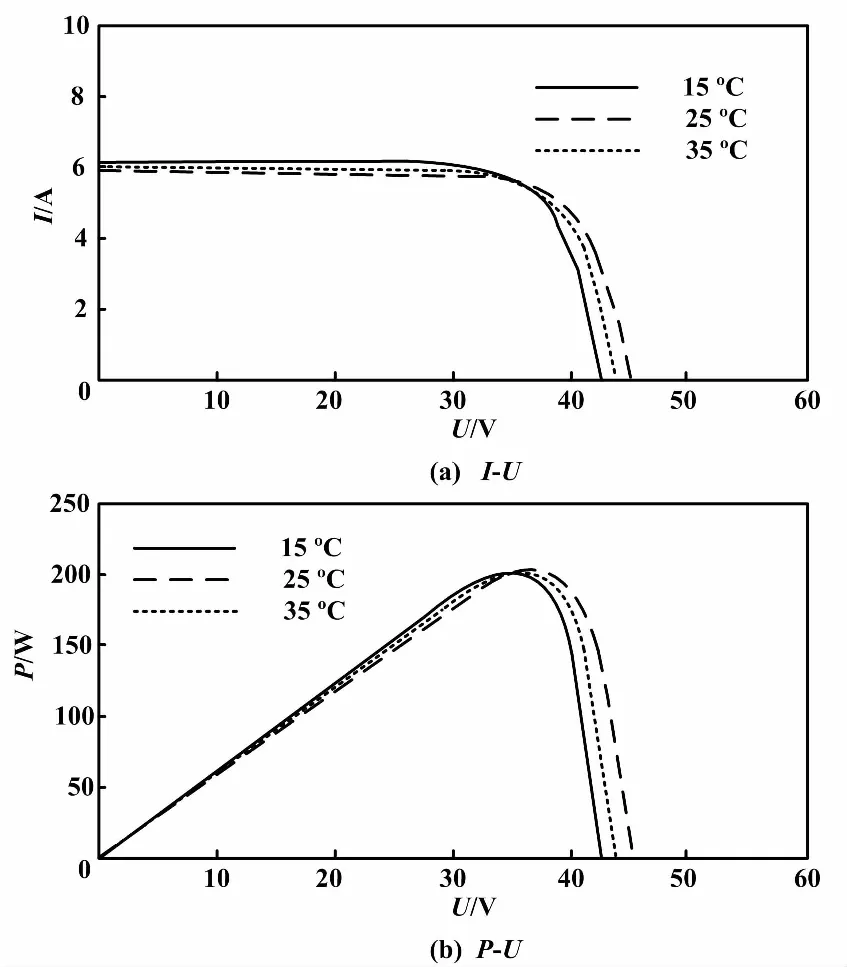
圖6 光伏陣列輸出特性曲線(T等差增加)

從圖6的仿真結果可知：①光伏陣列的Uoc與T成反比，T每升高1 ℃則Uoc約下降2～2.3 mV，Isc與T成正比關系，但T對Isc的影響不明顯；②電池的輸出功率P與T成反比關系，T每升高1 ℃，P損失0.35%～0.45%。

綜上所述，T對電壓影響很大，S對電流影響很大。隨T和S的改變，光伏陣列的輸出特性成非線性關系變化，其最大功率點(maximum power point，MPP)也是隨時變化的。當條件改變時，每條功率特性曲線都有唯一的MPP與之對應。

2.3 光伏發電系統運行特性分析

保持T為25 ℃恒定不變，初設S為1 000 W/m2，在0.5 s時升為1 500 W/m2，0.7 s時降為500 W/m2。利用電導增量法MPPT控制算法，得到的光伏陣列仿真波形如圖7所示。仿真結果表明：當S改變時，光伏陣列輸出電壓基本不變，輸出電流變化較明顯且與S成正比變化，與光伏陣列的輸出特性規律相一致。光伏陣列輸出功率在最大功率處無規律波動，在系統運行時始終工作在最大功率跟蹤狀態，使系統輸出功率最大，有效提高了光伏發電系統的利用率，由此證明了VSG控制策略的有效性。

初始時刻系統帶額定負荷，有功功率5 400 W，無功功率3 200 Var，在0.33 s時有功功率負荷增加940 W，0.5 s時有功功率減少2 270 W，0.667 s后有功功率又增加1 330～5 400 W，整個過程中無功功率保持不變，系統的仿真波形如圖8所示。

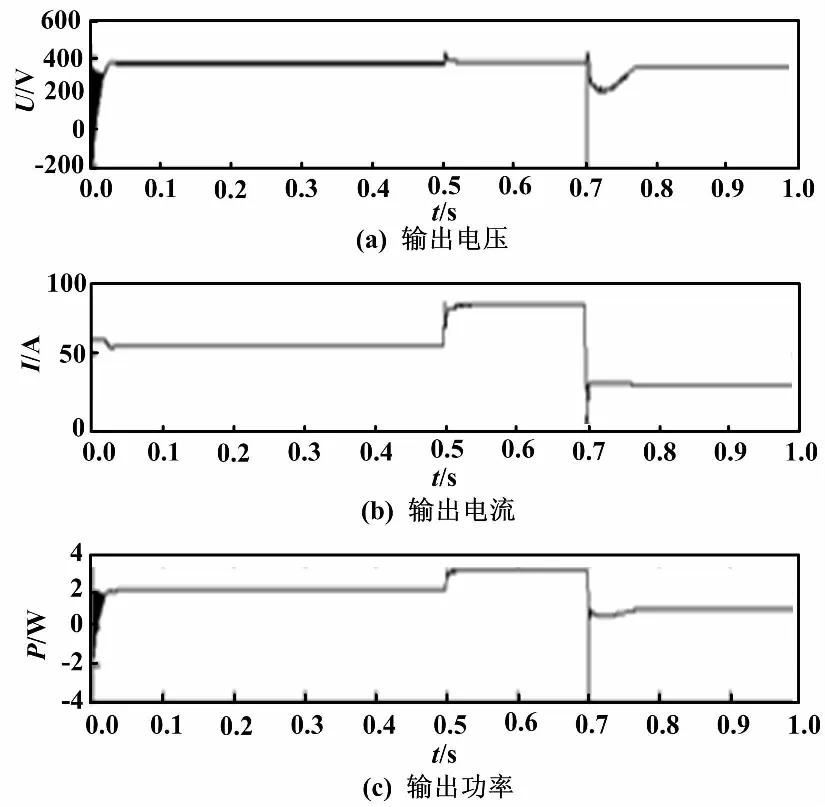
圖7 仿真波形(光照強度變化)

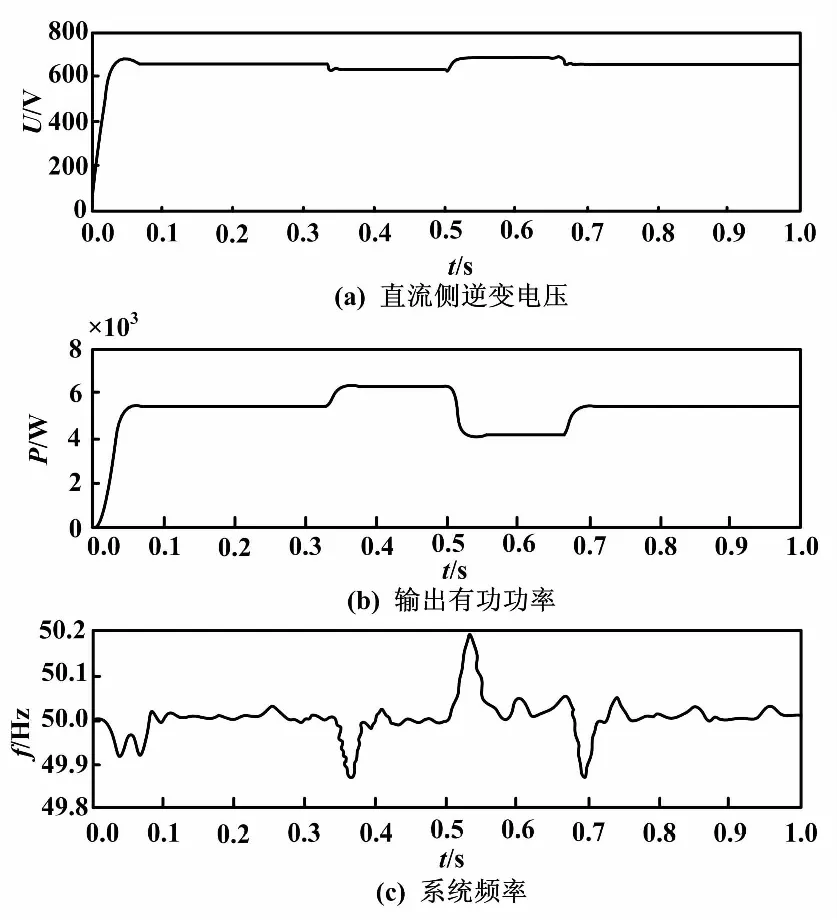
圖8 仿真波形(無功功率保持不變)

從圖8可知，光伏發電系統較容易受到負荷變化等因素干擾，出現運行波動的情況，波動的激烈程度取決于負荷變化大小等多種因素的影響。VSG控制策略能保證直流側逆變電壓和VSG輸出有功功率快速響應負荷變化，維持系統功率平衡，頻率穩定。直流側電壓和系統頻率與負荷成相反趨勢變化，體現VSG控制策略的下垂特性。

3 結束語

VSG具有同步發電機的外特性，對提高電網對光伏陣列發電的消納能力、改善電網變流器接口特性具有重要意義。本文首先介紹了VSG的基本原理，然后建立有功頻率控制和無功電壓控制方法，最后利用MATLAB/Simulink搭建了光伏發電系統的整體仿真模型。試驗驗證了基于VSG的控制策略能根據系統負荷的波動而調整輸出特性，自動維持系統功率平衡，具有很好的調頻功能；同時，其控制結構簡單，同步速度快，實用性強，有效提高了光伏發電系統的輸出效率。

綜上所述，VSG控制在光伏發電系統中極為重要，今后可考慮在VSG故障穿越和VSG并網小干擾穩定控制與暫態穩定控制等方面展開研究。