光學透明膠的超彈性力學性能表征方法研究

賈永臻

(北京大學 深圳研究生院，深圳518055)

柔性顯示屏幕是未來顯示技術的一個重要研發方向. 當前，柔性屏幕各個膜層間常采用光學透明膠材(Optically Clear Adhesive, OCA)進行粘接[1, 2]，柔性屏幕的整體變形過程中，OCA膠材的力學行為最為復雜，易發生粘性流動,導致屏幕表面不平整，是形成波紋狀顯示效果的主要原因. 構建OCA膠材的力學本構模型是仿真分析波紋狀顯示效應的理論基礎. Yeh[3]等率先建立了柔性屏幕的彎折仿真模型，但是該研究將OCA膠材看作簡單的線彈性材料，無法對屏幕攤平及回彈過程中的非線性大變形問題進行解析. 薛宗偉[4]建立了基于小壓縮變形數據的OCA超彈性本構模型，同樣無法應用于柔性顯示屏幕的大變形分析. 基于此，本文展開對OCA膠材力學行為的基礎研究，通過力學性能測試，獲取了OCA膠材在單軸拉伸和簡單剪切兩種大變形模式下的應力應變曲線，并選用唯象模型和熱力學模型，建立OCA膠材的超彈性本構模型.

1 實驗測試

OCA膠材可以在發生大變形的情況下，卸載后自動恢復為初始形狀，符合超彈性材料的一般特征，可以采用超彈性本構模型建立OCA膠材的彈性力學行為. 傳統橡膠類超彈性材料通常采用單軸試驗、雙軸試驗和平面試驗等三種實驗方法獲取其應力應變曲線，但是OCA膠材的模量很低，商業化的雙軸和平面拉伸試驗機的傳感器精度無法準確獲取OCA膠材的應力變化，因此，采用精密度較高的動態機械分析儀和旋轉流變儀，分別對OCA膠材的拉伸行為和簡單剪切行為進行測試.

首先進行試樣制備，將3M公司生產的OCA膠材疊層粘接，厚度h達到1 mm，之后再按照夾具要求完成試樣的切割，兩種變形模式所采用的測試設備及相應的樣品尺寸如表1所示. DMA拉伸測試時，拉伸速率參考ASTM標準D412[5]；采用旋轉流變儀進行簡單剪切測試時，剪切應變速率控制在0.01 s-1.

表1 試驗測試設備及樣品尺寸規格

原始實驗數據經過處理后，可以提取出應力σ和應變ε數據，具體的計算公式如下所示.

(1)單軸拉伸變形模式下，拉伸應變εT和拉伸應力σT的關系式：

(1)

式中，l0表示試樣原始長度；l表示試樣拉伸長度；f表示拉伸載荷.

(2)簡單剪切變形模式下，剪切應變γs和剪切應力σs的關系式如下：

(2)

式中，φ表示平行板的旋轉位移；τ表示平行板扭矩.

2 超彈性本構模型構建及參數擬合

2.1 基本理論

超彈性材料的基本物理特征是彈性變形過程中熵產率為0，不發生能量耗散，因此超彈性材料的本構關系可以通過應變能密度函數U的形式給出：

U=U(l1,l2,l3),

(3)

式中，l1,l2,l3分別為變形張量的三個不變量. 這些不變量和主伸長率λi(i=1,2,3)的關系如下：

(4)

式中，γi表示主應變，I3可以表征材料體積的變化，也用Jei表示，OCA膠材通常認為是不可壓縮的，有I3=1.

將應變能密度函數對主伸長率求偏導，得出Cauchy應力張量與主伸長率的關系[6]：

(5)

式中，p表示靜水壓力.

2.2 應變能密度函數與變形模式

超彈性材料的應變能密度函數主要分為維象模型和統計熱力學模型兩大類，基于經驗的維象模型主要包括Ogden模型、多項式模型、減縮多項式模型、Marlow模型等，其中減縮多項式模型的實驗擬合精度較高，同時仿真計算的收斂性較好，是比較常用的唯象模型之一. 統計熱力學模型則主要有Arruda-Boyce模型、Van der Waals模型和Gent模型等. 下面將分別給出兩類模型中比較有代表性的減縮多項式模型和Arruda-Boyce模型的具體表達式，以及在不同變形模式下推導出的應力應變關系.

由式5可以導出具體變形模式下Cauchy應力張量σi的表達式. 在單軸拉伸變形模式下，拉伸應力的表達式為[7]：

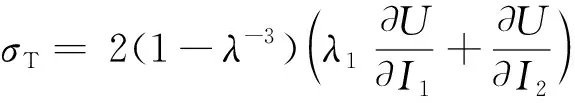
(6)

在簡單剪切變形模式下，剪切應力的表達式為：

(7)

2.2.1 減縮多項式模型

減縮多項式(Reduced Polynomial)模型[8, 9]中忽略了第二變形張量不變量對于應變能的影響，具體的應變能密度函數表達式為：

(8)

式中，N表示多項式的階數；Ci0=(i=1～6)為表征剪切變形的材料常數，Di為表征體積變形的材料常數，對于OCA膠材不予考慮.

將式(8)代入式(6)和(7)，可得到減縮多項式本構模型中的應力-應變關系. 在單軸拉伸變形模式下，其應力應變關系為：

(9)

其中，λT=1+εT在簡單剪切變形模式下，其應力應變關系為：

(10)

2.2.2 Arruda-Boyce模型

Arruda-Boyce模型[10]是一類由非高斯統計理論建立的簡單熱力學模型，其應變能函數表達式如下：

(11)

式中，μ、λm為表征剪切變形的材料常數.

將式(11)代入式(6)和(7)，可得到Arruda-Boyce本構模型中的應力-應變關系. 在單軸拉伸變形模式下，其應力應變關系為：

(12)

在簡單剪切變形模式下，其應力應變關系為：

(13)

3 參數擬合與分析

基于上述推導出的應力-應變關系，結合單軸拉伸和簡單剪切的實驗數據，即可實現超彈性參數的擬合. 目前，尚無商業化的仿真軟件可以將單軸拉伸和簡單剪切數據同時擬合，也未見相關的公式推導和擬合方法等內容有公開報道. 本文利用數學軟件1Stopt，采用Levenberg-Marquardt算法，按照上述本構方程編寫代碼，實現了單軸拉伸與簡單剪切數據的同時擬合，具體結果如表2所示.

表2 OCA膠材的超彈性本構模型參數擬合誤差分析Tab.2 The fitting error analysis of the OCA hyperelastic constitutive model

完成參數擬合的本構模型需進行Drucker穩定性評估，對于通過穩定性評估的本構模型，其應力應變曲線如圖1～4所示.

由應力應變曲線的擬合結果對比后可知，Arruda-Boyce本構模型和一階減縮多項式模型的擬合誤差較大，在拉伸和簡單剪切變形模式下，其力學行為趨近于線彈性. Ritto等[7]進行了基于簡單剪切數據的超彈性本構模型參數擬合，其研究成果指出，擬合誤差控制在0.2以內，就代表了較高的擬合精度. 由表2可知，三階(擬合誤差0.0979)和五階的減縮多項式模型(擬合誤差0.0590)具備了較好的擬合精度，相較而言，五階減縮多項式本構模型的擬合精度更高，但是更高階數的本構模型在仿真分析時會帶來較嚴重的收斂性問題，因此，對于柔性OLED屏幕的應力管控問題，本文推薦采用三階減縮多項式本構模型進行研究.

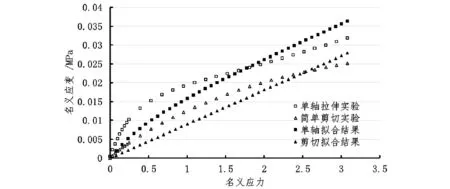
圖1 一階減縮多項式本構模型的擬合結果Fig.1 Fitting result of the first-order reduced polynomial model

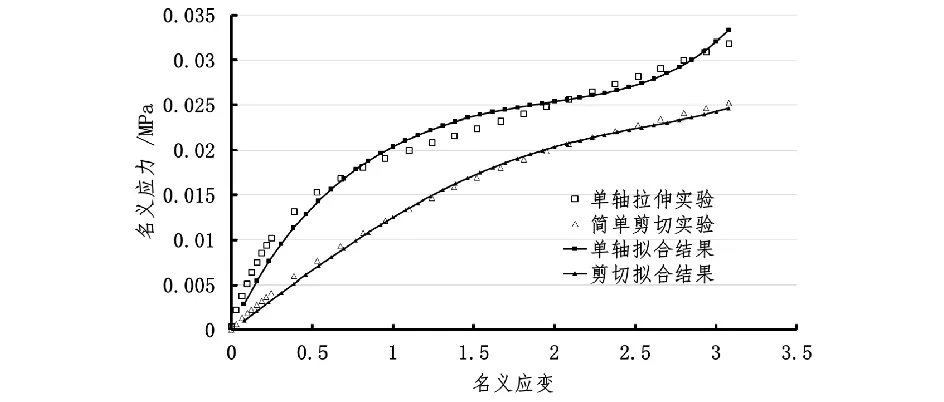
圖2 三階減縮多項式本構模型的擬合結果Fig.2 Fitting result of the third-order reduced polynomial model

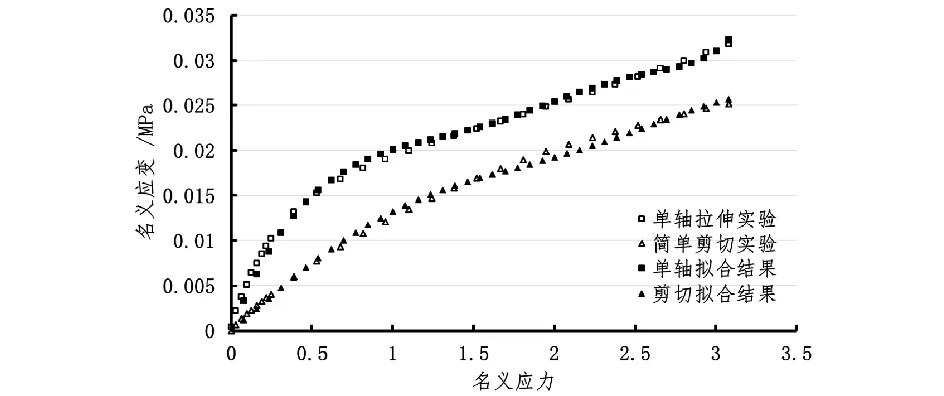
圖3 五階減縮多項式本構模型的擬合結果Fig.3 Fitting result of the fifth-order reduced polynomial mode

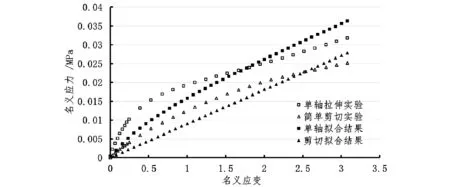
圖4 Arruda-Boyce本構模型的擬合結果Fig.4 Fitting result of the Arruda-Boyce model

4 結語

基于應變能函數的超彈性模型是描述材料超彈性行為的一種有效方法. 本文采用DMA和流變儀準確測得了OCA膠材在拉伸和簡單剪切變形模式下的應力應變曲線，為構建膠材的超彈性模型準備了充足的原始數據. 以減縮多項式模型和Arruda-Boyce模型作為OCA膠材的應變能函數，推導了兩種模型在拉伸和簡單剪切變形模式下的應力應變公式，并使用Levenberg-Marquardt算法，實現了同時運用單軸拉伸與簡單剪切數據，完成本構模型的參數擬合. 通過Druker穩定性評估，最終篩選出了與實驗吻合精度高的本構模型及相應參數. 該理論算法可適用于一般膠黏劑材料的超彈性本構模型構建及參數擬合.