工業純鈦TA2的室溫壓縮蠕變預測模型

，，

(南京工業大學機械與動力工程學院，南京 211816)

0 引 言

鈦及鈦合金因具有耐腐蝕性能好、密度小等優點而被廣泛應用于航空航天、海水淡化、電力和石油化工等行業[1-2]。由于鈦及鈦合金常在高溫下使用，因此在其高溫蠕變性能方面已有較深入的研究[3-6]；此外，工業純鈦TA2的中低溫蠕變行為較為明顯，因此其在拉伸狀態下的中低溫蠕變行為的研究也較多[7]。一般而言，在室溫下當純鈦所受的應力低于60%σs(σs為屈服強度)時，有可能出現蠕變的第一階段；而當應力大于90%σs時，會出現蠕變的第二、第三階段甚至發生失效[8]。馬秋林等[9]對工業純鈦TA2進行了室溫拉伸蠕變試驗，研究了其第一階段的蠕變特性，發現室溫下的拉伸蠕變存在臨界應力。張莉等[10]在150 ℃下對工業純鈦TA2進行了拉伸蠕變試驗，證實了其蠕變的第一階段符合冪律方程，并且在低溫(293～423 K)、低應力(150～350 MPa)條件下，變形主要發生在蠕變第一階段。彭劍等[11]在對工業純鈦TA2進行拉伸蠕變試驗時，發現其在服役溫度(293～423 K)下存在顯著的蠕變現象，并建立了蠕變本構方程，得到了服役溫度范圍內的等效應力-應變曲線。

航空用鈦及鈦合金件大多為受壓結構件，這些結構件一旦產生極小的蠕變應變就會失效[12]，因此研究鈦及鈦合金的壓縮蠕變行為更符合工況要求且更具有理論價值。然而，壓縮蠕變試驗的時間較長，成本較高。若能建立壓縮流變參數和壓縮蠕變參數之間的關系，則可以通過簡單的室溫壓縮試驗來預測室溫蠕變行為。RUSINKO等[13]通過分析TC4鈦合金的壓縮蠕變試驗數據，將蠕變應變速率與蠕變應力聯系起來，采用蠕變曲線對蠕變應變速率進行了預測。SUN等[14]在研究Ti-6Al和Ti-6Al-2Sn-4Zr-2Mo合金的室溫蠕變行為時發現，通過恒應變速率下的流變行為可以預測長時間的蠕變響應，但預測得到的蠕變曲線精度不高。

基于上述研究，作者對工業純鈦TA2進行了恒應變速率室溫壓縮試驗以及恒應力室溫壓縮蠕變試驗，分析了其壓縮流變行為和壓縮蠕變行為；建立了壓縮本構方程參數和蠕變方程參數之間的關系式，利用壓縮蠕變臨界應力進行修正后得到了室溫壓縮蠕變預測模型，并利用試驗數據對該預測模型進行了驗證。

1 試樣制備與試驗方法

試驗材料為由南京寶色股份公司提供的工業純鈦板，牌號為TA2，厚度為10 mm，其顯微組織為α-Ti，化學成分(質量分數/%)為0.044Fe，0.018C，0.019N，0.001H，0.14O，0.4其他元素，余Ti；室溫屈服強度為397 MPa，抗拉強度為481 MPa，伸長率為29.5%。

在工業純鈦板上加工出尺寸為φ6 mm×12 mm的試樣，根據ASTM E139-11，在Instron3367型材料拉伸試驗機上進行壓縮蠕變試驗，壓縮應力保持恒定，分別為200，260，290，350，450，550 MPa，蠕變時間均為80 h，試驗溫度為室溫(23 ℃)，應變速率控制在5×10-5～5×10-4s-1，測得試樣在不同應力水平下的蠕變曲線。根據ASTM E9-09，在Instron3367型材料拉伸試驗機上進行壓縮試驗，應變速率保持恒定，分別為1×10-5，5×10-5，5×10-4s-1，試驗溫度為室溫(23 ℃)，當應變達到10%時結束試驗。

2 試驗結果與討論

2.1 室溫壓縮蠕變行為

由圖1可知：當壓縮應力在260～550 MPa時，試樣的蠕變應變隨應力的增大而增大，隨蠕變時間的延長先快速增大后緩慢增大；當壓縮應力為260，290 MPa時，試樣的蠕變曲線還出現了蠕變應變平臺，該平臺對應的應變即為蠕變飽和應變。由此可見，工業純鈦TA2在室溫下的壓縮蠕變具有很強的應力相關性和時間相關性。當壓縮應力為200 MPa時，試樣的蠕變應變隨蠕變時間的變化不符合蠕變特征，說明試樣未發生蠕變。由此可見，工業純鈦TA2存在蠕變臨界應力。

圖1 試驗和擬合得到試樣在不同壓縮應力下的室溫蠕變曲線Fig.1 Creep curves at room temperature of samples underdifferent compressive stresses by experiment and fitting

在室溫下，試樣的蠕變應變較大(大于2×10-3)，其蠕變應變與蠕變時間的關系可以用冪律方程描述，該冪律方程為

ε=Ata

(1)

式中：ε為蠕變應變；t為蠕變時間；A為材料常數，隨應力和溫度的變化而變化；a為時間指數，代表蠕變過程中的損耗率，a越小，則蠕變過程中的損耗越大。

利用式(1)對圖1中壓縮應力σ在260～550 MPa下的蠕變曲線進行擬合，擬合曲線如圖1所示，擬合結果見表1。

由圖1和表1可以看出，擬合得到的蠕變曲線與試驗得到的較吻合，因此式(1)可以較好地描述試樣在室溫、不同應力水平下的壓縮蠕變曲線。

由于作者研究的是室溫下不同應力水平下的蠕變行為，所以A與σ之間的關系通常可表示為

A=A0σc

式中：A0,c均為常數。

利用式(2)對表1中的A與σ進行擬合，擬合曲線見圖2。由圖2可見，式(2)擬合得到的曲線與數據點存在較大誤差。為了提高擬合精度，用蠕變臨界應力σ0對式(2)進行修正，修正后的公式為

A=A0(σ-σ0)c

(3)

利用式(3)對表1中的A與σ進行擬合，擬合曲線見圖2。由圖2可以看出，式(3)擬合得到的曲線與數據點較為吻合，相關系數達到0.998，擬合公式為

A=0.003 09(σ-252)0.446 51

(4)

由此可知，工業純鈦TA2在室溫下的壓縮蠕變臨界應力為252 MPa。

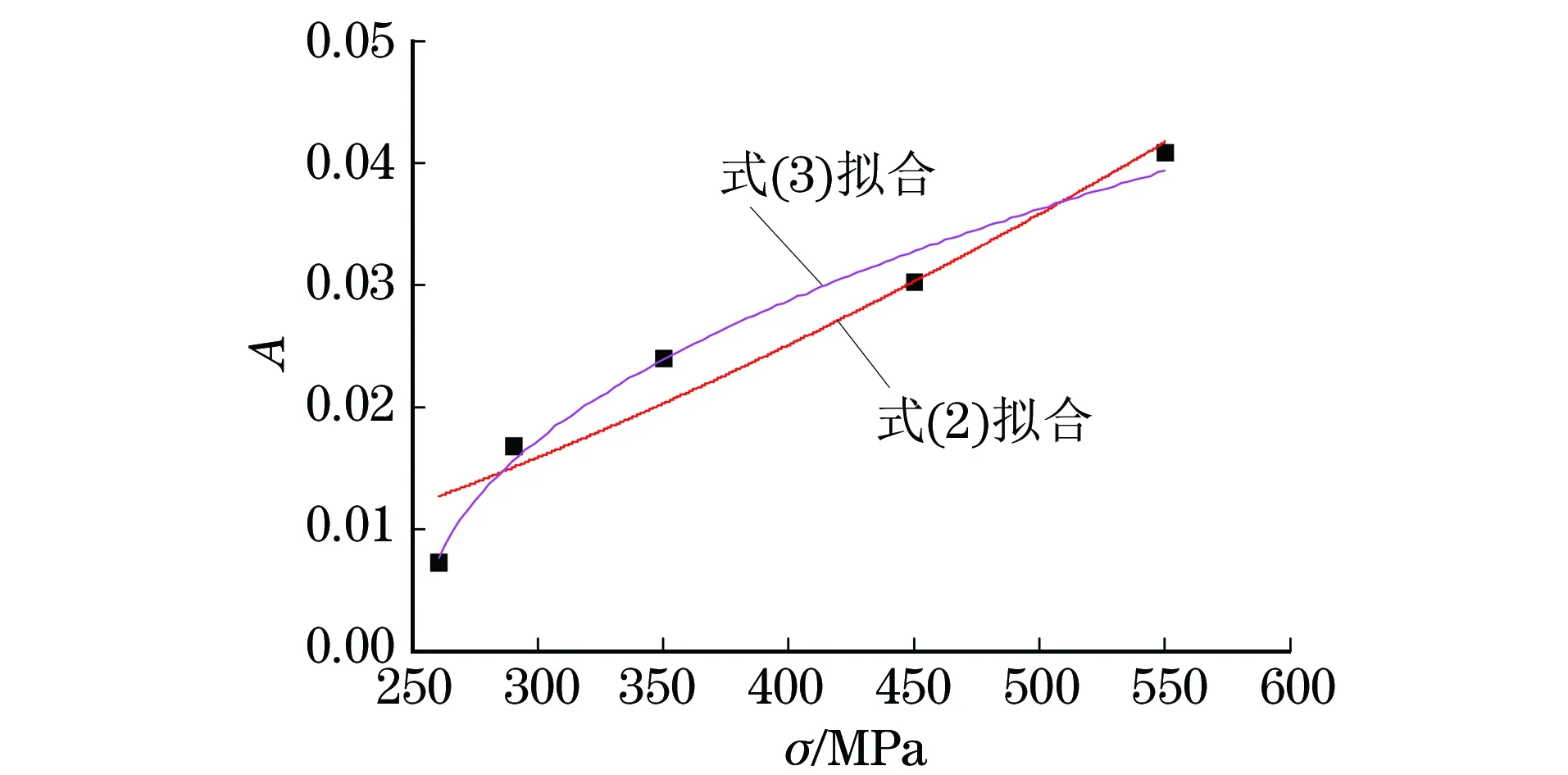
圖2 由式(1)擬合得到的A和σ的關系及其擬合曲線Fig.2 Relationship between A and σ fitted by eq.(1) and theirfitting curves

圖3 在不同應變速率下壓縮時試樣的壓縮應力-應變曲線Fig.3 Compressive stress-strain curves of samples duringcompression at different strain rates

2.2 室溫壓縮流變行為

由圖3可知：在不同應變速率下壓縮時，試樣的壓縮應力增長速率隨著應變的增大而逐漸降低；在相同應變下，壓縮應力隨應變速率的增大而增加。

工業純鈦TA2在恒應變速率下的流變行為可以用Arrhenius方程來描述。考慮到壓縮變形中應變的影響，對Arrhenius方程進行修正，修正后的方程[15]為

σn

(5)

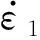
令

K=1/A2

(6)

M=m/n

(7)

N=1/n

(8)

則在室溫下，式(5)可簡化為

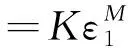
(9)

利用式(9)對試樣的壓縮應力-應變曲線進行擬合，擬合曲線如圖3所示。由圖3可知,在試驗范圍內，式(9)可以較好地描述室溫下工業純鈦的壓縮流變行為，擬合曲線和試驗曲線的相關系數達到0.98。

圖4 在不同應變速率下壓縮時試樣的壓縮應力-應變對數曲線Fig.4 Log compressive stress vs log strain curves of samples duringcompression at different strain rates

將圖3轉換成對數坐標，得到試樣在不同應變速率下室溫壓縮應力-應變的對數曲線。由圖4可見，不同應變速率下的壓縮應力和應變的對數關系近似成線性，且不同應變速率下的壓縮應力-應變對數曲線近似平行，即斜率不變，表明應變速率對該曲線斜率的影響很小。根據文獻[16]，計算得到當應變速率在1×10-5～5×10-5s-1時，N為0.300，當應變速率在5×10-5～5×10-4s-1時，N為0.025。式(9)兩邊取對數，得

(10)

將N的平均值0.16代入式(10)，采用式(10)對圖4中的數據進行一元線性回歸，擬合得到當應變速率分別為1×10-5，5×10-5，5×10-4s-1時，K分別為1 167，1 897，1 999 MPa，M分別為0.72，0.68，0.66，二者的平均值分別為1 688 MPa，0.69。

3 室溫壓縮蠕變預測模型及試驗驗證

為了達到通過壓縮流變行為預測壓縮蠕變行為的目的，需要建立蠕變方程(即冪律方程)中常數A，a和壓縮本構方程(即修正后的Arrhenius方程)中K，M，N之間的關系。

由應變速率的定義，并聯立式(9)可以得到

(11)

對式(11)進行積分可以得到

(12)

假設K與時間無關，則積分后可得

(13)

式(13)和式(1)有著相同的形式，對比兩個方程，可知A，a與M，N，K，σ之間的關系滿足：

a=N/(M+N)

(14)

(15)

由前文可知，試樣的蠕變臨界應力為252 MPa，且A與σ的關系需通過蠕變臨界應力進行修正。因此，利用蠕變臨界應力修正式(15)，得到

(16)

將式(14)和式(16)代入式(1)，得到修正后的蠕變預測模型為

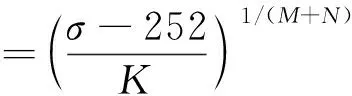
(17)

將K(1 688 MPa)，M(0.69)，N(0.160)代入式(17),即得到工業純鈦TA2的室溫壓縮蠕變預測模型，如下：

(18)

式(14)和式(16)為壓縮本構方程參數與蠕變方程參數的關系式。由式(14)可知，當M趨近于0時，a趨向于1，這時便是穩態流變狀態。因此，修正后的Arrhenius方程可以表征室溫壓縮穩態流變狀態。在室溫下，工業純鈦TA2的蠕變應變積累小于10%，因此在恒應變速率下的壓縮變形和恒應力下的蠕變變形中，應變均應限制在10%以下。

為了驗證室溫壓縮蠕變預測模型的準確性，將壓縮應力代入式(18)，得到試驗條件下工業純鈦TA2的室溫壓縮蠕變預測模型為

(19)

將由式(19)預測得到的蠕變曲線與實測蠕變曲線一起繪制在圖5中。由圖5可見：當蠕變應變較小時，預測曲線與試驗曲線吻合得較好；隨著蠕變時間的延長或蠕變應變的減小，預測值與試驗值的誤差逐漸增大，但是相對誤差均在10%以內。由此可見，式(18)可以較準確地預測工業純鈦TA2的室溫壓縮蠕變行為。

圖5 不同壓縮應力下試樣的蠕變預測曲線與試驗曲線Fig.5 Predicted and experimental creep curves for samples underdifferent compressive stresses

4 結 論

(1) 在室溫壓縮蠕變時，當壓縮應力為200 MPa時，試樣沒有出現蠕變現象；當壓縮應力在260～550 MPa時，試樣表現出明顯的室溫蠕變現象，蠕變應變隨著時間的延長先快速增加后緩慢增加；采用冪律方程擬合蠕變曲線，得到壓縮應力σ和材料常數A的關系式，用蠕變臨界應力對A-σ關系式進行修正后，擬合得到試樣的室溫蠕變臨界應力為252 MPa。

(2) 利用壓縮流變應變對Arrhenius方程進行修正，修正后的Arrhenius方程可以很好地描述試樣的室溫壓縮流變行為。

(3) 建立了室溫壓縮蠕變方程參數和壓縮本構方程參數的關系式，利用蠕變臨界應力進行修正后，得到基于室溫壓縮試驗數據的室溫壓縮蠕變預測模型，采用此模型計算得到的室溫壓縮蠕變預測曲線與試驗曲線的相對誤差均在10%以內。