無控火箭彈彈道失穩機理研究

樊會濤,楊林沖

(中國空空導彈研究院,河南 洛陽471009)

在空空導彈研制中,無控火箭彈是一種過渡狀態,用于評估火箭發動機在飛行條件下的穩定性、安全性,并初步了解導彈的氣動特性、彈架分離安全等情況。出于載機安全考慮,在有控彈空中發射試驗之前通常安排若干數量的火箭彈進行地面/空中發射,歷史上曾經出現過火箭彈彈道明顯擺動的現象。

為適應現代戰爭對速度、射程、機動性及內埋掛裝等要求,先進空空導彈相對于上一代產品,彈身更修長,表面更整潔,氣動面更窄小[1]。先進空空導彈火箭彈彈道不平穩的現象非常明顯,地面發射稍好,空中發射情況尤其惡劣,去掉導彈前翼面后,反而出現了更壞的情況。

按照傳統的飛行力學理解,無控火箭彈在一定條件下出現擺動是彈體動力學中的固有現象,但由于無控火箭彈本身是靜穩定的,因此彈體的擺動也不會持續地增大[2-3],更不應當發散。然而在先進空空導彈研制中卻出現了彈道發散的現象,甚至直接引起導彈解體的飛行故障。以前工程實踐中抑制火箭彈擺動的技術措施也失去了作用。

文獻中對于火箭彈的彈道穩定性問題有很多不同程度的分析研究,但研究對象主要集中在兵器領域的無控火箭彈,其本身作為最終交付產品并且地面發射。對于空空導彈的無控火箭彈,它首先不是最終交付產品,僅僅是產品研制中的一種過渡狀態;其次,空空導彈作為打擊空中機動目標的精確制導武器,它的氣動外形、發射方式與兵器領域的無控火箭彈有著本質的差別。因此,有必要對先進空空導彈火箭彈出現彈道失穩現象、導致飛行故障的物理機理,需要采取的技術措施開展深入研究。

1 無控火箭彈動力學模型

為研究火箭彈彈道失穩的機理,建立如下無控火箭彈動力學模型[4]。

1.1 火箭彈彈體縱向運動的線性化模型

按照經典的飛行力學理論,彈體縱向姿態運動方程可簡化為

(1)

式中:?為彈體俯仰角,θ為彈道傾角,α為攻角,δ為縱向通道舵偏角,a1為阻尼系數,a2為靜穩定系數,a3為舵效率系數,a4為法向力系數,a5為舵升力系數。

據此,縱向運動(俯仰/偏航)舵偏角到攻角之間的傳遞函數為

(2)

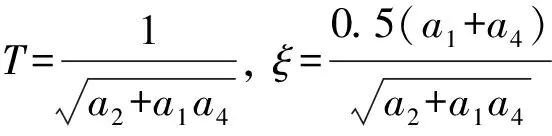
由于a1a4+a2?a5,因此τ≈0。式(2)可簡化為

(3)

1.2 彈體的橫向(滾轉)運動的線性化模型

彈體的滾轉運動方程可簡化為

(4)

式中:c1為橫滾阻尼系數,c3為橫滾舵效率系數,γ為導彈橫滾角。

橫滾舵偏角δx到滾轉角速度ωx之間的傳遞函數為

(5)

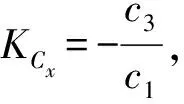
1.3 縱向運動與橫向運動之間交叉耦合的導彈空間運動方程系

為了更好地分析火箭彈擺動的原因,列出考慮了縱向運動與橫向運動之間交叉耦合的導彈空間運動方程系為

(6)

式中:a1～a5為前文已述及的彈體縱向運動動力學系數;ωz,ωy和ωx分別為彈體俯仰、偏航和橫滾角速度,ωz和ωy是前文ωn具體的兩項;αI,αII和δI,δII分別為2個縱向通道(俯仰/偏航)的通道攻角和通道舵偏角,δIII為橫滾通道舵偏角(同前文中的δx)。ΔMIII(δIII)為橫滾通道驅動力矩項,它反映的是三通道舵偏(通常是安裝誤差)引起的橫滾力矩;Mxk0(αI,αII,δI,δII)為斜吹力矩項,它反映的是縱向運動對橫向運動的影響。ωxωy和ωxωz為陀螺效應項,ωxαII和ωxαI為慣性項,它們代表的是橫向運動對縱向運動的影響。

2 火箭彈彈道失穩機理分析

本節利用前面建立的火箭彈動力學模型對火箭彈彈道失穩機理進行數字仿真研究。

2.1 無控火箭彈飛行彈道上的壓心、質心變化特性

導彈的相對靜穩定度用質心與壓心之間的距離占全彈長度的百分數(η)來表示。空空導彈的燃料布置于后彈體,主動段質心持續前移,一般理解其靜穩定度在主動段應持續增加。但實際上還必須考慮全彈氣動壓心的變化:主動段導彈速度劇烈增加,壓心快速前移,從這個角度來講靜穩定度又是在減小的。導彈靜穩定度受質心、壓心二者變化的綜合影響,是它們“賽跑”的結果。這樣在分析火箭彈的靜穩定度時,就不能僅僅分析初始狀態的質心、壓心相對位置,而要進行全彈道的動態分析。圖1是某火箭彈飛行彈道上的相對靜穩定度變化曲線,注意到在主動段(前13 s)其相對靜穩定度是先增加后降低再增加的。

2.2 火箭彈彈道共振現象的必要條件

通過質點彈道數字仿真,可得空中發射火箭彈在整個飛行過程中縱向運動頻率ωy(t)的變化曲線和橫向運動(橫滾)頻率ωx(t)曲線,如圖2所示。ωy(t)在發射條件(高度、速度和仰角)確定后就被唯一確定了;ωx(t)的高低則是不固定的,它不但受發射條件的影響,還要由具體的等效安裝誤差(將所有的橫向不對稱因素都等效進去)來決定,ΔδIII增加,ωx的曲線抬高,反之下降。

在圖2中彈體縱向運動頻率與橫向運動頻率(滾動轉速)有兩處相等,在這兩個點上具備了傳統意義上的彈道共振的必要條件。具體到每一枚火箭彈,由于ΔδIII的不確定性,彈道上會不會出現頻率相等的點(或相近的區域)、何時出現都具有很大的不確定性。并且在頻率相等的點上(或相近區域)彈道僅僅是短時間的共振還是維持長時間持續共振同樣也是不確定的。短時間的彈道共振一般不會引起導彈過載的持續增加且會自行消失,危害不大,而長時間共振就可能引起彈體過載的持續增加,甚至引起故障。

彈道明顯擺動(共振)的發生需要同時具備2個必要條件:縱橫向運動頻率相近、縱向通道存在一個不可“忽略”的等效舵偏δI/δII(舵面安裝誤差、彈體的軸線不對稱、彈體的彈性變形和發動機推力偏心等因素都可引起),由它激勵出一定量值大小的攻角,引起彈道擺動。縱橫向頻率相近的前提是客觀上存在一個不可“忽略”的等效ΔδIII,它“驅動”火箭彈的自轉轉速達到縱向運動頻率附近。

2.3 火箭彈彈道持續共振現象的內在機理——似月運動和轉速閉鎖

從前面的數字仿真結果注意到,空空火箭彈在全彈道上縱向運動與橫向運動頻率相同的點只有2個并且很快便錯開了,但實際的飛行試驗中卻出現持續的共振擺動,有必要對此進行分析。

空空導彈采用軸對稱氣動外形,相對滾轉角Φ的定義見圖3,在攻角存在的情況下,它直接決定氣流吹到導彈的方位。導彈的誘導滾轉力矩Mxs與攻角α的大小正相關。攻角一定時,誘導滾轉力矩Mxs是相對滾轉Φ的正弦函數,四分之一圓周上Mxs與Φ關系曲線見圖4所示,圓周的其余部分呈周期變化。

考慮了誘導滾轉力矩Mxs后,火箭彈的滾轉方程(4)可寫為[2-5]

(7)

式中:kxw為導轉力矩系數,kxz為滾轉阻尼力矩系數,kxs為誘導力矩系數。

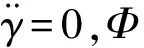
如果似月運動長時間的持續下去而不被打破,火箭彈轉速將一直被鎖定在共振轉速附近,稱為“轉速閉鎖”。“轉速閉鎖”會導致攻角急劇增大,形成長時間阻力增大和彈道發散,出現“災變性偏航”,導致近彈和掉彈[5]。過大的攻角甚至使得導彈橫向力超過設計極限而造成火箭彈空中解體。

2.4 對火箭彈飛行故障的數字仿真研究

針對先進空空導彈火箭彈空中發射試驗飛行故障,利用前文動力學模型開展數字仿真研究。該次試驗情況如下:火箭彈不帶前彈翼,載機平飛,發射海拔高度8 600 m,飛行馬赫數為0.9。發動機點火后,機彈分離正常。初始段彈體有小幅擺動,并很快減弱。4.5 s時前彈道平直,發動機尾焰穩定。4.7 s時彈體明顯開始旋轉擺動,起初幅度較小,5.6 s時幅度增大,接著擺動加劇,到7.7 s時發動機解體。共進行8次擺動,頻率約2.0～2.6 Hz,呈逐漸增大趨勢,最大擺動幅度達28°,如圖6所示。7.3 s時發動機尾部出現明顯的高亮度火團,持續0.4 s到7.7 s發動機出現一團火光,空中解體,火箭彈前彈體向前繼續飛行一段后掉落。

由于在發射前沒有進行測量,只能假設一組工程上可能的氣動面安裝誤差(δI=Δ1,δII=Δ2,δIII=Δ3)、發動機推力偏心數值(ε=Δ4)進行數字仿真來復現故障[6]。圖7為該次空中發射火箭彈縱向運動頻率和橫向運動頻率曲線。注意到,從4.4 s開始一直到7.7 s火箭彈的縱向運動頻率和橫向運動頻率一直非常接近,為彈道共振創造了必要的條件。圖8為地理坐標系下觀察到的攻角曲線,由于導彈是滾轉的,它呈現出交變的特征。圖9是彈體系下火箭彈的過載變化曲線,火箭彈的過載持續增大而超過設計范圍,加之在彈體周向上方位保持不變,最終導致發動機在這個非工況過載環境下工作而燒穿殼體,引起空中解體的飛行故障[7]。

2.5 無控火箭彈飛行彈道穩定性影響因素

本節按照前文故障復現所采用的數學模型和發射條件進行數字仿真研究,探討不同的初始輸入條件對無控火箭彈飛行彈道穩定性的影響情況。

①輸入條件1。

舵偏角安裝誤差:δI=Δ1,δII=Δ2,δIII=Δ3;

發動機推力偏心:ε=Δ4;

該組輸入條件是2.4節中故障復現所采用的,計算結果作為對比研究的基準。

②輸入條件2。

舵偏角安裝誤差:δI=0.5Δ1,δII=0.5Δ2,δIII=Δ3;

發動機推力偏心:ε=Δ4;

該組輸入條件相對于條件1,縱向通道等效舵偏誤差角降低一倍。仿真結果顯示火箭彈的縱向運動頻率和橫向運動頻率曲線與圖7相同,攻角曲線和過載曲線相對于圖8、圖9相應地降低了一倍左右。

③輸入條件3。

舵偏角安裝誤差:δI=Δ1,δII=Δ2,δIII=0.5Δ3;

發動機推力偏心:ε=Δ4;

該組輸入條件相對于條件1,橫向通道等效舵偏誤差角降低一倍。計算結果見圖10和圖11。注意到,圖10中的縱向運動頻率、橫向運動頻率相差較大,保持在7 rad/s以上,不具備彈道共振的必要條件,圖11的攻角很小。

④輸入條件4。

舵偏角安裝誤差:δI=Δ1,δII=Δ2,δIII=Δ3;

發動機推力偏心:ε=Δ4;

該組輸入條件與條件1相同,是故障復現采用的條件。但火箭彈的質心通過配置前移后,保證整個飛行彈道導彈的靜穩定度在10%以上。仿真結果顯示,火箭彈的縱向運動頻率和橫向運動頻率相差較大,保持在6.5 rad/s以上,類似于圖10已經不具備彈道共振的必要條件,激發的攻角很小。

先進空空導彈為適應現代戰爭對速度、射程和內埋掛裝的新要求,橫向尺寸、氣動面面積被大幅度壓縮,唯有大幅降低導彈的靜穩定度才能滿足機動性(操縱性)要求。去掉前翼后,導彈橫向阻尼系數被明顯降低,在其他條件不變的情況下,導彈的橫滾頻率上升得更快,更容易到達縱向頻率附近,發生持續彈道共振的可能性大幅提高。相對于地面發射,火箭彈空中發射時整個主動段的飛行速度更高,壓心前移的現象更加突出,火箭彈橫滾頻率上升得更快,更容易到達縱向頻率附近。這就解釋了為何先進空空導彈更容易出現彈道失穩,空中發射情況更糟糕,去掉前翼的傳統措施為何“事與愿違”。

3 保證無控火箭彈飛行穩定的措施

通過前面的數字仿真研究并結合工程實踐,為避免火箭彈飛行彈道的不穩定現象,提出如下的技術措施:被動措施和主動措施。被動措施就是除了保證彈體各艙段的連接精度,舵面、翼面和電纜整流罩等的安裝精度、對稱度以外,對每一片舵面、翼面的零位偏差要控制在0.2°之內,所有舵面零位偏差的代數和小于0.3°,翼面的也要小于0.3°,且避免上述2個代數和同號;保證舵面、翼面的剛度和強度滿足要求;按指標要求嚴格控制發動機的推力偏心。主動措施就是嚴格控制火箭彈的質心位置,必要時通過配重將其向前調整,將全彈道的靜穩定度控制在10%以上。無控火箭彈作為空空導彈工程研制中的過渡狀態不需交付用戶,對氣動面的選配安裝、質心位置的適度調整是可行且有意義的。

被動措施、主動措施的本質都是降低或避免縱橫向通道之間的相互耦合。前者通過大幅減小導彈的橫滾頻率使得ωx遠小于縱向固有頻率ωy,相當于盡力壓低圖2中ωx(t)曲線的高度,使其在整個彈道上都處在ωy(t)的下面,且保證一定安全距離。后者通過增加縱向固有頻率ωy,相當于盡力抬高圖3中的ωy(t)曲線的高度。另一方面被動措施通過降低等效的縱向通道舵偏面偏差,來降低激勵輸入(即干擾攻角)。主動措施通過提高導彈靜穩定度,使得單位舵偏引起的干擾攻角明顯減小,直接抑制了彈道的擺動幅度,相對于被動措施效果更直接、更明顯。

必須克服火箭彈結構簡單、技術含量不高的麻痹思想。由于缺少飛行控制系統,沒有引入人工增穩裝置,火箭彈的彈道穩定性全靠自身的靜穩定度儲備來保證。為避免人為地引入干擾,對外形的幾何對稱性要求更高,對火箭彈的加工、安裝精度的控制必須從嚴。先進空空導彈火箭彈綜合采用被動措施、主動措施后的數字仿真結果顯示火箭彈飛行彈道平穩,且已通過飛行試驗驗證。

4 結束語

本文揭示了空空導彈火箭彈彈道失穩的機理,對型號研制中出現的彈道失穩問題進行了研究。先進空空導彈采用放寬靜穩定度外形設計,使得無控火箭彈縱橫向運動耦合共振變得更加容易、頻繁,共振的強度更加劇烈。

避免火箭彈縱橫向運動耦合共振發生的技術措施分為被動措施和主動措施,被動措施通過限制以舵翼面安裝誤差為代表的各類工程誤差,來抑制火箭彈滾轉的角速度、干擾激勵輸入,消除彈道共振現象發生的外因。主動措施通過前移火箭彈的質心來增加其靜穩定度,進而提高其縱向運動的抗干擾能力,同時也增加了火箭彈的縱向運動固有頻率,消除彈道共振現象發生的內因。

縱橫向運動耦合共振問題是無控火箭彈所特有的。最終交付用戶的空空導彈都是帶有控制系統的,其橫滾角被控制在零值附近很小的一個范圍內,并且正反2個方向來回波動,不會出現上述問題[8]。