不同橢球與投影參數的兩套高斯平面坐標的變換方法

歐海平,呂長廣,喻永平,劉顯濤

(1.廣州市城市規劃勘測設計研究院，廣東 廣州 510060;2.山東正元建設工程有限責任公司，山東 濟南 250100；3.黑龍江第二測繪工程院，黑龍江 哈爾濱 150025)

2018-07-01起，我國開始啟用CGCS2000坐標系，根據廣州市的具體情況，考慮原有廣州坐標海量數據資料有效利用原則，廣州市建立了以CGCS2000橢球為支撐的廣州2000坐標系。廣州2000坐標系建立過程中，需要考慮不同坐標系的橢球參數和投影參數，需要分析這些因素對坐標變換關系的影響，建立基于不同參考橢球參數的坐標系轉換方法，指導各種坐標系轉換及廣州2000坐標系的建立。

1 不同橢球和投影參數對高斯投影坐標的影響分析

參考橢球形狀和大小的差異體現在長半徑a和扁率f的不同，高斯投影參數主要是中央子午線L0、投影面高程和投影坐標偏差常數(X0，Y0)。若采用北方向夾角α、尺度比m和平移常數(x0，y0)4個參數進行兩個不同參考橢球的高斯投影坐標轉換，其轉換模型比較簡單，但要求兩種坐標是線性關系。如果兩高斯平面坐標之間的關系是非線性的，直接采用四參數模型進行坐標轉換精度很差，而精準轉換則其轉換模型比較復雜。因此，在分析不同橢球和幾何參數對高斯投影坐標的影響基礎上，提出削弱非線性影響因素，建立精準且簡單的坐標轉換模型和流程。

高斯投影坐標的正算公式為:

(1)

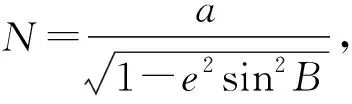
(2)

(3)

投影的長度比：

(4)

根據式(1)～式(3)，不難發現當橢球半徑為a，增大δa時，投影坐標變為：

(5)

這說明橢球長半徑變化對高斯投影坐標的影響是線性的。盡管橢球扁率對投影坐標的影響是非線性的，但不同橢球的扁率相差甚小，其非線性部分的影響可忽略不計。順便指出，兩個坐標系定向參數的影響也相差甚小，可以忽略不計。其定位參數不同或投影面高程不同時，其影響特性也是線性的，因為可以通過膨脹橢球長半徑a，使兩個橢球面在區域范圍內一致，因此其影響與式(5)相同，只要將式中的δa改為兩者的投影面高程之差。

在式(3)中投影點的子午線收斂角是非線性變化的，如果兩個點的經線分別為L和L+ ΔL(ΔL為經差)，則略去最后一項后由式(3)可得兩者的收斂角之差為

ΔL(3l2+3l·ΔL+ΔL2)(1+3η2+2η4)+….

(6)

顯然，兩者的子午線收斂角差值隨ΔL增大而變大，只有當ΔL很小時，才能忽略其影響，采用一個旋轉參數α來實現兩個高斯投影坐標系的轉換。

同樣將式(1)第二式的首項y=NcosBl代入式(4)，當兩個點的經線相差ΔL時，由式(4)得兩者的尺度比之差為

(7)

顯然，尺度比之差也隨ΔL增大而變大，當ΔL很小時，才能忽略其影響，才能用一個尺度比參數來進行兩個高斯投影坐標系的轉換。

上述討論的結果，對于同一點，在兩個中央子午線(L0及L0+ΔL)的高斯投影情況同樣成立。

2 不同橢球和投影參數的高斯投影坐標的變換方法

在兩平面坐標系的四參數模型中，其參數為北方向夾角α、長度尺度比m和平移常數(x0，y0)，通過兩個坐標系的公共點坐標成果計算轉換參數，按式(8)進行坐標轉換。

(8)

式中：x0，y0為平移參數；α為旋轉參數；m為長度尺度比參數。

坐標轉換的真諦在于使α=0、m=1時，通過加適當的平移常數使兩坐標值達到一致。

高斯投影坐標系參數除投影的參考橢球體外，還有投影的中央子午線、投影面高度和加常數，中央子午線與投影后的坐標系的北方向密切相關，投影的高程面高低則與坐標系的尺度比密切相關。

對于經差ΔL較大的不同中央子午線的高斯投影坐標系，直接采用四參數模型進行坐標轉換，由于子午線收斂角及高斯投影長度投影變形的特性，很難得出較為滿意的坐標轉換精度。

根據對不同橢球和投影參數對高斯投影坐標的影響分析結論，對于不同參考橢球體(如克拉索夫斯基橢球體、CGCS2000橢球)的高斯投影坐標，當投影的中央子午線經差ΔL較小時，子午線收斂角差值和尺度比差值較小，可以忽略其影響，能用一個尺度比參數和一個旋轉參數來表示兩個高斯投影坐標系的轉換關系，此時采用四參數模型進行坐標轉換，可得出較為滿意的坐標轉換精度，這在廣州坐標與廣州2000坐標的轉換及廣州2000坐標系建立中得到較好的應用。

3 應用實踐

3.1 廣州坐標與2000國家大地坐標的轉換實踐

在廣州市城市規劃和建設中一直使用廣州坐標系， 60多年來，積累了海量的廣州坐標系數據資料，廣州坐標系是基于北京54參考橢球的高斯正形投影的獨立坐標系，投影中央子午線為廣州白云山摩星嶺所在經線(E113°17′)，投影面為廣州平均高程。

廣州坐標轉換到2000國家大地坐標系的投影坐標(CGCS2000橢球、38°帶(E114°))，直接采用四參數模型進行坐標轉換，其轉換精度很差(1 m左右)。若先將廣州坐標進行換帶計算處理，轉換到中央子午線(E114°)的投影坐標，由于兩坐標系投影的中央子午線經差ΔL=0，此時再采用四參數模型對換帶投影后的坐標和2000國家大地坐標進行轉換，可得出較為滿意的坐標轉換精度。

流程：廣州坐標(X1，Y1，E113°17′、克拉索夫斯基橢球體)→高斯坐標反算(B，L)→高斯坐標正算(X2，Y2，E114°、克拉索夫斯基橢球體)→四參數模型轉換→2000國家大地投影坐標(X3，Y3，E114°、CGCS2000橢球)。

按上述流程方法，以156個高等級控制點坐標求出四參數模型參數編制轉換程序，對另外的98個高等級控制點進行轉換檢核，轉換精度較好，見表1。

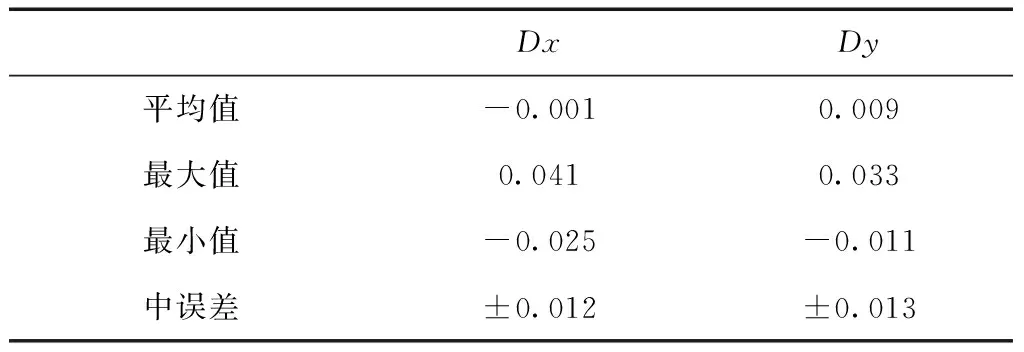
表1 轉換精度統計表 m

3.2 廣州2000坐標系建立應用

不同橢球和投影參數的高斯投影坐標的變換方法及原理，在廣州2000坐標系建立中得到較好應用。廣州市區域的經度范圍是E112°57′～ 114°03′，使用2000國家大地坐標系標準投影帶高斯坐標(3°帶投影第38°帶投影坐標)，有超過1/2的廣州市區域處于長度投影變形超過1/40 000范圍，為此，需要建立2000國家大地坐標系的城市獨立坐標系，即廣州2000坐標系。

綜上分析，對于不同參考橢球體的高斯投影坐標，當投影的中央子午線經差ΔL較小時，采用四參數模型進行兩個坐標轉換，坐標轉換精度較好。根據坐標轉換的逆過程，在廣州2000坐標與廣州坐標一致的前提下確定廣州2000坐標系參數(中央經線L0、投影面高程H和坐標加常數(X0，Y0))，此時兩坐標系北方向夾角α=0、長度尺度比m=1，建立流程如圖1所示。

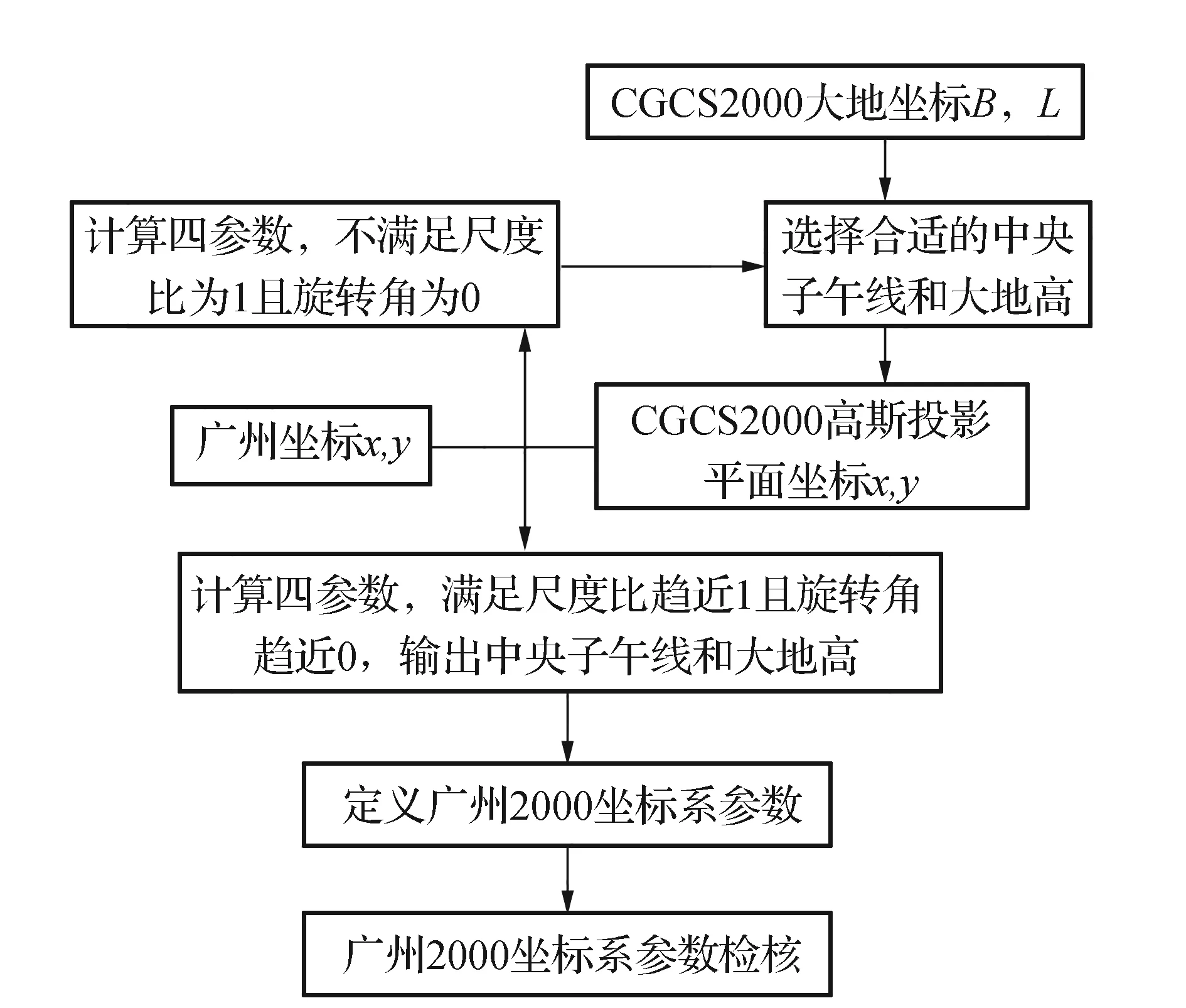
圖1 廣州2000坐標系建立流程

在廣州市坐標系整合統一中，已確定了廣州市似大地水準面精化高精度控制網(156點)和廣州市GPS首級(二等)平面測量控制網(98點)的CGCS2000大地坐標以及廣州坐標。按照廣州2000坐標系的建立原則，在廣州坐標值和廣州2000坐標值相等的條件下(旋轉角α=0、尺度比m=1、+X0、+Y0)，通過156個控制點坐標值反演求出廣州2000坐標系參數：投影中央子午線L=113°17′**″(與廣州坐標系中央子午線的經差約數s)、投影面大地高H=-10.** m、平移參數為X0=-252 9615.*** m,Y0=41 123. **** m。

根據此參數，對控制點的CGCS2000大地坐標在2000橢球體上進行高斯投影計算，得到廣州2000坐標。

156個格網點廣州2000坐標與廣州坐標差異比較(內符合精度)如表2所示。

表2 內符合精度統計表 m

98個格網點廣州2000坐標與廣州坐標差異比較(內符合精度)如表3所示。

表3 內符合精度統計表 m

根據上述方法確定的廣州2000坐標系，其坐標值在廣州行政區域范圍內與廣州坐標較差均在0.05 m以內，在±0.05 m精度下，廣州2000坐標與廣州坐標可等同使用。

4 結束語

本文分析了不同橢球和投影參數對高斯投影坐標的影響，對不同參考橢球的高斯投影坐標精準銜接技術進行探討，提出了不同橢球和投影參數的高斯投影坐標的轉換方法，并運用于多個歷史時期空間數據轉換和廣州2000坐標系的建立實踐中，具有極高使用價值。本文成果應用過程中，得到了以下結論：

1)對于基于不同參考橢球體(如克拉索夫斯基橢球體、2000國家參數橢球體)的高斯投影平面坐標，在投影的中央子午線偏差不大的前提下，通過四參數模型進行坐標轉換，可得到較好的轉換精度。

2)通過適當的投影面投影調整可使尺度因子m=1、通過適當微調投影子午線可以旋轉角α=0，再通過加適當的平移參數可使在不同參考橢球體高斯投影的兩套坐標值達到一致。就廣州2000坐標系建立的實踐情況來看，建立的廣州2000坐標系與廣州坐標系符合性較好，這對新建坐標系統坐標與舊有坐標系坐標精準銜接，促進CGCS2000大地坐標系在大城市中應用有較好的示范作用。