線性參照系與大地坐標系的相互轉換

鄧興升， 黃小鵬

(長沙理工大學 交通學院, 長沙 410114)

在道路交通領域，位置信息不是由單一的坐標確定，而是根據實際需求配合線性參照系統(Linear Referencing System, LRS)共同確定[1]。由于道路的線性特征，采用線性參照系統更有優勢，符合人們對道路要素描述的習慣和理解能力。用大地坐標來描述道路特征點的位置，往往沒有用里程數更直接、更易理解；線性參照系統也是為了解決交通網絡中事件定位和表達而設計的。目前高速公路普遍采用里程樁進行線性定位[2]，以距離替代坐標來定位空間事物或事件。交通運輸地理信息系統GIS-T(Geographic Information System for Transportation)的定位采用線性參照系統[3]，是與常規GIS的區別之一；面向對象的公路網絡及立交模型均是基于線性參照系統[4]。單純二維坐標參考系統并不適合大型公路地理信息系統建設[5]，現有GIS-T模型一般同時采用兩種空間位置參照系，即一維線性參照系和二維空間參照系[6]。線性參照系的顯著特點是可以采用線性分段技術在GIS中完成空間相對位移定位[7]。

衛星定位技術常用于獲取道路特征點的三維大地坐標，但表達交通信息時常用線性參照方法LRM(Linear Reference Method)和線性參照系，而不采用空間參照方法。線性參照方法是在一個定義好的交通網絡中由已知位置和路徑，在LRS空間通過與已知參照點間的偏移距離，來確定未知位置的度量方法。基于一維線性系建立空間數據模型，能夠將一維線性坐標轉換為實際地理空間坐標[8]。根據需要可將路段進行動態分段，并將屬性沿程變化存儲為獨立事件屬性表，使一維線性參照系為基礎建立的各類屬性集能與二維參照系為基礎建立的空間位置相關聯[9]。實現線性參照系與大地坐標系之間的融合和高效轉換是一項重要的基礎工作，本文采用模型直接計算兩坐標系的轉換參數，給出道路彎曲度近似度量的兩個指標，及兩坐標系之間相互轉換的方法，其中大地坐標對球面經緯度和空間直角坐標兩種形式均適用，并列舉實例進行分析驗證。

1 線性參照系與大地坐標系相互轉換

1.1 線性參照系統的建立

線性參照系統最早由Baker和Blessing在1974年提出，通常由交通網絡、線性參照方法和參照基準控制3部分組成。實際道路網形狀復雜，基線網僅是一個抽象的近似映射，提供不同線性參照方法間的定位參照及相互轉換基準[10]。基線網中特征點線集合，由錨固點(Anchor Points)及錨固段(Anchor Sections)組成。錨固點即道路特征點，具有明顯地物特征、且位置不易改變，如道路起終點、主要道路交叉口、大中型橋梁中點、特征里程樁點等。錨固段即路段，由兩個有序的錨固點組成。錨固點的定位包括平面坐標及線性參照距離，參照點即某錨固段的里程零點，是線性參照系的原點。參照點可采用具有重要地理位置的錨固點，由于線性參照系統采用動態分段機制，在一個基線網中，任何一個錨固點根據需要都可能作為參照點。

1.2 道路彎曲度計算與線性插值

由于線性插值是將錨固段近似視為直線處理的，因此需對道路彎曲度進行度量。道路彎曲度評價可以采用兩個指標：最大彎曲度和曲直比。最大彎曲度是指一條路線內各跡點至錨固段的最大偏離度，由最大彎曲矢量與路線長度之比的百分比來度量。曲直比是指錨固段的曲線里程數與首尾兩點直線距離的比值。這兩個指標越大，道路彎曲度越大，對線性插值計算越不利。曲直比為1時，表示道路線形為直線，這時采用線性插值轉換計算可視為無誤差。

線性插值法原理簡單但精度較低，只可滿足基本交通應用需求[11]。兩點在參考橢球面的近似直線距離為:

(1)

其中d為兩點間近似距離(單位為m)；c為1秒地心角對應的橢球面弧長，其近似值為30 m；(b1,l1)、(b2,l2)分別為點1和點2的緯度與經度，坐標單位需由(° ′ ″)轉換為(″)。插值點i到錨固段起始點的里程Ki為:

(2)

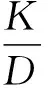
(3)

其中(b1,l1)為錨固段起始點坐標；(b2,l2)錨固段終點坐標，K為錨固段的里程數。式(1)—式(3)是基于錨固段近似為直線推導的，僅適用于直線路段。

1.3 空間曲線擬合

實際上，大部分路段是遠距離大半徑的曲線路段，線性近似會帶來很大的轉換誤差。基于道路曲線要素的動態分段模型算法[12]計算精度較高，但道路線型參數缺失時，在實現過程中會面臨很多困難[13]，且計算復雜不利于高效快速轉換。采用道路設計的曲線元素如緩和曲線、圓曲線來表示曲線路段較合理，但在現實中特別是舊路改造時，通常會面臨曲線元素與方位參數缺失等問題。因此需采用其它參數方程對曲線路段進行擬合，建立線性參照系統里程數與大地坐標的函數關系，空間曲線用以下參數方程來描述：

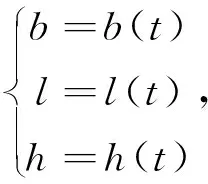
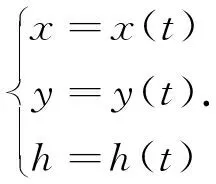
(4)

其中(b,l,h)分別為空間點的緯度、經度、大地高；(x,y,h)分別為空間點的高斯平面坐標與正常高，t為里程數變量。分段3次樣條函數可用來擬合道路平面線形[14-16]，(b,l,h)或(x,y,h)可采用分段3次樣條函數來擬合：

f(t)=c3(t-t1)3+c2(t-t1)2+c1(t-t1)+c0.

(5)

其中c0,c1,c2,c3為待求的模型系數；t1為區間[t1,t2]的起始點。

根據實測點進行分段，每段都有各自的模型系數。3次樣條函數在每個子區間上建立一個3次多項式，在分隔點處的插值等于觀測值，在分隔點處具有連續的一、二階導數，且滿足自然邊界條件；在節點處具有連續性，插值曲線為光滑分段多項式[17]。

由于里程數是單調遞增的，不會多值重復，因此區間分段是可行的，由里程數轉換到大地坐標不存在多值性。反之，由大地坐標轉換到線性參照系時，由于道路線形可能出現回旋，如立交橋在立體交叉時具有相同平面坐標的點，是空間上不同的點[4]。路面中心線軌跡的大地坐標不滿足單調性條件時，需要根據具有單調性的另一維坐標，例如高程h，建立與里程數t的函數關系，實現逆向轉換，或進行必要的分段處理。

t=f(j)|j∈ b, l, x, y, h, r.

(6)

其中f(j)與式(5)形式上相同，j是b,l,x,y,h,r(r為坐標點到區段起始點的向徑)中的任何一個具有單調性的坐標或向徑，要求該數值在整個區段單調增或單調減，不得有重復值，從而建立與里程數的一一對應關系。

1.4 計算流程

1.4.1 大地坐標系轉換到線性參照系

1)建模數據點坐標與里程實測，大地經緯度坐標由(°)(′)(″)轉換為以(″)為單位；

2)取大地坐標中具有單調增或單調減特性的某一維坐標或向徑，由分段3次樣條函數式(5)～式(6)建立與里程數的對應關系，求得模型系數；

3)根據待轉換點的大地坐標和轉換模型系數，將其轉換到線性參照系里程數。

1.4.2 線性參照系轉換到大地坐標系

1)建模數據點坐標與里程實測，大地經緯度坐標由(°)(′)(″)轉換為以(″)為單位；

2)里程數是單調增的，采用式(4)—式(5)分別建立里程數與3維大地坐標的分段3次樣條函數模型，每一維坐標建立一個模型，計算模型系數；

3)根據轉換·模型系數將里程數轉換為大地坐標。

2 算例分析

2.1 實驗數據

本實例選擇某一實際曲線路段作為實驗對象，其曲直比為1.145，最大彎曲矢量為72.3 m，最大彎曲度為21%。建立轉換模型時根據道路等級和轉換精度要求，曲線路段數據點間隔應盡量小，通常以20 m為宜[15]。從實測數字地形圖中解析得到大地坐標及里程數據如表1所示，其中x,y坐標采用地方獨立坐標系，解析坐標精度為±10 cm，里程數精度為±30 cm。

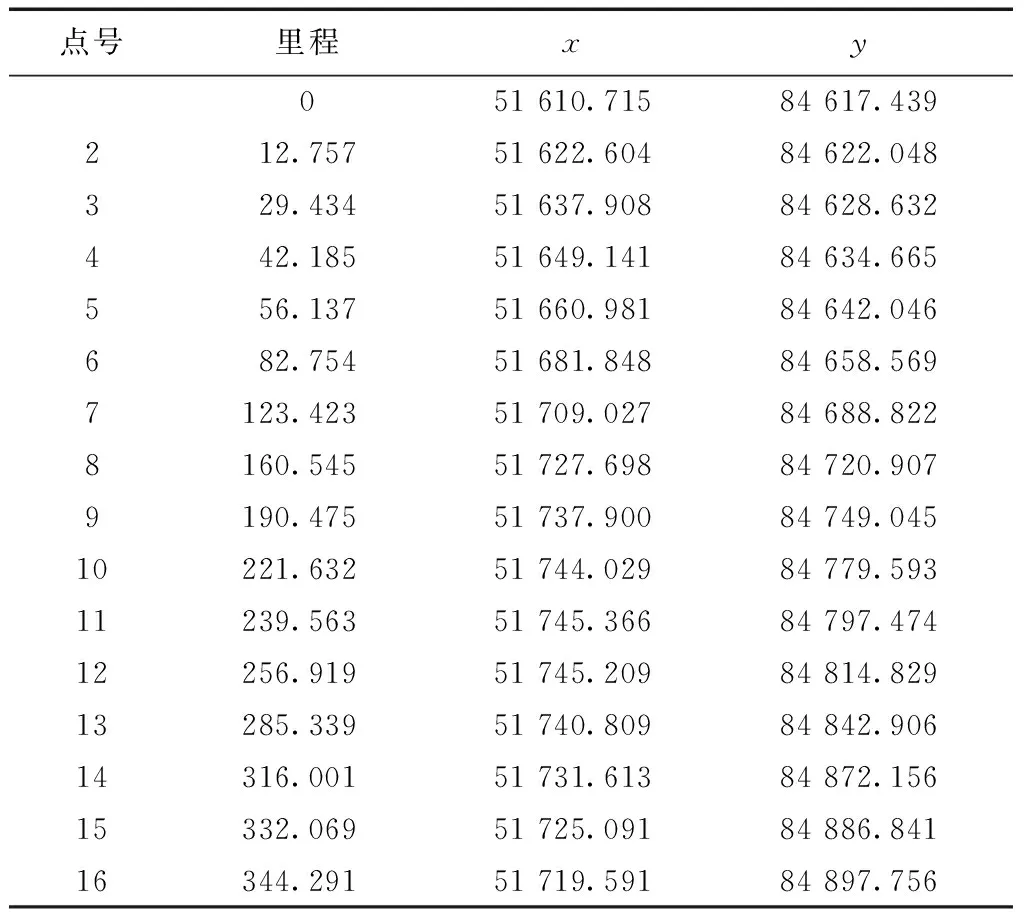
表1 大地坐標及里程表 m

2.2 大地坐標系轉換到線性參照系

將實驗點A,B,C的大地坐標轉換為以里程樁為0的線性參照系里程數，由于在該區間中x坐標不單調而y坐標單調增加，因此采用空間曲線擬合法由y坐標建立與里程數的函數關系。根據計算流程1.4.1由坐標y轉換到里程t的模型系數如表2所示。

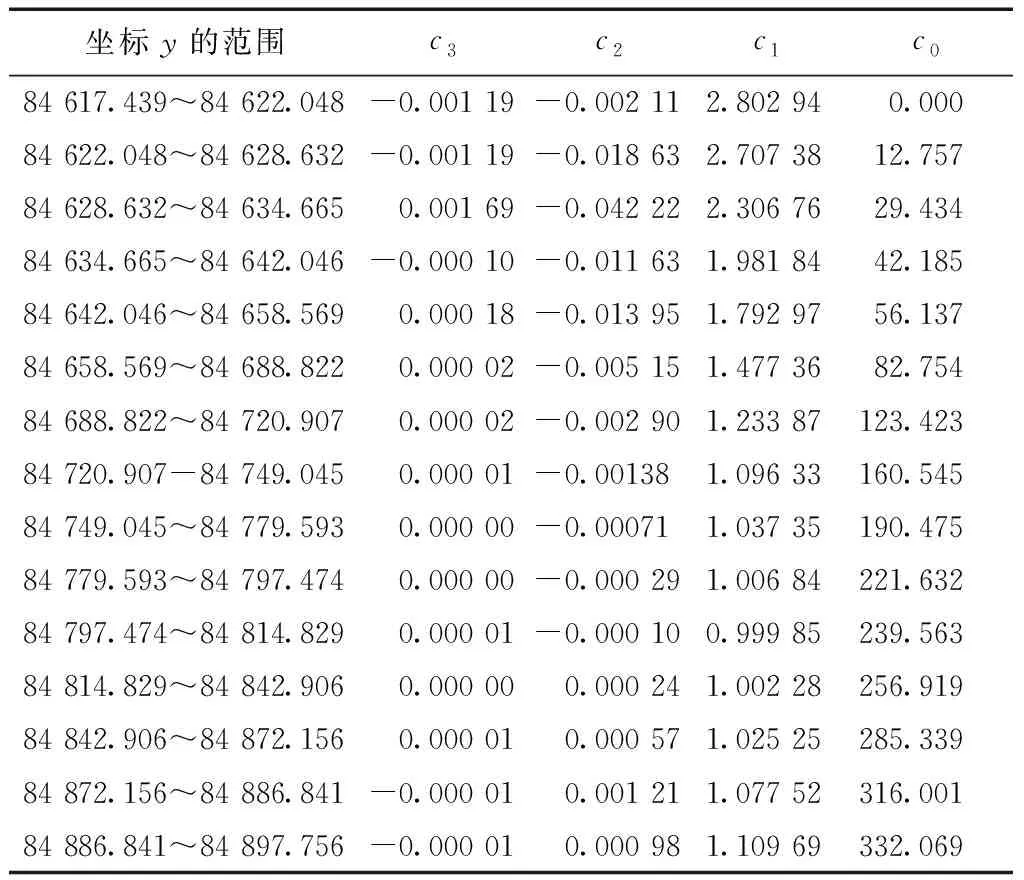
表2 分段3次樣條函數t=f(y)模型系數

根據模型系數得到轉換計算結果如表3所示，其中轉換里程與實測里程差值最大為0.543 m。

表3 大地坐標轉換到線性參照系計算結果 m

2.3 線性參照系轉換到大地坐標系

將實驗點A,B,C的線性參照系實測里程數轉換為大地坐標，根據計算流程1.4.2，由里程t轉換x坐標的模型系數如表4所示。

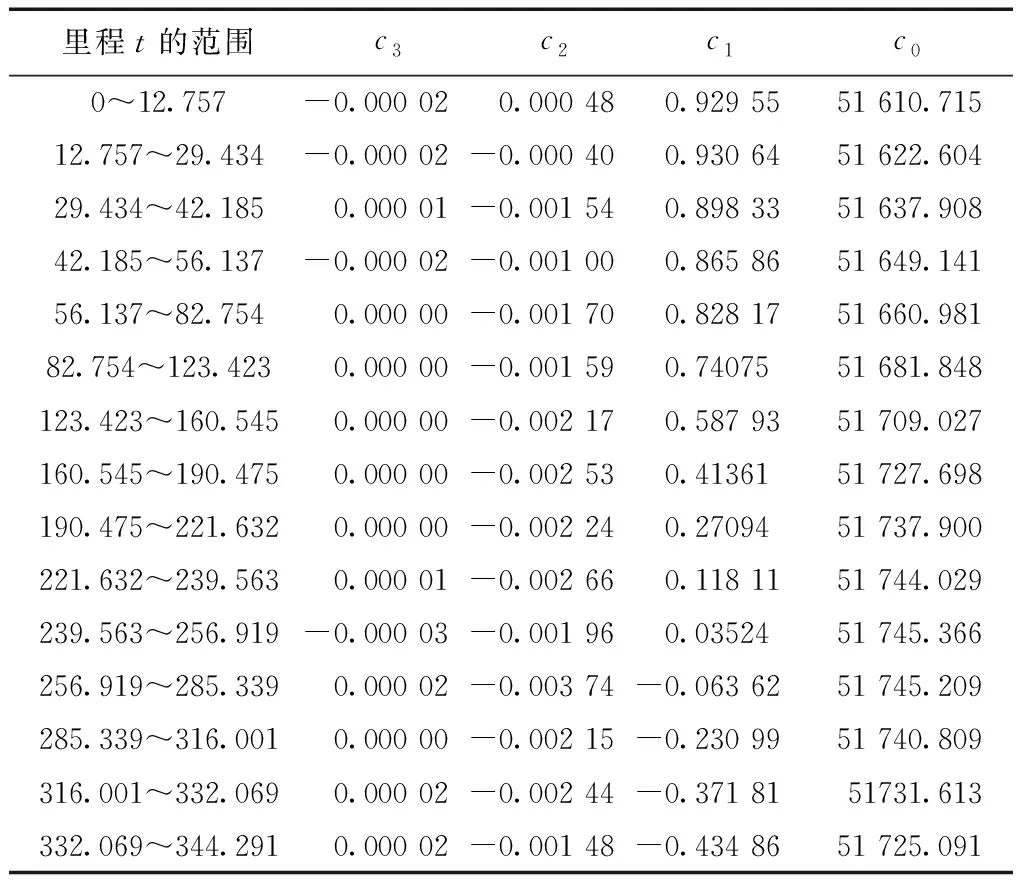
表4 分段3次樣條函數x=x(t)模型系數

由里程t轉換y坐標的模型系數如表5所示。

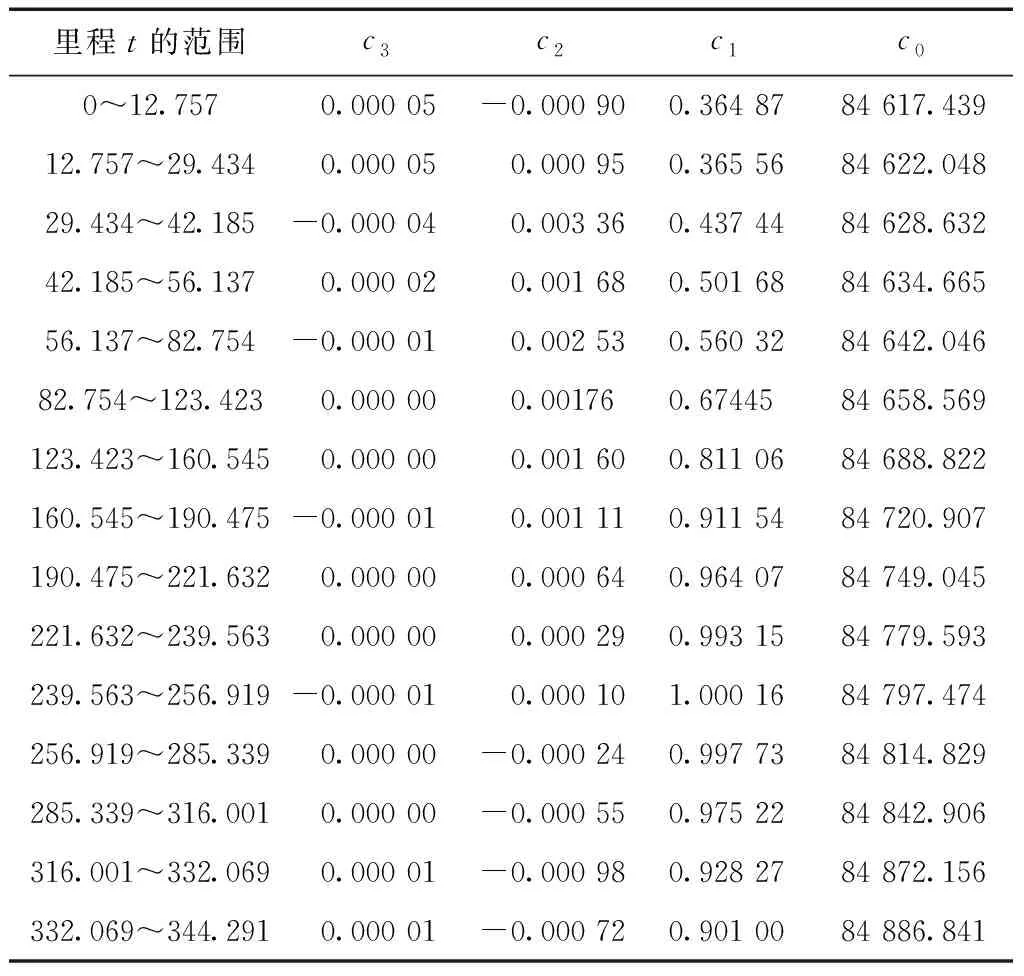
表5 分段3次樣條函數y=y(t)模型系數

由表4、表5可知，3次項系數c3接近為0，表明該曲線段采用二次樣條曲線擬合即可。由模型系數計算得到大地坐標轉換結果如表6所示，其中坐標轉換誤差最大為0.402 m。

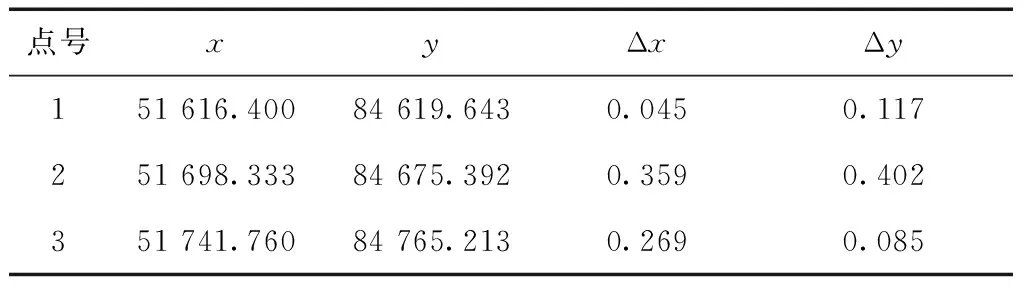
表6 線性參照系轉換到大地坐標系計算結果 m

直線路段轉換試驗分析結果表明，在直線路段3次樣條函數c3,c2的值近似為0，與直線方程等價，因此分段3次樣條函數同樣適用于直線路段的轉換。采用分段3次樣條函數，針對復雜道路線形不要求函數有較強的擬合能力，擬合曲線也不會在數據點間產生多余的擺動，轉換結果滿足交通應用需求。

3 結 論

線性參照系與大地坐標系的相互融合與高效轉換，是智能交通信息系統的一項基礎工作，適用于解決道路特征點的空間定位問題。本文在兩坐標系之間建立函數關系進行直接相互轉換，給出度量道路彎曲度的兩個指標，及兩坐標系相互轉換的兩類方法，即線性插值法和分段3次樣條曲線函數模型法。分段3次樣條函數法對直線和曲線路段都適用，要求建模數據點具有一定的密度且能反映道路線形特征，數據點密度較高且實測精度高時模型誤差可忽略。本文實驗結果顯示，線性參照系統與大地坐標系的相互轉換誤差可達±0.5 m，主要誤差來源于坐標和里程數據的測量誤差。