基于Alpha穩定分布的地面動目標檢測技術

， ， ， ，

(南京航空航天大學雷達成像與微波光子技術教育部重點實驗室， 江蘇南京 210016)

0 引言

多通道SAR/GMTI系統能在全天時、全天候地獲取高分辨SAR圖像的同時，實現地面動目標檢測及跟蹤，已成為戰略情報偵察和戰場監視的重要發展趨勢[1-3]。

20世紀末[4]，德國的Ender首先將空時自適應處理(STAP)算法引入多通道SAR系統中，并提出了SAR-STAP概念及MSAR(Multichannel-SAR)處理算法，通過空、時兩域級聯處理對雜波進行抑制，進一步提高慢動目標輸出信雜噪比(SCNR),能夠獲得更低的系統最小可檢測速度(MDV)。上述優勢使得此類算法獲得了學者們廣泛關注，經過潛心研究，已提出如特征對消算法[4]、聯合像素法[5]、ACSI技術(圖像域ADPCA技術)[6]等SAR-STAP處理算法。此類方案在理論提出時，均假設雜波及噪聲背景為(復)高斯分布。但隨著現代SAR/GMTI系統中SAR傳感器分辨率的提高，分辨單元的縮小使中心極限定理不再適用，與此同時，所探測場景類別也不斷增加，部分場景雜波數據統計特性不再服從(復)高斯分布。實際雜波統計特性與理論模型的沖突必將引起原有SAR-STAP算法在實際處理中的性能下降。

因此，必須尋找新的統計模型來刻畫非高斯雜波，并在此基礎上提出新型SAR-STAP算法。在眾多非高斯雜波統計建模方案中，Alpha穩定分布[7]是滿足廣義中心極限定理的唯一的一類分布，其概率密度具有明顯的長拖尾性質，能較好地描述雷達非高斯相關雜波[8-10]。因此，本文采用Alpha穩定分布對待檢測區域雜波進行建模，并提出基于分數低階矩的新型雜波抑制算法。與原有的SAR-STAP處理算法相比，新算法能夠在非高斯雜波背景中獲得良好的檢測性能，且具備較強的魯棒性。本文通過仿真及多組實測數據處理結果對算法進行了驗證。

1 多通道SAR-STAP技術

多通道SAR-STAP技術由沿航跡排列的N個通道接收信號，分別獲取各接收通道的距離-多普勒圖(或SAR圖像)后，逐像素單元根據最小均方無畸變(MVDR)準則計算各通道加權系數，在圖像間進行空域加權處理，實現雜波抑制。其原理如圖1所示。

N通道SAR數據某一像素單元的接收信號可由N×1維列向量(空域快拍)表示為

(1)

式中，γ，s分別為動目標的幅度和導引矢量，c為雜波分量，n為噪聲分量。根據MVDR準則，通過拉格朗日乘子法求解可得使輸出信雜噪比(SCNR)最大的最優權矢量為

wopt=γR-1s

(2)

式中，R為雜波及噪聲分量的自相關矩陣。則此濾波輸出為

(3)

由于在實際處理時，雜波及噪聲的統計特性未知，某一距離門的雜噪協方差矩陣往往由其極大似然估計(MLE)形式代替，即

(4)

式中，xl為與待檢測單元相鄰樣本信號，L為樣本個數。

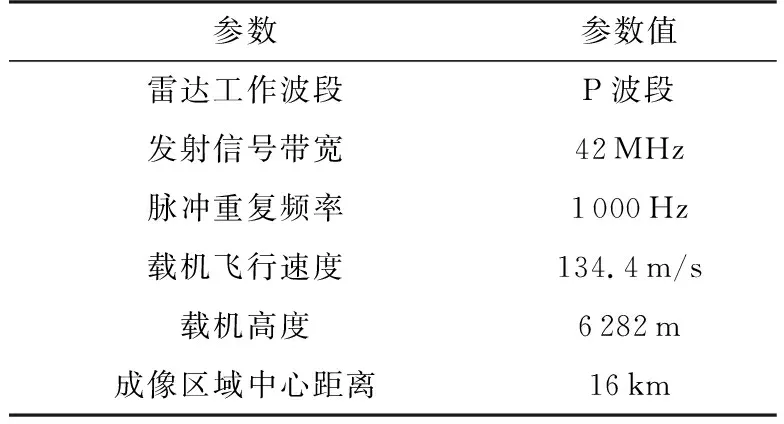
為對算法性能進行驗證，采用該算法對某型機載三通道SAR系統的一組實測數據進行了處理，表1給出了部分系統參數，處理中選取的訓練樣本數為32個(遠大于空域自由度的2倍)。圖2、圖3分別給出了數據在空域處理前單通道SAR圖像以及空域處理后的雜波抑制輸出結果。從SAR圖像中可以看出，該場景對應的區域存在建筑群，因此存在較多的強散射點雜波。而從雜波抑制結果中可以明顯看出存在大量的雜波殘留，實際的雜波抑制性能遠遠小于理論效果。

表1 三通道SAR系統參數

為尋找導致上述結果中雜波抑制性能與理論值之間的差異的原因，對該區域實測數據作進一步分析，在圖4中給出了數據幅度直方圖。首先采用瑞利分布對實測數據的幅度進行擬合，結果如圖4所示，可以看出實測數據尾部已明顯偏離瑞利分布，即該雜波背景體現出較強的非高斯性。由于上述SAR-STAP算法提出的前提即為雜波背景服從高斯分布，故采用該算法對數據進行處理必然存在性能損失。因此，尋找合適的統計模型對實際非高斯雜波進行描述，并在此基礎上提出新型SAR-STAP算法，是解決上述問題的關鍵途徑。

2 基于分數低階矩的SAR-STAP雜波抑制算法

為解決雜波理論模型與實際不符導致的雜波抑制性能下降，需尋找新的非高斯統計模型來刻畫雜波。目前已經有一些針對非高斯雜波模型的研究，如韋布爾分布、K分布、廣義Gamma分布、Alpha穩定分布等[11]，其中Alpha穩定分布可調整參數逼近其他分布，而在采用Alpha穩定分布擬合雜波數據時發現，與高斯分布相比其統計特性與數據更為吻合。因此，若將Alpha穩定分布統計模型引入SAR-STAP算法中，導出新算法實現雜波抑制，必將提高原有SAR/GMTI系統的性能。本節將給出新算法的推導過程，并采用仿真實驗對算法性能進行驗證。

2.1 基于Alpha穩定分布的雜波統計模型

在實際環境中，許多雜波噪聲源是非高斯的，此類信號完全可以采用具有穩定性質且同時滿足廣義中心極限定理的Alpha穩定分布建立統計模型[9]。

然而，由于Alpha穩定分布的概率密度函數沒有閉合解，故一個服從Alpha穩定分布的隨機變量X可用其特征函數描述為

E(exp(iωX))=

(5)

式中，0<α<2為特征指數，δ>0為離差，類似于方差，-1<β<1為對稱參數，-∞<μ<∞為位置參數，sign(·)為符號函數。當β=0時，此分布被稱為對稱Alpha穩定(SαS)分布，當且僅當隨機變量X1和X2為聯合SαS分布時，復隨機變量X=X1+jX2服從SαS分布。當α=2時Alpha穩定分布退化為高斯分布，但隨著α的減小，分布的非高斯性變得明顯，其拖尾越長。對于第2節中所給實測數據直方圖，采用Alpha穩定分布進行擬合，可得α取1.3，如圖4中實線所示，擬合效果明顯優于瑞利分布。

由于非高斯Alpha穩定分布中不存在不小于α的高階統計量，使得二階統計量及高階統計量理論不再適用。這就使得文獻[12]提出的分數低階矩理論成為研究此類非高斯相關隨機變量的有力工具。一個復SαS分布隨機變量X，其p階統計量可以表示為

E(|X|p)=C1(p,α)δp/α,-1

(6)

式中，C1(p,α)為與p和α相關的常數，可表示為

C1(p,α)=2p+1Γ((p+1)/2)Γ(-p/α)/

(7)

式中，Γ(-p/2)為Gamma函數。

2.2 基于分數低階矩的SAR-STAP雜波抑制算法

在Alpha(α<2)穩定雜波環境中不存在二階統計量，只能采用基于分數低階矩的雜波抑制算法進行處理。故可將最小方差無畸變(MVDR)準則的思想進行推廣，導出分數低階矩最小無畸變(FrMVDR)準則，并在此基礎上提出基于分數低階矩的SAR-STAP雜波抑制算法。

定義隨機變量x的冪變換為

(8)

將該變換用于通道數為N的多通道SAR圖像某像素單元的空域快拍x，可得

每個作業現場派駐一個專職安全監督員，負責每天早晨組織班前安全會，監督開展STA（安全工作分配），簽字確認STA（安全工作分配）、PTW（作業許可）、車輛設備日檢日查，并對風險預防措施落實情況、現場安全施工情況等進行全時段監督，確保生產作業過程安全受控。

(9)

則其加權輸出可表示為

(10)

式中，w=[w1,w2,…,wN]T為權矢量。式(10)稱為分數低階響應，其分數低階輸出功率可表示為

E{|y|2}=wHE{x〈p〉|x〈p〉|}w=wHR〈p〉w

(11)

式中，

(12)

可見，當p=1時，式(12)即為傳統的協方差矩陣。可以證明當p<α/2時，矩陣R〈p〉是有界統計量[13]。因此FrMVDR準則可表述為

(13)

采用拉格朗日乘子法求解可得在FrMVDR意義上的最優權矢量為

(14)

在實際處理中，矩陣R〈p〉由相鄰距離單元的訓練樣本估計所得，即

(15)

式中，L為訓練樣本數，參數p的設置同樣需要從數據中估計所得，具體方法為：對實測數據直方圖進行擬合估計α的值，選擇合適的p使得p<α/2。最終處理器所采用的權矢量表示為

(16)

該算法的信號處理流程如圖5所示。

2.3 仿真分析

本小節將采用仿真實驗對本文所提算法的雜波抑制性能進行驗證，并與原有SAR-STAP算法進行比較，實驗參數如表2所示。圖6給出了兩種算法的自適應天線方向圖，圖中所有曲線均為500次Monte-Carlo實驗的平均結果。從圖6(a)中可以看出，當α=2時(即高斯雜波背景條件下)兩種算法性能基本相同，兩條曲線幾乎重合，都能夠在目標多普勒位置形成高增益，同時在雜波多普勒中心位置形成凹口。而從圖6(b)、圖6(c)、圖6(d)可以看出，隨著α的減小，原有算法自適應方向圖在雜波中心位置凹口深度明顯變淺，雜波抑制性能顯著下降，與之相比，無論是在雜波還是信號方向新算法都能獲得較為理想的性能。

表2 仿真實驗系統參數

在上述實驗基礎上，通過仿真方法生成三通道SAR系統單個多普勒單元的512個距離門的雜波數據，并在其中添加3個動目標信號，分別位于第127，255，384距離門。隨后，采用本文算法及原有SAR-STAP算法對數據進行處理，并在圖7中給出了雜波抑制結果。此次仿真中，目標信噪比設為20 dB，其他參數同前，所有結果均為500次Monte-Carlo實驗的平均值。

可以看出，在α=2時即高斯環境下兩種算法性能基本相同均能實現雜波抑制，但隨著α的減小，基于傳統MVDR的算法性能明顯下降，在α=0.5時已經無法實現雜波抑制；而基于FrMVDR的雜波抑制算法性能雖然有所下降但仍然可以有效完成雜波抑制。

上述結果表明，在非高斯干擾明顯的環境中，原有算法性能會急劇下降甚至失效，但基于Alpha穩定分布的新算法可以有效完成雜波抑制，為接下來的動目標檢測奠定基礎。

3 實測數據處理結果

實際處理中，隨著SAR圖像的分辨率不斷提高，從圖像中可以看出更多的細節特征，部分成像場景中能清晰地觀察到城市中的建筑群等強雜波散射點，此類SAR圖像將呈現出明顯的非高斯性。因此，若采用基于Alpha穩定分布的雜波抑制算法進行處理，必能提高系統的GMTI性能。

圖8給出了第2節中實測數據采用新算法進行雜波抑制的處理結果，處理過程中p略小于α/2取0.6。可以看到在采用基于FrMVDR的雜波抑制算法處理后，雜波強散射點得到了有效的抑制，處理結果明顯優于原有算法。對兩個處理結果分別作CFAR檢測，虛警概率設為10-6，結果如圖9所示，圖中黑點表示該像素單元為虛警點，可見新算法的虛警數明顯低于傳統算法。

為進一步驗證新算法的性能，采用此算法對另一組某型機載四通道SAR數據進行處理，表3給出了數據的部分系統參數。在處理時，首先對數據進行擬合，估計可得參數α為1.29，擬合結果如圖10所示。圖11為檢測區域SAR圖像，從圖中可以看到局部區域存在大量強散射點。雜波抑制處理過程中p略小于α/2取0.6，可見原有算法處理結果局部區域有著明顯的雜波殘留，如圖12所示，圖13給出了虛警概率為10-6的CFAR檢測結果，圖中黑點表示該像素單元為虛警點，可以看到該區域中虛警數嚴重增多。與之相比，新算法處理后這些區域可獲得理想的雜波抑制效果。

表3 四通道SAR系統參數

為進一步對新算法進行驗證，在該四通道數據中添加仿真動目標。每次試驗均在此塊區域內添加40個運動參數不同的仿真動目標，采用兩種算法分別進行雜波抑制，在保證具有相同的目標檢測數的情況下，檢測結果如圖14所示，圖中空心點表示目標點，黑點表示虛警點。限于篇幅，僅給出其中一次檢測結果圖，將其余各次實驗結果列于表4。從表4中可以看出，新算法可有效抑制非高斯雜波減少檢測結果的虛警數，同時保證系統的檢測性能。

表4 仿真目標檢測結果

4 結束語

本文針對復雜探測場景中雜波分布偏離高斯分布的情況，采用Alpha穩定分布建立雜波模型，并在此基礎上提出了基于分數低階矩的SAR-STAP雜波抑制算法。文中通過對仿真實驗及多組多通道SAR實測數據處理對算法性能進行了驗證，結果表明，該算法在非高斯環境中性能明顯優于原有算法，并表現出良好的魯棒性，是一種實用且有效的多通道SAR雜波抑制算法。