利用Alpha-shape算法進行樹冠三維模型構建

李 慶，高祥偉,費鮮蕓，張 紅，王 健，崔云健，李 彬

(淮海工學院測繪與海洋信息學院，江蘇 連云港 222002)

樹冠是森林生態(tài)系統(tǒng)的基本構成，樹冠結構(如體積、表面積、疏密度、分枝特性)與樹木光合作用潛力密切相關，是指示樹木生長狀況的重要指標[1-3]。三維激光掃描技術作為一種新型的測繪技術，能夠高精度采集樹木的三維點云數據，為樹冠三維模型構建及林分結構計算提供有力的支持。但是由于樹冠內部存在大量不規(guī)則空洞，以及樹枝的相互遮擋，利用三維激光點云數據進行樹冠三維建模、樹冠內部結構參數計算尚存在難點[4-6]。

目前可用于計算樹冠體積的三維模型主要有兩種：①幾何模型。戴超[7]利用快包法構建樹冠點云的最外凸包模型；熊妮娜等[8-11]先后將樹冠模擬為圓錐、圓臺等規(guī)則幾何體或不規(guī)則臺體的疊加。這些幾何模型主要以計算樹冠外包體積為主，樹冠點云內部的無效容積無法消除，對于冠層內部疏密、分枝特征表現不足，計算得到的結構參數也較單一，無法全面地指示樹木冠層內部形態(tài)。②體素模型。吳賓等[12-13]先后建立體素模型，將待測空間分割為體素，包含激光點的有效體素個數乘以體素體積即得總體積。這種模型在樹冠枝葉茂密時易受內部點云缺失影響，模型易形成內部空洞，也無法全面地指示樹木冠層內部形態(tài)。

alpha-shape算法由Edelsbrunner[14-15]首先提出，最初用于點集輪廓的構建。目前該算法已被應用于網格生成、醫(yī)學圖像分析和可視化的地震數據結構等，也被應用于建筑物頂面輪廓的邊緣提取[16-17]，但如何利用alpha-shape算法提取樹冠散亂點云輪廓，進行樹冠三維模型構建還缺少深入系統(tǒng)的研究。

本文將alpha-shape算法應用于復雜樹木的模型重建，并通過對參數α大小的控制，對樹冠進行三維模型重建；分析不同參數α時，所構建樹冠三維模型的空間指示特征為樹冠內部結構參數的計算準備基礎。

1 樹種選擇

櫸樹在連云港市屬于鄉(xiāng)土綠化樹種，被廣泛用于城市綠化建設，在連云港城市綠化樹種中具有代表性，在淮海工學院校內也作為重要的綠化樹種廣泛種植。目前校園內生長有不同樹齡、不同胸徑的櫸樹，為研究提供了豐富的可選樣本。

本次研究選取連云港市淮海工學院校內20棵櫸樹為樣本，數據測量信息見表1。為了減少葉片對樹木內部遮擋而造成的點云缺失的影響，本研究選擇在冬季樹木落葉時進行掃描測量。

表1 樣本數據統(tǒng)計指標 m

2 研究方法

2.1 數據采集與預處理

本文以徠卡ScanStation C10三維激光掃描儀作為數據獲取平臺，采用基于標靶的方法采集中等分辨率的點云數據，并利用Cyclone軟件實現數據配準和去噪處理。以一棵樹為例，樣本的真實照片和預處理后的櫸樹點云數據如圖1所示。

2.2 alpha-shape算法及其參數α

alpha-shape算法適合從一堆無序的點集中提取物體的邊緣。算法原理如下：假設有一點集P，其alpha-shape是一個由點集P和半徑參數α決定的唯一多邊形。如圖2所示，可設想成存在一個半徑為α的圓，從點集P外某一點開始滾動，若α足夠大，那么這個圓就不會滾到點集P的內部，則這個圓滾動的痕跡就是點集P的邊界線。若α很大(α→∞)時，則檢測出的邊界線是點集P的凸包。同理，三維空間的alpha-shape算法則是通過三點作半徑為α的球來判斷邊界點，并在得到的邊界點處建立三角片面，重構出曲面。alpha值的設定直接影響三角形表面的重建結果，參數α控制了多面體生成的精細程度[18]。

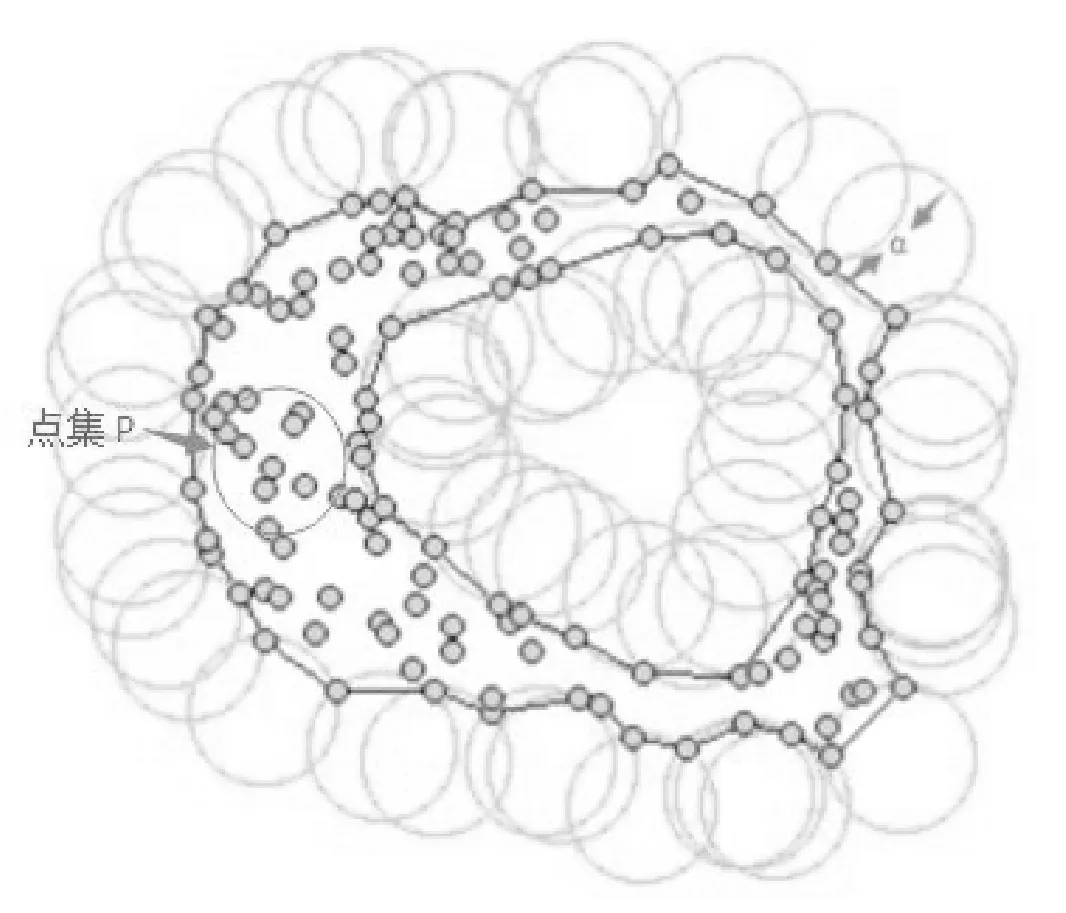
圖2 alpha-shape算法示意圖

本文在Matlab環(huán)境下，利用alpha-shape算法，通過不斷調整α參數的取值，對20棵樣本櫸樹進行三維建模。根據試驗效果，以α值選取0.01、0.02、0.03、0.04、0.05、0.06、0.07、0.08、0.09、0.1、0.25、0.5、1、10為例進行說明，通過三級樹木枝條建模效果、樹冠體積變化特征對運算結果進行分析評價。

3 結果分析

3.1 不同α參數樹冠三維建模目視分析

以參數α分別取10、0.1、0.05、0.02及0.01時為例，對基于alpha-shape算法構建的三維模型進行目視分析，圖3為樹木冠體以及主枝、細枝的正視建模效果。

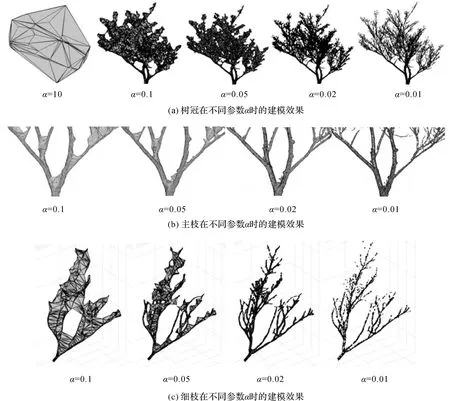
圖3 三維模型效果

從圖3可以看出，當參數α=10時，樹冠結構被高度綜合，生成的模型是最外部點云構成的凸包，此時模型對樹冠內部結構無法表達，樹枝無法重建；當α=0.1時，模型可以較好地表示樹木冠層的凹凸不平曲面；當α=0.05時，曲面重建效果較差；當α=0.02時，三維結構其重建結果較為精細，樹冠的幾何結構和拓撲結構表達效果較好，樹木主枝及細小枝條曲面重建效果較好，可以獲取較精細的三維模型；但是當α取值過小時，如α=0.01，不能找到足夠的點來組建曲面，因此得到的圖形是一些離散的面片，重建結果不完整，會出現較多的孔洞。

通過調整α值，構建出的模型能夠反映樹冠在空間伸展時不同的形態(tài)、表面積、分枝特性、疏密程度等特征。因此，利用alpha-shape算法對樹冠進行三維重建時，利用不同的參數α可以構建出樹冠不同的空間形態(tài)特征。

3.2 不同α參數樹冠體積分析

3.2.1 常用算法及不同α參數求得的樹冠體積

由于目前樹冠體積的真值無法獲取，本文將取不同參數α值時樣本樹冠體積計算結果與快包法[7]計算結果進行對比，分析α值對樹冠模型重建的影響。計算結果見表2，同時，分別計算alpha-shape算法不同參數α時的樹冠體積與快包算法所得體積的相對差值均值及相關系數。

從表2可以看出，當α=10時，兩種方法計算的樹冠體積值趨于相等，樹冠體積的alpha-shape算法與快包法算得的樹冠體積平均相對誤差為0.007，二者的相關系數高達1。而隨著α的減小，alpha-shape算法獲得的樹冠三維模型包含的樹冠孔隙越來越多，求得的體積也逐漸減少，兩者的差值越來越大；相關性越來越小，當α=0.02時，平均相對誤差值可達0.995，二者的相關系數只有0.101，也進一步說明精細模型能夠較好地構建樹冠內部結構，由于內部分枝特性不同，相同的外包模型內部結構差異較大。

3.2.2 樹冠體積與樹木物理參數相關性分析

將不同α參數下求得的樹冠體積與冠幅、冠高、胸徑進行相關性分析，統(tǒng)計結果見表3。

由表3可見，當α=10時，最外層樹枝點云包圍形成的體積不能反映樹冠結凹凸不平，但可以反映整個樹冠在空間的伸展形態(tài)，此時求得的樹冠體積與冠幅、冠高相關性明顯。隨著α的減小，由于樹冠三維模型逐漸接近樹冠真實形狀，不同的樹木之間樹冠結構差異對體積計算影響也越來越大，因此樹冠體積與冠幅、冠高相關性逐漸減少。當α=0.02時，得到的樹冠三維模型較精細，受內部結構變化的影響，此時二者在樣本間已沒有相關性。

還可以看出，胸徑與樹冠的三維體積的相關性明顯區(qū)別于冠幅和冠高，不同參數α的樹冠體積與胸徑相關系數都較大(0.01時除外，此時構建的三維模型較離散，結構不完整)，而且該相關性在α=0.1時達到最大，此時的冠體模型由樹冠的凹凸表面構成。

取不同參數α時構建的樹木三維模型反映了樹冠的不同空間形態(tài)特征，進而可用于指示樹冠參數的研究，而相關參數的指示意義需要進一步量化和分析，受論文篇幅的影響，相關研究需要在以后的研究中詳細開展。

4 結 語

本文利用alpha-shape算法對櫸樹激光掃描點云數據進行三維建模，并對不同參數構建的樹冠三維模型進行分析，可以得出：

參數α=10時，構建的三維模型較綜合，可以反映整個樹冠在空間的伸展形態(tài)，形狀較穩(wěn)定，但樹冠內部結構無法描述；α=0.1時，可以表現出樹冠的凹凸表面；α=0.05時，可以表現出其分枝特性；α=0.02時，可以構建出精細的三維模型，能夠較詳細地表示樹冠內部形狀、疏密程度的變化；但減小到一定值時，得到的圖形是一些離散的面片，重建結果不完整，不能形成樹木模型。

利用alpha-shape算法對樹冠進行三維重建時，在參數變化過程中，構建的三維模型也在有規(guī)律地變化；樹冠體積與冠幅、冠高、胸徑等相關性也在有規(guī)律地變化。可以看出，不同參數α構建的三維模型能夠反映樹冠的空間伸展形態(tài)、曲面體積、分枝特性及樹冠規(guī)則性等結構參數，研究結果可作為冠層結構參數計算的研究基礎，相關內容將會進一步研究。