基于AR模型的MEMS慣導隨機誤差分析方法
呂春紅 李 洋 趙 坤 董 純
北京航天自動控制研究所,北京 100854
隨著MEMS技術的不斷發展和成熟,一些低成本的炮彈、導彈和火箭彈等武器需要采用低成本的慣性器件實現自主導航。但問題是MEMS慣性器件的精度低,各項性能指標不能達到導航系統的要求,因此,為提高MEMS捷聯慣性導航系統精度,需要對現有慣性器件的誤差特性進行深入研究并建模,采用切實有效的補償方法加以消除。MEMS慣導工具誤差一般可分為靜態、動態和隨機誤差項。靜態和動態誤差一般認為是與載體運動的速度、加速度等有關的確定性誤差項,可通過試驗標定補償。而隨機漂移是陀螺的重要特性,國內外在陀螺漂移測試及建模方面做了大量工作。從陀螺的質量塊、彈簧系統等諧振結構層面建立MEMS陀螺儀的數學物理模型,然后對誤差進行補償,雖能取得較好的效果,但是在大多數情況下,由于缺乏MEMS陀螺制造結構等相關信息,大都采用時間序列統計建模等方法。其中Allan方差法是對陀螺噪聲進行分析的標準方法,它可以將各種誤差源及其對整個噪聲統計特性進行辨識。除此之外,還可采用神經網絡[1]、小波分析[2]等對陀螺的隨機誤差進行建模。文獻[3-5]給出了一般陀螺的隨機誤差典型Allan方差分布。
結合實際工程應用,描述了根據MEMS慣導輸出,采用時間序列分析方法,對陀螺進行趨勢項、平穩性檢驗及周期檢驗,然后采用基于Allan方差估計出MEMS陀螺主要隨機誤差項,建立AR模型,通過Kalman濾波對隨機誤差進行估計與補償。
1 時間序列分析方法
陀螺的隨機漂移一般是時間的函數,實際上是一個隨機過程。對于隨機過程,我們無法用時間t的確定性函數來加以描述。但是,可以借助數理統計方法,通過對大量漂移數據的統計分析,找出它的統計規律或者統計特性。
時間序列分析方法將平穩、正態和零均值的隨機序列看作是各時刻相關的序列,序列由各時刻出現的白噪聲組成,即k時刻為:
xk=φ1xk-1+φ2xk-2+…+φnxk-n-
θ1ak-1-θ2ak-2-…-θmak-m+ak
(1)
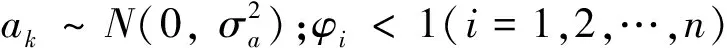
如果模型中θi=0(i=1,2,…,m),則模型簡化為:
xk=φ1xk-1+φ2xk-2+…+φnxk-n+ak
(2)
該模型稱為n階自回歸模型AR(n)。如果模型中φi=0(i=1,2,…,n),則模型簡化為:
xk=ak-θ1ak-1-θ2ak-2-…-θmak-m
(3)
該模型稱為m階的滑動平均模型MA(m)。
2 陀螺漂移數據預處理
ARMA模型要求數據{xt}是平穩、正態和零均值的時間序列。陀螺輸出的原始信號中一般包含有緩慢變化的趨勢項和隨機漂移項。所以在采用時間序列分析法進行建模前,一般需將原始信號中的趨勢項去掉。
2.1 基于二次擬合的趨勢項提取方法
一般趨勢項可以采用線性、指數等函數進行擬合。本文采用二次擬合的方法,趨勢項的函數如下:
mt=a0+a1t+a2t2
(4)
其中,a0,a1,a2為待估參數。
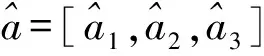
(5)
也可用差分法消除趨勢項。一階差分算子定義為:
▽xt=xt-xt-1
(6)
二階差分定義為:
▽2xt=▽(▽xt)=xt-2xt-1+xt-2
(7)
實際問題中往往需要差分的階數很低,一階或兩階就已經足夠。
2.2 平穩性檢驗
平穩性檢驗是陀螺隨機漂移數據檢驗的首要問題,它用來檢驗漂移數據序列是否具有不隨時間推移而變化的統計特性。本文采用逆序法進行平穩性檢驗。首先設定每個子樣的個數l為20,原始序列的長度為N,則子序列的長度為n=N/l。逆序總數的理論平均值為:
(8)
逆序總數的理論方差為:
(9)
通過對100個子序列進行計算,可以得出計算的逆序總數為651。利用構造的統計量計算出的u=0.6525。
從圖1可以看出,各子序列的逆序數總體是呈線性遞減的趨勢,并且在真實逆序數的上下變化。當顯著性水平為0.05時,若|u|<1.96,則說明是平穩序列。而上面計算出的u為0.6525,滿足平穩序列的要求。
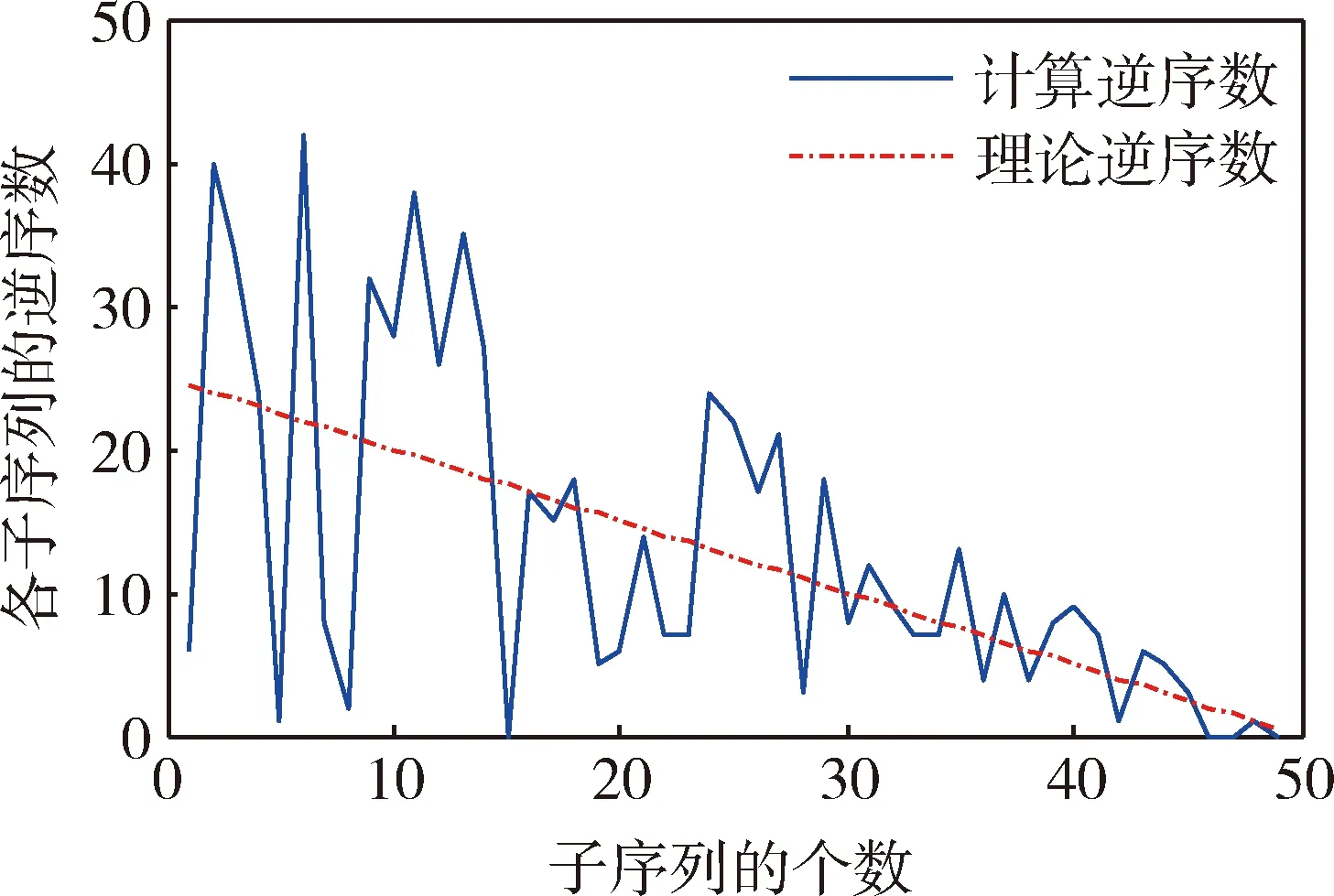
圖1 各子序列的逆序數分布圖
2.3 周期性檢驗
周期性檢驗用來識別陀螺隨機漂移數據中是否包含有隨機量以外的周期性分量,周期性檢驗的方法是直接考察從漂移數據得到的概率譜密度函數、自相關函數或功率譜密度的圖形。從圖2可以看出,功率譜密度圖中也沒有明顯的譜峰,說明陀螺的輸出中不包含有周期項。

圖2 陀螺漂移的功率譜密度
3 基于Allan方差的隨機誤差估計
將MEMS慣組放置在試驗室隔離地基上,測試軸置于水平面內東西方向,采樣頻率100Hz,采樣3000s。MEMS陀螺的原始輸出曲線圖如圖3。
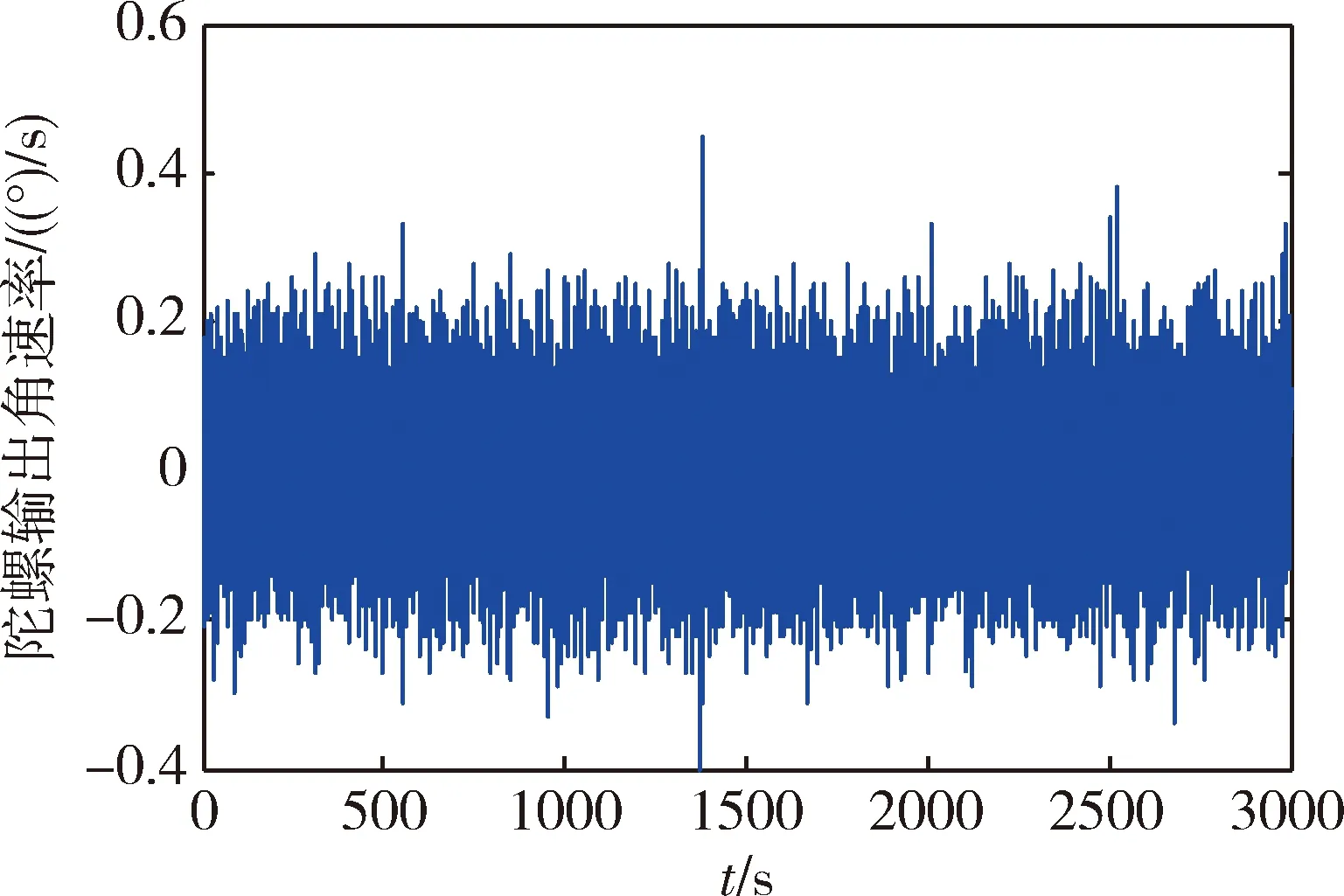
圖3 MEMS陀螺靜態輸出曲線圖
在陀螺隨機誤差中通常存在角隨機游走,速率隨機游走,偏差不穩定性,量化噪聲和速率斜坡。根據上面對5項隨機誤差的分析,總的Allan方差可以表示為5項隨機誤差的Allan方差之和,形式如式(10)[6]。
(10)
根據陀螺靜態測試數據,計算的Allan標準差與的雙對數(log-log)曲線圖如圖4所示。
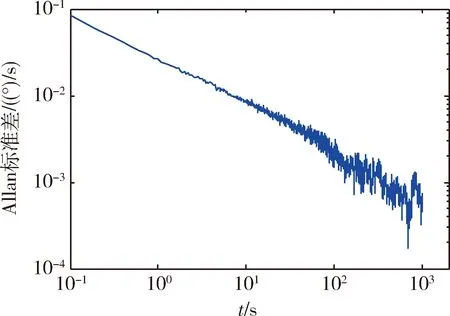
圖4 MEMS陀螺的Allan標準差曲線圖
對式(10)采用最小二乘擬合方法可計算得到角度隨機游走系數、零偏不穩定性系數、速率隨機游走系數、速率斜坡和量化噪聲的估計值,如表1所示。

表1 MEMS陀螺的各項隨機誤差估計值
從表1可以看出,該陀螺的角度隨機誤差為MEMS隨機誤差中的主要部分,其他噪聲項的系數非常小,可以忽略不計。
由于MEMS陀螺的隨機漂移模型階次比較低,一般不超過二到三階,所以在實際建模中選用了AR(1)、AR(2)和AR(3)三種時間序列模型進行討論。AR模型結構式可寫成式(2)的形式。對各參數估計得到數據如表2所示。
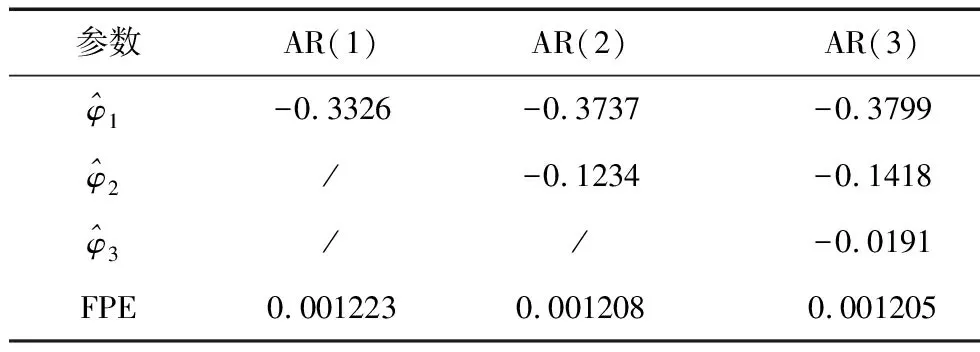
表2 AR模型的參數估計結果
采用FPE(最終預報誤差)準則分析模型定階。從表中可看出,AR(3)模型的FPE最小,但與AR(1)模型的FPE基本相同,所以可采用AR(1)模型來描述陀螺的隨機漂移模型。
上面已經確定出陀螺隨機漂移模型的類型和參數,采用AR(1)進行建模。采用所建立的模型即可進行卡爾曼濾波。AR(1)模型如式(11):
x(k+1)=-0.3326x(k)+w(k)
(11)
其中,x(k)是陀螺漂移模型的狀態,w(k)是均值為0,方差為σ2的白噪聲。
建立的卡爾曼濾波狀態方程如式(12):
x(k+1)=Φ(k,k-1)x(k)+Fw(k)
(12)
其中,Φ(k,k-1)=-0.3326,F=1。
系統的觀測值可以表示為狀態量加上白噪聲:
y(k)=x(k)+v(k)
(13)
則H=1,V(K)為白噪聲序列。
4 仿真實驗
根據上述建立的隨機誤差AR(1)模型,建立Kalman濾波方程,進行陀螺輸出隨機誤差估計。狀態方程的噪聲方差陣Q和觀測噪聲方差陣R取為AR(1)模型的估計誤差的方差。濾波誤差的協方差陣初值p(0/0)取為1,狀態量的初始值x(0)取為0。圖5為陀螺靜止時采樣1min的數據,采樣頻率為100Hz。
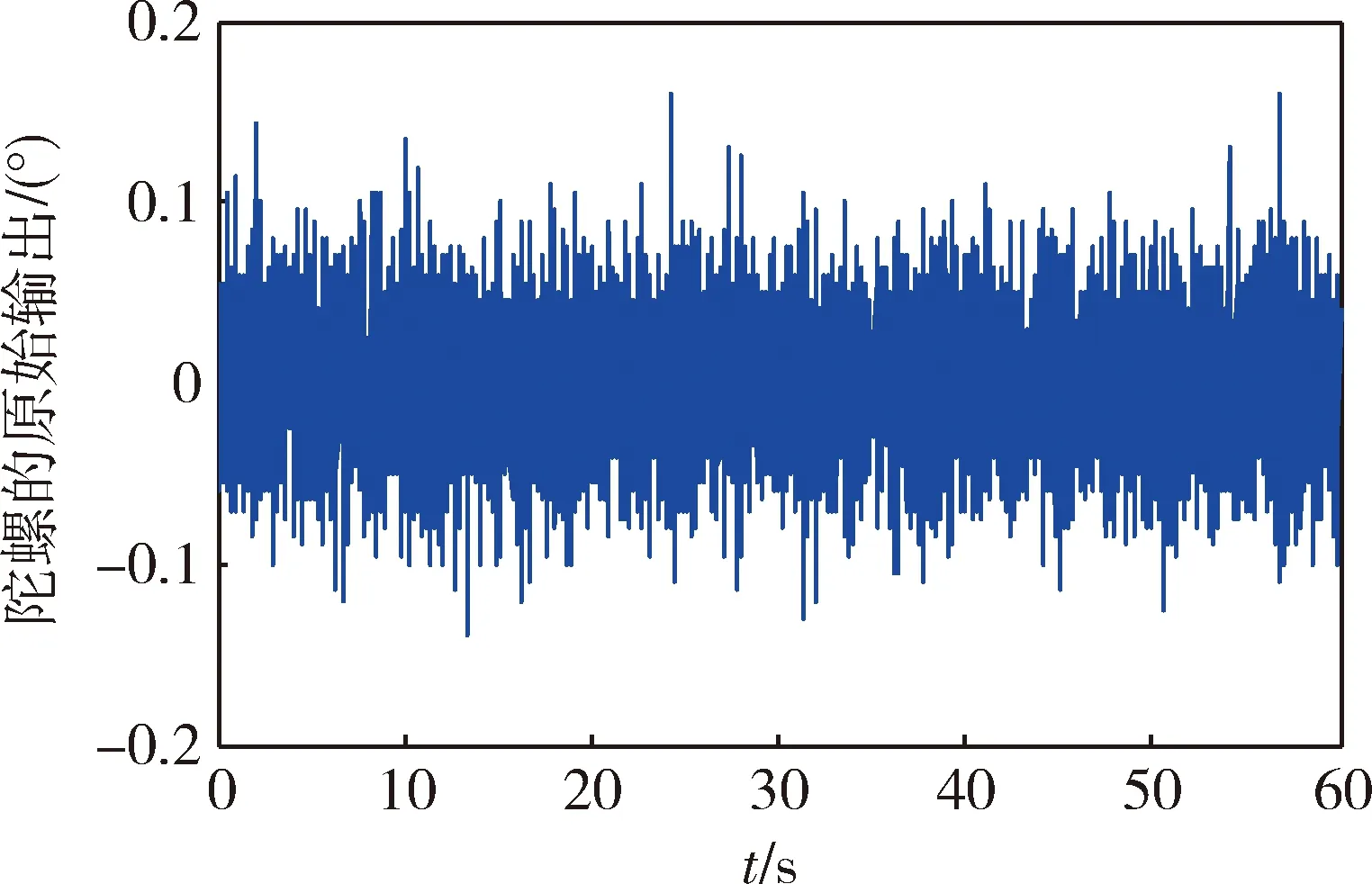
圖5 陀螺輸出的原始數據
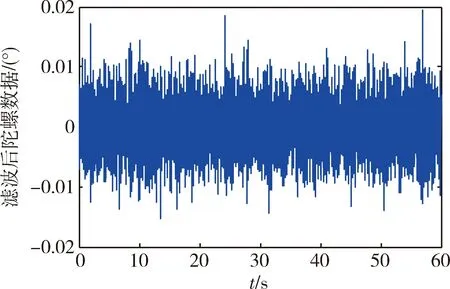
圖6 卡爾曼濾波后的陀螺輸出
圖6為Kalman濾波后的陀螺輸出曲線。濾波前陀螺輸出的原始數據的標準差為0.0143(°)/s,濾波后陀螺輸出的標準差為0.00424(°)/s,提高了3倍。
5 結論
采用Allan方差法分析了陀螺中的各項隨機誤差系數,通過時間序列方法對隨機誤差進行建模,再應用Kalman濾波可以減小MEMS陀螺的隨機誤差。仿真實驗表明采用時間序列分析進行參數估計可以有效消除MEMS慣組導航方程中的模型誤差和測量誤差,從而大大提高MEMS捷聯慣導的精度。本文是根據靜態測試數據進行隨機誤差建模,后續可以結合導彈當前運動模型,研究動態條件下MEMS慣導的隨機誤差建模與補償方法。

