“整體思想”在初中數學解題中的應用
張亞峰
(江蘇省泰州中學附屬初級中學,江蘇泰州 225300)
引 言
整體思想是指在解決數學問題時,將要解決的問題看作一個整體,通過對問題的整體形式、整體結構、整體特征進行綜合考慮后得出結論的一種解題方法[1]。整體思想的主要表現形式有整體代入、整體換元、整體構造,其在代數式的化簡與求值、解方程(組)、幾何解證等方面都有著廣泛的應用,正確地利用它來解題,可以達到事半功倍的效果。
一、在整式運算中的應用
A.7 B.18 C.12 D.9
解:因為3x2-4x+6=9,則所以
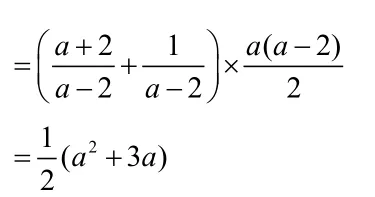
分析:如果直接代入計算,運算量非常大,觀察已知條件的特點,考慮“整體代入”。
二、在方程中的應用
分析:本題若用一般方法,即先解方程組,再代入求值,將十分煩瑣。仔細觀察發現,若將兩個方程直接相加,再化簡,則很容易得出答案。
解:將兩個方程相加,得3x+3y=15,所以x+y=5。
例6:甲、乙、丙三人參加數學競賽,競賽題目共有100道,每人都解出了60道,且每道題都至少有一人能解出。若將其中只有一個人能解出的題稱為難題,將有兩個人能解出的題稱為中等題,將三個人都能解出的題稱為容易題。試問:難題多還是容易題多?多的比少的多幾道?
分析:設共有x道難題,y道容易題,z道中等題。
由于難題只有一個人能解出,所以三人共解難題x道;容易題有三人都能解出,所以三人共解容易題3y道;中等題有兩個人能解出,所以共解中等題2z道。而本題有兩個等量關系:(1)難題數+容易題數+中等題數=100;(2)3人共解題180道。
本題要求解出難題與容易題相差多少道,可將x-y看作一個整體,設法消去z。
解:根據題意得方程組:
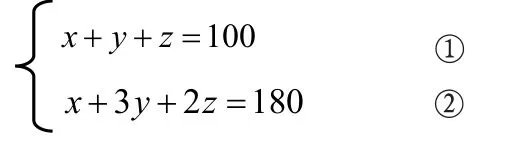
①×2-②,得x-y=20
所以,難題比容易題多,多20道。
三、在幾何計算中的應用
例7:如圖1所示,在高2米,坡角為30°的樓梯表面鋪地毯,地毯的長度至少需要_____米。
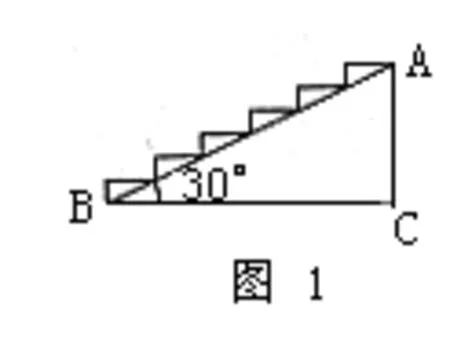
圖1 坡角為30°的樓梯
分析:由于臺階的級數以及每一級臺階的長和高都未知,無法通過求每級臺階所需地毯的長度來求地毯的總長度。若從整體考慮:將每級臺階的高都平移到AC上,就可得知各級臺階高的和恰為AC的長。同樣可得各級臺階長的和恰為BC的長。
例8:如圖2所示,五個半徑都是1的等圓⊙A、⊙B、⊙C、⊙D、⊙E相互外離,順次連結五個圓心得到五邊形ABCDE,則圖中陰影部分的面積和是( )。
A. π B. 1.5π C. 2π D. 2.5π
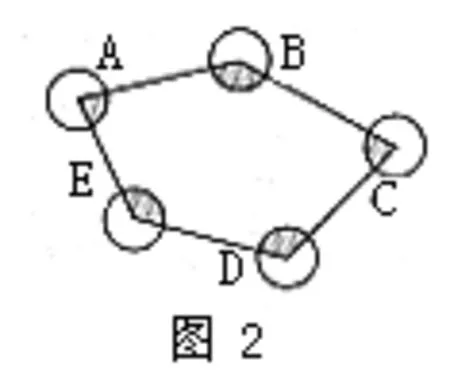
圖2 五個半徑為1的等圓
分析:由于無法求出每個扇形圓心角的度數,從而不能得到各個扇形的面積,因此要將五個陰影部分作為整體來考慮。注意到五邊形的內角和為540°,即五個扇形的圓心角和為540°,而各個扇形的半徑也相等。
例9:如圖3所示,等邊△ABC中,BC=4,AD⊥BC,點E、F是AD上的兩點,則圖中陰影部分的面積是( )。
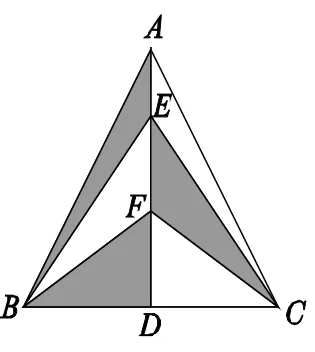
圖3 等邊三角形ABC
分析:不難看出,EFCΔ的面積等于EFBΔ的面積,可將圖中陰影部分轉變成一個整體,即ABDΔ的面積。
結 語
整體思想作為初中數學一種重要的思想方法,它能使復雜問題簡單化。布魯納指出,掌握基本數學思想和方法能使數學更易于理解和記憶。數學思想方法是數學的精髓,只有領會了數學思想方法,用數學思想方法來武裝自己,才能真正成為數學的主人。

