考慮結構面黏聚力損傷變化的洞室塊體穩定分析

駱 健， 章楊松，*， 李曉昭

(1. 南京理工大學理學院， 江蘇 南京 210094; 2. 南京大學地球科學與工程學院， 江蘇 南京 210093)

0 引言

巖體在形成和演化的過程中，由于受到各種地質作用和構造力的影響，會形成大小不一、形態復雜、分布錯綜復雜的巖體結構面，并與隧道開挖形成的臨空面組成不同規模的巖石塊體，這些塊體的失穩或垮落會破壞巖體整體的穩定性。因此,在設計階段，根據形成的結構面信息分析塊體的穩定性，對優化設計和開挖支護方案具有重要的指導意義。

由石根華[1]提出的關鍵塊體理論和P.M.Warburton[2]提出的塊體可移動性的矢量法是巖石塊體穩定性分析方法的重大突破，為用數值方法研究裂隙巖體穩定奠定了重要基礎。研究裂隙巖體穩定的方法主要有連續介質法、非連續介質法和連續-非連續介質的混合法等[3]。黃達等[4]運用數值計算軟件FLAC3D，通過連續介質法考慮塊體的變形以及塑性區分布特征來評價塊體的穩定性。張雨霆等[5-6]提出復雜巖石塊體識別的單元重構-聚合法，并進一步采用連續介質法，運用數值分析軟件FLAC3D中的Interface界面單元模擬巖石塊體穩定性。Wu等[7]提供了一種DDA(非連續變形分析)的離散化方法來計算塊體穩定性，此方法能夠模擬出塊體的掉落行為。

連續介質法的缺點是不能模擬塊體的掉落行為；在模擬具有膠結結構面的塊體失穩時，目前常用的非連續介質法無法分析其膠結面的漸進損傷過程及狀況。針對以上問題，本文采用顯式動力有限元模擬裂隙巖體的連續-非連續變形以及含膠結的結構面組成塊體的局部失穩過程。選取甘肅北山某典型花崗巖研究區域測量的結構面數據以及搜索出的多種塊體，運用有限元軟件ABAQUS中的黏聚力模型(cohesive zone model，CZM)模擬具有填充和膠結的結構面的抗拉強度和黏聚強度。根據測量的結構面數據信息，分4種方案對膠結結構面的抗拉強度和黏聚強度進行賦值；運用Matlab程序對隧道洞室模型的inp文件進行修改，從而可以對洞室開挖邊界施加相應的節點荷載，通過對反加于圍巖邊界荷載的逐漸釋放來分析初始地應力和開挖誘導的二次地應力對塊體穩定的影響。結合以上幾點，綜合考慮初始地應力、開挖誘導的二次地應力、結構面的黏聚強度和抗拉強度，以及它們之間的摩擦應力等因素來研究塊體的穩定性。

1 黏聚力模型

(a) 法向

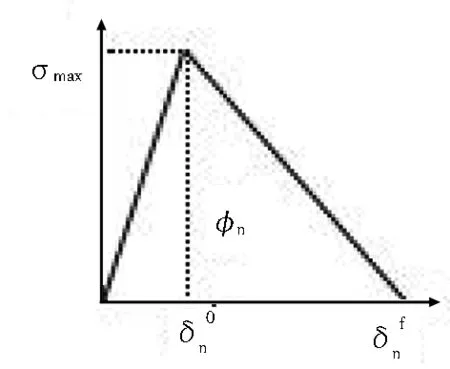
(b) 切向圖1 雙線性張力-位移關系Fig. 1 Bi-linear tension-displacement relationship

1.1 黏聚力單元損傷原理

在黏聚力單元損傷之前，認為其應力應變關系符合線彈性準則，如式(1)所示。2個相鄰單元之間用類似膠材料的黏聚力單元連接，該黏聚力單元很薄，有時考慮到實際的工程問題，黏聚力單元厚度常常設置成0。

(1)

式中：t為單元應變矢量；tn、ts、tt分別為單元法向和2個切向的牽引力；K為單元剛度矩陣；ε為應變矢量；εn、εs、εt分別為單元法向和2個切向的應變。

矢量ε表達式如下：

εn=dn/To,εs=ds/To,εt=dt/To

。

(2)

式中：dn、ds、dt分別為單元法向和2個切向變形黏聚力單元分開的距離；To為黏聚力單元最初的厚度。

利用名義應力比的二次交互函數準則來確定膠結結構面是否會斷裂，當臨界應力比平方和等于1時，認為損傷完全。此準則用公式表達如下[9]：

(3)

1.2 損傷模式

研究表明，裂紋的擴展是一個復合型損傷演化過程，包括法向和2個切向的擴展。B-K準則[10]被廣泛應用于預測裂縫擴展，其表達式見式(4)。該式用于當巖體完全沿第1、2剪切方向變形時，2個方向的臨界斷裂能相同的情況。

(4)

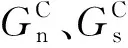
1.3 損傷演化

模擬材料的斷裂損傷演化通常采用剛度退化準則，該準則表達式如下[11]：

(5)

(6)

零厚度的黏聚力單元模型如圖2所示。圖中的中間層表示具有零厚度的黏聚力單元層，當塊體受到外力作用時，中間的黏聚力層會逐漸損傷；當其應力或應變滿足定義的初始臨界損傷準則時，則開始退化，黏聚力單元逐漸刪除，單元間的黏聚力消失，而上下面之間的摩擦力從分析步開始只要面面接觸就會一直起作用。根據摩爾-庫侖理論，黏聚力單元層的強度τ=c+σtanφ，其中c為結構面的黏聚力強度，σtanφ為結構面之間的摩擦強度。

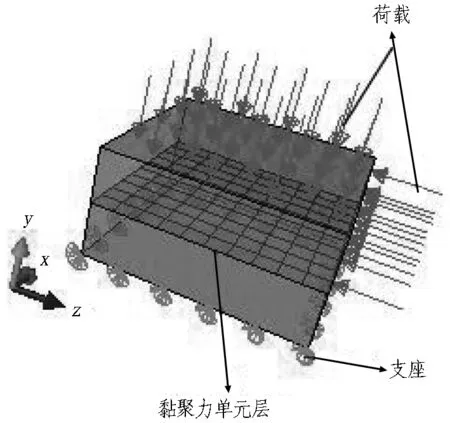
圖2 零厚度的黏聚力單元模型Fig. 2 Cohesive element model of zero thickness

2 圍巖塊體的穩定性分析

在甘肅北山某花崗巖典型區域研究范圍內進行塊體的搜索，得到的塊體如圖3所示。其中，1、2、4號塊體是四面體，3號塊體是五面體，且由幾何位置初步判斷，1、2、3號塊體可能出現失穩情況，4號塊體是穩定塊體。

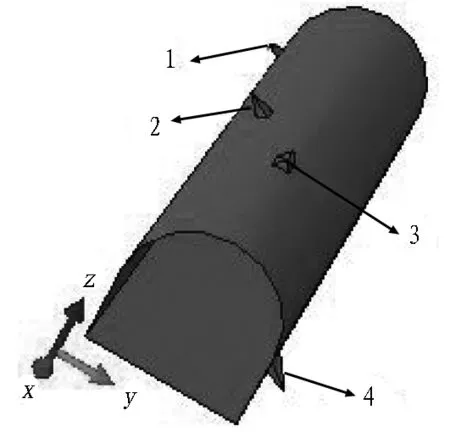
1—4表示塊體編號。

圖3搜索出的塊體示意圖
Fig. 3 Sketch of searched blocks

2.1 模型建立

根據得到的塊體結構面數據，以花崗巖典型區域地下開挖隧道為例，對開挖范圍內搜索出的塊體的穩定性進行研究。開挖隧道斷面由邊墻與拱頂組成，可以分別定義為直線段和圓弧段。考慮到模擬隧道開挖僅對一定范圍內的巖體產生影響，根據工程經驗，模型邊界距開挖洞口邊的距離超過5倍洞口直徑時，開挖產生的影響就會變得很小。在本次模擬中，考慮到洞口直徑為5 m左右，模型尺寸可取為40 m×60 m×60 m (長×寬×高)。根據北山巖體條件及核廢料地下處置的基本要求，計算模型上表面位于地下600 m埋深處，同時上表面的豎向應力按實測應力取值； 下表面位于660 m埋深處。模型的邊界條件為： 上邊界為自由邊界，下邊界約束豎向(z向)位移，左右邊界為側向約束。單元網格的尺寸從模型邊界到孔洞壁附近逐漸被細化，如圖4所示。

圖4 隧道模型的網格劃分Fig. 4 Meshing of tunnel model

2.2 材料及結構面參數

模型頂部為應力邊界條件，應力值為上覆巖石的質量，依據趙宏剛等[12]得出的巖石埋深與地應力的關系，取垂直主應力為16.2 MPa，x方向的側壓力系數為0.92，y方向的側壓力系數為0.65。根據北山某典型花崗巖采石場地區的統計資料，分別取表1所示的巖體物理力學參數，按照等效連續介質進行計算。

表1 巖體的物理力學參數Table 1 Physico-mechanical parameters of rock mass

結構面的強度包含抗剪強度和抗拉強度2部分，結合搜索出塊體的結構面特征以及相應的資料[13]，參照GB/T 50218—2014《工程巖體分級標準》[14]，得出其抗拉強度在0～0.04 MPa，相應的黏聚強度在0～0.12 MPa，內摩擦角在19°～29°。

2.3 模型分析步

本次模擬分為2個分析步，每個分析步與時間步相對應。第1個分析步是初始地應力平衡，時間步是0～0.1； 第2個分析步是模擬隧道開挖，時間步是0.1～1.4。為了分析開挖誘導的二次地應力的影響，把初始平衡步得到的開挖邊界應力加到隧道邊界上，如圖5所示。隨著時間步的增加，開挖邊界的節點力逐漸釋放，當時間步增加到1時，節點力釋放完成。釋放過程中，由于中間巖體被挖出，原有的地應力平衡被打破，將由此產生應力二次重分布； 同時，原有的結構面與新產生的臨空面形成關鍵塊體，在地應力以及自身重力的作用下，此塊體可能會出現失穩。

圖5 隧道邊界節點力Fig. 5 Joint force of tunnel boundary

2.4 模擬結果

考慮到不同位置的塊體可能的失穩情況，分4種方案進行模擬,具體參數見表2。整個方案中，4號塊體始終保持穩定。為了僅考慮摩擦力的影響，方案1把抗拉強度和黏聚強度賦予一個很小的數值(1×10-9MPa)，相應的摩擦因數見表2； 方案2、3、4分別考慮不同位置塊體可能的失穩情況，通過調整不同塊體結構面的抗拉強度和黏聚強度，確定影響塊體穩定的主要因素。

表2 塊體結構面參數的4種方案Table 2 Four schemes of block structural surface parameters

1)方案1模型不同時間步的位移云圖如圖6所示。在抗拉強度和黏聚強度接近于0，僅摩擦應力起作用的情況下，1、2、3號塊體幾乎同時掉落。圖7示出開挖時間步為0.1～1.4時的摩擦應力變化情況。由圖7可知，摩擦應力在起始階段逐漸增大，達到峰值后逐漸降低并趨于0。對應圖6來看，趨于0即塊體已經完全脫離巖體結構面并向下滑落，頂部3號塊體大約在時間步為0.5時最先脫離，另外2個塊體大約在時間步為0.6時脫離。2號塊體的摩擦應力始終相對較小，因此若想讓2號塊體保持穩定，提高塊體結構面的抗拉強度是最有效的辦法。對于3號塊體，由于其位置的特殊性而最容易失穩，在接下來的探討中，發現即使賦予該結構面參數區間內最大的抗拉強度、黏聚強度和摩擦因數，該塊體還是無法保持穩定。

2)方案2模型的位移云圖如圖8所示。由圖8可知： 開挖時間步為0.1時，3號塊體已經失穩，而2號塊體此時還處于穩定狀態； 隨著開挖進行，二次應力逐漸釋放，在時間步為1時，應力釋放完成，2號塊體已經失穩，1號塊體始終保持穩定狀態，塊體的位移曲線如圖9所示。下面主要探討3號塊體結構面的損傷情況，黏聚力單元的損傷情況如圖10所示。圖10(a)示出時間步為0.1時，3號塊體的結構面接近損傷完全(時間步為1時損傷破壞)，黏聚力單元的底邊邊角損傷最為嚴重； 時間步為0.3時，底邊邊角和兩側面部分已經完全損傷，并失效刪除； 時間步為0.4時，已經完全失效刪除。

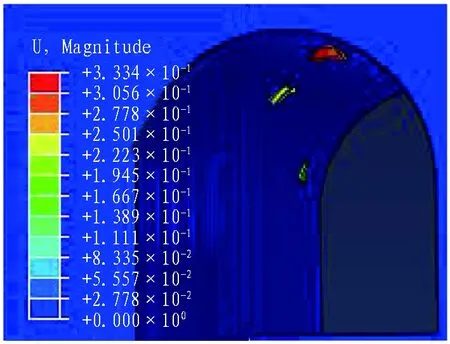
(a) 時間步為0.3

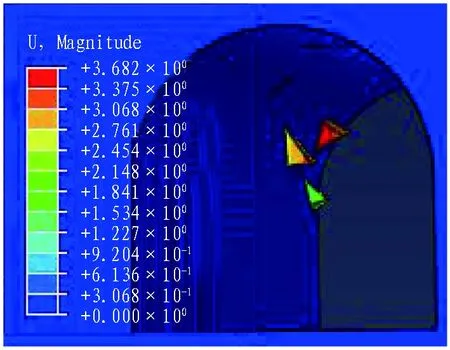
(b) 時間步為1圖6 方案1不同時間步的位移云圖(單位： m)Fig. 6 Displacement nephograms of block with different time steps in scheme 1 (unit: m)

圖7 方案1不同塊體的摩擦應力的時間步曲線Fig. 7 Curves of relationship between time steps and friction stresses of different blocks in scheme 1

(a) 時間步為0.1

(b) 時間步為1圖8 方案2不同時間步的位移云圖(單位： m)Fig. 8 Displacement nephograms of block with different time steps in scheme 2 (unit: m)

圖9 方案2塊體位移隨時間步的變化情況Fig. 9 Curves of relationship between time steps and friction stresses of different blocks in scheme 2

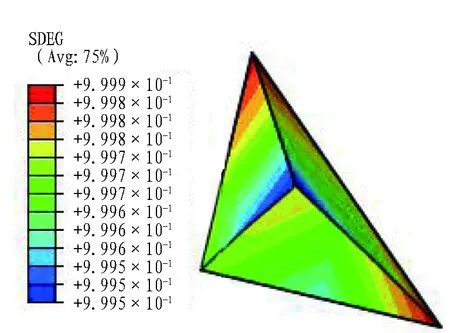
3)方案3模型的位移云圖如圖11所示。由圖11可知: 降低1號塊體結構面的摩擦因數而黏聚力不變，塊體在時間步為1時出現失穩并逐漸滑落，此時由于2號塊體結構面的黏聚力增加到0.1 MPa，摩擦因數為0.45，整個分析步過程中，2號塊體都保持穩定； 3號塊體此時已被賦予結構面參數區間的最大抗拉強度、黏聚強度和摩擦因數，但依然失穩。方案3塊體位移曲線如圖12所示，1號塊體結構面的損傷情況如圖13所示。

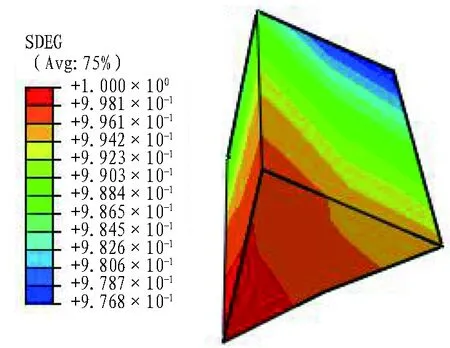
(a) 時間步為0.1

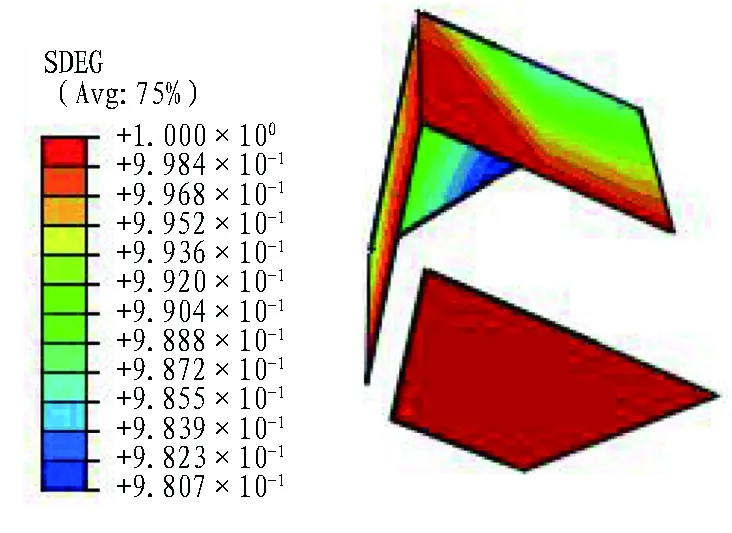
(b) 時間步為0.3圖10 3號塊體結構面隨時間步變化的損傷情況Fig. 10 Damage of structural surfaces of block 3 variating with time steps

(a) 時間步為0.3

(b) 時間步為1圖11 方案3不同時間步的位移云圖(單位： m)Fig. 11 Displacement nephograms of block with different time steps in scheme 3 (unit: m)

4)方案4位移云圖如14所示。把2號塊體結構面的摩擦因數降到最小值0.34，此時黏聚力沒有變，2號塊體在時間步為0.8時出現失穩，到時間步為1時出現明顯的滑落情況。值得注意的是，計算過程中1號塊體結構面的摩擦因數由方案3的0.4提高到0.42，而此時的1號塊體卻比方案3滑落的早。由此可見，塊體間的滑落是相互影響的，一個塊體的滑落勢必會影響其他塊體。方案4塊體的位移曲線如圖15所示。

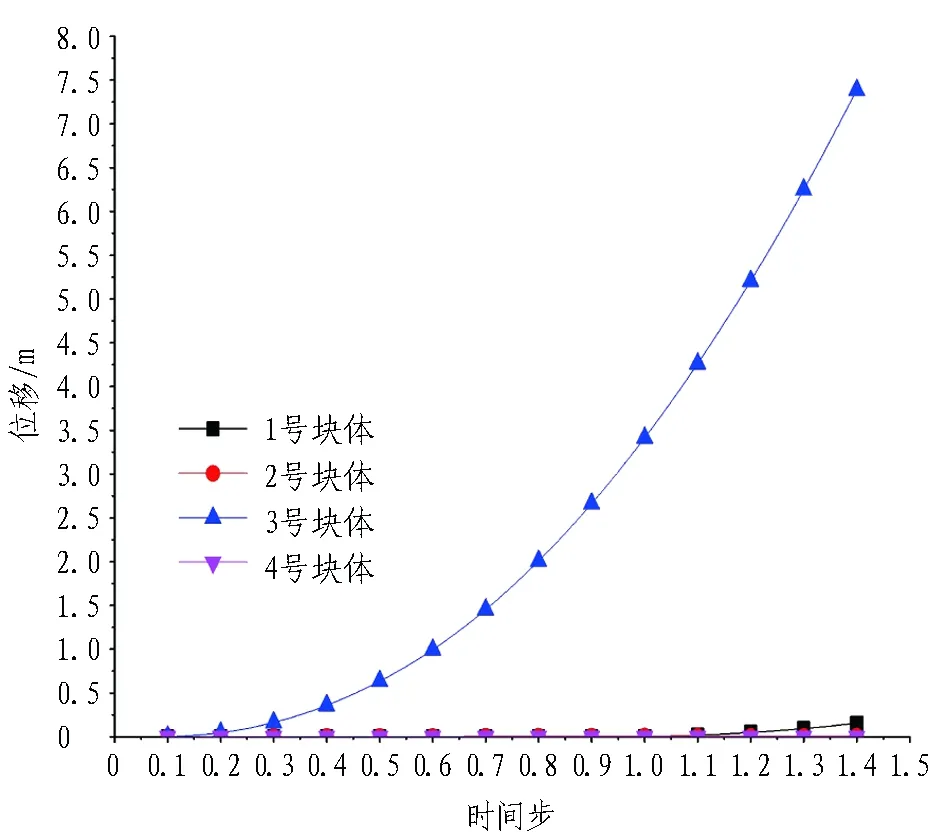
圖12 方案3塊體位移隨時間步的變化情況Fig. 12 Curves of relationship between time steps and friction stresses of different blocks in scheme 3

(a) 時間步為0.3

(b) 時間步為0.9圖13 1號塊體結構面隨時間步變化的損傷情況Fig. 13 Damage of structural surfaces of block 1 variating with time steps

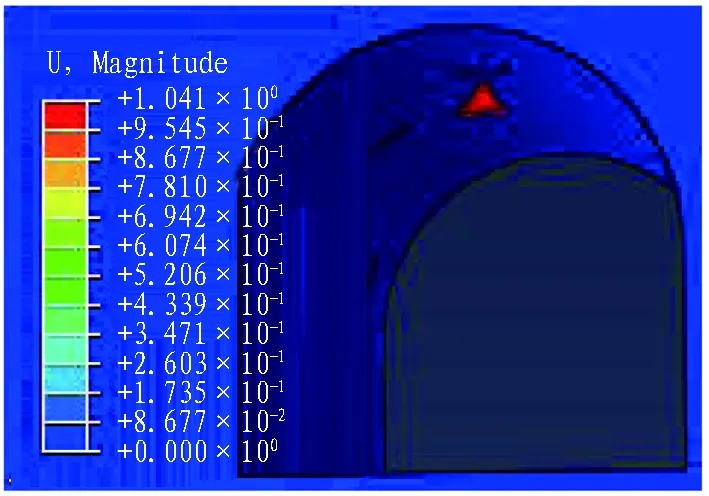
(a) 時間步為0.5

(b) 時間步為1圖14 方案4不同時間步的位移云圖(單位： m)Fig. 14 Displacement nephograms of block with different time steps in scheme 4 (unit: m)

圖15 方案4塊體位移隨時間步的變化情況Fig. 15 Curves of relationship between time steps and friction stresses of different blocks in scheme 4

3 結論與討論

本文運用黏聚力模型，結合甘肅北山某花崗巖典型區域搜索出的塊體，通過考慮具有填充和膠結的結構面的抗拉強度、黏聚強度以及摩擦應力等因素，分析不同位置塊體的穩定情況。得到主要結論如下。

1)采用黏聚力單元不僅能模擬僅有摩擦應力作用的結構面情況，還能較好地模擬具有填充和膠結的結構面的抗拉強度和黏聚強度，以及結構面的滑移和脫開行為，可作為塊體穩定分析計算的工具。

2)實際隧道開挖過程中，頂部的塊體最容易失穩，因此在為隧道設計襯砌時應適當加強襯砌頂部的強度。此外，抗拉強度、黏聚強度和摩擦應力共同構成了結構面的強度，不同位置的塊體滑落是相互影響的，一個塊體的滑落勢必會影響其他塊體的穩定性。

3)采用黏聚力單元模擬膠結結構面的抗拉強度和黏聚強度，通過把初始平衡步得到的開挖邊界應力反加到隧道邊界上，并在開挖步逐漸釋放邊界應力，從而可以表征出黏聚力單元隨二次地應力釋放而逐漸損傷的過程，這為模擬結構面損傷隨時間的漸進性發展提供了一個新思路。

本文的研究尚有許多不足之處，使用的黏聚力損傷模型為常用的雙線性函數，與實際膠結結構面隨外力具體損傷的契合度也有待改進。此外，模擬含有巖橋的塊體穩定也是以后研究的重點與難點。