不確定信息下的應(yīng)急物流系統(tǒng)定位-路徑問題研究

王純

摘要：針對突發(fā)公共衛(wèi)生事件之后的應(yīng)急物流系統(tǒng)，以總成本最小為目標(biāo)建立了不確定機會約束模型。考慮到實際情況，假設(shè)應(yīng)急物資必須在需求點的限制期內(nèi)到達(dá)以及車輛與候選配送中心的容量是有限的，并且認(rèn)為需求點的需求量是不確定的，但是兩節(jié)點的運輸時間是確定的。同時為了節(jié)約成本，還假設(shè)車輛在完成配送任務(wù)后就近停靠在已開設(shè)的配送中心。進(jìn)一步，應(yīng)用遺傳算法對該模型進(jìn)行求解，最終給出算例來說明模型以及算法的可用性。

Abstract： For the emergency logistics system after public health emergency， an uncertain opportunity constraint model is established with the goal of minimum total cost. Considering the actual situation， it is assumed that the emergency supplies must arrive before the restriction period of the demand point and the capacity of the vehicle and the candidate distribution center is limited， and the material demand of the demand point is considered to be uncertain， but the transportation time of the two nodes is determined. At the same time， in order to save costs， it is also assumed that the vehicle will stop at the already opened distribution center after completing its own distribution task. Furthermore， the genetic algorithm is applied to solve the model， and an example is given to prove the validity of the model and the algorithm.

關(guān)鍵詞：突發(fā)公共衛(wèi)生事件;應(yīng)急物流;定位-路徑問題;不確定變量;優(yōu)化建模

Key words： public health emergency;emergency logistics;locating-routing problem;uncertain variable;optimization modeling

中圖分類號：F252? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻(xiàn)標(biāo)識碼：A? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文章編號：1006-4311（2019）36-0154-04

0? 引言

公共衛(wèi)生事件的頻頻發(fā)生對人民的生命財產(chǎn)安全造成了嚴(yán)重的威脅。例如2003年SARS病毒、2004年劣質(zhì)奶粉事件以及2005年的禽流感等等。據(jù)統(tǒng)計，2003年SARS病毒給我國造成了高達(dá)176億美元的經(jīng)濟(jì)損失。突發(fā)公共衛(wèi)生事件不僅會造成巨大的經(jīng)濟(jì)損失，而且還會引發(fā)公眾的恐懼、焦慮等情緒，這種情緒將會對公眾的心理產(chǎn)生嚴(yán)重的危害，進(jìn)而將產(chǎn)生嚴(yán)重的政治以及社會影響。在突發(fā)公共衛(wèi)生事件后的應(yīng)急物流系統(tǒng)中有兩個關(guān)鍵問題需要得到及時地解決：第一個是應(yīng)急設(shè)施如何定位，即應(yīng)急設(shè)施定位-分配問題（Location-allocation Problem，LAP）;第二個是應(yīng)急救援車輛路徑如何規(guī)劃，即車輛路徑問題（Vehicle Routing Problem，VRP）。這兩個問題是相互影響的，需要對其進(jìn)行集成優(yōu)化，即研究突發(fā)公共衛(wèi)生事件后應(yīng)急物流系統(tǒng)中的定位-路徑問題（Location-routing Problem，LRP）。因此，國內(nèi)外學(xué)者開始從不同的角度研究應(yīng)急物流系統(tǒng)的LRP問題。

在經(jīng)典規(guī)劃中，Yi和？魻zdamarb[1]協(xié)調(diào)優(yōu)化了應(yīng)急物資配送和傷員運送救治問題，建立了混合整數(shù)物資網(wǎng)絡(luò)流模型。其中，每輛配送車輛被當(dāng)成一個整體貨物來看待，是整數(shù)變量，而不是0-1變量。Ahmadi等[2]以總時間最短和總費用最小為目標(biāo)建立了混合非線性應(yīng)急LRP優(yōu)化模型。樓振凱[3]以應(yīng)急物流系統(tǒng)總時間最小為上層目標(biāo)，配送成本和時間懲罰成本之和最小為下層目標(biāo)，建立了雙層應(yīng)急LRP優(yōu)化模型。

在隨機規(guī)劃中，Laporte等[4]建立了兩階段應(yīng)急LRP優(yōu)化模型，第一階段在不知道實際供應(yīng)的情況下確定倉庫位置、車隊規(guī)模以及計劃路線，第二階段在供給量已知條件下修訂車輛路徑。代穎和馬祖軍[5]假設(shè)應(yīng)急物資需求和救援車輛運輸時間都是隨機的，基于機會約束規(guī)劃方法，以系統(tǒng)總成本最小為目標(biāo)建立了帶時間窗的應(yīng)急LRP優(yōu)化模型。孫華麗等[6]以總救援時間最短和系統(tǒng)總成本最小為目標(biāo)，建立了應(yīng)急LRP優(yōu)化模型。

在應(yīng)用概率論時，通常假設(shè)估計的累計概率分布與頻率足夠接近。若要得到累計概率分布函數(shù)，這意味著需要進(jìn)行多次獨立重復(fù)性實驗來獲得大量的觀測數(shù)據(jù)。但是由于技術(shù)和經(jīng)濟(jì)等原因，無法獲得樣本，例如無法獲得正在使用的橋梁的承重量。因此，在評估某件可能發(fā)生的事件的可能性時必須依賴專家給出的信度。但是，根據(jù)諾貝爾經(jīng)濟(jì)學(xué)獎得主Kahneman和Tversky[7]的觀點，人們經(jīng)常會高估不太可能發(fā)生的事件;Liu[8]也指出人類的估計值總是比真實值范圍大得多，這意味著專家信度與真實的頻率存在著很大的差距。在這種情況下，如果我們采用概率論處理的話，可能會出現(xiàn)違反人類直覺的結(jié)果[9]。這就需要尋找一種新的數(shù)學(xué)工具來處理專家的信度。

為了處理專家的信度，Liu[10]在2007年基于規(guī)范性、對偶性、次可加性公理引入了不確定理論。到目前為止，不確定理論已經(jīng)成為一個幾乎完整的數(shù)學(xué)系統(tǒng)。有學(xué)者將不確定理論運用到了應(yīng)急物流系統(tǒng)優(yōu)化中，Zhang等[11]假設(shè)兩節(jié)點之間的距離、受害點的需求量以及應(yīng)急服務(wù)設(shè)施的建設(shè)成本均為不確定變量，利用機會約束建立了單目標(biāo)不確定應(yīng)急LRP優(yōu)化模型，但是考慮是車輛閉環(huán)的情況，即車輛在完成自身配送任務(wù)之后必須回到出發(fā)的配送中心，從而解決了閉環(huán)應(yīng)急LRP優(yōu)化問題。

1? 基礎(chǔ)理論

定義1[10]? 假設(shè)？祝是一個非空集合，A是？祝上的？滓-代數(shù)，則A中的元素？撰稱為事件。如果M是從A到[0，1]的集函數(shù)，且M滿足以下公理：

公理1. （規(guī)范性公理）對全集？祝，有M{？祝}=1;

公理2. （對偶性公理）對任意的事件？撰，有M{？撰}+M{？撰c}=1;

公理3. （次可加性公理）對A中任意可數(shù)的事件序列

公理4. （乘積公理）假設(shè)（？祝k，Ak，Mk）是不確定空間，其中k=1，2，…。若對Ak中任意的？撰k（k=1，2，…），有

M則稱M為乘積不確定測度。

定義2[10]? 假設(shè)函數(shù)？孜是從不確定空間（？祝，A，M）映射到實數(shù)集上的可測函數(shù)，即對任意的實數(shù)Borel集B，集合是一個事件，則稱？孜是不確定變量。

定義3[10] 假設(shè)？孜是不確定變量，對任意的實數(shù)x，則稱函數(shù)？椎（x）=M? {？孜？燮x}為？孜的不確定分布。

定義4[10]? 若不確定分布？椎（x）是關(guān)于x的連續(xù)的嚴(yán)格單增函數(shù)，其中，且滿足和，則稱？椎（x）是正則的。若？椎（x）是？孜的正則不確定分布，則它的逆函數(shù)稱為？孜的逆不確定

分布。

定義5[12]? 對任意的實數(shù)Borel集B1，B2，…，Bn，若成立，則稱不確定變量是？孜1，？孜2，…，？孜n相互獨立的。

定義6[10]? 假設(shè)？孜是不確定變量，則稱為？孜的期望，其中以上兩個積分至少有一個是有限的。

定理1[12] 假設(shè)？孜1，？孜2，…，？孜n是獨立的不確定變量，f1，f2，…，fn是可測的實函數(shù)，則f1（？孜1），f2（？孜2），…，fn（？孜n）是獨立的不確定變量。

定理2[10] 假設(shè)？孜1，？孜2，…，？孜n是不確定變量，f是可測的實函數(shù)，則是不確定變量。

定理3[10] 假設(shè)？孜1，？孜2，…，？孜n是獨立的不確定變量，且分別對應(yīng)有正則不確定分布。若關(guān)于？孜1，？孜2，…，？孜m嚴(yán)格單調(diào)遞增，且關(guān)于嚴(yán)格單調(diào)遞減，則不確定變量=的逆不確定分布為

2? 模型構(gòu)建

2.1 問題描述

當(dāng)SARS病毒、禽流感等公共衛(wèi)生事件發(fā)生的時候，必須在一定的時間內(nèi)將救援物資送到醫(yī)院，否則就會耽誤治療，錯過最佳的治療時機。由于疾病的蔓延性或者有未發(fā)現(xiàn)的感染者，需要治療的人員數(shù)量是不能完全確定的，所以當(dāng)突發(fā)公共衛(wèi)生事件發(fā)生時的物資需求是不確定的，假設(shè)為不確定變量，并且假設(shè)任意兩個應(yīng)急物資需求點的需求量是獨立的。但是在突發(fā)公共衛(wèi)生事件不會造成道路的破壞，所以兩節(jié)點之間的運輸時間是確定的。抽象出LRP問題：假設(shè)有一組有容量限制的候選應(yīng)急物流配送中心;還有一組應(yīng)急物資需求點，每個需求點的需求量是不確定的，假設(shè)為一個不確定變量，并且假設(shè)任意兩個應(yīng)急物資需求點的需求量是獨立的。每個物資需求點都有一個限制期，要求應(yīng)急物資必須在需求點的限制期之前到達(dá);另外還有若干輛不同型號且均有容量限制的車輛，車輛在兩節(jié)點之間的運輸時間是確定的，并且車輛在完成自身的配送任務(wù)后，就近停靠在已開放的配送中心。

2.2 模型建立

式（1）是模型的總成本最小的目標(biāo)，其中總成本包括配送中心的建設(shè)成本、車輛的固定成本以及車輛隨運輸距離得增加而增加的運輸成本;式（2）表示車輛的容量約束;式（3）表示配送中心的容量約束;式（4）為Tbk的表達(dá)式;式（5）表示兩個配送中心之間沒有直接路徑相連;式（6）表示集合D中的每一個需求點有且只有一輛車為其服務(wù);式（7）表示開設(shè)的配送中心必須發(fā)車;式（8）表示未開設(shè)的配送中心不能發(fā)車;式（9）表示未開設(shè)的配送中心沒有車輛到達(dá);式（10）表示需求點的限制期要求;式（11）表示車輛只分配給已開設(shè)的配送中心;式（12）表示每輛車在完成相應(yīng)的配送任務(wù)后，必須選擇一個配送中心停靠。

式（2）等價于

式（3）等價于

3? 算法設(shè)計與算例求解

3.1 算法設(shè)計

3.1.1 染色體編碼

在本問題中，根據(jù)解的特點，我們采用的是自然數(shù)編碼。每條染色體由三個子串構(gòu)成，子串一有n個基因位，每個基因位的值均從1-K的自然數(shù)中隨機選取，表示D中的需求點對應(yīng)的配送車輛。子串二的長度為n，每個基因位的取值在1-n的自然數(shù)隨機排列生成，表示路線當(dāng)中的需求點排列的順序。子串三的長度為m，每個基因位的取值在n+1-n+m的自然數(shù)中隨機生成表示每輛車被分配到的配送中心的標(biāo)號。

3.1.2 約束條件處理

本文利用罰函數(shù)的思想來對約束進(jìn)行處理。對于車輛容量約束式（14），令，則車輛容量約束式（16）等價于，所以在目標(biāo)函數(shù)中加入一項：，其中N1是個很大的數(shù)。同理，對于配送中心容量約束式（15），在目標(biāo)函數(shù)中加入一項：，其中N2是個很大的數(shù)。再同理，對于需求點的限制期約束式（10），在目標(biāo)函數(shù)中加入一項：，其中N3是個很大的數(shù)。

3.1.3 適應(yīng)度函數(shù)

此時，目標(biāo)函數(shù)為

由于目標(biāo)函數(shù)為，所以適應(yīng)度函數(shù)取，從而使得目標(biāo)值越小的染色體具有越大的適應(yīng)度。

3.2 算例分析

假設(shè)有10個需求點，編號為1-10;有3個配送中心，編號為11-13;有3輛不同型號的車。配送中心的參數(shù)如表1所示，各需求點的需求量服從如表2所示的線性不確定分布，配送車輛的參數(shù)如表3所示，各節(jié)點之間的運輸時間服從如表4所示。

本文使用MATLAB軟件編程，設(shè)置迭代次數(shù)為300代，初始種群為40，交叉概率Pc=0.8，變異概率Pm=0.1，預(yù)設(shè)的置信水平？茁1=？茁2=0.95。程序運行了50次，均是選擇配送中心11、12和13，得到的最優(yōu)成本為25135元。得到的選址-路徑結(jié)果如表5所示，對應(yīng)的目標(biāo)值隨迭代次數(shù)的收斂圖如圖1所示。

從表5可得，從候選配送中心中選擇了11、12和13，有3輛車參與運輸，車輛3屬于配送中心11，車輛1屬于配送中心12，車輛2屬于配送中心13。同時得出每輛車服務(wù)需求點的順序，3條配送路徑分別為：車輛1為12-7-6-10-13;車輛2為13-1-2-4-13;車輛3為11-5-8-3-9-11。

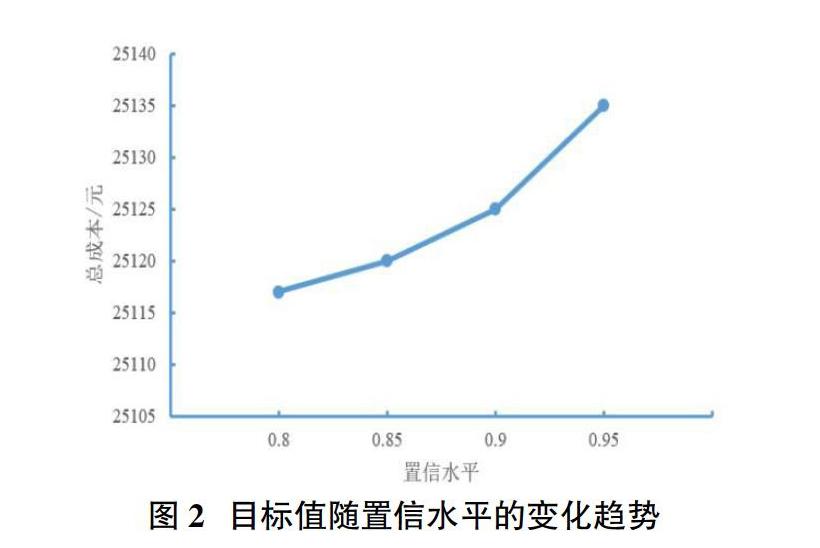
從目標(biāo)值的收斂圖（圖1）也可以看出，目標(biāo)收斂很快，在50多代即可求得最優(yōu)解，能滿足模型的求解要求。此時，改變模型中置信水平，運算結(jié)果也會不同。目標(biāo)函數(shù)值隨置信水平的變化趨勢如圖2所示。

由圖2可得，隨著置信水平的提高，系統(tǒng)的應(yīng)急物流成本是升高的。當(dāng)物資需求量滿足配送中心容量以及車輛容量的置信水平越低，選出的配送中心數(shù)量以及車輛數(shù)量可能會越少，則得到的系統(tǒng)應(yīng)急總成本越小;而置信水平越高，為了能及時地送達(dá)物資，會選擇容量更大的車輛或配送中心，或者是選擇更多的配送中心和車輛導(dǎo)致系統(tǒng)總的應(yīng)急成本升高。

4? 結(jié)語

本文考慮了在突發(fā)公共衛(wèi)生事件后應(yīng)急物流系統(tǒng)的定位-路徑問題，建立了一個總成本最小的不確定優(yōu)化模型。在以后的研究工作中，可以考慮車輛的多次往返配送以及需求點的需求量可能超過車輛容量的情況，甚至可以考慮多式聯(lián)運運輸應(yīng)急物資的情況。

參考文獻(xiàn)：

[1]Yi W， ？魻zdamarb L. A Dynamic Logistics Coordination Model for Evacuation and Support in Disaster Response Activities[J]. European Journal of Operational Research， 2007， 179（3）： 1177-1193.

[2]Ahmadi M， Seifi A， Tootooni B. A Humanitarian Logistics Model for Disaster Relief Operation Considering Network Failure and Standard Relief Time： A Case Study on San Francisco District[J]. Transportation Research Part E， 2015， 75（1）： 145-163.

[3]樓振凱.應(yīng)急物流系統(tǒng) LRP 的雙層優(yōu)化模型及算法[J].中國管理科學(xué)，2017，25（11）：151-157.

[4]Laporte G， Louveaux F， Mercure H. Models and Exact Solutions for a Class of Stochastic Locationrouting Problems[J]. European Journal of Operational Research， 1989， 39（1）： 71-78.

[5]代穎，馬祖軍.應(yīng)急物流系統(tǒng)中的隨機定位-路徑問題[J]. 系統(tǒng)管理學(xué)報，2012，1（2）：212-217，223.

[6]孫華麗，王循慶，薛耀鋒.隨機需求應(yīng)急物流多階段定位-路徑魯棒優(yōu)化研究[J].運籌與管理，2013（6）：45-51.

[7]Kahneman D， Tversky A. Prospect Theory： An Analysis of Decisions under Risk[J]. Econometrica， 1979， 47： 263-291.

[8]Liu B. Uncertainty Theory[M]. 4nd ed.， Berlin： Springer-Verlag， 2015.

[9]Liu B. Why is There a Need for Uncertainty Theory？[J]. Journal of Uncertain Systems， 2012， 6（1）： 3-10.

[10]Liu B. Uncertainty Theory[M]. 2nd ed.， Berlin： Springer-Verlag， 2007.

[11]Liu B. Some Research Problems in Uncertainty Theory[J]. Journal of Uncertain Systems， 2009， 3（1）： 3-10.

[12]Zhang B， Li H， Li S， Peng J. Sustainable Multi-depot Emergency Facilities Location-routing Problem with Uncertain Information[J]. Applied Mathematics and Computation， 2018， 333： 506-520.