把握邏輯起點 找準現實起點 構建有效教學

胡昌敏

[摘要]數學課堂需要關注學生的學習起點，才能提高課堂實效。熟讀教材，有助于教師把握學習的邏輯起點;前測分析，有助于了解學生的實際情況，找準學生學習的現實起點。在此基礎上，教師才能展開富有成效的、針對性的教學實踐。從“多位數乘一位數口算乘法”的學習邏輯起點和現實起點進行全面、深入地分析，探索構建有效教學的策略。

[關鍵詞]邏輯起點;現實起點;起點差異;口算乘法

[中圖分類號]

G623.5

[文獻標識碼]A

[文章編號] 1007-9068（ 2019）35-0028-03

數學是一門邏輯性很強的學科，知識間的聯系極其緊密，層次性也很強。多數教師往往習慣做好自認為充分的準備去面對“毫不知情”的學生。如果對學生的現實起點認識和把握不夠，就會導致好生上課“吃不飽”、差生“消化不了”，教學的有效性毫無疑問會大打折扣。可見，數學教學應找準學生學習的起點，并鉆研教材的內在聯系，真正做到因材施教。那如何找準學生的學習起點呢？下面，我以自己在“鄉村學校共生發展聯合體”三校數學聯盟活動中執教的“多位數乘一位數口算乘法”為例，進行說明論述。

一、鉆研教材，把握學習的邏輯起點

邏輯起點是指學生按照教材的進度、課程標準的要求在學習某內容之前應該具有的知識和能力基礎。那么，如何才能把握好學生學習的邏輯起點呢？我認為這取決于兩個方面：一是教師本身的數學知識結構，二是教材的教學編排體系。因此要準確把握學生學習的邏輯起點，一靠教師本身扎實的數學素養，二靠教師認真鉆研教材，從整體的角度去考慮學生的數學學習。

“口算乘法”是人教版教材三年級上冊第六單元的內容，是在學生已經掌握表內乘法的基礎上進行學習的。教材在編排時安排了兩個例題：

例1：坐碰碰車每人20元，3人需要多少錢？

例2：坐過山車每人12元，3人需要多少錢？

通過鉆研教材，我發現學生學習“口算乘法”的邏輯起點是已經掌握了“表內乘法”，因而我注重學生已有的知識經驗，以表內乘法為基礎，逐步過渡到整十、整百數以及任意兩位數乘一位數的口算。在學習方法上，讓學生在已有知識的基礎上自主探索，用遷移類推的方法建構新知，進一步引導學生在新舊知識之間建立聯系，從而理解算理，掌握算法。

【第一次教學實踐及反思】

教學例1：坐碰碰車每人20元，3人需要多少錢？

（1）學生列出算式20x3，并說明20x3表示的意思。

（2）學生嘗試把20x3的計算方法寫在紙上。

（3）學生解答：因為20+20+20=60（或2x3=6），所以20x3=60。

（4）學生動手操作：擺小棒圖驗證20x3=60。

（ 5）鞏固練習：口算20x6和200x3，并說一說計算方法。

（6）小結算法。

（7）挑戰練習：500x8=？并追問，小結。

教學例2：坐過山車每人12元，3人需要多少錢？

（1）學生列出算式12x3，并說明12x3表示的意思。

（2）學生嘗試把12x3的計算方法寫在紙上。

（3）學生解答：因為12+12+12=36（或lOx3=30，2x3=6），所以12x3=36。

（4）學生動手操作：擺小棒圖驗證12x3=36。

（5）同桌互相說12x3的計算過程。

（6）鞏固練習：12x4、32x2、23x3。口算，并說一說它們的共同之處。

小結：都是把兩位數分成整十數和一位數，分別乘一位數算出積后再相加。

一節課下來，參加三校聯盟活動的近50位數學教師都認為這節課條理清楚，不僅解決了問題，而且每個教學環節落實到位，整節課學生參與度極高。學習方式多樣化，既有學生靜心動腦思考、嘗試計算的自主學習，又有動手操作擺小棒、小組探究的合作學習。課后練習的結果表明，大多數學生都已掌握新課內容，聽課教師認同我所把握的學生學習的邏輯起點，能夠從學生的已有知識（表內乘法）出發，練習設計呈階梯式上升，循序漸進，滿足不同學生的學習需求。但是，我心里總有一絲莫名的遺憾：課堂教學進程過于流暢，一點沖突都沒有，所有的知識學生都掌握得很好。但正是這看似“完美”的課堂卻抹殺了學生質疑的能力，我似乎還是課堂上那光芒四射的主角。那么一節課下來，學生到底有什么收獲呢？比如已知2x3=6，為什么就能推導出20x3等于60呢？學生到底知不知道算法背后的算理？還是學生只是記住了“末尾去0法”所帶來的算法的簡便性？學生是不是只“知其然，而不知其所以然”呢？這些困惑讓我忐忑不安，總覺得學生的收獲并不是來自本節課的學習，而是他們本來就知道的，那么對他們而言，可能是為了配合我演完了這40分鐘的“戲”，他們其實一無所獲。

本次教學失敗的主要根源在于教學時只一味地追求學習的邏輯起點，忽略了教材的本質特征，以致我以為的學生的邏輯起點并不是學生真正的現實起點。

二、前測分析，找準學習的現實起點

那學生真正的現實起點在哪呢？難道學生的現實起點不僅僅只停留在“表內乘法”嗎？課程標準指出：“教師教學應該以學生的認知發展水平和已有的經驗為基礎。”基于這一理念，我設計了“多位數乘一位數口算乘法”的兩道前測題，并對我校三年級3個班的116名學生進行了學習前測。

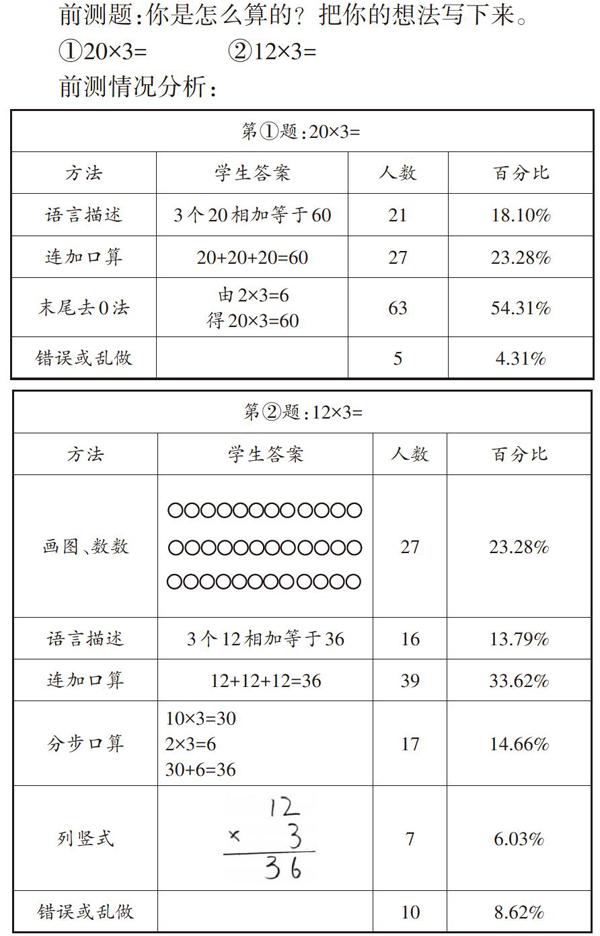
前測題：你是怎么算的？把你的想法寫下來。

①20x3=②12x3=

前測情況分析：

根據以往的學習經驗和知識發展水平，大多數學生能夠用畫圖、語言描述、口算等方法得出正確結果，第①題的正確率是95.69%，第②題的正確率是91.38%。這些數據表明，90%以上的學生在學習口算乘法之前已經掌握了整十、整百數乘一位數以及兩位數乘一位數（不進位）的計算方法，能夠通過不同的方法算出正確結果。也就是說，學生的現實起點不再僅僅停留在二年級的“表內乘法”，而是能夠靈活運用“表內乘法”和“萬以內數的組成”等知識和經驗來口算簡單的多位數乘一位數。如果在教學時把學生的起點只定在“表內乘法”這個邏輯起點上，顯然就太低了，不符合學生的現實起點，造成90%以上的學生“吃不飽”。

本學期.我還有幸參加了“千課萬人數學核心素養高級論壇”活動，其中有一節課正好是數學特級教師羅明亮執教的“多位數乘一位數口算乘法”。回校后，我結合羅明亮老師的教學理念，再根據我校學生的現實起點，進行了第二次教學實踐。

【第二次教學實踐及反思】

（1）談話引入乘法口訣，提問：為什么乘法口訣只編到97讓學生帶著思考進入新課學習。

（2）讓學生計算20x3，追問：乘法口訣沒有20x3，你是怎么算的？（引出口訣：二三得六）在計數器上畫一畫，表示出2x3和20x3，并說說區別。

（3）鞏固練習：計算200x3和2000x3，并說說發現。

（4）挑戰練習：500x8=？并追問：乘數500的末尾明明只有2個0，為什么積的末尾卻有3個07

（5）讓學生嘗試計算12x4、312x3，并請兩人到黑板上作答。提問：兩個算式的計算方法有什么共同點？學生回答：把大的數拆分后用口訣計算，再把積相加。

（6）結合小棒圖，同桌互相說12x4的計算過程。

（7）回顧問題：乘法口訣為什么只編到97

（8）鞏固練習（略）。

（9）拓展練習：只用“二四得八”這句口訣，猜一猜信封里裝的是什么算式？根據學生的回答依次出示：40x2、22x4、0.444x2。

第二次教學實踐中，學生的思維能夠產生碰撞，學生不再只是配合我“演戲”，人人參與其中。尤其是“為什么乘法口訣只編到9”這個問題，讓學生感到丈二和尚摸不著頭腦。有的學生說不是口訣沒有了，而是以后再學下去口訣會繼續編下去的，基礎好的學生覺得口訣編到9就夠了，因為生活中他從來沒有聽說過比9還大的乘法口訣，可是到底為什么口訣只編到9，學生卻說不出個所以然。

而通過本節課的學習之后，大多數的學生能夠體會到口訣為什么只編到9就沒有了，是因為即使再大的數也可以拆分成表內乘法來計算。同樣，在教學多位數乘一位數（不進位）口算乘法的過程中，如果像第一次教學那樣只計算兩位數乘一位數，學生就會覺得沒有挑戰性，求知欲就不會那么強烈。如果讓學生一次性計算兩位數、三位數甚至四位數乘一位數，那他們心中憋著的那股勁就能完全釋放出來。最后一題的拓展練習更能把基礎好的學生的思維創造力激發出來，從40x2到22x4，再到0.444x2，學生的認知不斷受到沖擊，到了課堂結束時學生還覺得意猶未盡。

第二次教學實踐正因為我基于教材的邏輯起點，又從學生的現實起點出發，做到著眼于學生思維長遠發展的教學有效性，相較于上次教學，師生都收獲頗豐，

三、關注差異，構建有效的課堂教學

（一）尊重學生，關注起點差異

由于現實條件、環境的不同，即使是同年級的學生，因生活在不同的地區、不同的家庭，不同的學校、不同的班級，學習的現實起點也會有很大的差異。我們所教的每一屆學生，情況都不盡相同，甚至差別很大，教學時要找出不同學生的現實起點，做到心中有數，進而進行有針對性的課堂教學。這種目的明確、精準把握學生學習起點的課堂，才能讓不同水平的學生都能真正學有所得。課程標準所提出的“促進不同的學生在數學上得到不同的發展”的目標也就有了保障。

（二）找準起點，構建有效教學

在平時教學中，我們要關注邏輯起點和現實起點的差異，運用策略化解差異，構建有效的課堂教學。

1.新舊連接：現實起點相當于邏輯起點

在這種情況下，學生學習此內容前實際應該具有的基礎知識、基本技能和基本活動經驗與教材的邏輯起點基本保持一致。此時，教師需要找到新舊知識的連接點，在此基礎上進行有效教學。

2.取長補短：現實起點高于邏輯起點

在這種情況下，有些學生通過自身預習、校外補習或者通過網絡學習，學習此內容前實際所具有的現實起點已經高于教材所要求的邏輯起點。教學中，學生現實起點高于邏輯起點的現象時有發生，尤其是借班上課的公開課中，碰到這種情況，大多數學生只是配合教師“演戲”而已。

3.因材施教：現實起點低于邏輯起點

艾賓浩斯遺忘曲線告訴我們，隨著時間的推移，人是會遺忘的，學生遺忘的程度和速度因人而異，各不相同。這時，就會出現“現實起點低于邏輯起點”的現象，這就要求教師在教學設計時需要喚醒學生的學習經驗。

（三）多種渠道，尋找有效路徑

《義務教育數學課程標準（2011年版）》指出：“數學教學應該以學生的認知發展水平和已有的經驗為基礎，面向全體學生，注重啟發和因材施教。”在課前，教師對教材的邏輯起點和學生發展的現實起點已有預設，但畢竟每一節都進行教學前測、課前談話等不太現實，有時在課堂上就可以通過嘗試練習的方式尋找學生的現實起點，尋找到連接新舊知識的橋梁。但由于教學活動是一種雙邊活動，課堂現場千變萬化，再好的教學設計也不能完全把握學生的學習起點，教師要根據兩者之間的差距，采取恰當的教學策略，及時根據課堂教學進程調整教學方式，因學生而動、應情境而變。

總而言之，數學教學活動應客觀地把握學生的邏輯起點，找準學生的現實起點，在邏輯起點的基礎之上，熟悉、鉆研教材的內在聯系。“要把學生引向一個地方，首先得知道他們現在在哪里”，由此可見，從學生的現實起點出發，再加上精心的備課，才能真正做到因材施教。

[參考文獻]

[1] 中華人民共和國教育部.義務教育數學課程標準（2011年版）[S].北京：北京師范大學出版社，2012.

[2]鄭水忠，基于邏輯起點忠于現實起點[J].福建教育，2017.

[3]潘學華，把握學生數學學習的起點[J].小學時代數學在線.2017.

（責編 吳美玲）