測點偏移對水泥混凝土路面板角彎沉測試的影響

劉海軍,王子彬,牛曉霞,李 浩

(1.公路交通安全與應急保障技術及裝備交通運輸行業研發中心，廣東 廣州 510420；2.廣東華路交通科技有限公司，廣東 廣州 510420)

0 引 言

板角脫空是水泥混凝土路面最常見的病害之一，治理板角脫空病害是水泥混凝土路面養護的關鍵，也是延長水泥混凝土路面使用壽命的重要環節，而板角脫空的準確識別是基礎。

JTJ 073.1—2001《公路水泥混凝土路面養護技術規范》[1]規定以板角彎沉值是否超過0.2 mm作為板角脫空的判定標準；JTG D50—2006《公路瀝青路面設計規范》[2]規定用落錘式彎沉儀(FWD)或貝克曼梁彎沉儀進行現場測定；JTG D40—2011《公路水泥混凝土路面設計規范》[3]建議根據板角隅處的多級荷載彎沉測試結果判定板底脫空；JTG E60—2008《公路路基路面現場測試規程》[4]僅給出了瀝青路面彎沉的測試方法和步驟。可見，現階段對于水泥混凝土路面板角彎沉的測量沒有相關規范或操作規程，導致采用貝克曼梁、落錘式彎沉儀(FWD)進行測試時，車輪加載位置、貝克曼梁梁頭及落錘的位置不明確。因此，眾多學者對此類問題開展了大量研究。李想等[5-7]分析了行車荷載作用下車輛參數、路面板參數以及板底脫空對路面結構作用力的影響；王乾[8]分析了在荷載和溫度作用下不同路面板底脫空位置、面積、路面板厚度等因素對水泥混凝土路面板彎沉的影響；曾小軍[9]分析了接縫傳荷、板底脫空狀況、彎沉測試溫度等因素對FWD實測彎沉值的影響，結果表明路面板接縫傳荷、板底脫空狀況對彎沉值影響顯著。可見，現有研究中對板底脫空的檢測及識別方法有較為深入的研究，卻鮮有關于測試位置的不確定性對測試結果可靠性影響的研究。

在此背景下，開展了輪胎加載位置、貝克曼梁梁頭及落錘擺放位置的偏移對水泥混凝土板角彎沉值影響研究，提出采用貝克曼梁彎沉法和FWD測試水泥混凝土板角彎沉時測試位置偏移需控制的范圍，以規范水泥混凝土路面板角彎沉現場測試方法，同時滿足水泥混凝土路面養護的需要。

1 現場測試方案

1.1 準備工作

為避免周邊交通對測試造成影響，選取某舊收費廣場圍閉成的臨時空地。先采用Dynatest-8002型落錘式彎沉儀(FWD)對試驗場的水泥板塊逐板檢測、進行初步的脫空判定，判定原則參照美國《新建和修復路面力學-經驗設計指南》[10]：利用FWD進行5 t-7 t-9 t多級加載后進行線性回歸，當截距≥50 μm時表明板下可存在脫空。根據初步判定的結果選定連續的3塊板作為測試對象，沿行車方向分別命名為A#、B#、C#板。A#、B#、C#水泥板長×寬×厚=600 cm×550 cm×30 cm，水泥板間均設有傳力桿。對A#、C#板水泥板分別采用FWD、貝克曼梁進行彎沉測試。

考慮溫度對彎沉測試結果造成的影響[11-12]，為盡量減小其影響，現場測試選擇天氣晴朗、氣溫變化較小的時間段內完成。

測試前分別對A#、B#、C#水泥板沿縱、橫邊按間隔5 cm布點劃線。沿行車方向約定每塊板右下角、右上角、左下角、左上角分別為點位1、點位3、點位7、點位9，點位采用“板塊編號+點位編號”命名，如C#水泥板右下角為C1，B#水泥板右上角為B3；沿行車方向約定每塊板右縱縫、左縱縫、下橫縫、上橫縫分別為YZ、ZZ、XH、SH，編號采用“板塊編號+縫編號”命名，如C#水泥板右縱縫、下橫縫分別為CYZ、CXH。

移動對象與參照對象之間距離的命名規則約定如表1和表2。如彎沉車右后側輪胎外邊緣接地點(移動對象)與C#水泥板右邊縱縫CYZ(參照對象)的距離為S1。各符號意義如圖1和圖2。

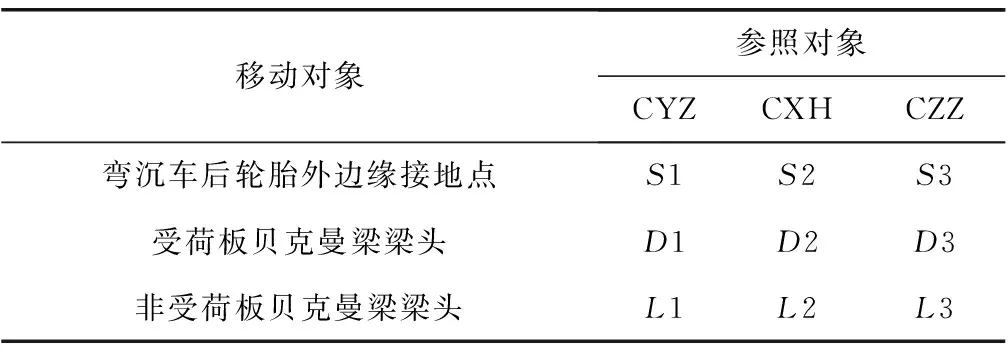
表1 貝克曼梁測試命名規則Table 1 Naming rules in Beckman beam tests

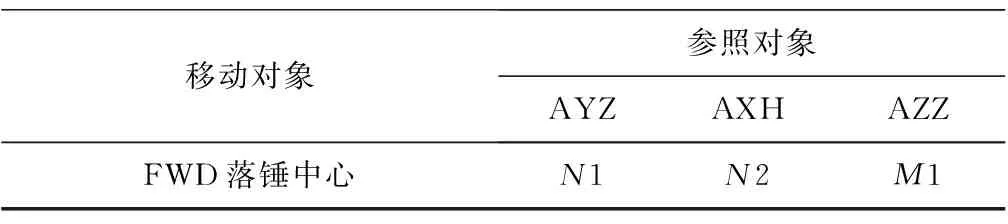
表2 FWD測試命名規則Table 2 Naming rules in FWD tests

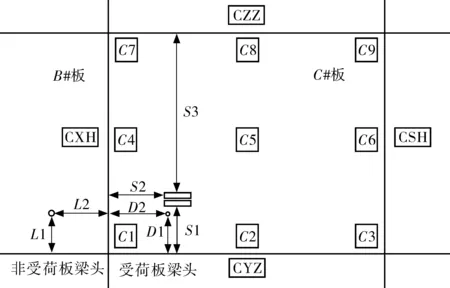
圖1 符號示意(貝克曼梁測試)Fig. 1 Symbols schematic(Beckman beam tests)

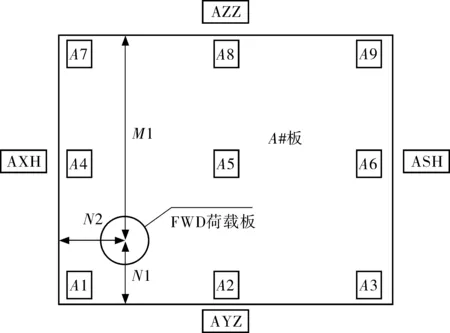
圖2 符號示意(FWD測試)Fig. 2 Symbols schematic(FWD tests)

1.2 測試方案

1.2.1 貝克曼梁測試方案

測試的主要目的在于研究輪胎加載位置和貝克曼梁梁頭擺放位置的偏移對水泥混凝土板角彎沉值影響。每次測試時，同時測試B#非受荷板、C#受荷板的板角彎沉值。

測試總體原則：約定初始位置為輪胎外邊緣、貝克曼梁梁頭與縱縫和橫縫相距5 cm；測點不動時，梁頭始終位于初始位置，僅荷載移動；測點、荷載同步偏移時，梁頭緊貼輪胎外邊緣而同步偏移，且認為梁頭、輪胎外邊緣與縱縫距離相等。

經前期初步篩選，C1板角脫空，C7板角不脫空。針對C1板角有如下3個測試方案：

方案1：測點不動，荷載橫向偏移。保持D1=D2=L1=L2=S2=5 cm，控制S1以研究荷載橫向偏移對彎沉值的影響。控制S1的原則為：S1初始值為5 cm；當S1小于1 m時，依次增加5 cm；當S1大于1 m時，依次增加10 cm，直至S1=210 cm，共測試31次。

方案2：測點不動，荷載縱向偏移。保持D1=L1=L2=5 cm，S1=10 cm，控制S2、D2以研究荷載縱向偏移對彎沉值的影響。控制S2的原則為：S2、D2初始值均為5 cm，依次增加5 cm，直至S2=70 cm，共測試14次。

方案3：測點、荷載同步橫向偏移。保持S2=5 cm，控制S1、L1、L2、D1、D2以研究測試位置偏移對彎沉值的影響。控制S1、L1、L2、D1、D2的原則為：S1、L1、L2、D1、D2初始值均為5 cm，當S1小于1 m時，依次同步增加5 cm；當S1大于1 m時，依次同步增加10 cm，直至210 cm，共測試31次。

針對C7板角有如下兩個測試方案：

方案4：測點不動，荷載橫向偏移。

保持D2=D3=L2=L3=S2=5 cm，控制S3以研究荷載橫向偏移對彎沉值的影響。控制S3的原則為：S3初始值為10 cm，依次增加10 cm，直至S3=100 cm，共測試10次。

方案5：測點、荷載同步橫向偏移。保持S2=5 cm，控制S3、L2、L3、D2、D3以研究測試位置偏移對彎沉值的影響。控制S3、L2、L3、D2、D3的原則為：S3、L2、L3、D2、D3初始值均為10 cm，依次同步增加10 cm，直至100 cm，共測試10次。

1.2.2 FWD測試方案

測試的主要目的在于研究FWD加載位置的偏移對水泥混凝土板角彎沉值影響。

經前期初步篩選，A1、A7板角均脫空。下述方案6針對A7板角，方案7針對A1板角。FWD采用5噸加載模式。

方案6：荷載橫向偏移。保持N2=20 cm，控制M1以研究橫向加載位置對彎沉值的影響。控制M1的原則為：M1初始值為20 cm，依次增加30 cm，直至M1=350 cm，共測試12次。

方案7：荷載縱向偏移。保持N1=20 cm，控制N2以研究縱向加載位置對彎沉值的影響。控制N2的原則為：N2初始值為20 cm，依次增加30 cm，直至N2=350 cm，共測試12次。

2 測試結果分析

2.1 貝克曼梁法測試結果分析

2.1.1 脫空板角C1彎沉測試結果分析

方案1(測點不動，荷載橫向偏移)的測試結果如圖3。

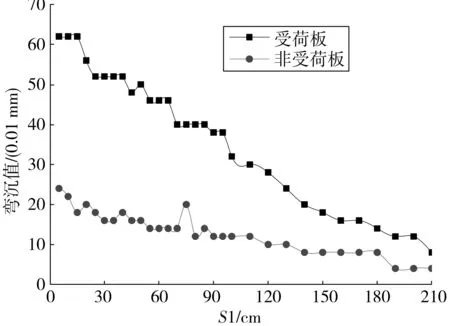
圖3 方案1測試結果Fig. 3 Test results of scheme 1

非受荷板、受荷板板角彎沉值均隨著S1增大呈線性下降趨勢，擬合公式為：

y=-0.262 8×S1+61.2，R2=0.98(受荷板)

(1)

y=-0.079 6×S1+20.3，R2=0.9(非受荷板)

(2)

式中：自變量S1物理意義如圖1；因變量y為受荷板或非受荷板板角彎沉值。

可見，受荷板彎沉下降幅度大于非受荷板。受荷板板角彎沉值對荷載橫向偏移敏感度大于非受荷板，現場測試時，應控制受荷板荷載的橫向位置。

方案2(測點不動，荷載縱向偏移)的測試結果見圖4。

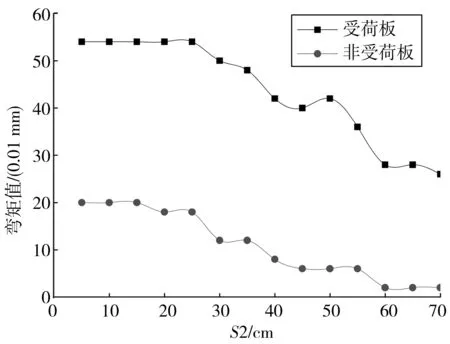
圖4 方案2測試結果Fig. 4 Test results of scheme 2

如圖4，非受荷板、受荷板板角彎沉值均隨著S2增大呈線性下降趨勢，擬合公式為：

y=-0.486 2×S2+61.8，R2=0.91(受荷板)

(3)

y=-0.334 1×S2+23.4，R2=0.95(非受荷板)

(4)

式中：自變量S2物理意義如圖1；因變量y為受荷板或非受荷板板角彎沉值。

與方案1(測點不動，荷載橫向偏移)相比，在自變量S1、S2由5 cm變化至50 cm的范圍內，方案1受荷板彎沉由0.62 mm減小為0.50 mm，方案2受荷板彎沉由0.54 mm減小為0.42 mm，兩者減小幅度相當。表明在一定范圍內，受荷板橫向、縱向偏移對彎沉的影響相當。

方案3(測點、荷載同步橫向偏移)的測試結果如圖5。非受荷板、受荷板板角彎沉值均隨著S1增大呈線性下降趨勢，擬合公式為：

y=-0.211 7×S1+55.8，R2=0.92(受荷板)

(5)

y=-0.049 7×S1+23.9，R2=0.73(非受荷板)

(6)

式中：自變量S1物理意義如圖1；因變量y為受荷板或非受荷板板角彎沉值。

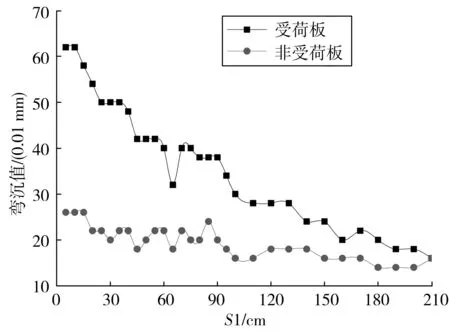
圖5 方案3測試結果Fig. 5 Test results of scheme 3

對比方案3與方案1(測點不動，荷載橫向偏移)的測試結果如圖6。

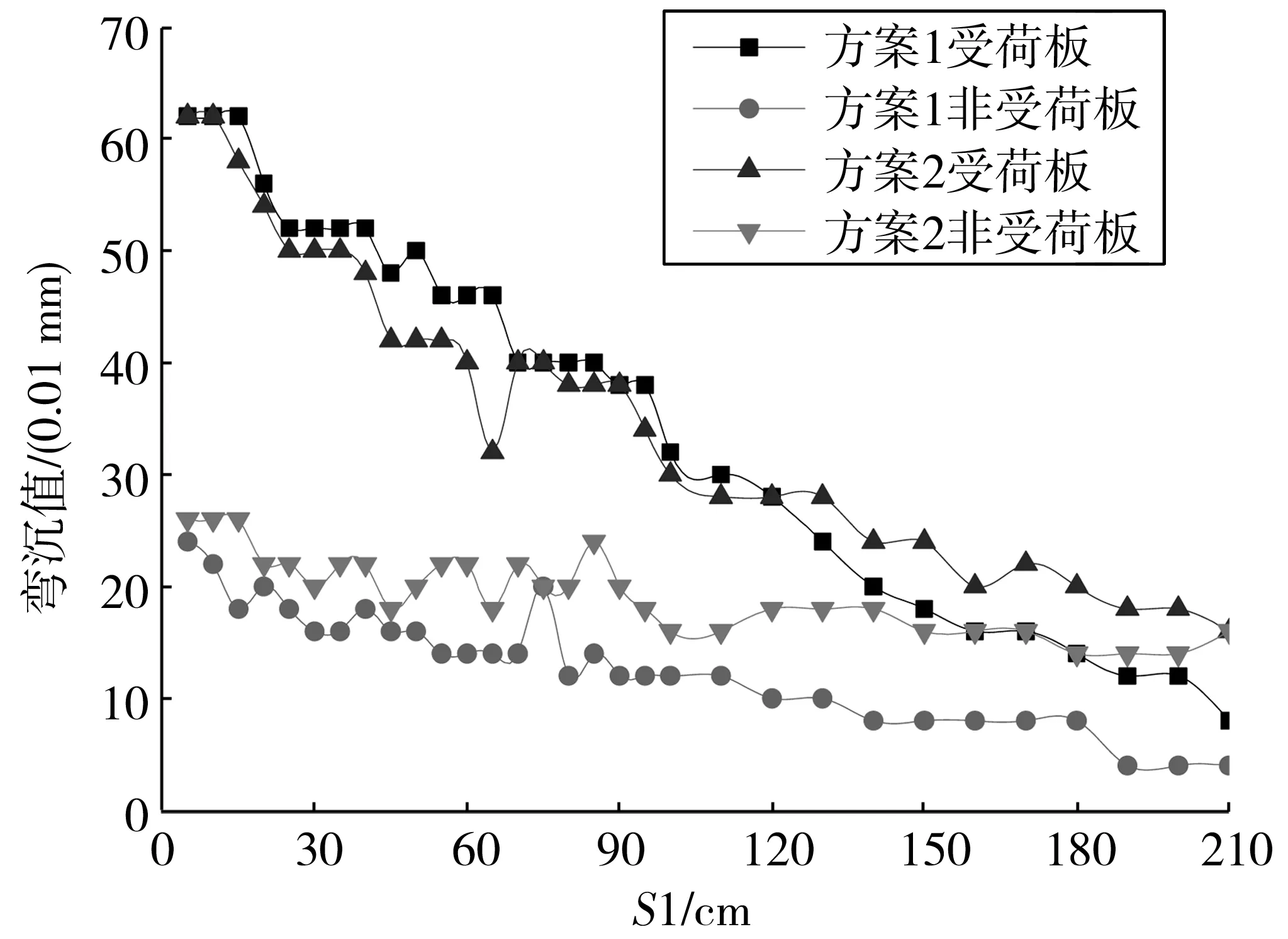
圖6 方案1與方案3對比Fig. 6 Comparisonof scheme 1 and scheme 3

如圖6，對于受荷板，在S1≤120 cm時，方案1測試得到的彎沉值大于方案3；當S1≥120 cm時，方案1測試得到的彎沉值小于方案3。對于非受荷板，方案3測試得到的彎沉值大于方案1。表明受荷板和非受荷板貝克曼梁梁頭的位置對彎沉值的測試結果均有一定的影響。

綜合以上分析可得，各方案的測試結果均表明板角彎沉值與偏移距離呈線性關系。表3給出了各方案在線性擬合下各測點的擬合值，以偏移5 cm的測試值為基準，分別將不同偏移距離下的擬合值與基準值作比較，比值見表3。

如表3，方案1(測點不動，荷載橫向偏移)和方案2(測點不動，荷載縱向偏移)在貝克曼梁梁頭測點不動、僅荷載橫向或縱向偏移的情況下，工程應用容許誤差以5%～10%計算，兩種方案均表明荷載偏移10 cm、20 cm可分別滿足容許誤差5%、10%的要求。

方案3在貝克曼梁梁頭測點和荷載同步橫向偏移的情況下，工程應用容許誤差以5%～10%計算，結果表明同步偏移10 cm、20 cm可分別滿足容許誤差5%、10%的要求。

考慮貝克曼梁測試時輪胎、梁頭位置的擺放習慣(沿行車方向，梁頭總是位于輪胎的外側)，相對于初始位置，梁頭只要在在輪胎荷載橫向或縱向偏移10～20 cm的范圍內，可以滿足容許誤差5%～10%的要求，但建議梁頭盡量位于初始位置。

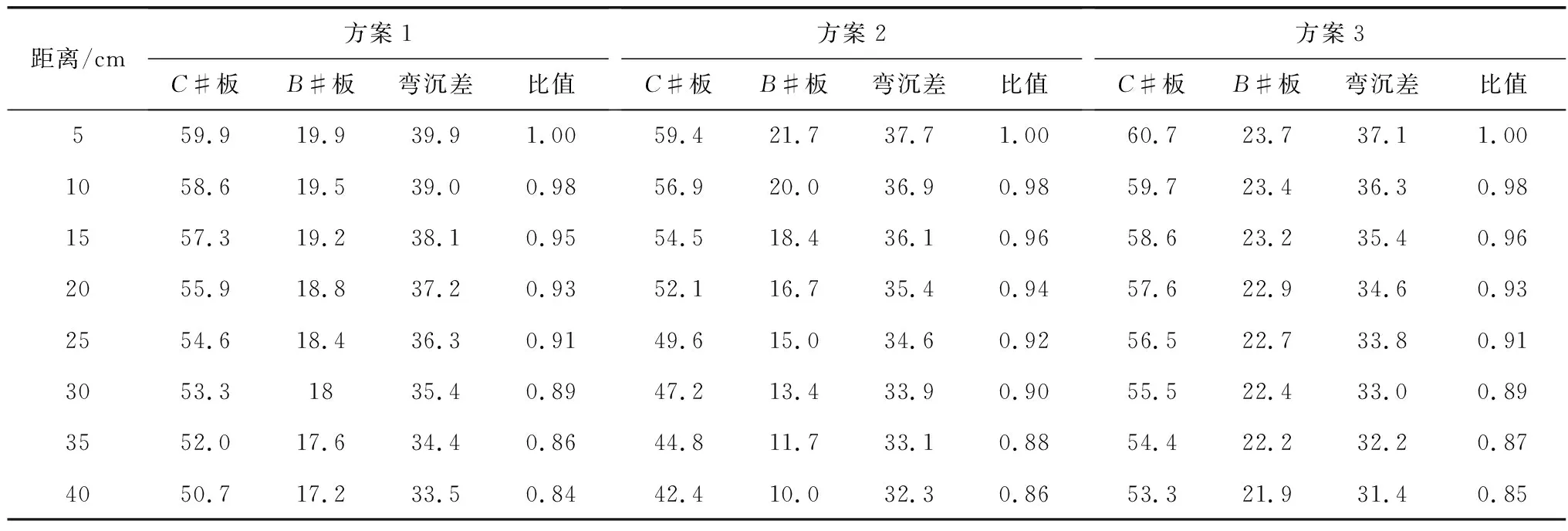
表3 貝克曼梁3種方案擬合結果Table 3 Fitting results obtained by three kinds of schemes of Beckman beam

2.1.2 非脫空板角C7彎沉測試結果分析

方案4和方案5的彎沉測試結果如表4。

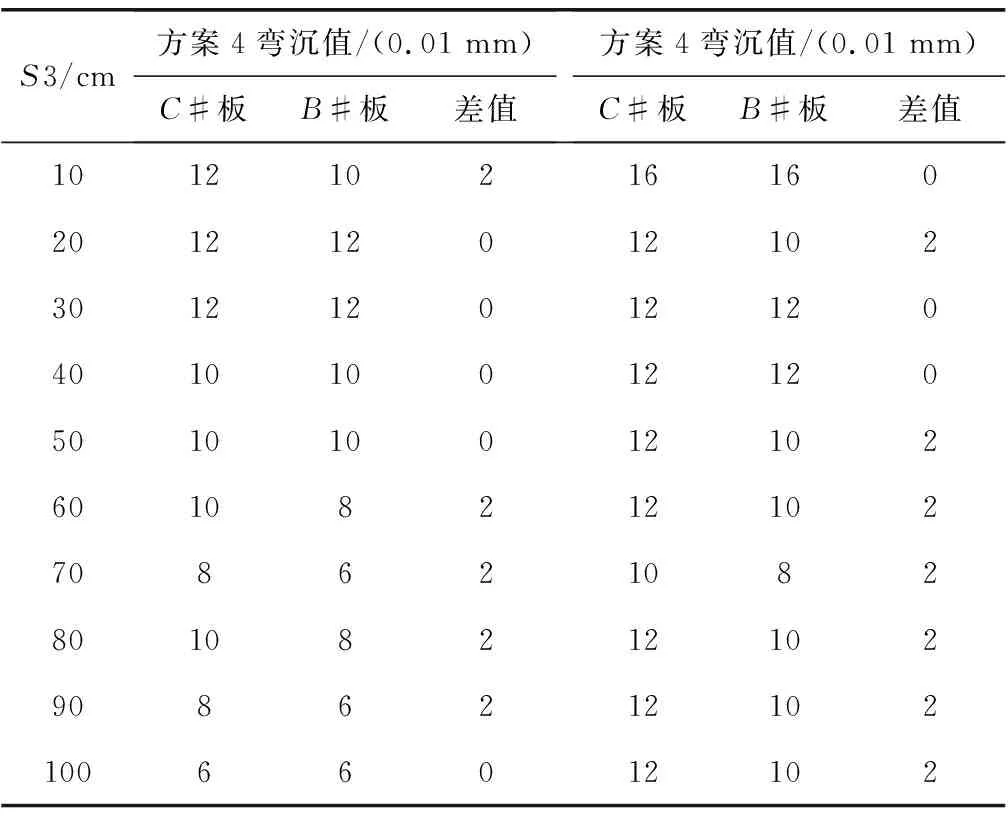
表4 非脫空板角C7彎沉測試結果Table 4 Deflection results of C7

如表4，方案4測試結果表明在板角不脫空時，荷載的偏移對測試結果無影響；方案五的測試結果表明，在板角不脫空時，測點的偏移對測試結果也無影響。

2.2 FWD測試結果分析

FWD方案6、方案7測試結果如表5。

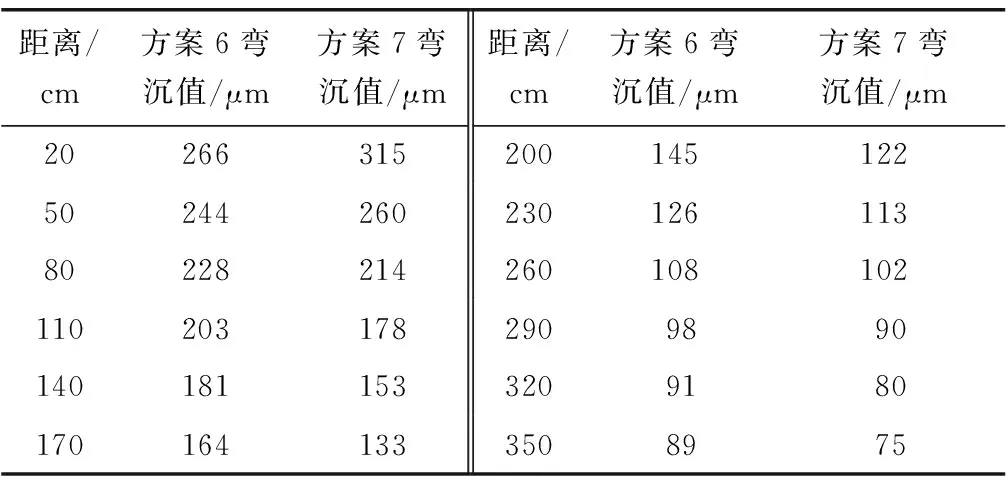
表5 FWD彎沉測試結果Table 5 Deflection results of FWD

如表6，A1、A7板角彎沉值隨著N2、M1增大呈線性下降趨勢，擬合公式為：

y=-0.6565×N2+274，R2=0.88(A1板角)

(7)

y=-0.5715×M1+268，R2=0.98(A7板角)

(8)

式中：自變量N2和M1物理意義如圖2；因變量y為受荷板或非受荷板板角彎沉值。

由以上分析可得，方案6和方案7的測試結果均表明板角彎沉值與偏移距離呈線性關系。表6給出了兩個方案在線性擬合下各測點的擬合值，以偏移20 cm的測試值為基準，分別將不同偏移距離下的擬合值與基準值作比較，比值見表6。

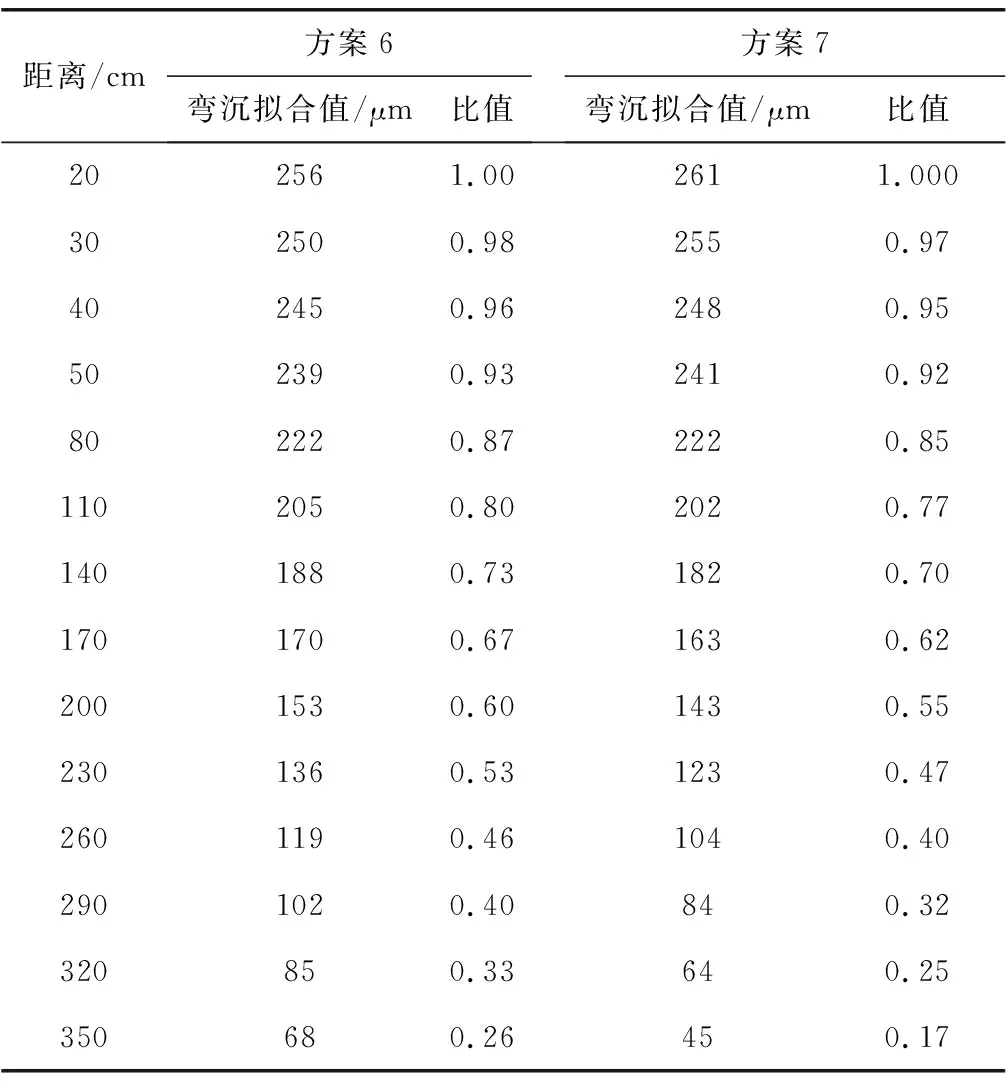
表6 FWD兩種方案擬合結果Table 6 Fitting results obtained by two kinds of schemes of FWD

考慮偏移距離對彎沉測試結果可靠性的影響，工程應用容許誤差以5%～10%計算，3種方案一致表明偏移20 cm可滿足容許誤差5%的要求，偏移30 cm可滿足容許誤差10%的要求。

3 結 語

通過利用貝克曼梁彎沉儀、落錘式彎沉儀開展了輪胎加載、貝克曼梁梁頭及落錘位置的偏移對水泥混凝土板角彎沉值影響研究，得到如下結論：

1)在板角脫空的情況下，兩種方法測試得到的彎沉值均與偏移距離存在較好線性相關性，隨著偏移距離的增加，板角彎沉近似線性減小。

2)貝克曼梁法檢測板角彎沉時，荷載偏移10 cm、20 cm以內可分別滿足工程應用容許誤差5%、10%的使用要求，貝克曼梁梁頭建議擺放于距板角橫、縱縫5 cm的位置。

3)落錘式彎沉儀檢測板角彎沉時，偏移20 cm、30 cm以內可分別滿足工程應用容許誤差5%、10%的使用要求。