根軌跡法在數字控制系統的應用研究
韓 巍
?
根軌跡法在數字控制系統的應用研究
韓 巍
(武漢船用電力推進裝置研究所,武漢 430064)
本文以直流伺服電機為例,介紹了根軌跡在有傳遞函數和狀態空間兩種狀況下在數字控制系統的具體應用。應用于傳遞函數時,由于校正器零極點對輸出性能影響很大,因此需要不斷對系統的根軌跡進行改進,這種方法依賴經驗,但是計算簡單,易于工程實踐。應用于狀態空間時,根據控制系統的性能指標確定閉環系統的主導極點,調節器參數與閉環系統的性能指標建立了量化關系,設計過程概念清晰,簡潔明了,但是計算量比較大。
根軌跡 數字控制 傳遞函數 狀態空間
0 引言
根軌跡法自從1948年被W.R.Evans提出以后,由于其用作圖的方法表示特征方程的根與系統性能之間的關系,不直接求解特征方程,簡單易行,在控制系統的分析與設計中得到廣泛的應用。根軌跡法具有直觀的特點,利用系統的根軌跡可以分析結構和參數已知的閉環系統的穩定性和瞬態響應特性,還可分析參數變化對系統性能的影響。在設計線性控制系統時,可以根據對系統性能指標的要求確定可調整參數以及系統開環零極點的位置,因此根軌跡法可以用于系統的分析與綜合。另一方面,由于數字控制相對于模擬控制有許多優越之處,特別是近幾年隨著處理器等微電子技術突飛猛進的發展,數字控制的硬件平臺日益更新更加快數字控制的推廣應用,使之受到廣泛關注。由于數字控制存在采樣、保持等環節,其控制設計和模擬控制有很大不同,因而,研究根軌跡法在數字控制系統的應用很有必要。本文將以直流伺服電機為例,分別介紹根軌跡在傳遞函數和狀態方程這兩種描述方法下的具體應用,并比較其優缺點。
1 直流伺服電機控制
1.1 直流伺服電機控制模型
直流伺服電機電樞電壓由反電動勢和內阻壓降兩部分組成。其中,內阻壓降等于電樞電阻乘以電樞電流,由于電樞電阻為常數,內阻電壓與電樞電流成正比;電機轉速和反電動勢成正比,直流伺服電機轉速控制可以等效為反電動勢電壓的控制。反電動勢無法直接控制,需要由電樞電壓間接控制,此時電樞電流可以理解為擾動信號。
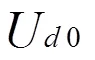
本文研究對象直流伺服電機=0.2W,C=10/41,T=14/41,則圖1可以轉化為圖2的形式。

圖1 額定勵磁下直流伺服電機的動態結構圖
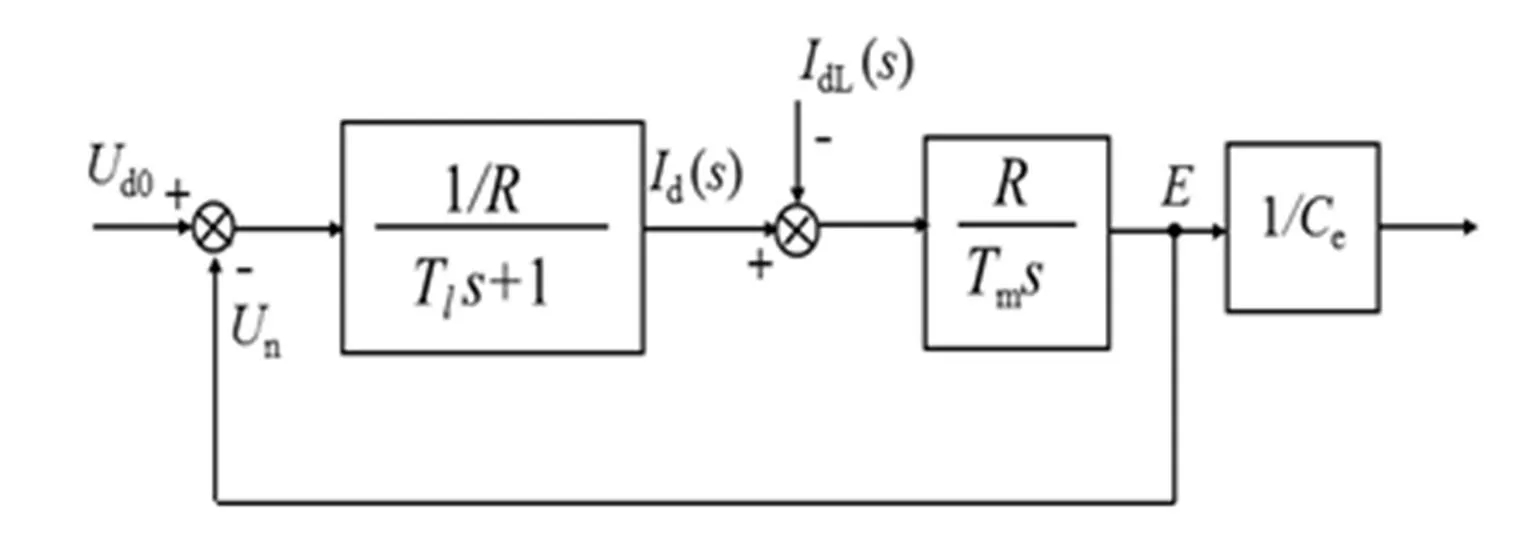
圖2 額定勵磁下直流電動機的函數圖
1.2 傳遞函數下的控制模型

圖3 Ial = 0時動態結構圖的簡化形式與傳遞函數
1.3 狀態空間下的控制模型

式中,
在數字控制下,常常采用零階保持器(ZOH)。采用周期采樣的離散方式,采樣周期設為T時,經過零階保持器后,逆變器連續時間狀態方程式(1)離散化后,可得:
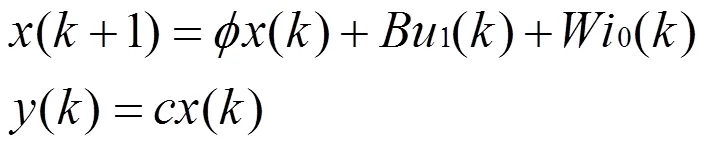
2 根軌跡法在傳遞函數的應用
數字控制器有兩種設計方法:模擬化方法和直接數字法。在采樣周期足夠小的情況下,把基于連續系統設計的模擬控制器離散化來得到數字控制器,為模擬化方法。但是,這種數字控制器設計方法只是一種近似處理,不能實現只有數字控制特有的控制策略。直接數字法就是對加采樣保持器的被控對象離散化模型進行數字控制器設計。直接數字法在保持系統穩定的同時可得到更寬的控制帶寬,這個優點在多環系統或采樣周期較大時變得更為顯著,所以數字控制器最好采取直接數字化方法設計,本文就采取這種方法。
2.1 被控模型的離散
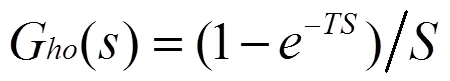
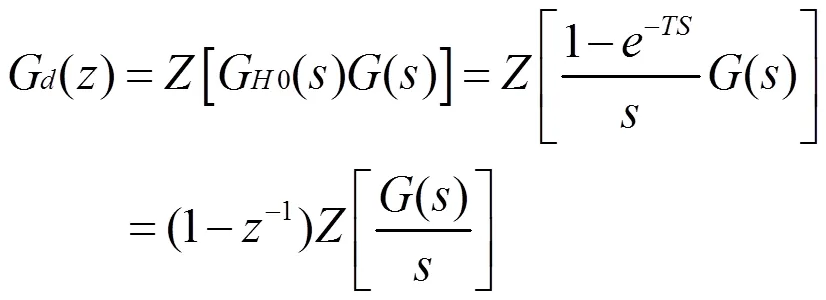
針對本研究對象直流伺服電機,可得:
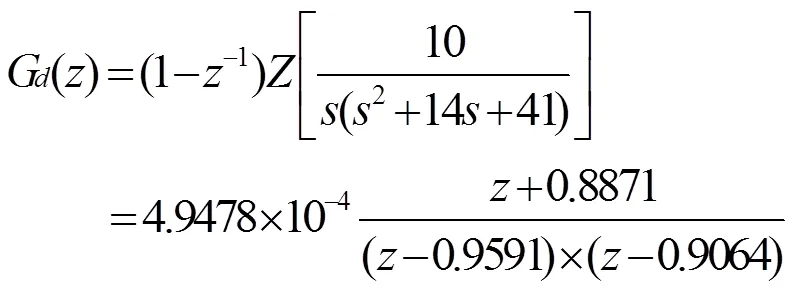
2.2 離散根軌跡設計
離散根軌跡的設計分為以下幾個步驟:
a根據性能要求,確定閉環極點的允許范圍;
b獲得控制對象離散模型;
c根據純比例控制的根軌跡,選擇校正器;
d設計(),并反復循環修改。
本文研究對象超調、穩定時間的要求為,T£0.015 s,£2,=0.01s ;運用matlab畫出僅為比例控制的根軌跡如圖4所示。
可以看出,純比例控制時,系統很容易不穩定,況且無論K取何值,閉環極點都不可能進入期望的區域,本文以超前校正為例討論根軌跡在傳遞函數校正的應用,當考慮適當抵消=0.9591時的極點,則超前校正器可以形如(-0.9594)/(-))的形式[2]。圖5是pole逐步向(-1,0)靠近,分別取值{0.6146,0.1146,-0.1146,-0.4146,-0.8146}時的根軌跡圖。

圖4 純比例調節時的根軌跡圖

圖5 pole變化時的根軌跡圖
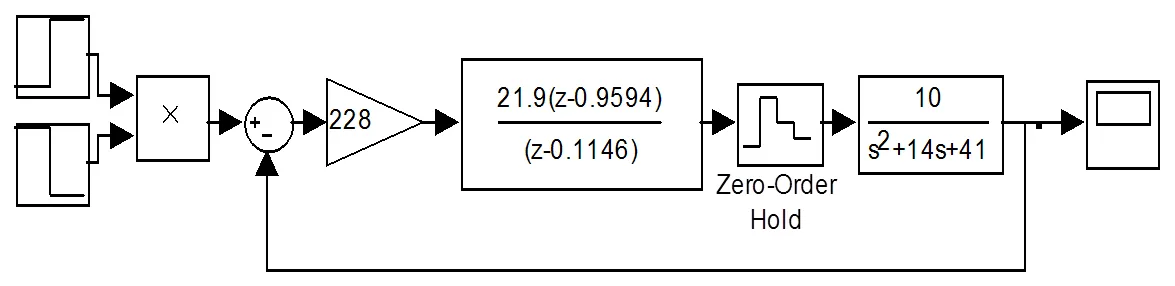
圖6 控制系統方框圖
根據性能指標要求,選取適當的,在不同極點處的響應如圖6所示。從圖6可以看出,值不同時,有不同的響應,在=0.1146時性能最好,此時T= 0.016 s,=1.9,滿足指標要求。由于s域內的超調、調節時間都可以轉化為z域的極點要求,因而可以看出,并不是越小越好,而是有一定的限制范圍,超出范圍,會引起超調增加,響應變慢等問題。
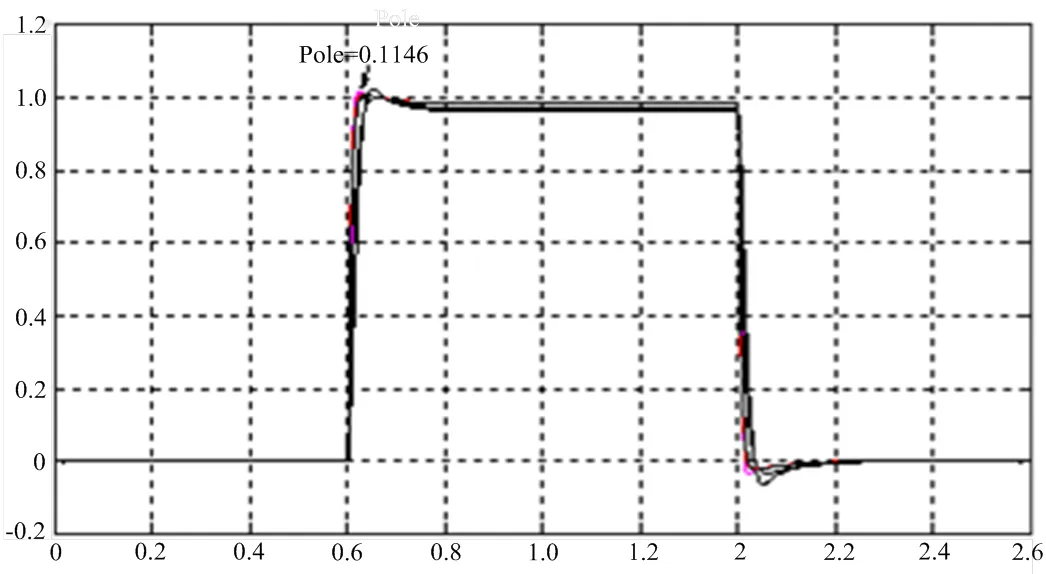
圖7 pole變化時的響應
以上研究了根軌跡法在傳遞函數的應用,通過直流伺服電機轉速控制的例子可以發現,應用于傳遞函數時,根軌跡法簡單、有效,且易于實現,但是需要憑借經驗進行多次的“試湊”。
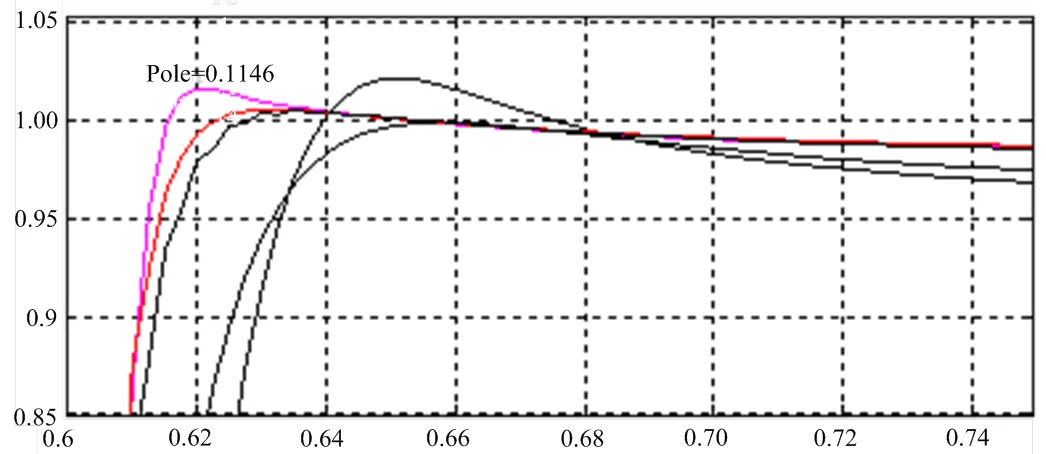
圖8 極點變化時響應的局部放大圖
3 根軌跡法在狀態空間中的應用
由于PI、PD、PID控制自由度小于閉環極點數,不能對其進行任意配制,也就是不能很好地改善系統的動、靜態性能;而且在實際情況中不可避免的存在擾動作用,致使系統穩態時不能理想地跟蹤參考輸入而產生誤差,因而在實際情況中,對狀態方程下可以采取偏差積分的方式[3]。也稱為狀態增廣系統數字控制。
在此基礎上,則可以引入偏差量的積分
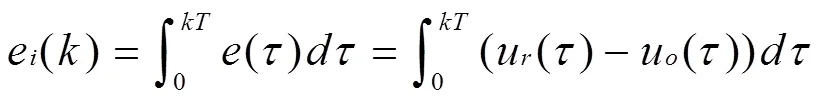
由此,可獲得直流伺服電機狀態空間方程為:
輸出狀態方程為:
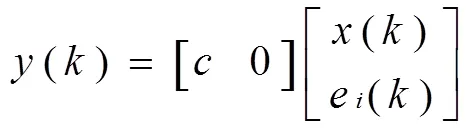
在滿足(8)的條件時,此系統完全能控,因而就可以用狀態反饋實現閉環極點的任意配制,就可以保障系統的穩定性、動態性能以及減小穩態誤差。
1π/(k=1,2……) (8)
由于可以用狀態反饋實現閉環極點的任意配制,首先,假設反饋增益矩陣為,則直流伺服電機偏差積分狀態反饋控制系統方框為圖9。
將反饋增益矩陣帶入(6)式,可得:

閉環系統特征方程為:

如果希望的閉環極點確定的特征方程為:

結合(10)和(11),可以求得反饋增益矩陣。在同樣的要求下,可以設置如下參數:=0.8,=5000,=10,采樣周期=50ms,計算求得1=3.0660*10^6,2=0.0003*10^6,k=0.4324*10^6。圖9和圖10顯示了直流伺服電機對指令跟蹤,給定為單位階躍信號,在=0.08 s、=0.12 s時候突加、突減負載。從圖10可以看出,T=0.01 s,=2.1,仿真波形表示此控制效果很好,滿足性能要求。更重要的是,此種設計方法對負載電流也有很好的抑制效果。
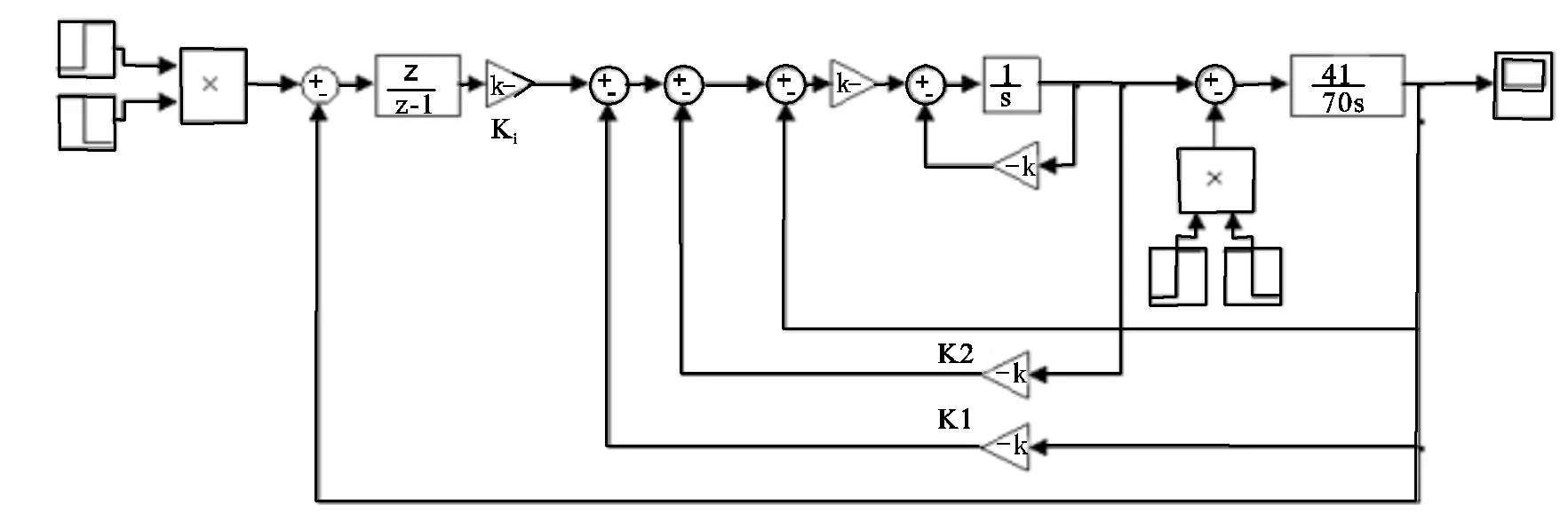
圖9 直流伺服電機積分狀態反饋控制系統方框圖
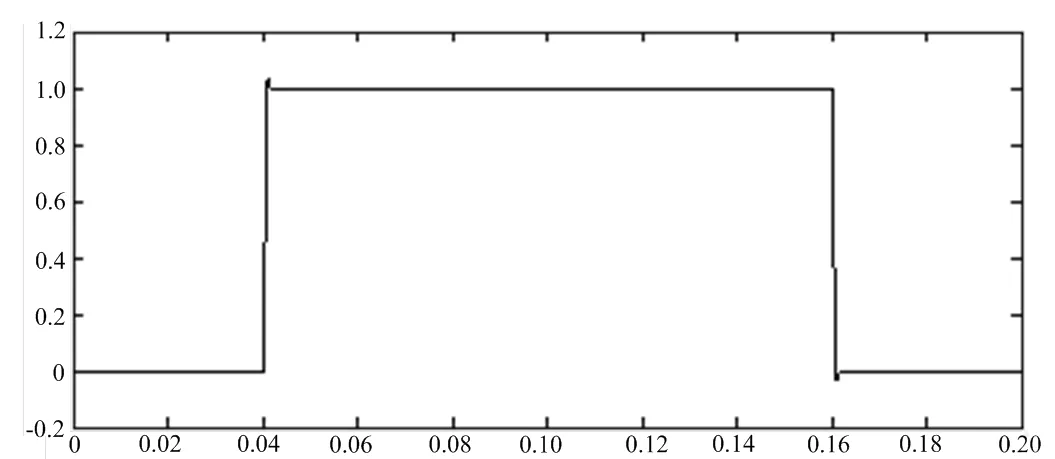
圖10 直流伺服電機動態指令跟蹤
以上研究了根軌跡在狀態方程中的應用,可以發現,在保持系統完全能控的前提下,可以通過反饋增益矩陣的合理選擇將極點配置在滿足性能指標的位置上,建立了量化關系,設計過程概念清晰,簡潔明了,控制性能比前面需要依靠經驗的效果好。但是,此種方法計算比較復雜,且在狀態變量不能直接測量的情況下需要構造狀態觀測器,對處理器等電力電子器件的要求比較高。

圖11 直流伺服電機動態指令跟蹤局部放大圖
4 總結
本文介紹了根軌跡在傳遞函數和狀態空間這兩種描述方法下的具體應用。在應用于傳遞函數時,需要不斷對系統的根軌跡進行改進,超前、滯后等校正器的零極點特別是極點對數字控制輸出性能的影響很大,這種方法比較依賴經驗,但是此種方法且易于工程實踐。在應用于狀態空間時,通過增益反饋矩陣可以與性能指標建立量化關系,對負載擾動有很好的抑制作用,設計過程概念清晰,簡潔明了,控制性能也比較好;缺點就是計算比較復雜,且有可能需要構造狀態觀測器,對器件的要求比較高。實際工程中,要綜合各方面因素綜合考慮確定數字控制方案。
[1] 陳伯時. 電力拖動自動控制系統(第二版. 北京: 機械工業出版社, 1992.
[2] 楊國安. 數字控制系統-分析設計及其實現[M]. 陜西: 西安交通大學出版社, 2008.
[3] 彭力. 基于狀態空間理論的PWM你變電源控制技術研究. [D]. 武漢: 華中科技大學圖書館, 2004.
Research on Application of Root Locus Method in Digital Control System
Han Wei
(Wuhan Institute of Marine Electric Propulsion, Wuhan 430064, China)
.
TP13
A
1003-4862(2018)12-0040-04
2018-09-12
韓巍(1977-),男,本科。研究方向:電機控制。E-mail: 13667228872@163.com

