斜激波總壓損失率極小值理論解與物理意義

史愛明，Earl H DOWELL

1. 西北工業大學 航空學院 NPU-Duke空氣動力與氣動彈性聯合實驗室，西安 710072 2. 杜克大學 普拉特工學院 NPU-Duke空氣動力與氣動彈性聯合實驗室，達勒姆 27708-0300

斜激波關系式與其圖解是人們獲得激波角和激波前后流動參數的重要方法[1-3]。根據經典激波理論[1-2]，斜激波關系式為定常、絕熱的平面斜激波無黏流動問題解析解。為便于激波角的求解，1953年，美國國家航空咨詢委員會(National Advisory Committee for Aeronautics, NACA)Ames中心的研究人員制作出斜激波關系式圖解，即通常空氣動力學研究者所熟悉的θ-β-Madiagram(θ為楔形角，β為激波角，Ma為馬赫數)[3]。

本文的研究起因來自Anderson所著《Fundamentals of Aerodynamics》中第9章第2節給出的θ-β-Ma圖第4條規律：固定物面楔形角為20°，考查激波強度隨來流馬赫數的變化情況；書中給出了馬赫數5.0的激波強度大于馬赫數2.0的激波強度舉例。此結論是正確的，但如果繼續降低激波前的馬赫數，激波強度是會持續下降嗎？之后的研究表明，激波強度不是持續下降的，激波強度最小值出現在激波角為55°時所對應的波前馬赫數1.959。 進一步研究，得到了實現總壓損失率極小值控制的解析方程組，當然也是激波強度最弱條件的理論解：激波角關于楔形角的直線方程，且控制方程與馬赫數和斜激波關系式都是無關的。

氣體的可壓縮性和聲波傳播速度的有限性，使激波成為自然界與人工設計超聲速流中必然產生的物理現象。激波是一種氣流參數梯度變化很大且極薄的流動結構，通常認為激波的厚度約為100 nm。激波結構雖然薄，但耗散性很大。它是導致飛機超聲速飛行激波阻力的直接原因[4]。歐洲空客公司、德國宇航院和法國航空航天中心等科研機構的共同研究表明：對一精細設計的高速翼身組合體模型，馬赫數2.0的升阻比比馬赫數0.95的升阻比降低了37.21%[5]。激波強度增加是導致升阻比降低的主要原因。此外，阻礙超聲速飛行的另一個重要問題是音爆問題[6-8]。激波強度仍然是決定音爆強弱的主要物理因素。定義適用的激波強度物理量，尋找激波強度控制規律，對生成高效率的超聲速流是有幫助的。

激波理論計算[9-12]、實驗設計[13-16]與理性分析[17-19]是空氣動力學重點關注的問題。20世紀80年代，張涵信結合熵增條件建立的無波動、無自由參數耗散格式對提高激波計算分辨能力起了實質性作用[20-21]。之后，鄧小剛等發展的高階精度耗散加權緊致非線性格式在解決強激波渦量場非物理振蕩問題中發揮了巨大作用[22-23]。計算格式檢驗會依賴于激波強度這一重要物理量。發動機超聲速進氣道的總壓恢復系數也有賴于管流激波強度規律研究[24-27]。高效乘波體氣動布局設計[28]和超聲速等離子流動控制總壓損失量也與激波強度規律有理論關聯[29]。天文中的星際激波現象理解[30]、弱激波數學存在性原理研究[31]等問題或也可從斜激波強度規律中得到啟發。此外，斜激波強度規律理論解亦有望為高精度保真計算格式驗證設計檢驗標模[32]。更為重要的是，氣流總壓值是表征流體輸出有用機械功能力的指標性參數，所以斜激波總壓損失率極小值解析方法與效率圖解或將能實現超聲速流中空氣動力最大有用功能力的物理極限。

本文第1節，基于法向馬赫數定義和斜激波關系式，導出以法向馬赫數表示的特殊斜激波關系式，分析得到斜激波總壓損失率極小值控制方程。第2節，結合總壓損失率極小值控制方程，以斜激波總壓損失率變化規律為研究指引，生成斜激波氣動效率圖解。第3節，以10°楔形角為例解釋斜激波等值總壓損失率的雙解特性。第4節，對比斜激波氣動效率圖解法與總壓比直接圖解法的研究差異。第5節，以《Fundamentals of Aerodynamics》書中斜激波關系式規律4為源，演繹應用理論方程和效率圖解控制平面超聲速流中的激波強度。

1 方程導出

采用法向馬赫數作為斜激波強度表征量。法向馬赫數定義為

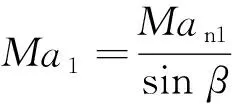
(1)

式中：Ma1為激波波前馬赫數；β為激波偏轉角。

將式(1)中導出式代入斜激波關系式[1]，經適當三角公式代換運算(具體推導見附錄A)，可得到關于激波角和楔形角的法向馬赫數斜激波關系式(2)。斜激波關系式是在定常和絕熱假設下、忽略(除激波內層外)氣體黏性與體積力的斜激波超聲速流動問題的解析解。式(2)是斜激波關系式的法向馬赫數特殊表達式，其適用條件與斜激波關系式是一致的。

(2)

式中：θ為物面楔形角；γ為氣體比熱比。對于理想氣體(無特殊說明，文中流體均為理想氣體)：γ= 1.4時，θ取值范圍為[0°，45.58°)。如固定θ， 由式(2)可看出：當2β-θ=90°時，式(2)左端法向馬赫數將取得最小值。對斜激波而言，它是實現固定θ的最弱激波強度條件。因此，在得出最小法向馬赫數的控制方程同時，也得到了實現平面斜激波最弱激波強度條件的控制方程，即

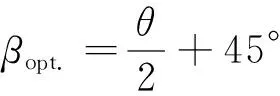
(3)

式中：βopt.為對應總壓損失極小值的最優激波角。聯立式(2)和式(3)，進一步可得到固定物面楔形角情況下，實現法向馬赫數最小值控制的斜激波方程為

(4)

斜激波總壓損失率是法向馬赫數的唯一函數，且是法向馬赫數的單調增函數。總壓損失率公式推導和函數單調性證明見附錄A。直接給出實現總壓損失率極小值控制的方程組為

(5)

式中：Δp=p01-p02為斜激波前后總壓損失量，p01和p02分別為激波前與激波后的總壓。

2 方程圖解法

2.1 總壓損失率極小值圖解

將總壓損失率極小值控制方程式(3)繪制于斜激波θ-β-Ma圖上，即可得到實現總壓損失率極小的氣動效率圖解——θ-β-Ma圖上的一條直線(固定θ的氣動效率極大值)，如圖1所示。

圖1中，總壓損失率極小值直線(紅色粗實線)與強弱解分界線(點劃線)，將斜激波氣動效率圖解分成3個部分。其中，第②部分和第③部分是與斜激波總壓損失率規律直接相關的區域。區域①為斜激波強解區，總壓損失率大于區域②和③，一般不獨立存在。對于固定的楔形角(如θ=20°)：

1) 在區域②中，隨著波前馬赫數增大(沿灰色箭頭向下)，斜激波總壓損失率值逐漸減小，最小總壓損失率直線與θ=20°的垂線交點處(黑色實三角形點)，激波總壓損失率達極小值。對于給定楔形角，區域②是總壓損失率值大且馬赫數小的區域。從氣動效率角度考慮，在設計超聲速流時，不應選擇總壓損失大的區域②中的馬赫數作設計馬赫數。

2) 區域③中，沿箭頭繼續向下，隨著馬赫數增大，總壓損失率值也增大。因此，若以取得最小總壓損失率為目的，可定義最小總壓損失率直線上的波前馬赫數為最優馬赫數Ma1,opt.。

特別的是，圖1中標出的物面楔形角為20°時最優馬赫數Ma1,opt.=1.959，是從《Fundamentals of Aerodynamics》書中馬赫數5.0與2.0激波強度推論分析中發現的。將馬赫數2.0減小0.041就可得到20°楔形角的最優馬赫數。更重要的是，馬赫數再減小，激波的總壓損失率值卻是增加的。

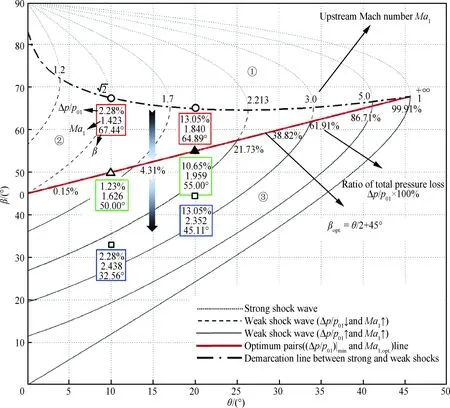
圖1 斜激波氣動效率θ-β-Ma圖Fig.1 θ-β-Ma aerodynamic efficiency diagram for oblique shock

2.2 總壓損失率極小值線上的變參分析

利用總壓損失率極小值線上激波角與楔形角的線性關系式(3)，可將斜激波法向馬赫數特殊形式簡化為只關于楔形角或最優馬赫數的函數。圖2 中給出了總壓損失率極小值隨最優馬赫數、物面楔形角，斜激波最優法向馬赫數隨最優馬赫數、物面楔形角的變化趨勢與計算公式。

圖2 斜激波最小總壓損失率直線上總壓損失率、法向馬赫數變化趨勢Fig.2 Variation trends of ratio of total pressure loss and normal Mach number on the line for minimum ratio of total pressure loss by oblique shock

2.3 斜激波總壓損失率三維分布圖

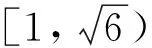
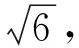
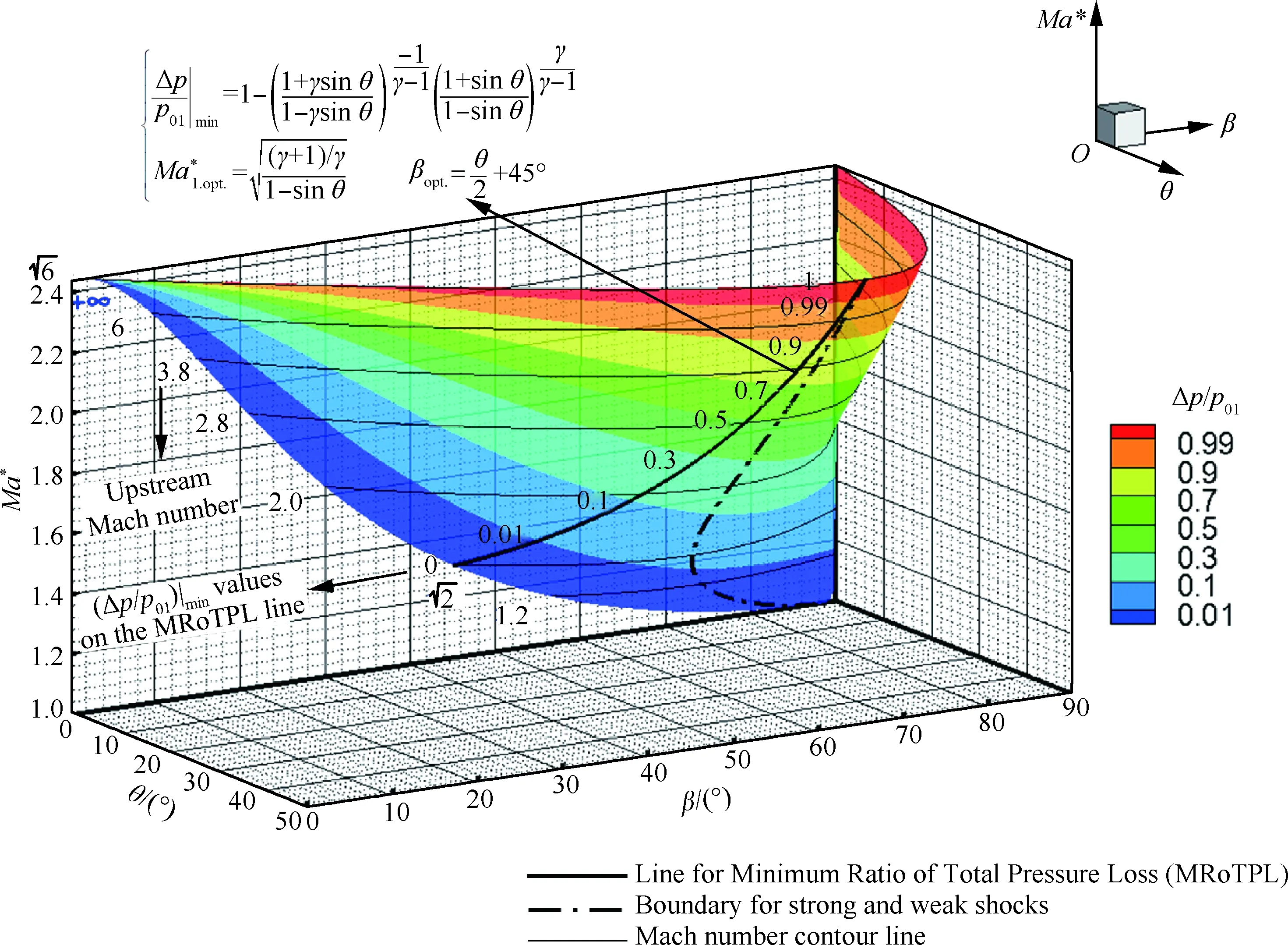
圖3 總壓損失率空間分布規律θ-β-Ma*氣動效率圖Fig.3 Three-dimensional contour figure for ratio of total pressure loss in θ-β-Ma* frame of reference

3 Ma1與β雙解特征

3.1 關于總壓損失率極小值線對稱的雙解現象

總壓損失率極小值線出現在斜激波弱解區域中間。取定物面楔形角，將導致在總壓損失率極小值線兩側出現相同總壓損失率值對應兩組馬赫數和激波角：一組大馬赫數、小激波角；另一組小馬赫數、大激波角。稱此為關于總壓損失率極小值線對稱的等總壓損失率值雙解現象。

圖1中以物面楔形角10°和20°示例雙解現象。例如：10°楔形角，總壓損失率值都為2.28%，紅色框中為小馬赫數Ma1=1.423、大激波角β=67.44° 的解；藍色框中為大馬赫數Ma1=2.438、小激波角β=32.56°的解。

3.2 10°楔形角的Ma1與β雙解形成分析

式(5)表明，法向馬赫數與總壓損失率變化規律是相同的。相對總壓損失率公式，采用法向馬赫數進行雙解特性分析是便利的。

圖4中為法向馬赫數Man1雙解形成的馬赫數與激波角轉化關系。圖4中除一對圓環(小Ma1、大β)與方格(大Ma1、小β)雙解點外，還給出1#與1##、3#與3##兩對雙解值。需指出，圖4(b) 中Man1的激波角雙解關系是關于總壓損失率最小的激波角為50°的完全對稱形式。圖4(a)中Ma1與sinβ合成Man1的過程，小Ma1、大β與大Ma1、小β都可形成相同的Man1。其機制或解釋為：物理壓縮(馬赫數)與空間壓縮(激波角)都可取得相同效果的兩組解。

將斜激波法向馬赫數與同值正激波馬赫數對比(圖5)，易知：斜激波流動參數(總壓損失率Δp/p01、靜溫比T2/T1、靜壓比p2/p1、密度比ρ2/ρ1)都存在馬赫數與激波角雙解特性；正激波無雙解特性，是單值函數。對于10°楔形角，馬赫數雙解區間為[1.421, 2.438]，相應激波角雙解區間為[67.42°, 32.58°]；法向馬赫數區間為[1.245, 1.312]。

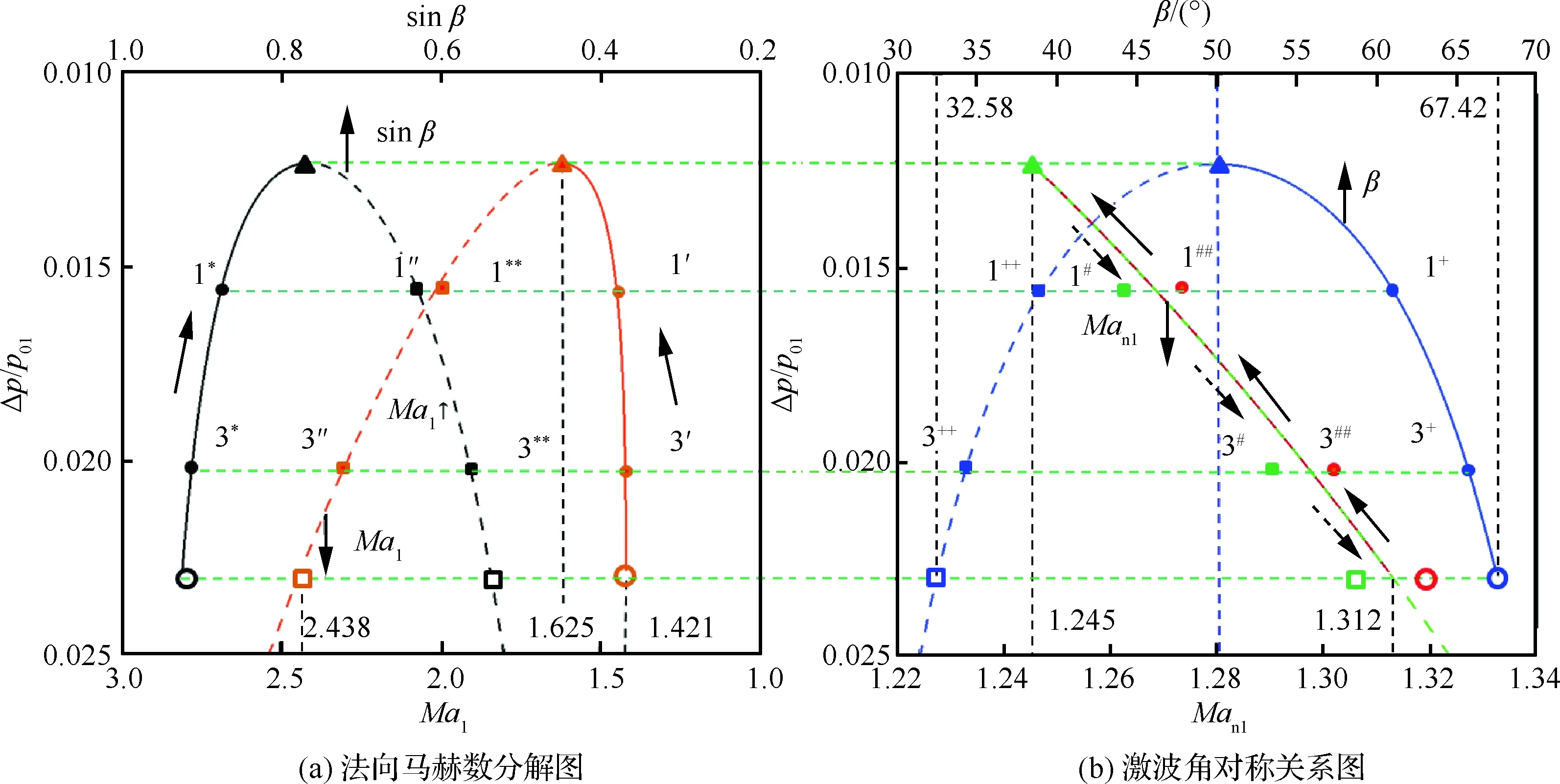
圖4 法向馬赫數相同的馬赫數與激波角雙解形成說明圖(θ=10°)Fig.4 Two-solutions properties for corresponding Mach number and shock angle at same normal Mach number (θ=10°)

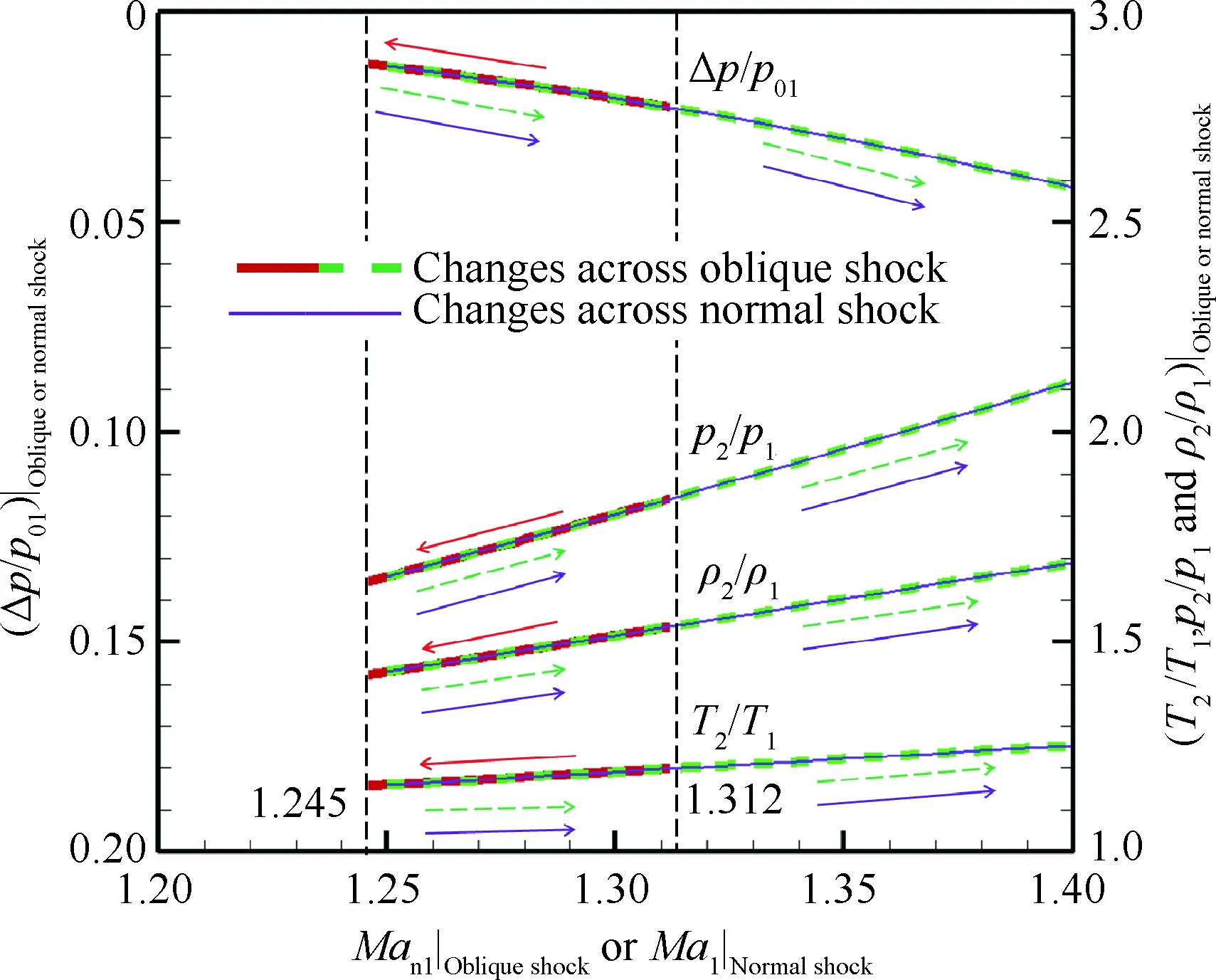
圖5 斜/正激波流動參數變化趨勢Fig.5 Variation trends of flow parameters for oblique/normal shock

4 研究對比

考查激波總壓變化規律時，以總壓比作為馬赫數和楔形角函數是較為自然的研究思路。Shapiro撰寫的麻省理工學院經典著作《The Dynamics and Thermodynamics of Compressible Fluid Flow (Volume 1)》也是采用總壓比參數直接數值法作圖[33]。根據書中圖16.6b的圖解(1953年版的英文原著在第538頁)，對比θ-β-Ma效率圖解法和總壓比直接圖解數據與方法。特別說明的是，圖6中的紅色最大總壓比映射線是未在Shapiro書中予以標出的。圖6中用紅色虛線輔助標注出楔形角20°時，激波前后總壓比，以及相應馬赫數的Shapiro圖解測量值。Shapiro的計算值與圖1中總壓損失率值是吻合的，最優馬赫數值也是一致的。

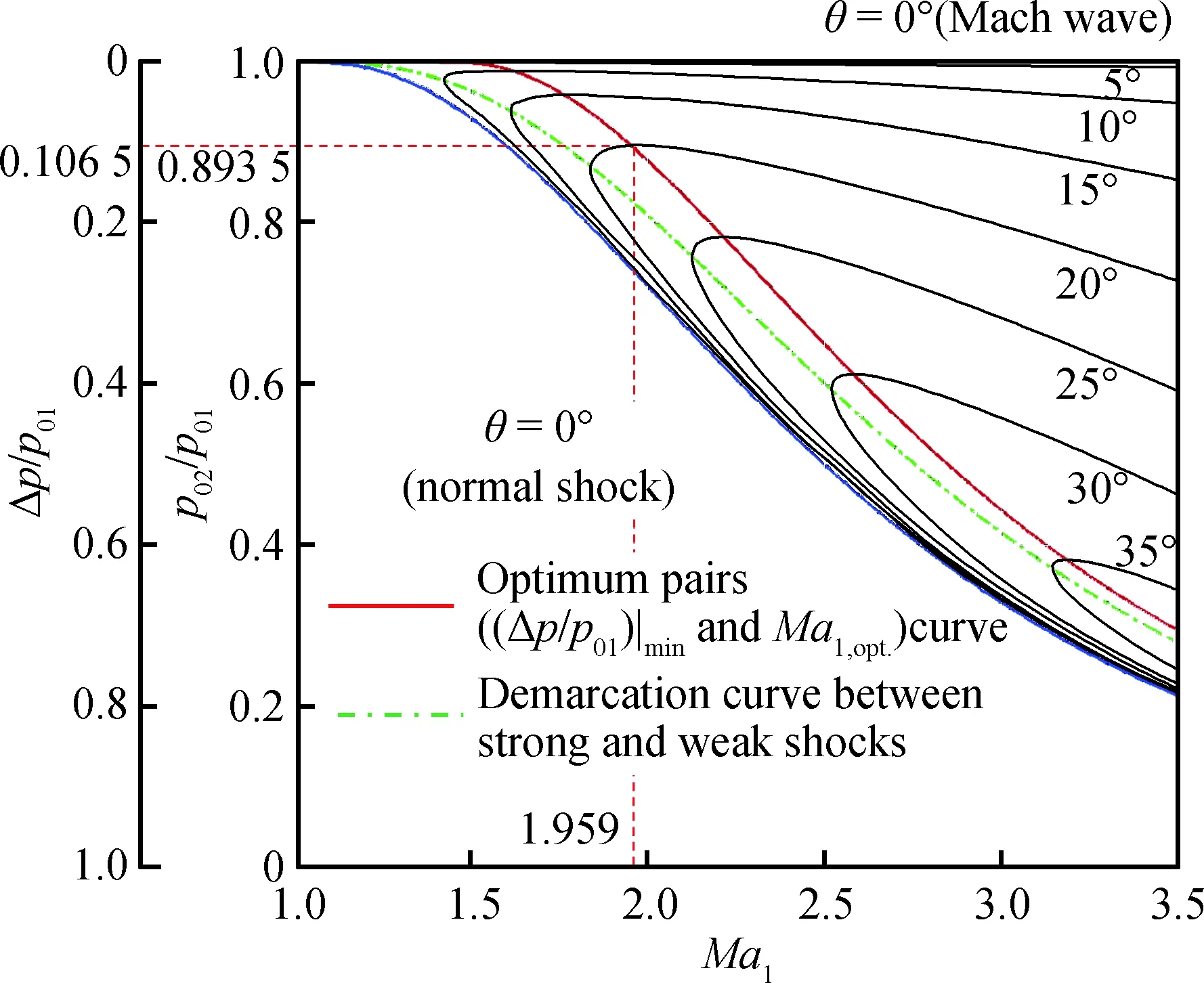
圖6 斜激波效率圖解法與總壓比數值法數據比對Fig.6 Comparison of data between oblique shock efficiency diagram solution and stagnation pressure ratio numerical method

關于研究方法，一個有趣的現象是：總壓比直接圖解法得到的最大總壓比數值形成的幾何圖形為曲線，不易被察覺；而斜激波圖解中得出的總壓損失率極小值線是直線，容易看出。第2節中θ-β-Ma*三維總壓損失率圖解分析也明確指出，總壓損失率函數極小值的三維空間曲線，僅在Oθβ投 影面上為直線且唯一。諸多因素也許是總壓損失率極小值線長久未被發現的原因。它的得到或有種“驀然回首、燈火闌珊”之感，但作者更愿意把“最小總壓損失律”的得出歸咎于氣動高效率超聲速飛行歷史發展的必然。作者與審稿人都期待總壓損失極小值控制方程與效率圖解能對生成高氣動效率的激波總壓理論產生積極意義，尤其是對從事激波有關的高速飛行器激波最小損失外流或進、排氣內流問題的研究者提供一個有益的理論啟示。

5 舉例應用

假設舉例應用如圖7所示。平面理想氣體中，小明駕駛一楔形角為20°的二維飛行器進行超聲速飛行。假設發動機具備提供任何飛行馬赫數的推進能力。小明的問題是選擇哪個飛行馬赫數檔位進行氣動效率最優的超聲速飛行。氣動效率最優意味著：在消耗相同油量的條件下，最優的超聲速飛行馬赫數將取得最大的飛行距離。小明的操作步驟是：① 運用式(3)算出最優激波角為55°；② 利 用式(2)和式(1)算出選擇最優飛行馬赫數為1.959；③ 通過式(5)得出儀表盤上顯示的空氣動力總壓利用率為89.35%。

如果還想進一步提高總壓利用率，小明將運用斜激波效率圖解(圖1)進行飛行器楔形角設計。從氣動效率考慮，小明是不會選擇效率圖解中區域②的馬赫數進行飛行的。總壓損失率相同，區域②中飛行馬赫數小于區域③中飛行馬赫數。區域②速度與效率都是低的。

利用相對運動原理，舉例說明可直接應用于與激波強度有關的二維超聲速流動問題中，可包括風洞試驗條件設定或計算標準模型設計等問題研究。如：激波/附面層干擾流動問題中，通過恰當組合物面楔形角和馬赫數來精確產生附面層入射激波需要的強度條件。

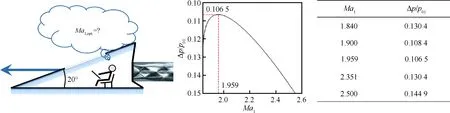
圖7 楔形角為20°的二維飛機選取平面超聲速流中最優飛行馬赫數的過程Fig.7 Process of two-dimensional aircraft with 20°wedge for selecting the optimal flight Mach number in a planar supersonic flow

6 結 論

1) 發現了蘊含于斜激波關系式中的總壓損失率極小值理論方程——僅為激波角和楔形角的直線方程。

2) 生成的斜激波氣動效率圖解便于超聲速激波結構總壓損失率規律的運用。

3) 解釋了完全對稱于總壓損失率極小值線的等值總壓損失率馬赫數與激波角的雙解特征。

致 謝

感謝Anderson教授(Andeerson教授為美國國家工程院院士，美國國家航空航天博物院空氣動力學館館長，馬里蘭大學榮譽教授)分享的Shapiro教授(Shapiro教授是美國國家科學院、工程院院士，麻省理工學院榮譽教授)撰寫麻省理工學院經典氣動著作中20°楔形角總壓比直接法圖解分析與數據驗證的研究思路。

感謝“可壓縮空氣動力學”核心課程教學團隊經常對教學問題的研討。感謝團隊首席宋文萍教授2015年課程全過程跟班教學培養。正是在跟班聽課中，作者再學習斜激波關系式并對氣動效率問題萌生疑問。感謝2016年選課同學王東璞和李民民課上、課下對開放問題的討論交流。

附錄A

將法向馬赫數Man1=Ma1sinβ代入斜激波關系式[1]，得

(A1)

(A2)

利用輔助角公式，化簡式(A2)，得

(A3)

式(A3)即為法向馬赫數表示的斜激波關系式。

由熵增總壓比關系式得總壓損失率公式為

(A4)

以Man1為自變量，對式(A4)求導，得

(A5)

由γ=1.4，Man1≥1，得(Δp/p01)′≥0；式(A4)是以Man1為自變量的單調增函數，得證。