基于非參數回歸改進的太湖總磷壓力響應模型

華祖林，韓愛秋

(1．河海大學淺水湖泊綜合治理與資源開發教育部重點實驗室，江蘇南京 210098;2．河海大學水資源高效利用與工程安全國家工程研究中心，江蘇南京 210098;3．河海大學環境學院，江蘇南京 210098)

湖泊參照狀態指湖泊受到人類活動影響最小或環境系統可達到的最佳狀態[1]，它是制定水質標準的科學依據，也是評估、預防、控制和管理湖泊富營養化的基礎，更是水污染治理和生態修復期望達到的“終極”狀態。壓力-響應模型是最適用于確定淺水湖泊參照狀態的模型之一。Lamon等[2]探索性地以貝葉斯多層次線性回歸模型確立了美國不同類型湖泊壓力變量和響應變量的響應關系;US EPA[3]介紹了利用線性回歸、多元線性回歸和非參數拐點分析等建立壓力-響應模型的方法;Haggard等[4]利用線性回歸和分類回歸樹相結合的方法確定了美國紅河流域的營養物基準值;Qian等[5]構建了連續變量貝葉斯網絡建模框架，該框架結合了貝葉斯網絡模型和傳統經驗統計模型，并確定了美國俄亥俄州溪流的營養物基準值;在中東部平原湖泊生態區、云貴高原湖泊生態區等8個湖泊營養物一級生態區的基礎上[6-7]，Huo等[8-11]引入壓力-響應模型來制訂中國受人類活動影響較嚴重湖泊的參照狀態，利用線性回歸壓力-響應模型制訂了東部平原湖泊生態區和云貴湖泊生態區的營養物基準，并在考慮季節影響水質的情況下采用分類回歸樹與拐點分析相結合的方法建立壓力-響應模型深入研究湖泊生態分區參照狀態的確定;吳超等[12]采用分類回歸樹和線性回歸分別建立了壓力-響應模型，并通過相互驗證確定了太湖TN、TP等的參照狀態;張亞麗等[13]利用貝葉斯拐點分析等3種非線性方法確定了中國9個典型湖泊的參照狀態;霍守亮等[14-15]利用分類回歸樹、拐點分析法、貝葉斯層次線性回歸建立了壓力-響應模型，針對不同湖泊生態分區進行參照狀態的確定和案例研究，并進行了歸納總結。

以上研究成果有值得商榷和改進之處，如線性回歸模型要求響應關系是線性的、因變量的誤差呈正態分布、采集的數據樣本獨立等，而實際上，光照、水深等環境因素會影響變量間的響應關系，導致其難以呈現出線性;此外，湖泊實際監測數據來源復雜，且為時間序列，很難滿足線性回歸分析設定的正態性和獨立性等假設理論。貝葉斯層次回歸模型雖然能有效緩解數據測量誤差的問題，但需要在調查時以明顯分層的方式采集原始數據，以便分層建立模型。分類回歸樹壓力-響應模型適用于識別對模型結果變化有顯著貢獻的壓力變量，但在數據量較少時缺乏穩健性，壓力變量很小的變化可能引起模型結果較大的變化，使結果的準確性得不到保障;拐點分析法需要進一步研究低于營養物拐點對應的響應變量數值是否能夠支持水體的指定用途[14-15]。這些限制性條件會導致推斷的參照狀態濃度過高或過低。壓力-響應模型方法的改進一直是學者們孜孜不倦探索的課題。

本文針對原有壓力-響應模型需要滿足設定條件等特點，考慮到響應關系應是非線性的，以及異常點會降低模型穩健性等情況，嘗試性地采用非參數LOWESS穩健回歸來改進淺水湖泊的壓力-響應模型。改進模型能消除異常點對估計結果的影響，對于非線性、非齊次問題有較好的效果。太湖作為東部平原湖泊生態區淺水湖泊的典型代表，參照狀態的確定尤為重要[16-17]，以太湖為研究對象進行湖泊參照狀態的確定計算。

1 非參數LOWESS穩健回歸模型的構建

非參數LOWESS穩健回歸是擬合難以用具體函數描述響應關系數據的有效方法，其基本思想是先用局部多項式進行擬合，然后定義穩健的權數并進行光滑處理，重復運算數次后就可以得到自變量與因變量穩健的擬合曲線[18]。具體步驟如下：

步驟1：將壓力變量TP和響應變量Chl-a關系曲線表示為m(x)，利用局部多項式進行擬合，得到擬合值 ^m(xi)：

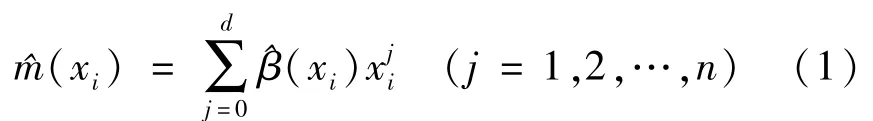
式中：xi為TP的觀測值，mg/L;β^(xi)為對局部參數β(xi)的最小二乘加權回歸。

步驟2：定義并計算穩健權數δk：

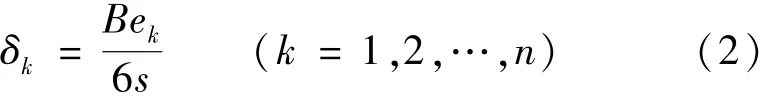
其中 ek=m(xk)-m^(xk)

式中：B為二次核函數，定義為B(x)=(1-x2)2I(I為符號函數，當|x|＜1時I=1;當|x|≥1時I=0);ek為殘差;xk為加權的xi;s為殘差絕對值的中位數，s=median(e1， e2，…， en)。

步驟3：利用δkwk(xi)對m(x)進行局部加權最小二乘估計，得到新的模型殘差ek。其中

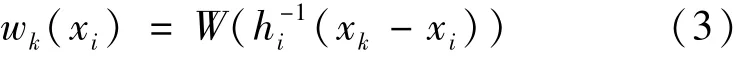
式中：W為距離權函數;hi為光滑參數，hi= xi-xj，xj(j=1，2，…，n)為 xi相鄰的 TP 觀測值，hi為計算得出的r個數中最小的一個。

步驟4：重復第2步和第3步，最后第N次迭代得到的擬合值產生TP和Chl-a的響應關系曲線。

穩健權數可將異常值排除在外，并且初始殘差大(小)的觀測值在下一次加權最小二乘法中的權數就小(大)，重復幾次后就可把異常值不斷地排除在外，最終得到穩健的響應關系曲線。Cleveland[18]推薦迭代次數N=3。

非參數LOWESS穩健回歸壓力-響應模型構建流程見圖1。

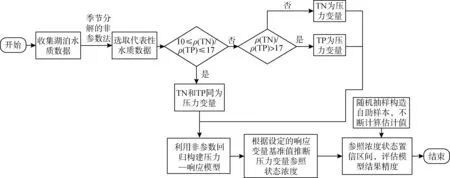
圖1 壓力-響應模型構建流程

2 模型數據與壓力變量的確定

2.1 模型數據

利用LOWESS穩健回歸方法建立壓力-響應模型推斷太湖參照狀態，數據來源于文獻[19]。文獻[19]記錄了圖2太湖湖泊生態系統國家野外科學觀測研究站(簡稱太湖站)全太湖32個野外站點中8個站點自1991—2006年的逐月觀測數據。考慮到參照狀態是受人類活動影響最小或環境系統可達到的最佳狀態，所以本文采用位于湖心區域受人類活動影響相對較小的7號和8號站點的數據。華祖林等[20]采用季節分解的非參數法發現1999—2001年太湖湖心區域的TP與Chl-a的觀測值比1995—2006年的觀測值更適合用于推斷太湖的參照狀態。本文使用7、8號站點1999—2001年共3年108個觀測值進行分析。

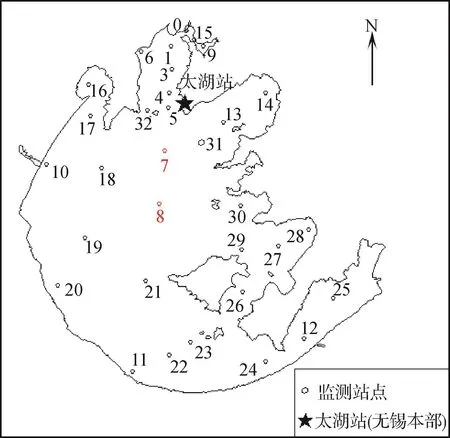
圖2 太湖站監測點圖

2.2 壓力變量確定和數據處理

首先對模型數據進行分析。1999—2001年，太湖湖心TN、TP以及Chl-a質量濃度平均值、中位數、均方差等見表1。1999—2001年太湖湖心觀測值穩定性按從大到小順序為TP、TN、Chl-a。在峰度和偏度檢驗中，TN、TP和Chl-a均存在正偏態現象，偏重程度按從大到小順序為Chl-a、TN、TP，且三者均偏離正態分布。綜合考慮數據穩定性及峰度和偏度檢驗結果，在選擇壓力變量時應優先考慮TP。

在研究湖泊氮磷與Chl-a關系時，TN與TP質量濃度比值(ρ(TN)/ρ(TP))是一個關鍵參數，常根據ρ(TN)/ρ(TP)判別藻類受營養鹽限制的類型。ρ(TN)/ρ(TP)比較大(＞17)時藻類受磷限制，ρ(TN)/ρ(TP)比較小( ＜10)時藻類受氮限制，ρ(TN)/ρ(TP)中等(10～17)時藻類受二者共同限制。表1顯示太湖1999—2001年TN質量濃度平均值為1．69 mg/L，TP 質量濃度平均值為 0．08 mg/L，ρ(TN)/ρ(TP)=21．12，大于 17。 可見，1999—2001年太湖為磷限制型湖泊。張波等[21]研究表明，太湖水體存在一定的固氮作用，固氮速率為每小時1．53 ng/L，導致水體中TN與Chl-a響應關系不明顯。因此分析太湖TP和Chl-a的響應關系更符合壓力-響應模型的釋義。

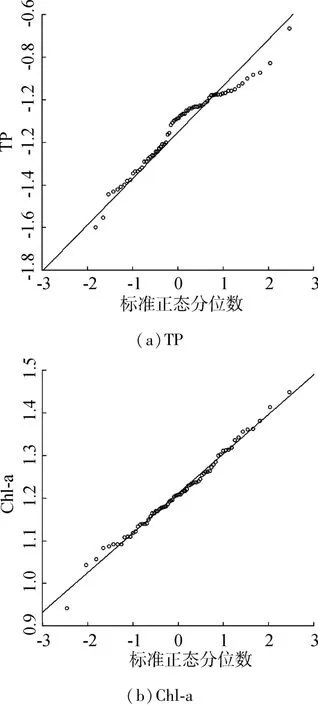
圖3 TP與Chl-a冪變換數據Q-Q圖

表1 1999—2001年TN、TP與Chl-a統計特征比較

由于原始逐月觀測數據TP與Chl-a存在數量級差別，因此需要對原始數據進行處理。本文采用Qian[22]提出的冪變換對TP和Chl-a數據進行處理。圖3是TP數據經過對數變換后和Chl-a 0．1次方變化后的Q Q圖。從圖3可以明顯地看出，TP數據點與標準正態分布直線擬合效果較差，存在嚴重的偏離。結合表1峰度和偏度檢驗結果，說明1999—2001年太湖湖心TP觀測數據和冪變換后均不滿足正態性假設，所以基于上述假設建立的壓力-響應模型具有不合理性，進一步說明建立非參數方法壓力-響應模型的必要性。

在采用壓力-響應模型推斷參照狀態時，需要給定一個響應變量基準值。在保證水體使用功能的前提下推斷營養物基準時，Chl-a是聯系營養物濃度的重要響應變量[8]。參考 USEPA[23]和霍守亮等[14，24-25]對Chl-a基準值的研究，本文在建立壓力-響應模型時設定4．73 μg/L Chl-a為太湖響應變量基準值。

3 模型驗證

采用LOWESS穩健回歸建立1999—2001年太湖湖心區域TP與Chl-a的壓力-響應模型，平滑參數f=0．2，迭代次數 N=3。圖4為太湖湖心區域1999—2001年Chl-a與TP壓力-響應模型及模型殘差。從圖4的散點可以看出，Chl-a與TP并不呈現出簡單的線性響應關系，而是復雜的非線性響應關系。根據確定的響應變量Chl-a基準值4．73 μg/L，可以得出壓力變量TP的參照狀態質量濃度為0．018 mg/L。此外，結合置信區間和模型殘差評估模型結果的準確性，利用自助法求得1999—2001年太湖TP參照狀態質量濃度的95%置信區間為0．013～0．030 mg/L。 從圖4(b)可以看出，模型殘差均值為0．0mg/L左右，下25%分位點為-0．06 mg/L，上25%分位點為0．04mg/L，說明LOWESS穩健回歸方法可用于建立壓力-響應模型進行參照狀態的推斷。

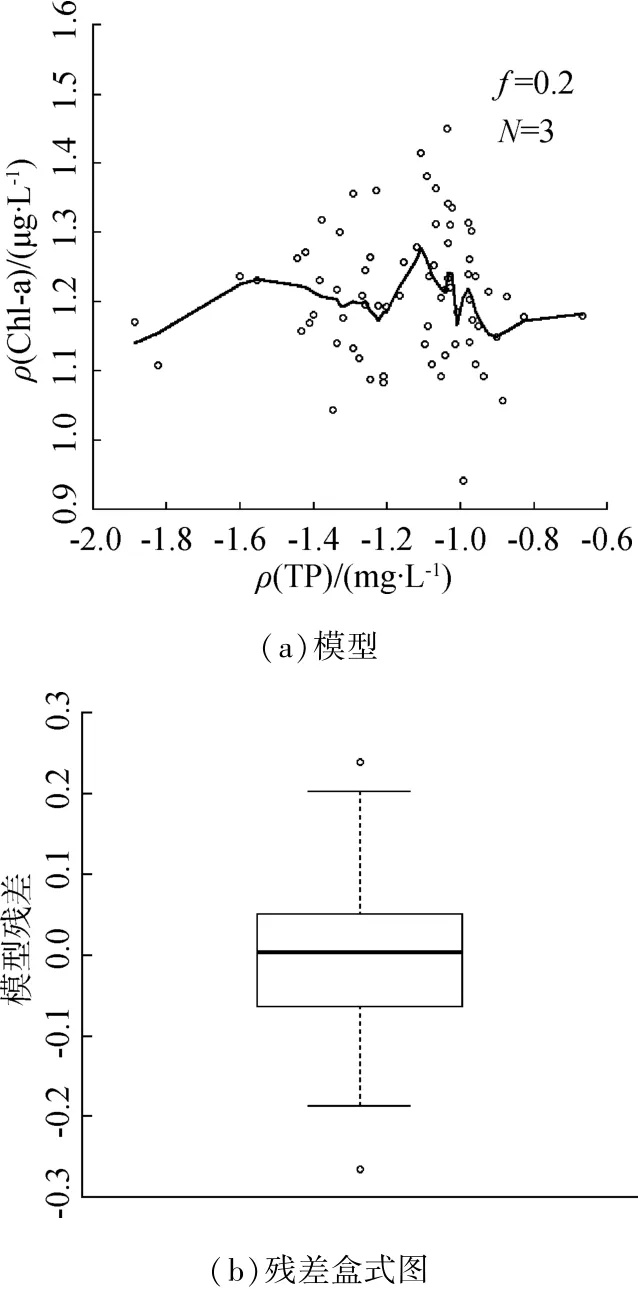
圖4 TP與Chl-a壓力-響應模型及模型殘差

表2顯示的是不同地區TP參照狀態質量濃度。鄭丙輝等[26]應用頻率分析法建立了太湖TP參照狀態，并結合時間參照狀態法和沉積物反演法進行驗證，綜合分析得出TP參照狀態為0．03 mg/L;華祖林等[20]利用1999—2001年TP數據5%分位點的值作為太湖參照狀態質量濃度，其結果為0．03 mg/L，并利用幾何分布分塊自助法確定其95%置信區間為0．025～0．046 mg/L。采用頻率分析法在確立湖泊參照狀態時需要確定頻率分布分位點，通常都是選擇上(下)25%或5%，由于25%或5%是人為確定的，因而結果受到人為影響大。吳超等[12]利用分類回歸樹和線性回歸法建立的壓力-響應模型相互驗證，確定太湖流域TP質量濃度基準值為0．67mg/L。

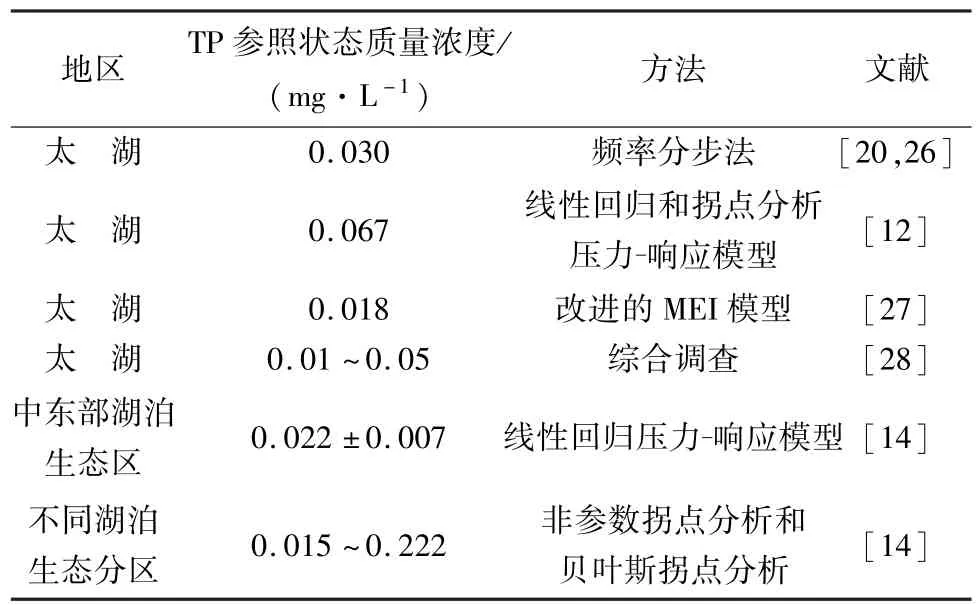
表2 不同地區TP參照狀態濃度

霍守亮等[14]利用非參數拐點分析和貝葉斯拐點分析，得到不同湖泊生態區壓力變量TP突變點的質量濃度范圍為0．015～0．222mg/L，利用簡單線性回歸模型得到中東部湖泊生態分區TP參照狀態質量濃度范圍為(0．022±0．007)mg/L;顧莉等[27]將1960年總堿度實測值代入其建立的改進MEI模型得到太湖TP質量濃度為0．018mg/L。在20世紀60年代對太湖的調查研究表明，太湖TP質量濃度為0．01～0．05 mg/L[28]。 太湖藍藻暴發最近30年才出現，60年代太湖的狀態應該比較接近其歷史上受人類活動影響較小時的情況。本文采用季節分解的非參數局部線性回歸模型推斷得出更適合建立太湖參照狀態的數據，而且非參數LOWESS穩健回歸不需要設定分位點，計算過程受人為影響小，計算得到的太湖TP參照狀態質量濃度為0．018 mg/L，在線性回歸和拐點方法得出的參照狀態質量濃度范圍內。因此，本文得到的結果可以作為太湖參照狀態質量濃度，并且是可信的。

4 結 語

以季節分解的非參數方法驗證的適合推斷太湖參照狀態的數據為基礎，結合峰度和偏度檢驗，并考慮湖泊營養鹽的限制問題，以TP作為壓力變量，構建了穩健性高、對非線性問題適應性強的LOWESS穩健回歸的湖泊壓力-響應模型。根據設定的Chl-a推斷TP的參照狀態質量濃度為0．018 mg/L;通過自助法得出其95%置信區間為0．013～0．030 mg/L，同時從多角度對所建模型進行了驗證，表明結果較為合理可信。