THE COMPUTING FORMULA FOR TWO CLASSES OF GENERALIZED EULER FUNCTIONS
LIAO Qun-ying,LUO Wen-li
(1.College of Mathematics,Sichuan Normal University,Chengdu 610066,China)
(2.The Middle School Attached to Sichuan University(No.12 Middle School),Chengdu 610061,China)
Abstract:In this paper,we study the computing formula of the generalized Euler function.By using elementary methods and techniques,we obtain the computing formula of the generalized Euler function ?pq(n)for some cases and the computing formula of ?e(n)(e=p,p2)for any prime factor m|nwith m≡1 or?1(mod e)and gcd(m,e)=1,where pand qare distinct primes,which are the generalizations for the corresponding main results given in[5].
Keywords:Euler function;generalized Euler function;Mbius function
1 Introduction
In 18th century,as one of the most outstanding mathematician,Euler first defined the Euler function?(n)of a positive integernto be the number of positive integers not greater thannbut prime ton[1].It’s well known that as one of the important number theory functions,Euler function was applied widely.Euler function played a key role in RSA public-key cryptosystem since 1970’s,and it is also one of the important tools to seek the theoretical basis for the generators of circle groups.There were many interesting open problems on Euler function[2].For example,Carmichael conjectured that for any positive integern,there exists a positive integermsuch thatm 6=nand?(m)=?(n).And then Schinzel conjectured that for any fixed positive integerk,the equation?(n+k)=?(n)has infinitely many positive integer solutions forn.
On the other hand,in 1938,for any odd primep,Lehmer[3]established the following important congruence identity
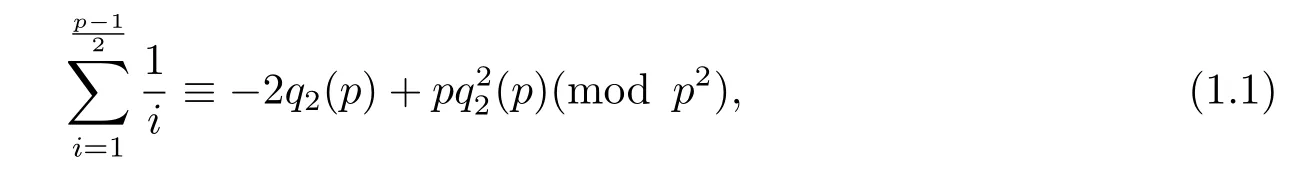
whereqr(n)denotes the Euler quotient,i.e.,,nandr≥2 are both natural numbers with gcd(n,r)=1.
By using(1.1)and the others similar congruences identity,Lehmer obtained many ways to prove the first case of the well-known Fermat’s last theorem[4].Until 2002 and 2007,basing on(1.1)and the other congruence identities given by Lehmer,Cai,etc[5,6]generalized the modulo from the square of a prime to the square of any positive integer,and defined the generalized Euler function for any positive integernto be
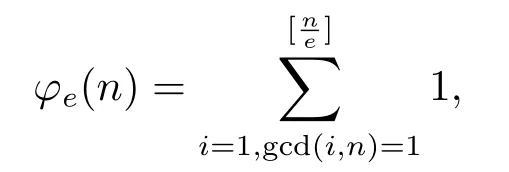
i.e.,?e(n)is the number of positive integers not greater thanbut prime ton,whereeis a positive integer and[x]is the greatest integer which is not greater thanx.It’s easy to verify that?1(n)=?(n)is the known Euler function ofn,and

whereμ(n)is the Mbius function,i.e.,
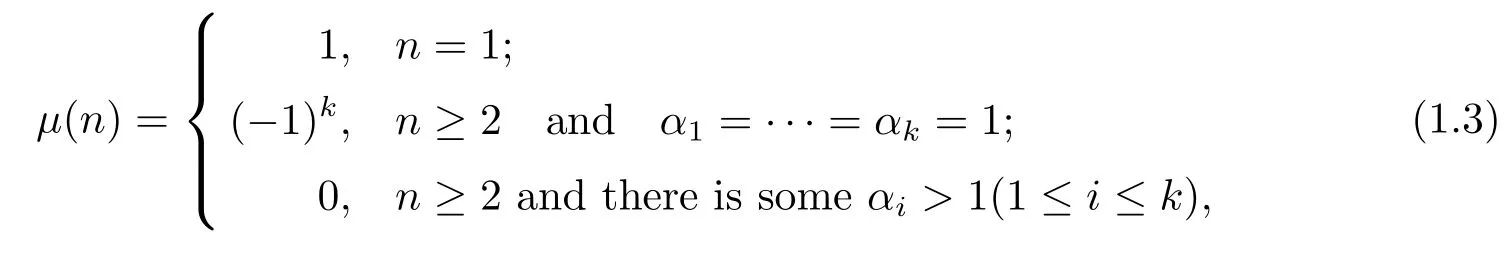

On the other hand,fore=1,the following computing formula for the generalized Euler function is well-known
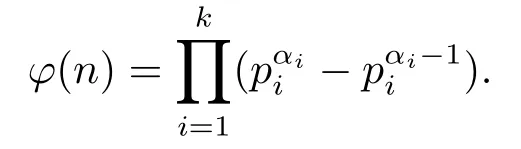
Therefore one can naturally to ask the following
QuestionFor any fixed positive integere,determine the explicit algorithm formula for the generalized Euler function?e(n).
In recent years,Cai etc[7,8]obtained the accurate calculation formula for?e(n)(e=2,3,4,6),and then,by using properties for Legendre or Jacobi symbols,they also got some necessary and sufficient conditions for that?e(n)and?e(n+1)(e=2,3,4)are both odd or even numbers.
Proposition 1.1[7,8]Letp1,···,pkbe distinct primes,α1,···,αkbe positive integers,and.
(1) If gcd(pi,3)=1(i=1,···,k)andn=3αn1>3,then
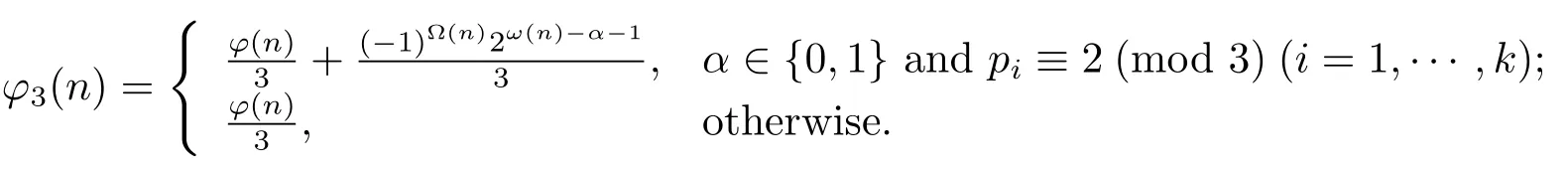
(2) Ifαis a nonnegative integer andn=2αn1>4,then
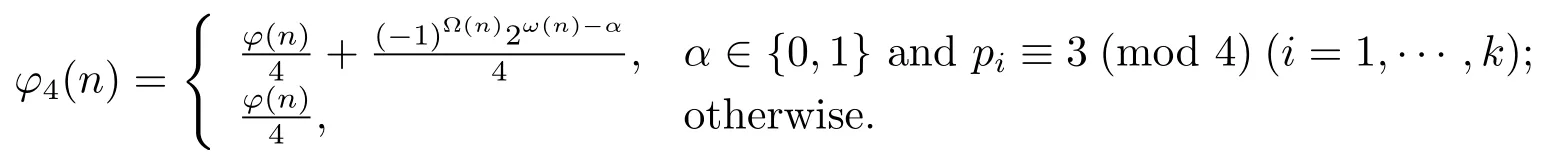
(3) If gcd(pi,6)=1(i=1,···,k)andn=2α3βn1>6,then
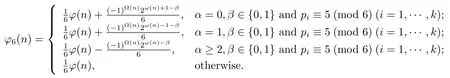
Recently,we[9]obtained the formula for?5(n)and some sufficient conditions for 2|?5(n).The present paper continues the study,based on the elementary methods and techniques,the computing formula for?e(n)(e=p,p2,pq)is obtained,wherepandqare distinct primes(Theorems 1.1–1.5).
For convenience,throughout the paper,we assume thatp,q,p1,···,pkare distinct primes,α1,···,αkare positive integers,αandβare both nonnegative integers,and
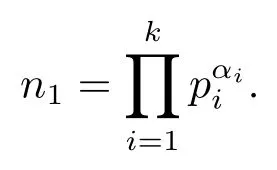
Theorem 1.1Ifn=pαn1>p,then
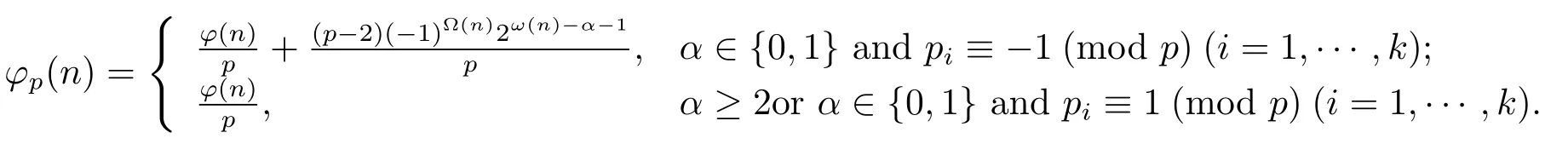
Theorem 1.2Ifn=pαn1>p2,then
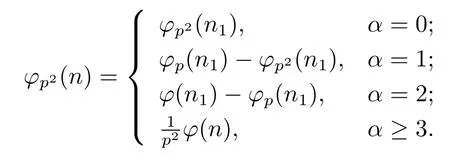
Theorem 1.3Forn=pαn1>p2andα≤2.
(1) Ifα=0,then
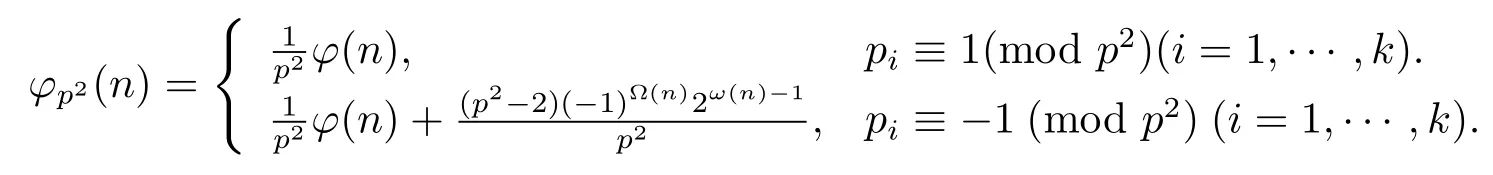
(2) Ifα=1,then
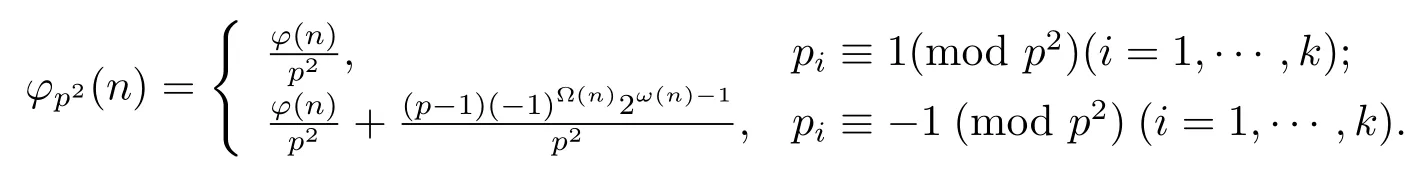
(3) Ifα=2,then
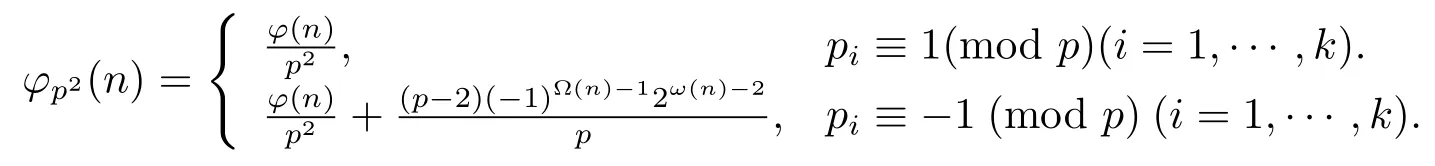
Theorem 1.4Ifn=pαqβn1>pq,then
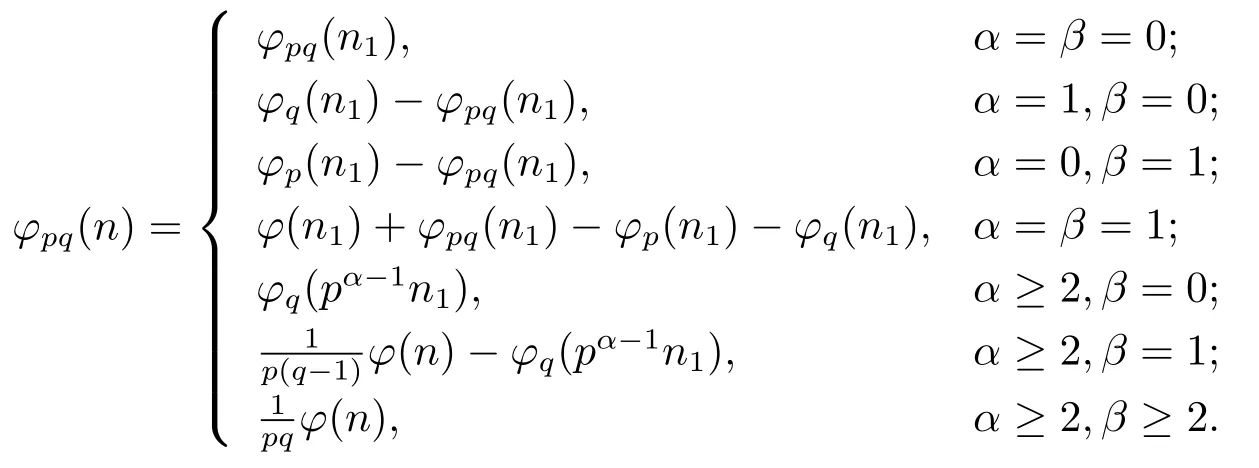
Theorem 1.5Forn=pαqβn1>pq.
(1) Ifα=β=0,then
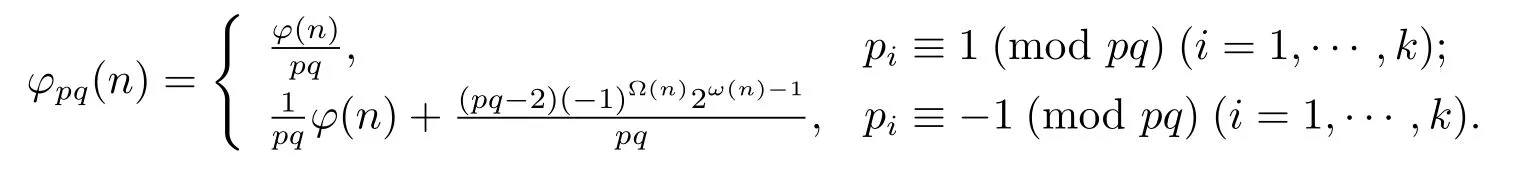
(2) Ifα=1 andβ=0,then
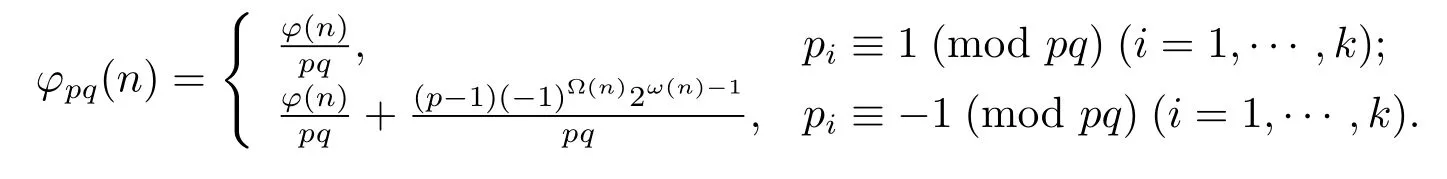
(3) Ifα=0 andβ=1,then
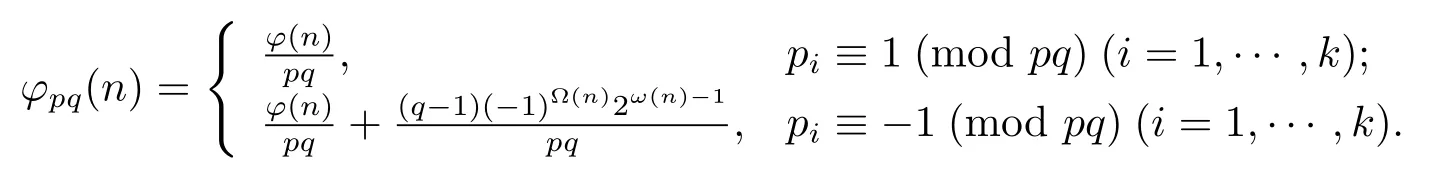
(4) Ifα=β=1,then
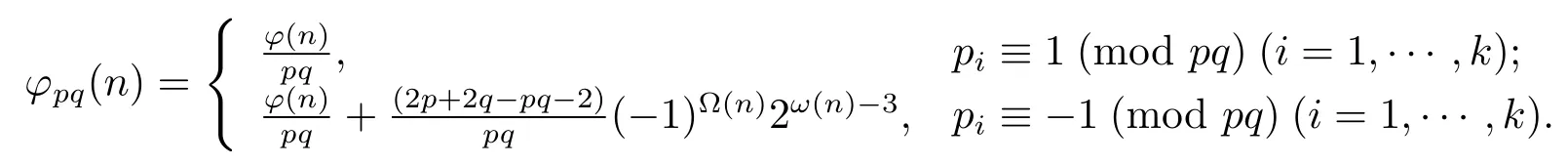
(5) Ifα≥2 andβ=0,then
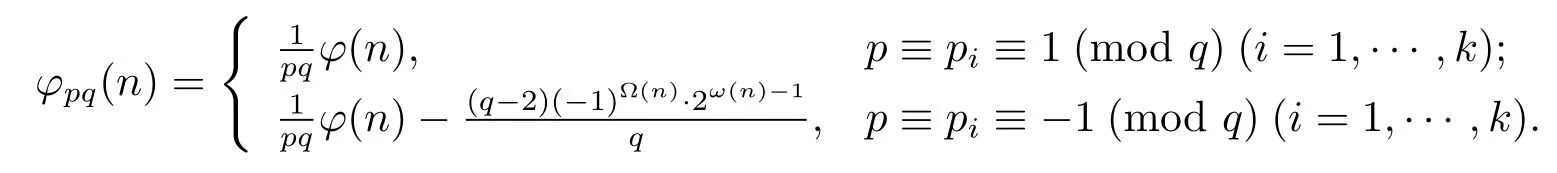
(6) Ifα≥2 andβ=1,then
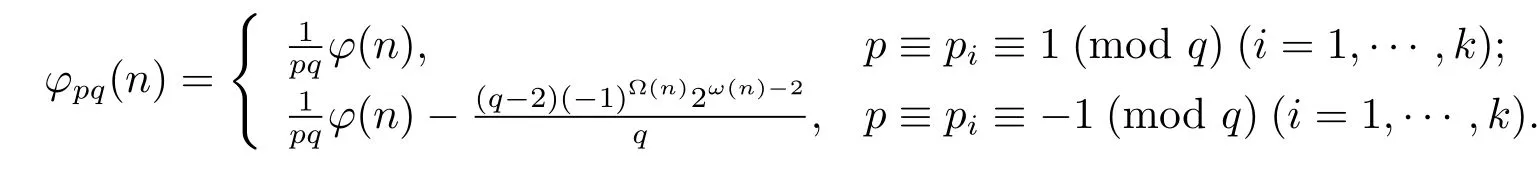
(7) Ifβ≥2 andα∈{0,1},then
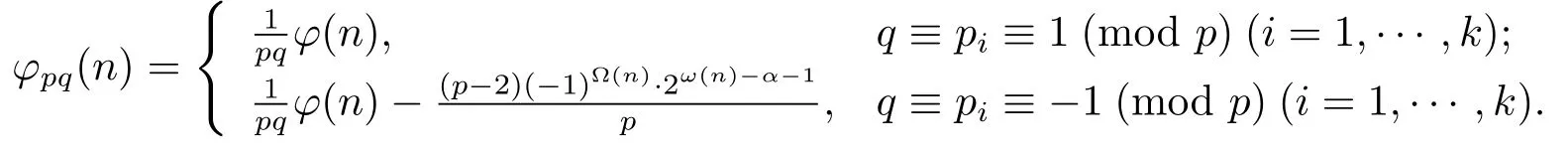
RemarkBy takingp=3 in Theorem 1.1,orp=2 in Theorems 1.2–1.3,one can get(1)or(2)of Proposition 1.1,respectively.And by takingp=2 andq=3 in Theorems 1.4–1.5,one can get(3)of Proposition 1.1.The details is left to interested readers.
2 Proofs for Main Results
Proof for Theorem 1.1(1) Ifα=0 andpi≡?1(modp)(i=1,···,k),i.e.,n=n1and for anyd|n1,d≡±1(modp).Then by(1.2)–(1.4),we have

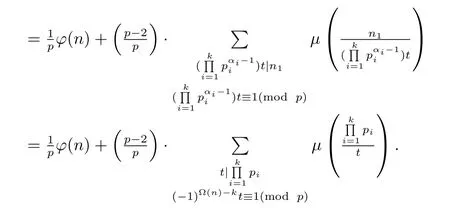
(a) If 2|?(n)and 2|k,then by(2.1)andn=n1,we have ?(n)= ?(n1),ω(n)=ω(n1)and
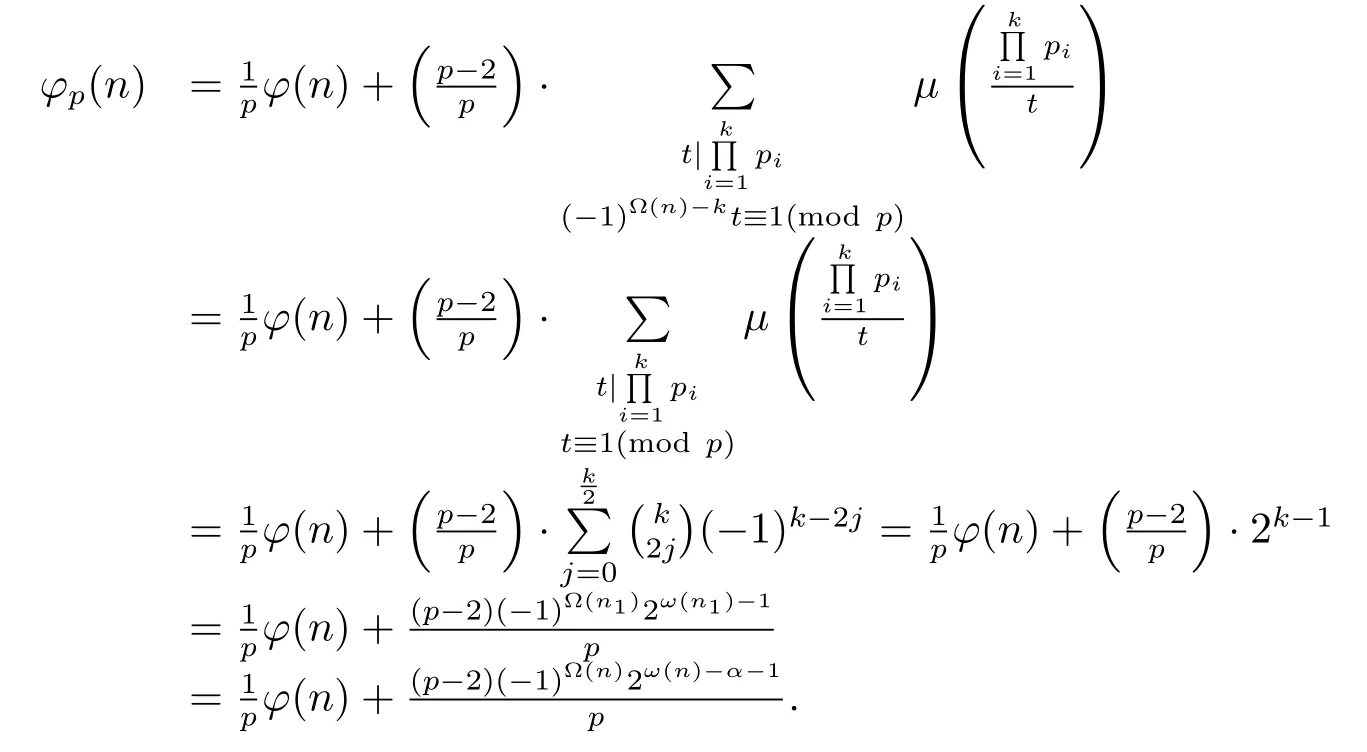
(b) If 2|?(n)and 2-k,then by(2.1)we have
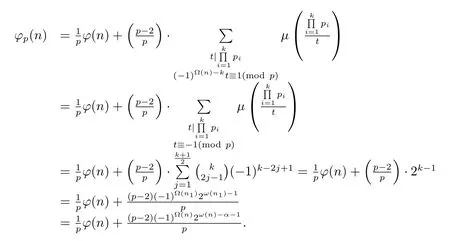
For the case 2-?(n)and 2-kor 2-?(n)and 2|k,in the same proof,we can get
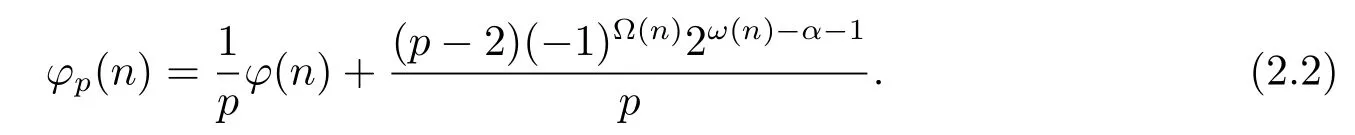
(2) Ifα=1 and for anyi=1,···,k,pi≡?1(modp),i.e.,n=pn1and for anyd|n1,d≡±1(modp).Then by(1.2)–(1.3),(2.2)and gcd(p,n1)=1,we have
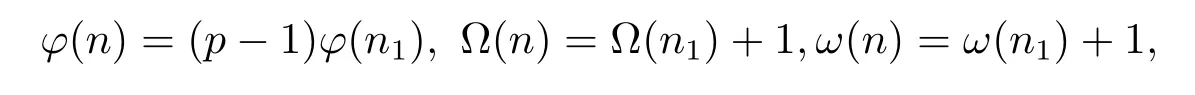
and then
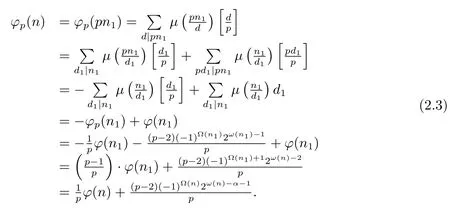
(3) Ifα≥2,i.e.,n=pαn1,then by gcd(p,n1)=1 and(1.2)–(1.3),we have
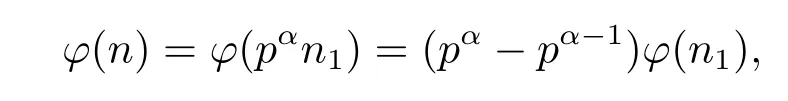
and then
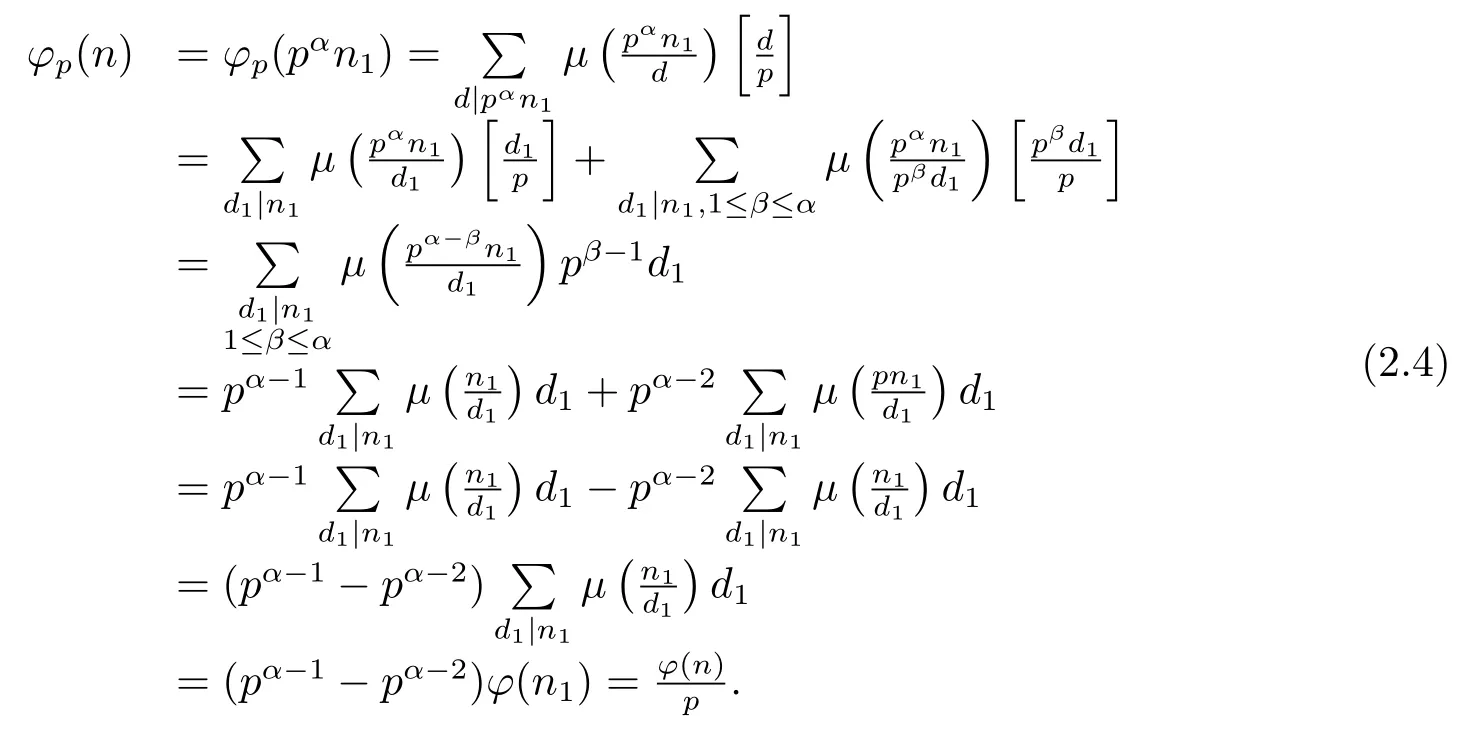
(4) Ifα=0 andpi≡1(modp)(i=1,···,k),i.e.,n=n1and for anyd|n1,d≡1(modp).Then by(1.2)and(1.4),we have
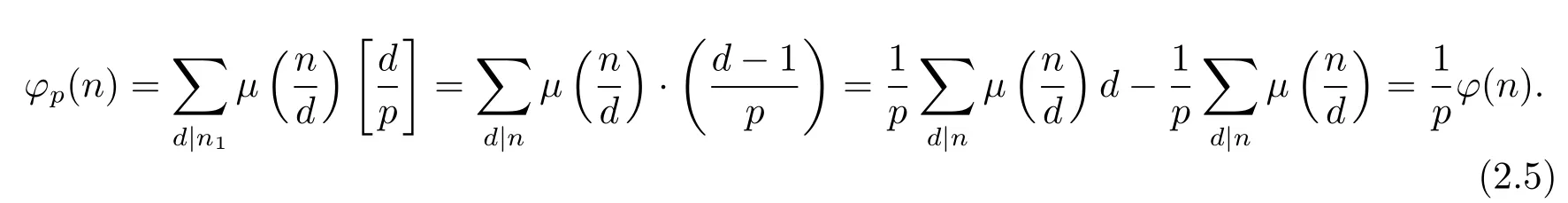
(5) Ifα=1 andpi≡1(modp)(i=1,···,k),i.e.,n=pn1,then?(n)=(p?1)?(n1)and for anyd|n1,d≡1(modp).Thus by(1.2)–(1.3),gcd(p,n1)=1 and(4)we have
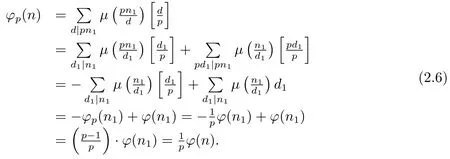
Now from(2.2)–(2.6),Theorem 1.1 is proved.
Proof for Theorem 1.2(1) For the caseα=0,the result is obvious.
(2) Ifα=1,i.e.,n=pn1,then by gcd(p,n1)=1 and(1.2)–(1.3),we have

(3) Ifα=2,i.e.,n=p2n1,then by gcd(p,n1)=1 and(1.2)–(1.3),we have
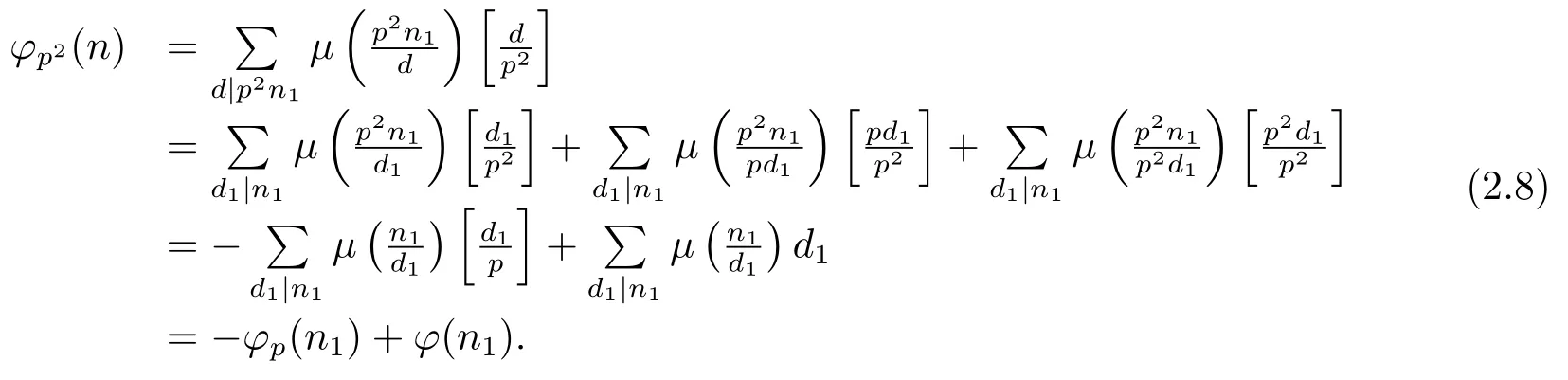
(4) Ifα≥3,i.e.,n=pαn1,then by gcd(p,n1)=1 and(1.2)–(1.3),we have?(n)=p2(pα?2?pα?3)?(n1),and then
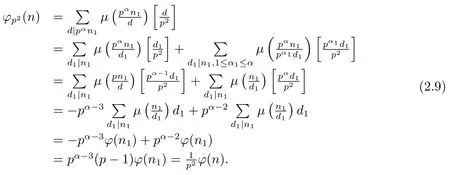
Now from(2.7)–(2.9),we complete the proof of Theorem 1.2.
Proof for Theorem 1.3(1) Ifα=0,i.e.,n=n1,and then gcd(n,p)=1.Suppose thatpi≡1(modp2)(i=1,···,k),then for anyd|n,d≡1(modp2),thus by(1.2)–(1.4),we have
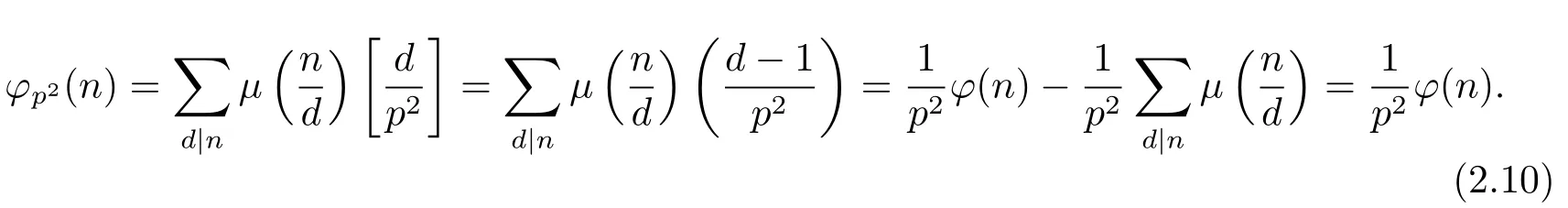
Suppose thatpi≡?1(modp2)(i=1,···,k),i.e,for anyd|n,d≡±1(modp2),and then by(1.2),(1.4)and the proof of Theorem 1.1(1),we can get
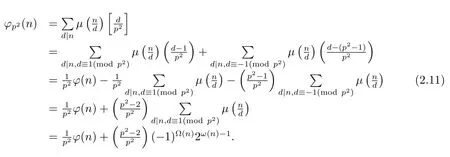
Now from(2.10)–(2.11),we complete the proof of(1).
(2) Ifα=1,i.e,n=pn1,then by gcd(p,n1)=1,we have
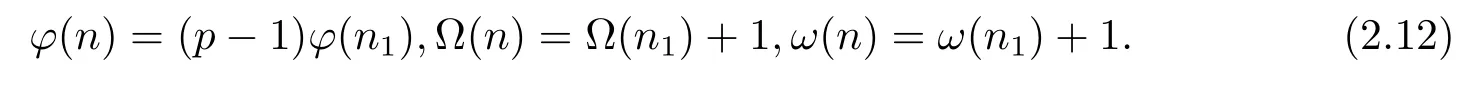
And so by Theorems 1.1–1.2,(2.12)and(1),we can obtain
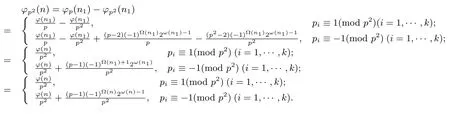
This completes the proof of(2).
(3) Ifα=2,i.e,n=p2n1,then by gcd(p,n1)=1,we have
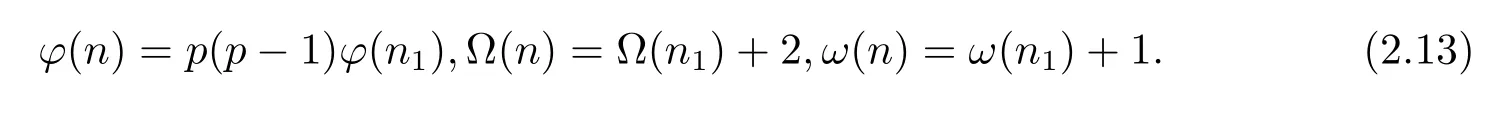
Thus by Theorems 1.1–1.2 and(2.13),in the same proof as that of Theorem 1.3(2),(3)is immediate.
This completes the proof of Theorem 1.3.
Proof for Theorem 1.4(1) Ifα=0,β=0,the result is obvious.
(2) Ifα=1,β=0,i.e.,n=pn1,then by gcd(pq,n1)=gcd(p,q)=1 and(1.2)–(1.3),we have
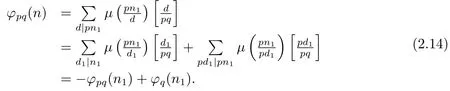
(3) For the caseα=1,β=0,in the same proof of(2),the result is obvious.
(4) Ifα=β=1,i.e.,n=pqn1,then by gcd(pq,n1)=gcd(p,q)=1 and(1.2)–(1.3),in the same proof as that of(2),(4)is immediate.
(5) Ifα≥2 andβ=0,i.e.,n=pαn1,then by gcd(p,n1)=1 and(1.2)–(1.3),we can obtain
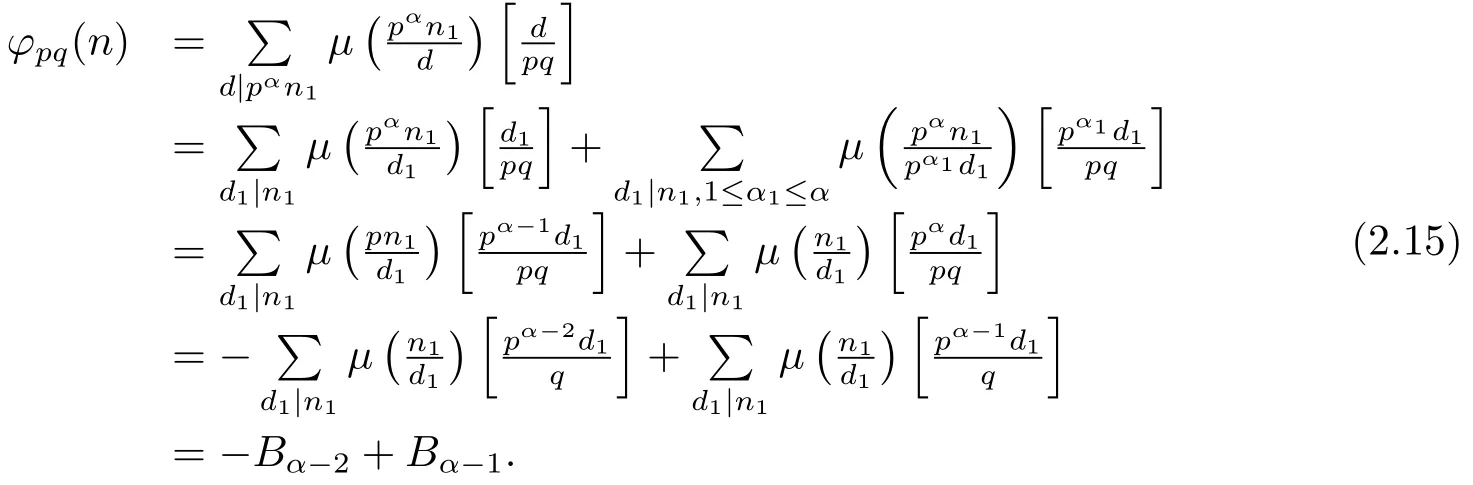
While byα≥2 and(1.2)–(1.4),we know that
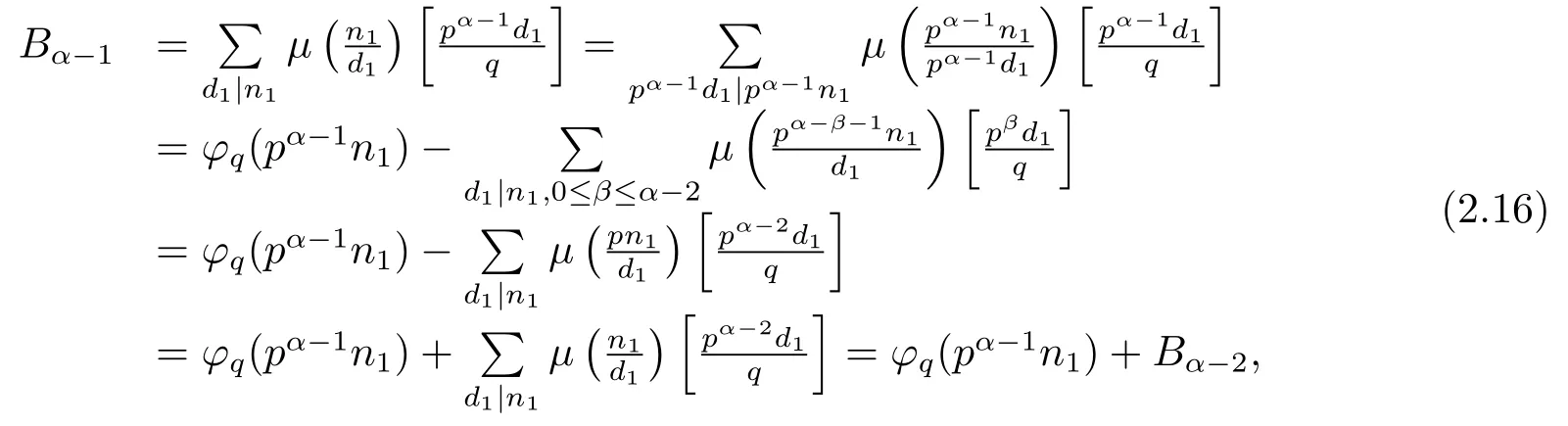
thus by(2.15)–(2.16),we have?pq(n)=?q(pα?1n1).Thus(5)is proved.
(6) Ifα≥2 andβ=1,i.e.,n=pαqn1,then by gcd(p,n1)=1,we have
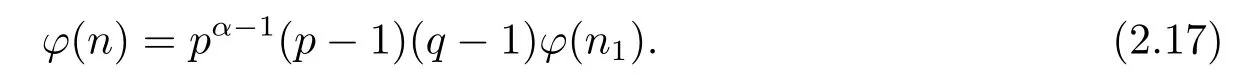
Thus by(1.2)–(1.4),(2.16)and(2.17),we can get
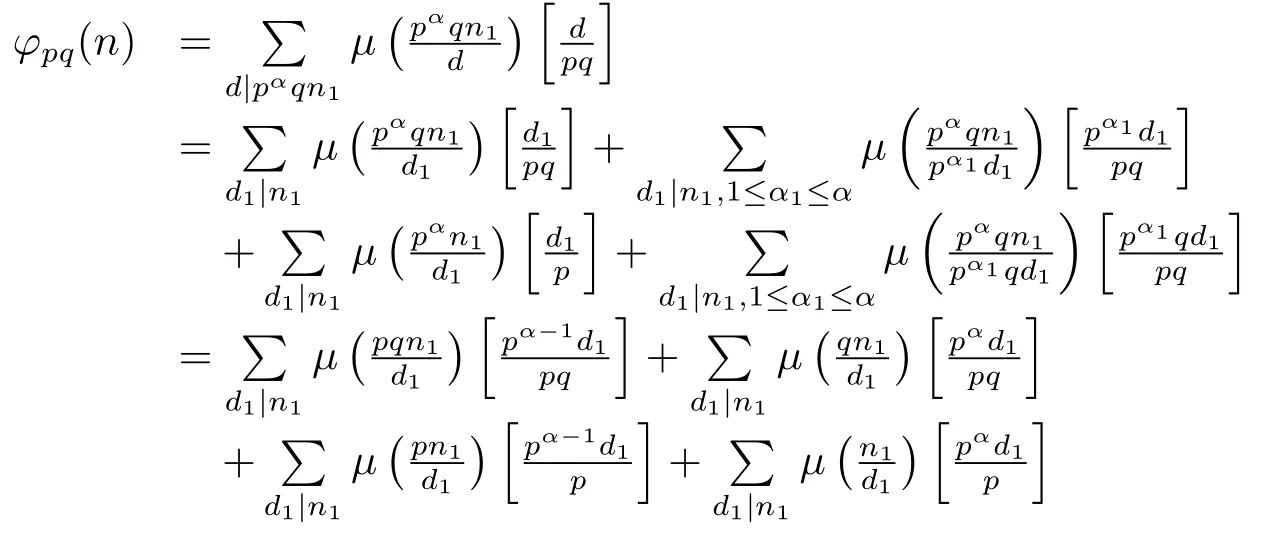
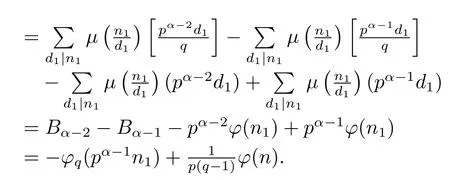
(7) Ifα≥2 andβ≥2,then by gcd(pq,n1)=gcd(p,q)=1,and(1.2)–(1.4),we have
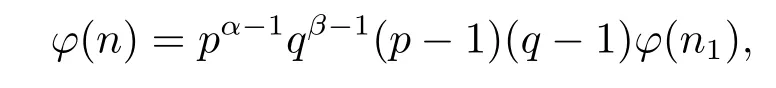
and then
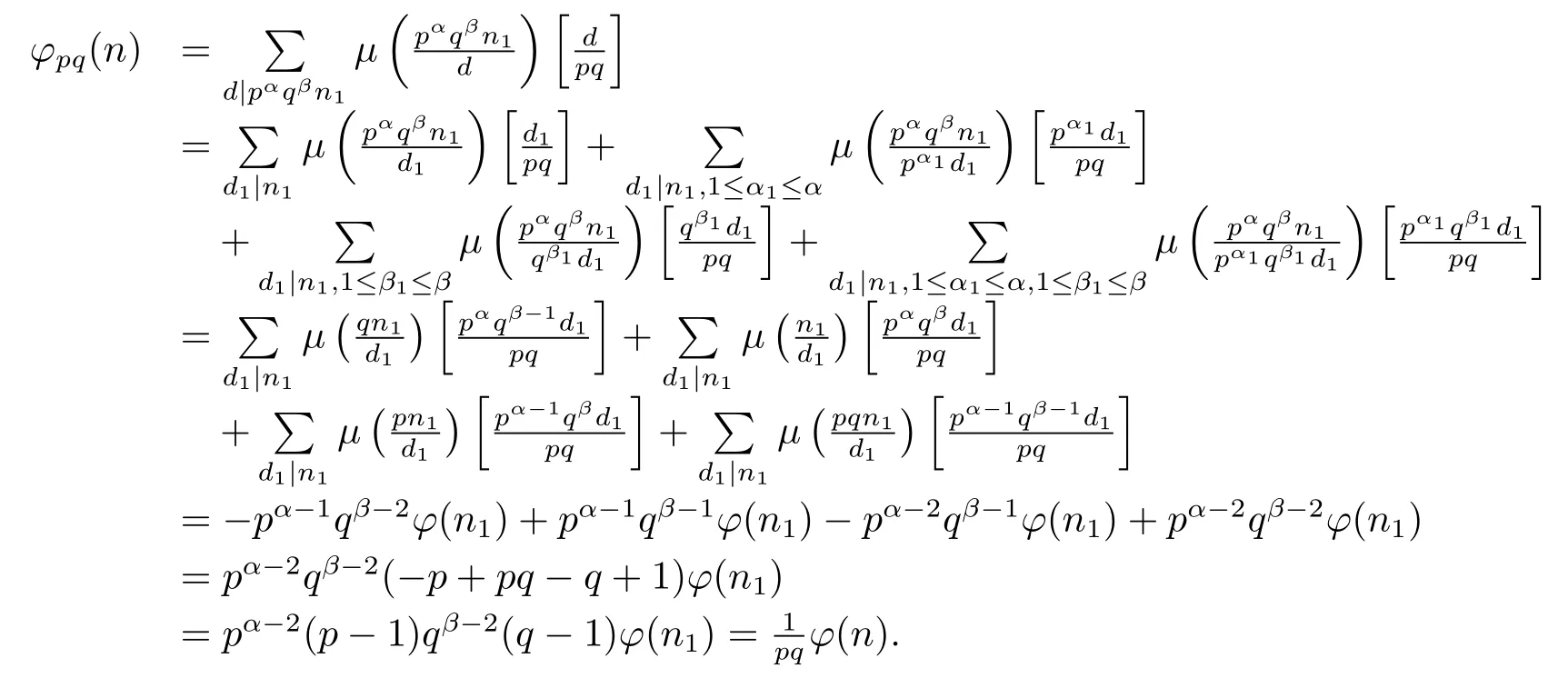
This completes the proof of(7).
Proof for Theorem 1.5(1) For the caseα=β=0,i.e.,n=n1.
(i) Ifpi≡1(modpq)(i=1,···,k),then for anyd|n,d≡1(modpq).Thus by(1.2)and(1.4),we have
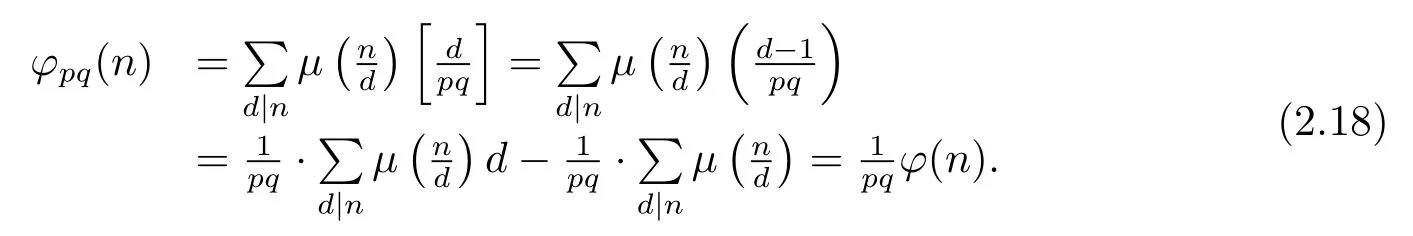
(ii) Ifpi≡?1(modpq)(i=1,···,k),i.e.,for anyd|n,d≡±1(modpq).Then by(1.2)–(1.4)and the proof of Theorem 1.1(1),we have
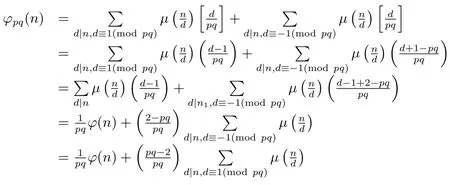
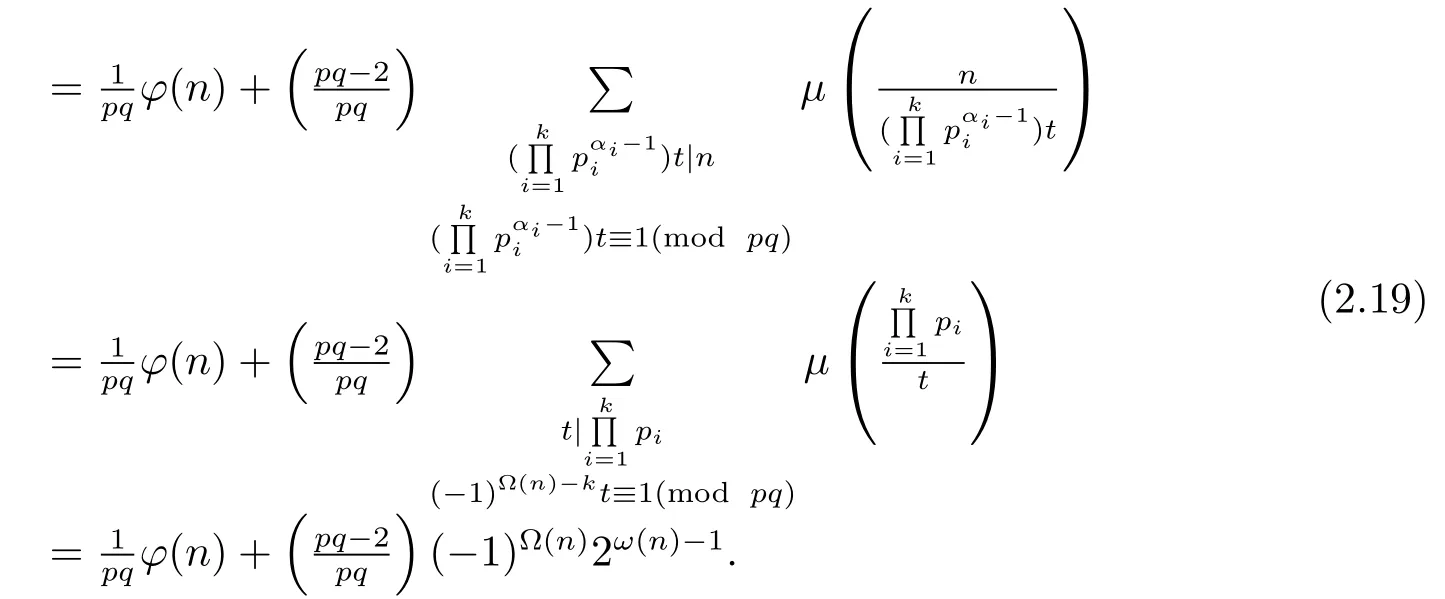
From(2.18)–(2.19),we complete the proof of(1).
(2) Forα=1 andβ=0,i.e.,n=pn1,then by gcd(pq,n1)=gcd(p,q)=1,we have
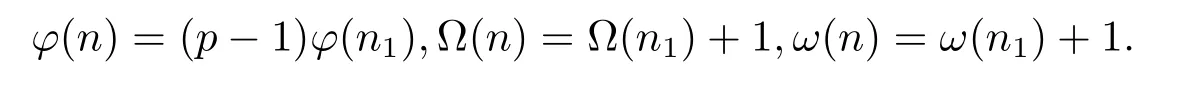
(i) Ifpi≡1(modpq),thenpi≡1(modq)(i=1,···,k).And so by Theorem 1.1,Theorem 1.4 and(2.18),we have
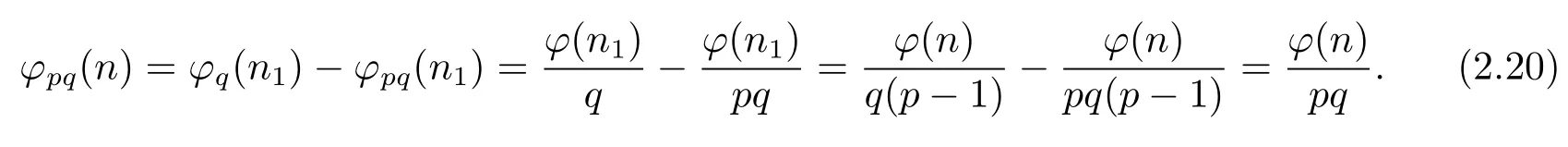
(ii) Ifpi≡?1(modpq),thenpi≡?1(modq)(i=1,···,k),thus by Theorem 1.1,Theorem 1.4,and(2.19),we have
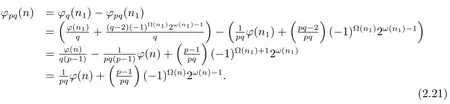
Now from(2.20)–(2.21),we complete the proof of(2).
(3) Forα=0 andβ=1,in the same proof as that of(2),the result is immediate.
(4) Forα=β=1,i.e.,n=pqn1,then by gcd(pq,n1)=gcd(p,q)=1,we have
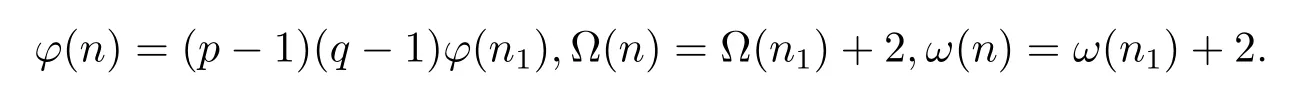
(i) Ifpi≡1(modpq),i.e.,pi≡1(modq)andpi≡1(modq)(i=1,···,k).Then by Theorem 1.1,Theorem 1.4 and(2.18),we have
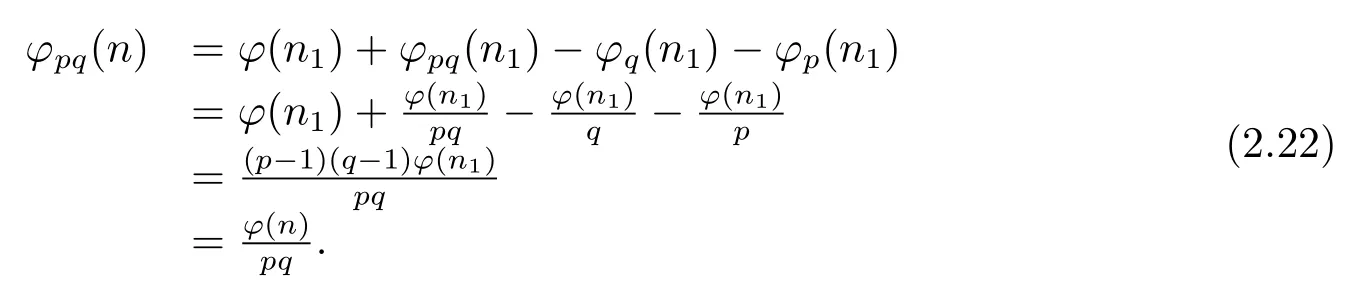
(ii) Ifpi≡?1(modpq),then by Theorem 1.1,Theorem 1.4 and(2.19),we have
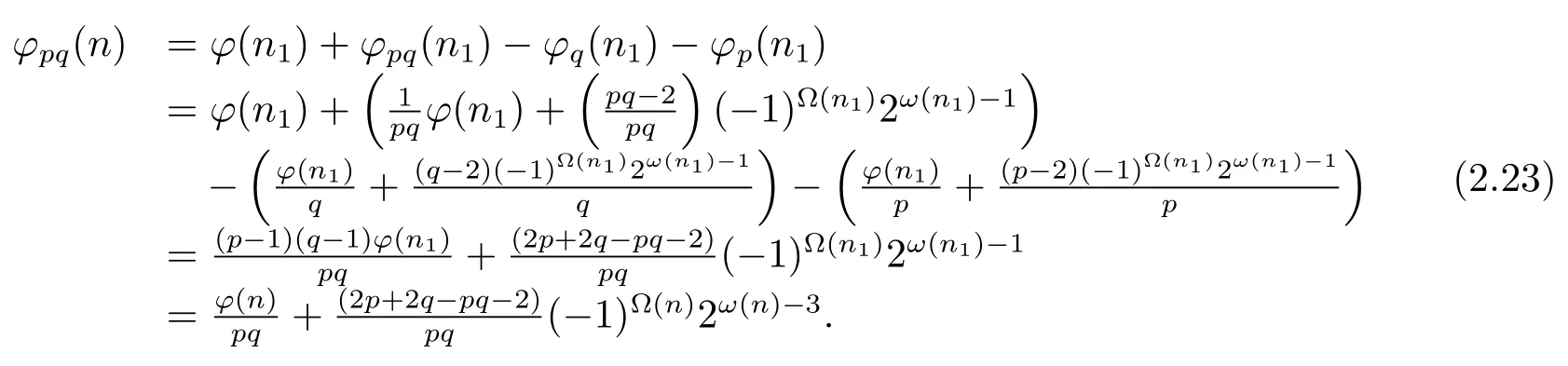
Now from(2.22)–(2.23),we complete the proof of(4).
(5) Forα≥2 andβ=0,i.e.,n=pαn1,then by gcd(n1,pq)=gcd(p,q)=1,we have
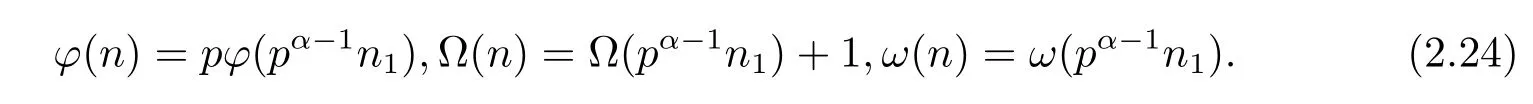
(i) Ifp≡pi≡1(modq)(i=1,···,k),then by Theorem 1.1,Theorem 1.4 and(2.24),we have
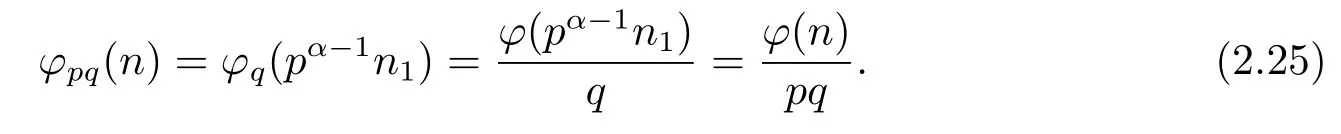
(ii) Ifp≡pi≡?1(modq)(i=1,···,k),then by Theorem 1.1,Theorem 1.4 and(2.24),we have
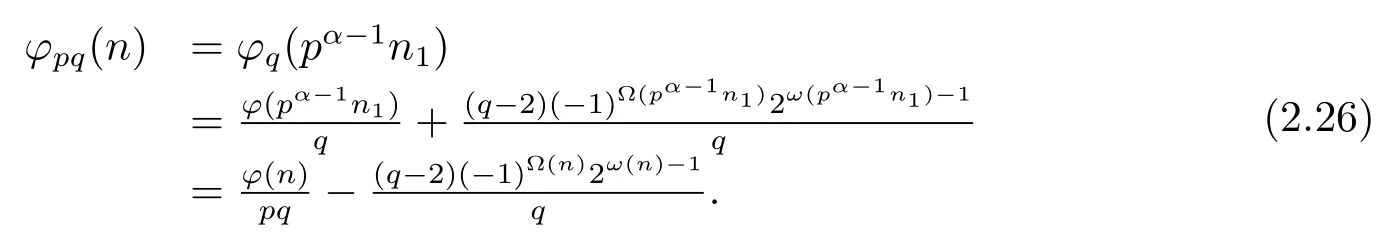
Now from(2.25)–(2.26),we complete the proof of(5).
(6) Forα≥2 andβ=1,i.e.,n=pαqn1,then by gcd(n1,pq)=gcd(p,q)=1,we have
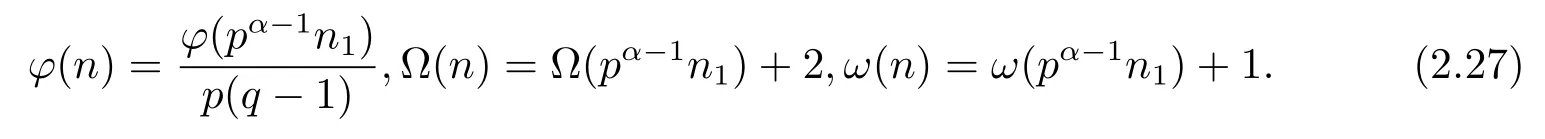
(i) Ifp≡pi≡1(modq)(i=1,···,k),then by Theorem 1.1,Theorem 1.4 and(2.27),we have
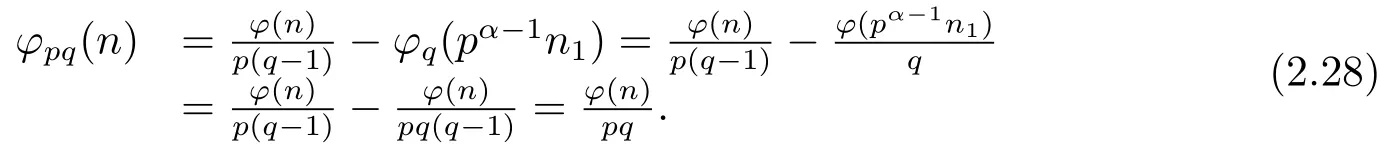
(ii) Ifp≡pi≡?1(modq)(i=1,···,k),then by Theorem 1.1,Theorem 1.4 and(2.27),in the same proof as that of case(5)(ii),one can get
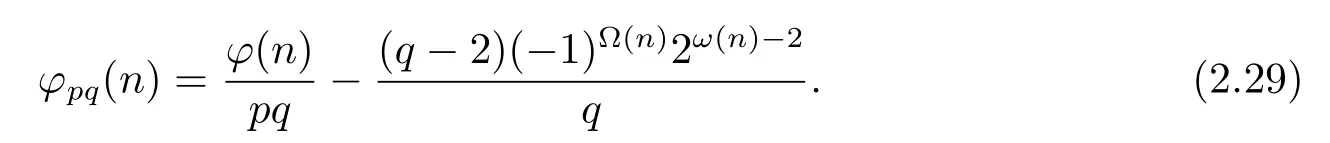
Now from(2.28)–(2.29),we complete the proof of(6).
(7) Ifβ≥2 andα=0 or 1,in the same proofs as those of(4)and(5),the result is obvious.
From the above,Theorem 1.5 is proved.
- 數學雜志的其它文章
- 最大度為6的圖G的鄰點可區別邊色數的一個上界
- EXISTENCE OF SOLUTIONS AND ERROR BOUNDS FOR A GENERALIZED INVERSE MIXED QUASI-VARIATATIONAL INEQUALITY
- CENTRAL LIMIT THEOREM AND MODERATE DEVIATION FOR NONHOMOGENENOUS MARKOV CHAINS
- SELF-ADAPTIVE SLIDING MODE SYNCHRONIZATION OF A CLASS OF UNCERTAIN FRACTIONAL-ORDER VICTOR-CARMEN SYSTEMS
- TO CONSTRUCT SOLUTIONS OF THE DIMENSIONALLY REDUCED VARIABLE-COEFFICIENT B-TYPE KADOMTSEV-PETVIASHVILI EQUATION
- FORCED OSCILLATION OF FRACTIONAL PARTIAL DIFFERENTIAL EQUATIONS WITH DAMPING TERM

