CENTRAL LIMIT THEOREM AND MODERATE DEVIATION FOR NONHOMOGENENOUS MARKOV CHAINS
XU Ming-zhou,DING Yun-zheng,ZHOU Yong-zheng
(School of Information and Engineering,Jingdezhen Ceramic Institute,Jingdezhen 333403,China)
Abstract:In this article,we study central limit theorem for countable nonhomogeneous Markov chain under the condition of uniform convergence of transition probability matrices for countable nonhomogeneous Markov chain in Ces`aro sense.By Grtner-Ellis theorem and exponential equivalent method,we obtain a corresponding moderate deviation theorem for countable nonhomogeneous Markov chain.
Keywords:central limit theorem;moderate deviation;nonhomogeneous Markov chain;martingle
1 Introduction
Huang et al.[1]proved central limit theorem for nonhomogeneous Markov chain withfinite state space.Gao[2]obtained moderate deviation principles for homogeneous Markov chain.De Acosta[3]studied moderate deviations lower bounds for homogeneous Markov chain.De Acosta and Chen[4]established moderate deviations upper bounds for homogeneous Markov chain.It is natural and important to study central limit theorem and moderate deviation for countable nonhomogeneous Markov chain.We wish to investigate a central limit theorem and moderate deviation for countable nonhomogeneous Markov chain under the condition of uniform convergence of transition probability matrices for countable nonhomogeneous Markov chain in Ces`aro sense.
Suppose that{Xn,n≥0}is a nonhomogeneous Markov chain taking values inS={1,2,···}with initial probability

and the transition matrices
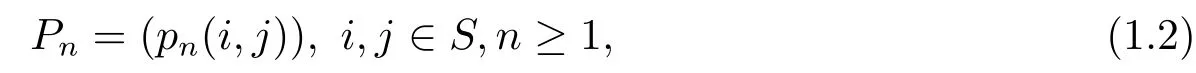
wherepn(i,j)=P(Xn=j|Xn?1=i).Write

When the Markov chain is homogeneous,P,Pkdenote,respectively.
IfPis a stochastic matrix,then we write
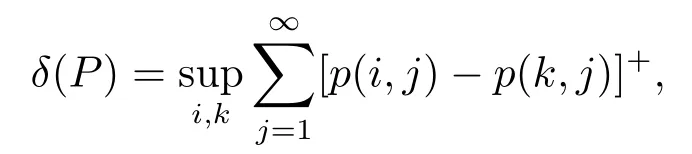
where[a]+=max{0,a}.
LetA=(aij)be a matrix defined asS×S.Write.
Ifh=(h1,h2,···),then we write.Ifg=(g1,g2,···)0,then we write|.The properties below hold(see Yang[5,6])
(a)kABk≤kAkkBkfor all matricesAandB;
(b)kPk=1 for all stochastic matrixP.
Suppose thatRis a‘constant’stochastic matrix each row of which is the same.Then{Pn,n≥1}is said to be strongly ergodic(with a constant stochastic matrixR)if for all.The sequence{Pn,n≥1}is said to converge in the Cesro sense(to a constant stochastic matrixR)if for everym≥0,
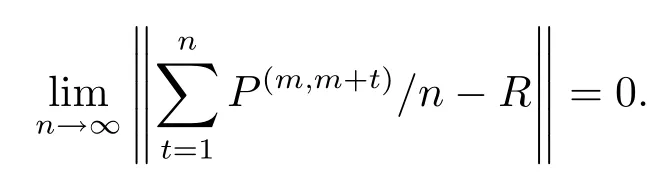
The sequence{Pn,n≥1}is said to uniformly converge in the Ces`aro sense(to a constant stochastic matrixR)if
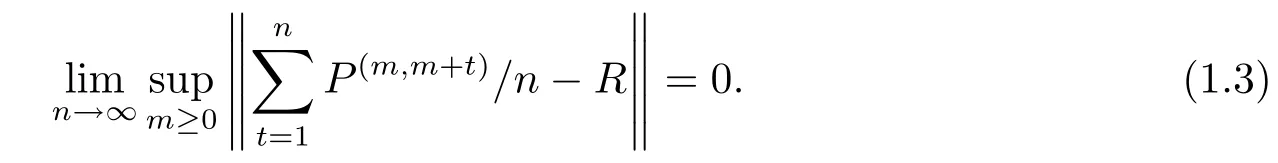
Sis divided intoddisjoint subspacesC0,C1,···,Cd?1,by an irreducible stochastic matrixP,of periodd(d≥1)(see Theorem 3.3 of Hu[7]),andPdgivesdstochastic matrices{Tl,0≤l≤d?1},whereTlis defined onCl.As in Bowerman et al.[8]and Yang[5],we shall discuss such an irreducible stochastic matrixP,of perioddthatTlis strongly ergodic forl=0,1,···,d?1.This matrix will be called periodic strongly ergodic.
Remark 1.1IfS={1,2,···},d=2,P=(p(i,j)),p(1,2)=1,p(k,k?1)=,thenPis an irreducible stochastic matrix of period 2.Moreover,
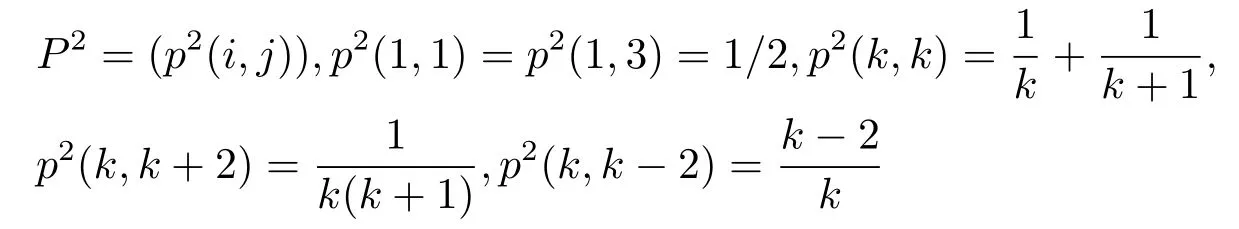
fork≥2.
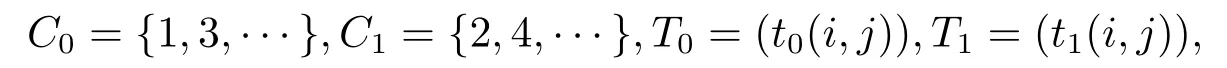
where
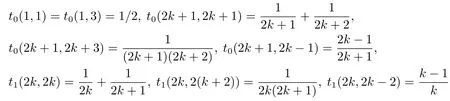
fork≥1.The solution ofπP=πandare
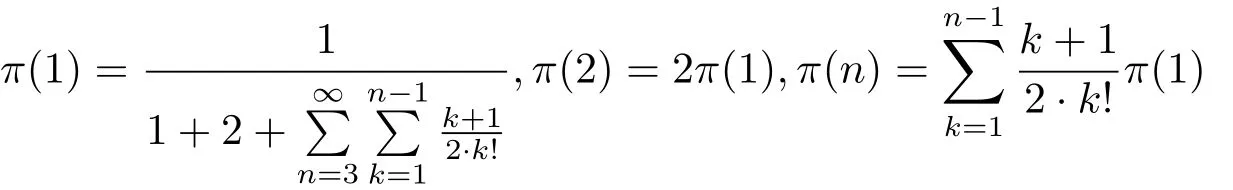
forn≥3.
Theorem 1.1Suppose{Xn,n≥0}is a countable nonhomogeneous Markov chain taking values inS={1,2,···}with initial distribution of(1.1)and transition matrices of(1.2).Assume thatfis a real function satisfying|f(x)|≤Mfor allx∈R.Suppose thatPis a periodic strongly ergodic stochastic matrix.Assume thatRis a constant stochastic matrix each row of which is the left eigenvectorπ=(π(1),π(2),···)ofPsatisfyingπP=πand.Assume that
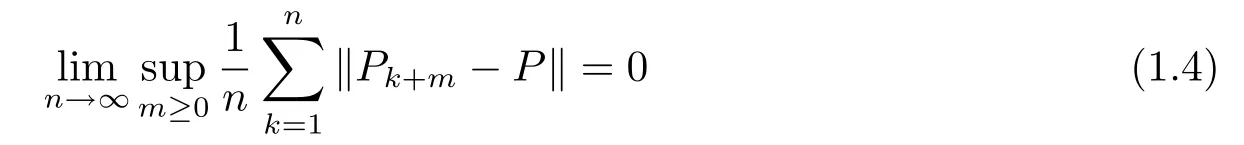
and
Moreover,if the sequence ofδ-coefficient satisfies

then we have

Theorem 1.2Under the hypotheses of Theorem 1.1,if moreover
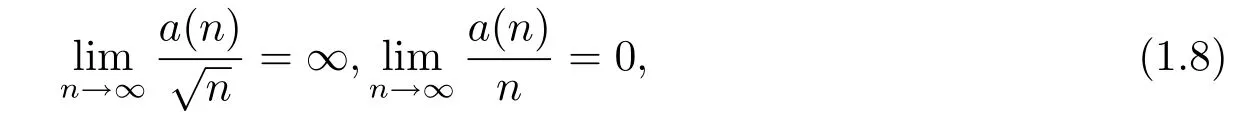
then for each open setG?R1,
and for each closed setF?R1,
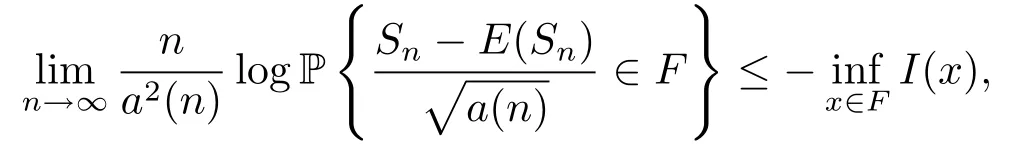
In Sections 2 and 3,we prove Theorems 1.1 and 1.2.The ideas of proofs of Theorem 1.1 come from Huang et al.[1]and Yang[5].
2 Proof of Theorem 1.1
Let
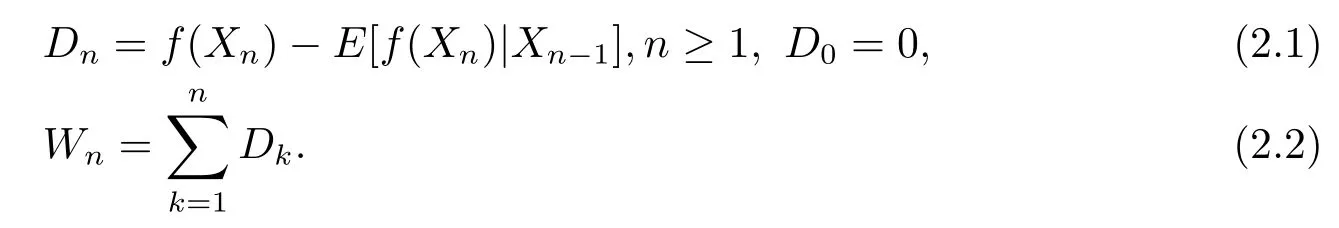
WriteFn=σ(Xk,0≤k≤n).Then{Wn,Fn,n≥1}is a martingale,so that{Dn,Fn,n≥0}is the related martingale difference.Forn=1,2,···,set
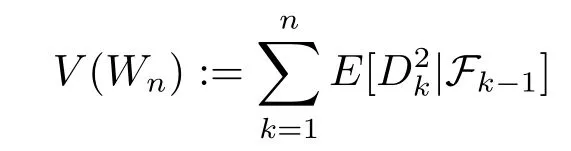
and
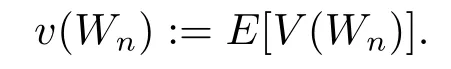
It is clear that
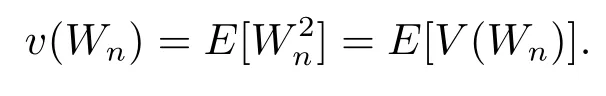
As in Huang et al.[1],to prove Theorem 1.1,we first state the central limit theorem associated with the stochastic sequence of{Wn}n≥1,which is a key step to establish Theorem 1.1.
Lemma 2.1Assume{Xn,n≥0}is a countable nonhomogeneous Markov chain taking values inS={1,2,···}with initial distribution of(1.1)and transition matrices of(1.2).Supposefis a real function satisfying|f(x)|≤Mfor allx∈R.Assume thatPis a periodic strongly ergodic stochastic matrix,andRis a constant stochastic matrix each row of which is the left eigenvectorπ=(π(1),π(2),···)ofPsatisfyingπP=πand.Suppose that(1.4)and(1.5)are satisfied,and{Wn,n≥0}is defined by(2.2).Then

As in Huang et al.[1],to establish Lemma 2.1,we need two important statements below such as Lemma 2.2(see Brown[9])and Lemma 2.3(see Yang[6]).
Lemma 2.2Assume that(?,F,P)is a probability space,and{Fn,n=1,2,···}is an increasing sequence ofσ-algebras.Suppose that{Mn,Fn,n=1,2,···}is a martingale,denote its related martingale difference byξ0=0,ξn=Mn?Mn?1(n=1,2,···).Forn=1,2,···,write
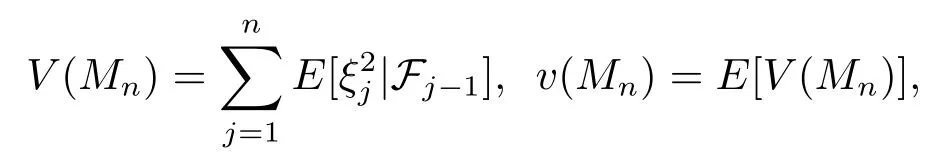
whereF0is the trivialσ-algebra.Assume that the following holds
(i)

(ii)the Lindeberg condition holds,i.e.,for any?>0,
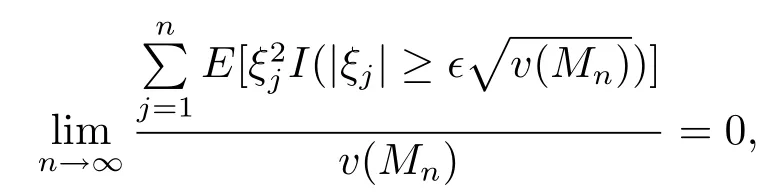
whereI(·)denotes the indicator function.Then we have

Writeδi(j)=δij,(i,j∈S).Set
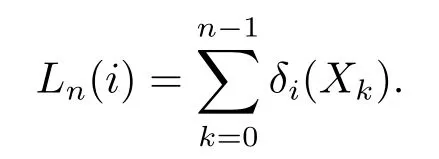
Lemma 2.3Assume that{Xn,n≥0}is a countable nonhomogeneous Markov chain taking values inS={1,2,···}with initial distribution(1.1),and transition matrices(1.2).Suppose thatPis a periodic strongly ergodic stochastic matrix,andRis matrix each row of which is the left eigenvectorπ=(π(1),π(2),···)ofPsatisfyingπP=πand.Assume(1.4)holds.Then

Now let’s come to establish Lemma 2.1.
Proof of Lemma 2.1Applications of properties of the conditional expectation and Markov chains yield
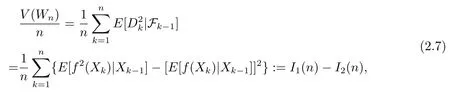
where
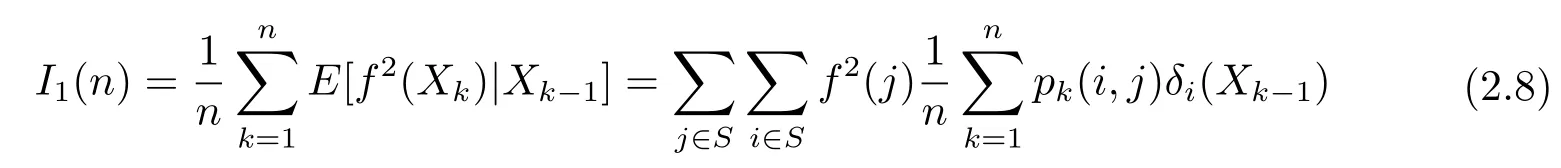
and
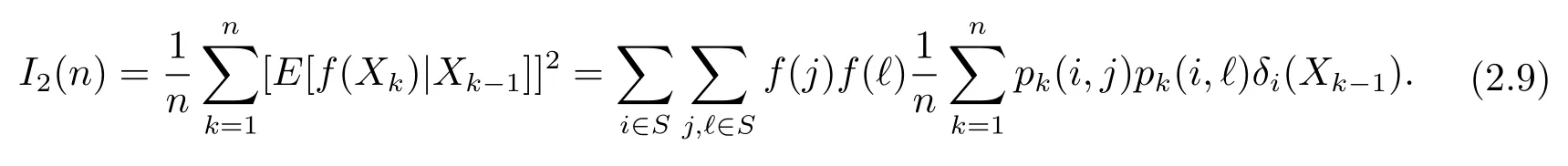
We first use(1.4)and Fubini’s theorem to obtain
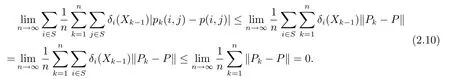
Hence,it follows from(2.10)andπP=πthat
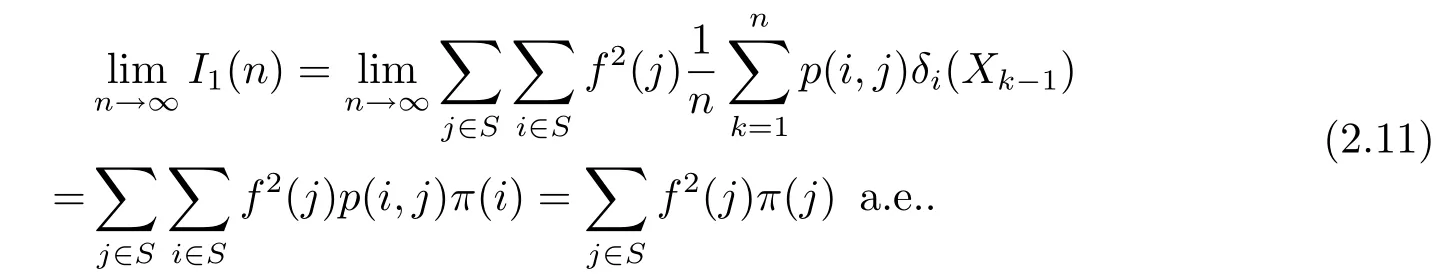
We next claim that
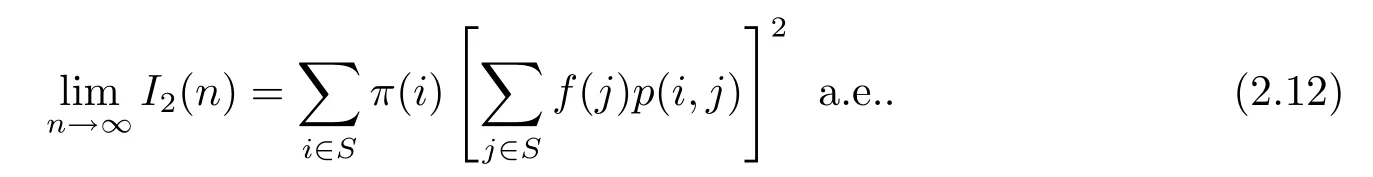
Indeed,we use(1.4)and(2.9)to have
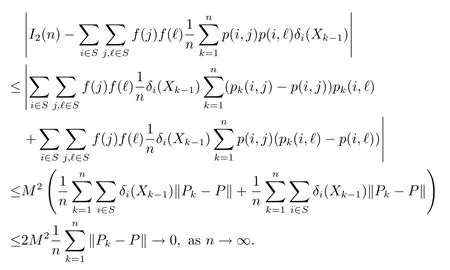
Thus we use Lemma 2.3 again to obtain
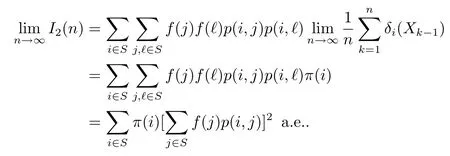
Therefore(2.12)holds.Combining(2.11)and(2.12)results in
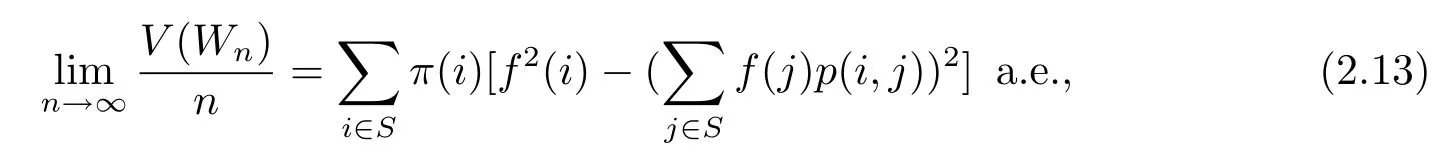
which gives
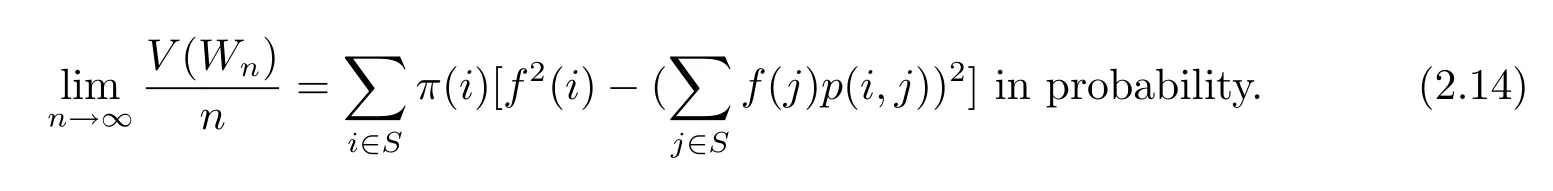
Since{V(Wn)/n,n≥1}is uniformly bounded,{V(Wn)/n,n≥1}is uniformly integrable.By applying the above two facts,and(1.5),we have

Therefore we obtain
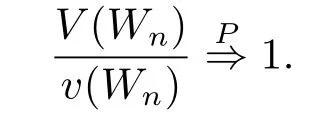
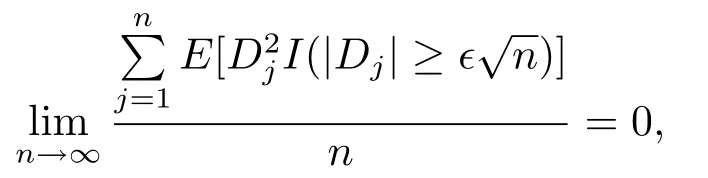
which implies that the Lindeberg condition holds.Application of Lemma 2.2 yields(2.3).This establishes Lemma 2.1.
Proof of Theorem 1.1Note that
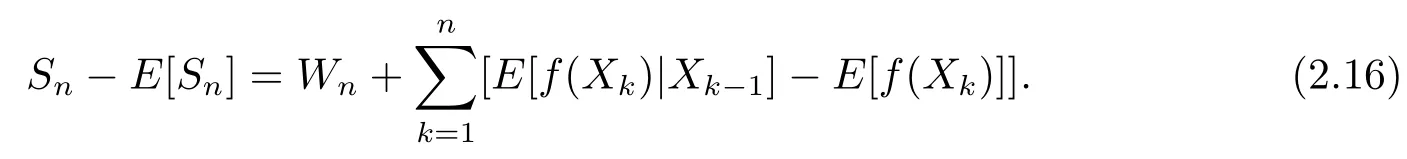
Write
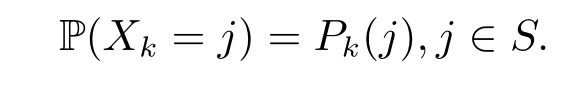
Let’s evaluate the upper bound of|E[f(Xk)|Xk?1]?E[f(Xk)]|.In fact,we use the C-K formula of Markov chain to obtain
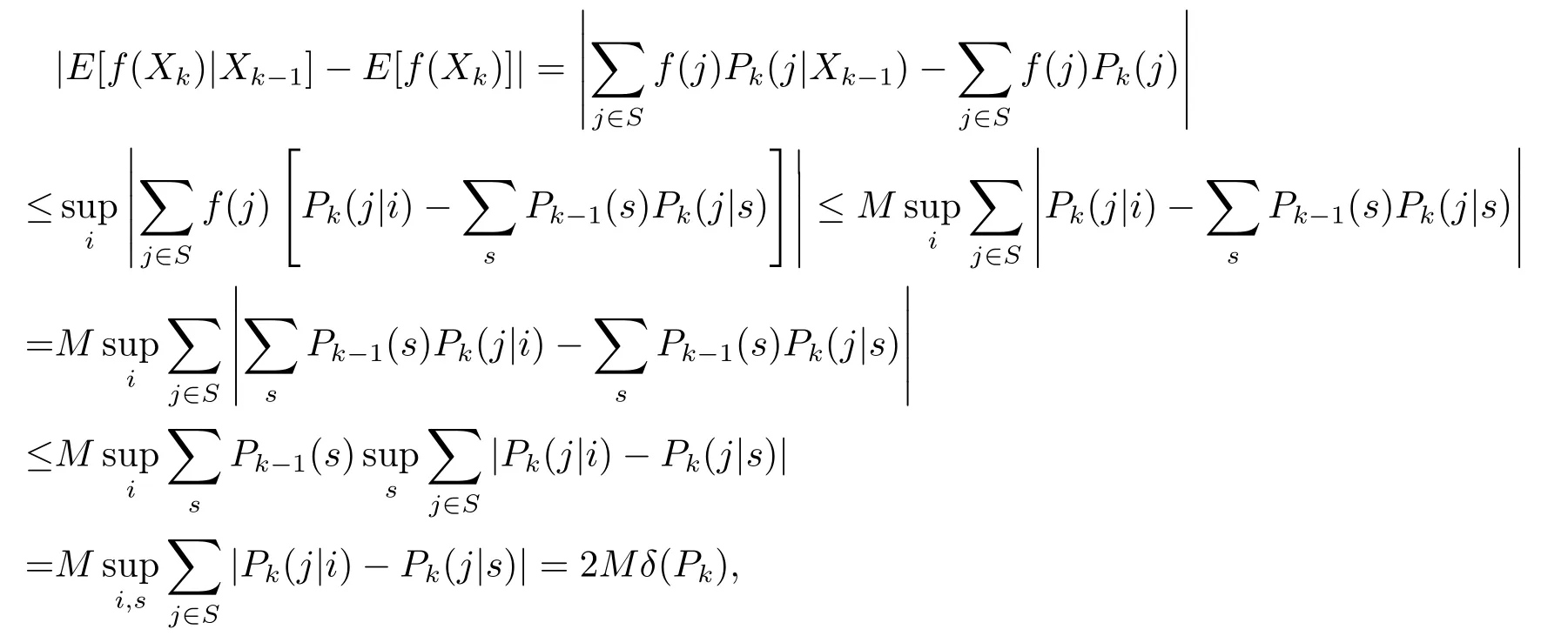
here
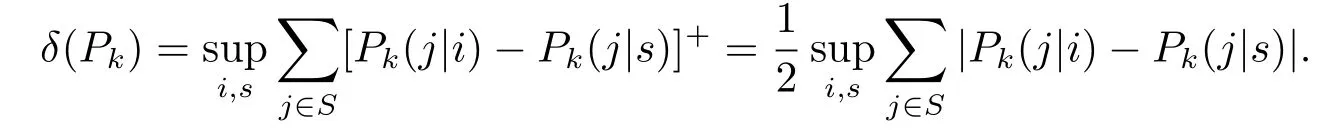
Application of(1.6)yields
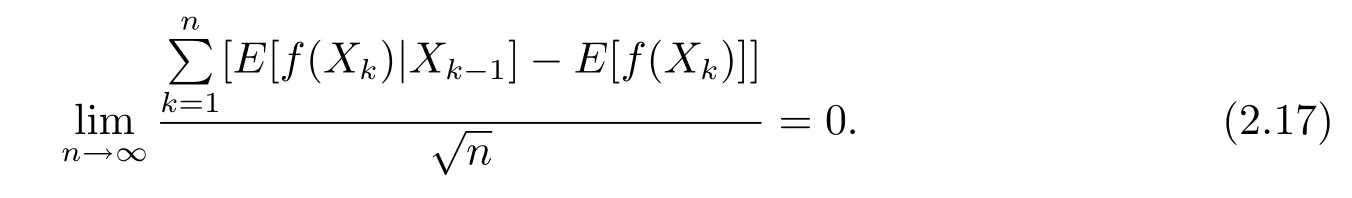
Combining(1.6),(2.3),(2.16),and(2.17),results in(1.7).This proves Theorem 1.1.
3 Proof of Theorem 1.2
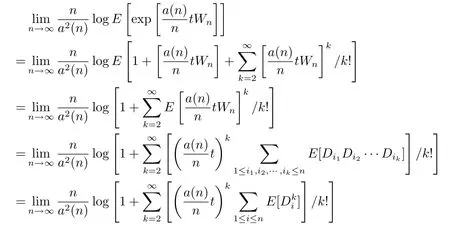
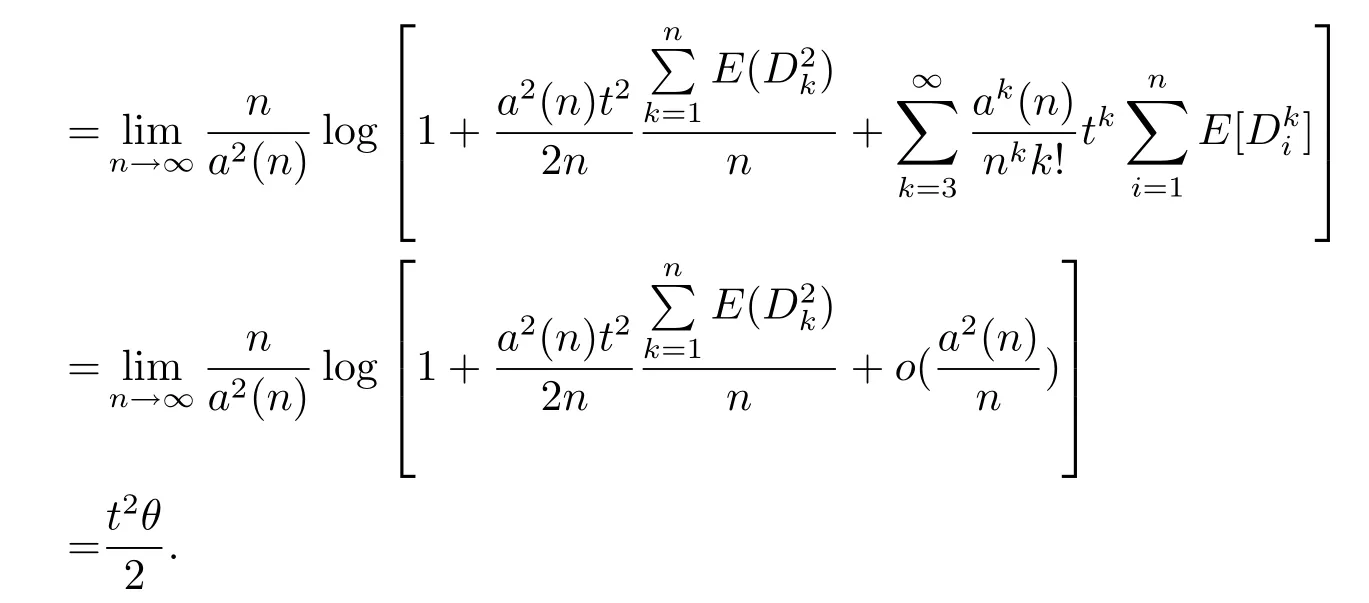
In fact,by(1.8),
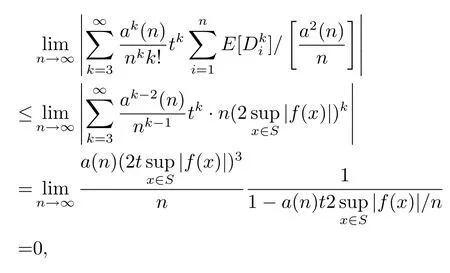
and the claim is proved.Hence,by using Grtner-Ellis theorem,we deduce thatWn/a(n)satisfies the moderate deviation theorem with rate function.It follows from(1.8)and(2.17)that??>0,
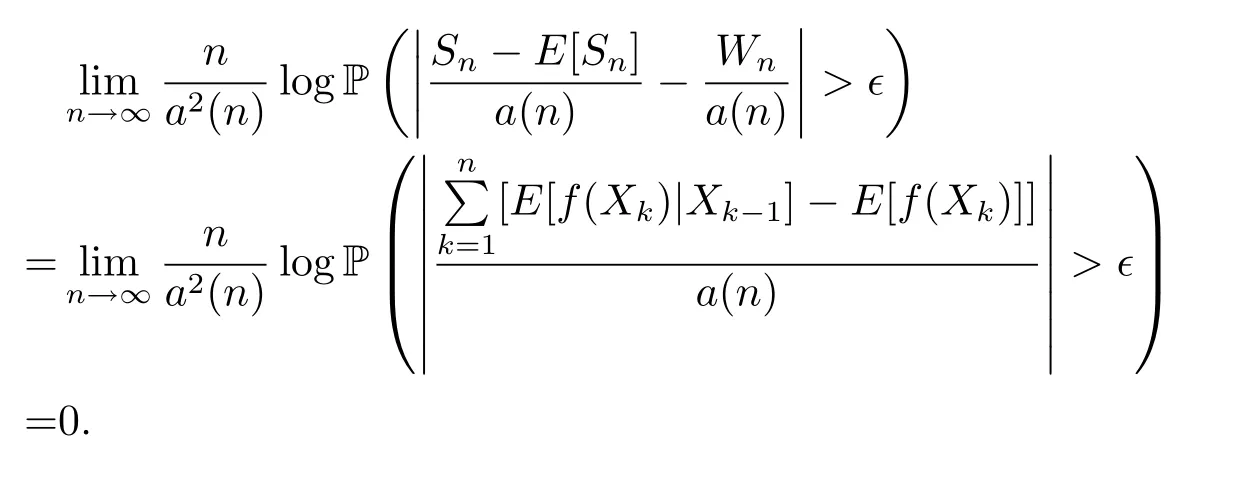
Thus,by the exponential equivalent method(see Theorem 4.2.13 of Dembo and Zeitouni[10],Gao[11]),we see thatsatisfies the same moderate deviation theorem aswith rate function.This completes the proof.
- 數學雜志的其它文章
- 最大度為6的圖G的鄰點可區別邊色數的一個上界
- EXISTENCE OF SOLUTIONS AND ERROR BOUNDS FOR A GENERALIZED INVERSE MIXED QUASI-VARIATATIONAL INEQUALITY
- SELF-ADAPTIVE SLIDING MODE SYNCHRONIZATION OF A CLASS OF UNCERTAIN FRACTIONAL-ORDER VICTOR-CARMEN SYSTEMS
- TO CONSTRUCT SOLUTIONS OF THE DIMENSIONALLY REDUCED VARIABLE-COEFFICIENT B-TYPE KADOMTSEV-PETVIASHVILI EQUATION
- FORCED OSCILLATION OF FRACTIONAL PARTIAL DIFFERENTIAL EQUATIONS WITH DAMPING TERM
- THE COMPUTING FORMULA FOR TWO CLASSES OF GENERALIZED EULER FUNCTIONS

