單軸壓縮下砂巖斷裂試驗及細觀統計損傷模型

李漢章，束加慶，王海軍，任旭華，湯 雷

(1.河海大學，江蘇 南京 210098；2.江蘇省電力設計院，江蘇 南京 211102；3.南京水利科學研究院，水文水資源與水利工程科學國家重點實驗室，江蘇 南京 210029)

在外荷載和環境作用下，材料的微缺陷如微裂紋、微孔洞等的出現和擴展而導致其宏觀力學性質逐步裂化的過程稱為損傷[1]。而損傷力學是專門研究含微裂紋或微孔洞介質材料損傷的演化發展直至破壞的學科，由Kachnov[2]和Rabotno[3]創立，現已被廣泛應用于各個工程領域，成為固體力學研究的一個前沿。

巖體是典型的非均勻性材料，內部含有微裂紋、顆粒接觸面等[4-6]缺陷。Dougill[7]在巖石和混凝土材料中開始使用損傷力學，隨后損傷模型及演變方程不斷涌現。Krajcinovic[8]將統計理論引入損傷力學用于描述巖石材料內部缺陷分布的隨機性，為巖石統計損傷理論提出全新的思路。國內唐春安等[9-10]和謝和平等[11]分別從巖石微元的強度和損傷耗散能釋放率服從某種隨機分布的角度出發，建立相應的損傷本構方程，又使巖石的損傷統計本構模型研究取得了重大進展。曹文貴等[12-15]在此基礎上，與室內試驗相結合引入巖石微元參數，進而提出了能夠反映巖石脆-延特性及其相互轉化的巖石損傷統計本構模型。建立三維巖石損傷破裂本構模型模擬巖石宏細觀力學特性，是損傷力學中的首要問題之一。

按傳統損傷理論模型，當單元完全損傷破壞時，將不具備任何承載能力，隨著荷載的作用下，損傷部位將發生無限的位移。這是數值實驗和物理實驗之間的一個差別，即在數值實驗中，兩個不相連的單元碰撞如若不考慮之間的接觸不會產生相互作用，而會發生互相嵌入。但是，真實情況下對于壓破壞的損傷部位雖然發生破壞，物質本身不可能消失，特別是在周邊物質的限制下，會出現損傷部位慢慢壓實，重新承受荷載的情況，類似于“愈合”。

為了模擬壓縮狀態下的這種“接觸愈合”作用，本文將給壓縮狀態下完全破壞了的細觀單元賦予一定的承壓能力，使其成為“接觸單元”。對該單元而言，即表現為損傷得到了一定程度上的“愈合”。首先開展單軸壓縮下砂巖破壞試驗，然后系統闡述了考慮峰后承載特性的細觀損傷本構模型，包括本構方程、損傷變量演化、材料非均勻性模擬方法；給出基于細觀損傷力學模型的數值模擬及物理實驗結果，并對應力～應變曲線、宏觀損傷斷裂特征進行了對比分析；最后給出結論。本文研究為進一步開展不同荷載條件及巖體工程分析應用奠定了基礎。

1 單軸壓縮試驗

1.1 試驗方案

采用砂巖材料，按照國際巖石力學學會建議標準制作為高徑比2∶1標準圓柱形試樣，密度2 940 kg/m3。加載試驗采用三思縱橫WAW-600微機控制電液伺服加載系統，包含最大試驗力600 kN的萬能試驗機，DSCC-5000多通道電液伺服閉環控制系統，位移測量范圍0～200 mm,可采用應力及位移兩種加載方式，本實驗采用應力加載控制方式，加載速率為7 MPa/min。每種加載方式采用不同的應力值控制。物理實驗中采用應變片測量，在圓柱形試樣的側面按照0°、180°黏貼。采用多通道數據采集系統,加載系統及數據采集系統見圖1。

1.2 試驗結果

單軸壓縮下砂巖試樣典型應力～應變曲線見圖2，彈性模量為26.6 GPa，單軸抗壓強度為38.5 MPa，呈現脆性破壞。試樣破壞形態見圖3,巖石力學參數整理見表1。

表1 巖石力學參數

2 細觀損傷模型

2.1 細觀損傷本構方程

本文所建立的損傷本構方程及損傷演化特性，充分考慮了壓縮荷載作用下，破壞單元將轉化為能繼續承受壓力荷載的“接觸單元”，因此，本文建立的巖石細觀損傷本構模型能夠模擬出巖石試樣損傷部位的愈合特征。因而試樣在峰值應力后的殘余強度得到體現。

由Lemaitre應變等價原理[15]，即受損材料在應力作用下的應變與無損材料在有效應力下的應變可以等價，建立起細觀單元的損傷本構方程。

σ=Eε=σ(1-D)=E0(1-D)ε

(1)

式中E0——損傷前細觀單元的彈性模量；E——損傷后細觀單元的彈性模量；D——細觀單元的損傷變量值。

圖4為細觀單元在單軸荷載作用下的應力應變曲線。細觀單元在單軸壓縮荷載作用下，在壓縮應力沒有達到單元壓縮強度之前，單元為完全彈性體，計算參數由彈性模量和泊松比確定；隨著應力達到峰值應力σc時，單元發生脆性壓縮損傷，在應力～應變曲線圖上表現為應力的突然降低，此時單元的力學參數發生折減，并認為發生損傷后巖石仍能承受較小荷載；在壓縮應變達到某一極值εcu時，認為此時損傷物質被完全壓碎，單元主壓應力兩側相鄰單元發生接觸。單元在單軸拉伸荷載作用下，當拉伸應力達到單元拉伸強度前，單元為完全線彈性體；當應力超過單元拉伸強度時，發生脆性拉伸損傷；當拉伸應變達到某一極值εtu時，認為單元被完全拉壞，不具備任何承載能力。

2.2 損傷變量演化

見圖4，細觀單元中單軸受拉壓狀態下的一維損傷變量演化規律，在單軸拉伸應力狀態下，損傷變量的表達式為：

(2)

在單軸壓縮應力狀態下，損傷變量的表達式為：

公路橋梁養護作為一項兼具科學性與嚴謹性的工作，要求其工作人員具備較高的職業素養。首先，有關部門在公路橋梁工作人員的招聘方面要將更多的關注點放在工作人員的道路養護技術水平與職業素養的提升方面，在對員工進行招聘后還要定期對公路橋梁養護的工作人員進行道路養護標準化流程的相關知識培訓，不斷提高工作人員的職業素養與技術水平；其次，有關企業還要定期對員工進行職業素養的培訓，通過宣傳力度的加強來使員工意識到公路橋梁養護的重要性，以此為基礎增強自身工作的責任感與使命感，進而深度挖掘員工公路橋梁養護的工作潛力[6]。

(3)

式中E0——單元初始彈模；σc——無側限抗壓強度；εcu——σc下峰值壓應變；σcr——殘余壓強；λ——單元的殘余強度系數，σcr=λcσc,σtr=λtσt;σt——細觀單元的單軸抗拉強度；σtr——單元初始拉伸破壞時的殘余強度；εt——彈性極限下峰值應變，定義為拉伸破壞應變閥值；εtu——極限拉伸應變,定義η為極限應變系數，εcu=ηεc。

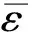
(4)

式中，ε1、ε2、ε3分別為主應變，〈〉是一個函數，意義如下：

(5)

當單元處于復雜應力狀態并滿足摩爾-庫倫準則時，可以得到單元的最大壓縮主應變εc0為：

(6)

在三維壓縮狀態下，用最大壓縮主應變ε3來代替式(3)中的單軸壓應變ε。如此，就可以將一維狀態下的損傷演化方程推廣到三維狀態下。

巖石細觀單元采用彈脆性損傷本構方程，選取具有拉伸截斷的摩爾-庫侖準則作為細觀單元破壞的準則。采用拉伸準則優先的原則，若單元受到的最大主應力達到單元拉伸強度時，細觀單元發生拉伸損傷，此時根據公式(2)確定損傷變量的大小，不以摩爾-庫侖作為判斷準則，在單元不滿足拉伸準則時，采用摩爾-庫侖準則作為判斷準則。

2.3 細觀非均勻性模擬

巖體是典型的非均勻性材料，其中含有裂紋、裂隙、成巖過程中的氣泡等缺陷。巖石顆粒從理論上講也應該是非均勻的，這種不均勻性可以用其力學參數的分布特性來描述。一般采用二參數Weibull分布用于描述巖石顆粒的細觀單元力學特性[17-18]：即形狀和尺度參數。形狀參數較之尺寸參數作用更大，控制分布密度曲線基本特征，尺度參數對于密度曲線形狀起到調節作用，另外可用于表示不同階段的失效情況。一般用W(μ0,m)表示二參數的Weibull分布，可由下式表示：

(7)

(8)

式中μ——分布參數的數值；m——形狀參數；μ0——尺度參數，是一個與所有單元參數平均值有關的參數，但并不是該參數的平均值，所以為了表述方便，文中稱之為均值。在模擬材料的非均勻性時也需要首先確定材料的m和μ0值，這兩個參數對Weibull分布的影響見圖5。

見圖5，參數m決定了分布的離散度，m越高，材料細觀單元力學參數越集中，m越小，材料參數越均勻，所有參數更接近于給定參數μ0。常數m數值模型中材料的細觀均勻性，可稱之為均值度。m越小，材料越均勻。對Weibull概率密度函數積分，得分布函數：

(9)

首先采用公式(9)生成數量與數值網格數量N相同個數的符合Weibull分布隨機數。將生成的隨機參數隨機賦予細觀單元。因此，這些單元體材料參數雖然具備離散型，但是整體符合統計分布規律，由此巖石類介質參數的隨機非均勻分布特性得到體現。

3 數值模擬及試驗結果分析

3.1 應力～應變曲線

巖石細觀參數通過遺傳算法進行反演分析得到。通過Fortran編寫遺傳算法程序及其與Abaqus接口程序，以宏觀參數彈性模量、試樣強度為反演目標，以形狀參數m、細觀單元強度均值FC、彈性模量E為反演參數。目標函數為彈模、強度與試驗中彈模、強度的誤差平方和。通過不斷試算反演參數值，使得目標函數值達到最小，由此確定最優反演參數。最終得到最佳細觀參數形狀參數m=7，細觀單元強度均值為FC=80 MPa，彈性模量均值為E=33 GPa。數值模擬中宏觀參數及物理實驗數據值見表2，十分接近。數值試驗與物理試驗的應力～應變曲線見圖6。

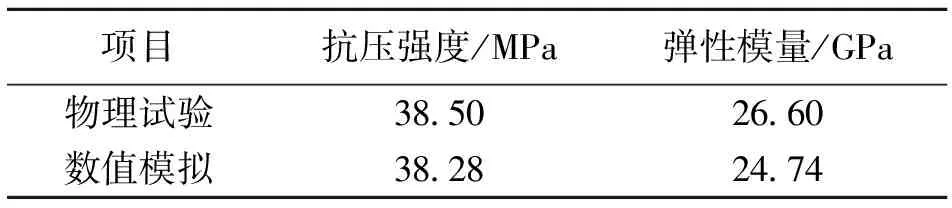
表2 巖石力學參數

3.2 應力分析

采用位移加載模式模擬單軸壓縮試驗。最小主應力隨加載步的分布演化規律見圖7，最大主應力隨加載步的分布演化規律見圖8。在荷載step6之前，位移加載較小，應力分布均勻。隨著壓縮位移的增大，壓應力逐漸增大，與均勻參數分布不同，出現應力分布不均的現象，如step16。由于巖石細觀參數的隨機分布，參數強弱不均，在參數相對軟弱的細觀單元處出現明顯的較大變形如step20，并在這些細觀單元處出現應力集中現象。

3.3 破壞形態分析

數值模擬計算不同位移加載步下的試樣損傷破壞過程見圖9。加載前期，由于細觀單元參數存在強弱差異，在參數相對較弱的單元，開始出現損傷，且為隨機分布，如step16。在step20時，損傷開始在左下角出現集聚。step22—24斷裂擴展面開始形成，并最終形成斷裂。設定狀態變量SDV1代表損傷值的大小，顏色越深表示損傷值越大。

數值模擬與實驗試樣最終破壞形態見圖10，在試樣下部發生剪切貫穿破壞。

4 結論

a) 建立了考慮細觀單元殘余強度的本構模型，并且實現了三維模型的單軸壓縮計算。模擬了材料逐漸從細觀損傷累積到集聚成核斷裂擴展直至破壞的過程。

b) 基于考慮細觀單元殘余強度的本構模型，通過Weibull分布模擬巖石細觀層次上力學參數的隨機性及宏觀統計分布規律，巖石宏觀破壞過程的復雜現象可以得到充分模擬。

c) 通過室內單軸壓縮實驗，得到了砂巖試樣的彈性模量、單軸抗壓強度、應力應變曲線及斷裂形態。砂巖宏觀參數與基于考慮細觀單元殘余強度的本構模型所得模擬結果一致，斷裂形態及破壞特征一致。本文本構模型的有效性得到驗證。