基于有限元法對異步電機電磁力的計算

(佳木斯電機股份有限公司，黑龍江佳木斯 154002)

0 引言

三相異步電動機的定子繞組中通入三相對稱的正弦電流后，經過定轉子之間的氣隙來產生旋轉磁場，轉子導體將切割磁力線而產生感應電動勢。但在實際電機中，由于磁極磁場并非完全按正弦規律分布，因此，定子繞組內的感應電動勢也不完全是正弦波形，即除了正弦波形的基波外還包含著一系列的諧波。因此在氣隙磁勢中，除了基波產生的旋轉主磁場外，還有一系列由諧波產生的諧波磁場。基波主磁場和諧波磁場所感應產生的轉子電流在氣隙中所產生的磁勢都可分解成一系列不同次數的磁勢，從而構成了齒諧波。齒諧波的存在，使電機損耗增大，電磁力增加，加劇了電機電磁噪聲的產生。因此，研究電磁力大小對研究電磁噪聲有重要意義。

電磁力經典的計算方法是采用解析法，但其數據較多，計算過程復雜。隨著目前仿真軟件的蓬勃發展，利用有限元法計算電磁力更為方便快捷。通過有限差分或有限元法求出氣隙磁位，再利用經典虛位移法或者麥克斯韋張量法求出電磁力。求得的值不僅包括徑向分量，連切向力也可計算在內，計算精度高，計算方案多，可以計及飽和作用。

1 電磁力的有限元法計算過程

有限元法又稱有限單元法，是從變分原理、加權余量法出發，結合模型的剖分單元和所選擇的插值函數來建立及求解數理方程的一種離散化得解法。

電磁場的有限元分析過程大致如下。

(1)建立問題的變分表述，從待解的磁場邊值問題出發，利用變分原理把求解問題轉化為能量泛函的極值問題。

(2)將模型剖分，將求解區域劃分成若干單元，剖分單元分為三角形和多邊形，其節點可以是頂點也可以設為線段中點。

(3)選擇插值函數，即將變分問題變為求解數值解問題，用插值函數去逼近磁位函數或其它量值。

(4)將上述插值函數離散化，得到以n個節點為未知數的n階代數方程組，利用邊界條件求解代數方程組。

在電磁場計算中，通過有限元法得到的結果往往是節點的電勢或磁勢值，因此需要應用所求的電勢或磁勢值，并結合模型和劃分單元推導出如電磁力、電磁場儲能、電磁場強度等結論。

2 基于有限元法對異步電動機電磁力的計算

采用有限元法可以充分考慮電機鐵心結構的變化、氣隙磁場的高次諧波、磁路飽和等因素，通過一臺1200 kW-8異步電動機為例，建立電機的二維有限元模型，如圖1所示。

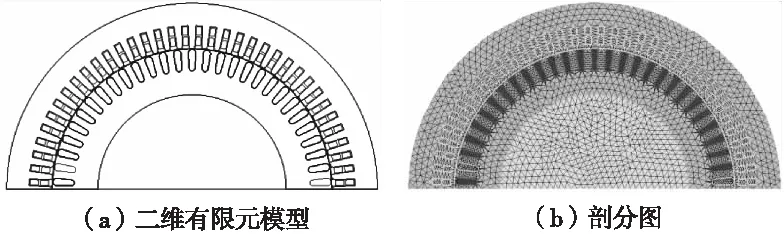
圖1 電機二維有限元模型及剖分圖

對磁場進行有限元分析的基本假設如下。

(1)磁場沿電機軸向不變，把問題作為二維磁場來處理。

(2)忽略定子繞組中渦流引起的集膚效應，認為電密在定子繞組截面上保持均勻。

(3)忽略溫度對電導率的影響，假定計算溫度為75℃。

(4)忽略電網中的諧波含量，認為激勵為正弦函數。

在所給定的求解區域內，用向量磁位A對數學模型進行表述。根據假設，A只有Z分量，則滿足的二維非線性恒定磁場的邊值問題為

(1)

式中,Js—電流密度的軸向分量；μ—磁導率。

電機穩定運行時的磁力線分布如圖2所示。

圖2 磁力線分布圖

該電機一對極下的氣隙磁密及其傅里葉分解結果見圖3。

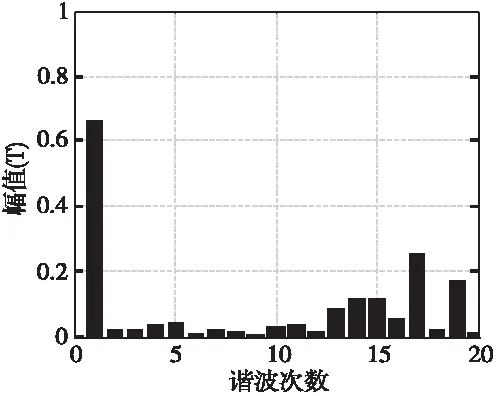
圖3 氣隙磁密諧波分析

為了分析方便，常將電磁力分為徑向分量和周向分量。周向電磁力形成電磁轉矩，是電動機轉動所需要的。徑向電磁力是不可避免的，它會引起定子振動而產生電磁噪聲，以下重點探討徑向電磁力。基于Maxwell應力張量理論，用等效磁張力(面積力)代替體積力可求出單位面積上的電磁力，它的徑向分量為

(2)

根據后處理得到氣隙磁密的徑向分量和切向分量，代入到上式得到該電機徑向電磁力隨時間的變化曲線，如圖4所示，其一個周期波形如圖5所示。

圖4 徑向電磁力隨時間變化曲線.

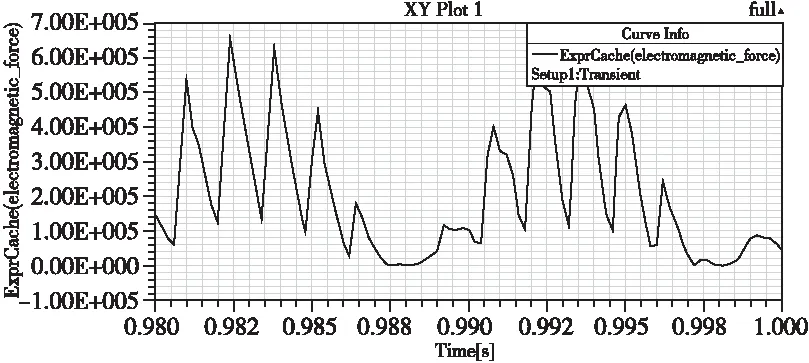
圖5 徑向電磁力一個周期曲線

將圖5波形進行快速傅里葉分解，得到結果如圖6所示。高頻段的放大圖如圖7所示。

圖6 徑向力的傅里葉分解

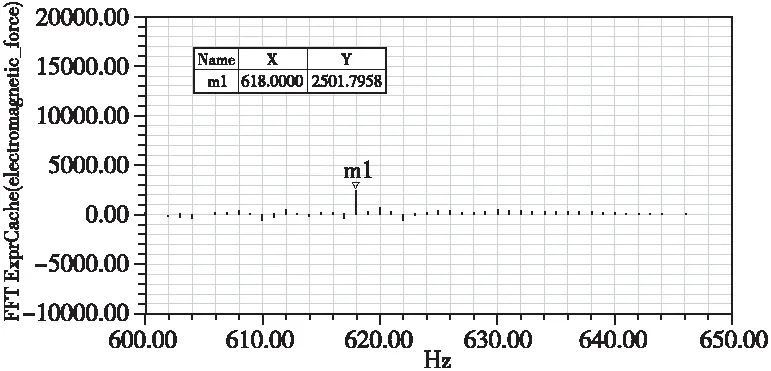
圖7 高頻段的放大圖

從圖6和圖7可以看出，由主播磁場引起的100Hz電磁力大小為80016.81Pa，由諧波磁場引起的較大的電磁力頻率為618Hz，大小為2501.79Pa。

3 結語

有限元分析法是求解各種復雜數學、物理問題的重要方法，是處理各種復雜工程問題的重要分析手段，也是進行科學研究的重要工具。本文采用有限元分析法對引起異步電動機電磁噪聲的電磁力進行仿真計算，以一臺異步電動機為例，建立有限元模型，并采用傅里葉分解對各次諧波電磁力大小進行計算。相對于解析法，有限元法方便快捷，具有一定的工程指導價值。