空爆沖擊波對高速破片繞流效應的仿真

鄭紅偉，陳長海，李 茂，朱 錫，侯海量

(海軍工程大學 艦船工程系，湖北 武漢 430033)

0 引 言

隨現代武器的迅速發展，對艦導彈成為當今武器研究的熱點之一。導彈爆炸產生的沖擊波和大量高速破片是聯合作用在結構上的2種最主要的毀傷元素[1]。戰斗部殼體的材料屬性、厚度、裝藥量、裝藥類型、殼體形狀和起爆方式都對沖擊波和高速破片的形成存在一定的影響[2-5]。早期，國內外學者關于沖擊波和高速破片的研究思路大多還是將2種載荷的解耦處理[6-7]，根據沖擊波和高速破片在空氣中的衰減特性，求解了沖擊波在前、相遇以及沖擊波在后的3個階段傳播規律[8]并將二者對結構的毀傷效應解耦成沖擊波沖量效應和高速破片穿甲作用2個問題分別研究[9]。但實際在整個傳播過程中2種載荷存在著相互影響。在載荷形成階段，破片的存在會使爆炸產生的一部分能量損耗于高速破片的形成，從而使沖擊波的能量減弱[10]。傳播階段，李茂等[11]在研究中指出沖擊波遇到破片時存在明顯的反射和繞流現象。沖擊波傳播過程中發生的繞流和反射現象會改變沖擊波的超壓、比沖量等載荷特性[12-13]，從而改變實際作用于結構的沖擊波強度。

為分析戰斗部空中爆炸后沖擊波對高速破片的繞流效應，可以更加真實地反映在傳播過程中沖擊波和高速破片的載荷特性。本文將采用Ansys/LS-DYNA非線性動力有限元分析軟件，對端部預制破片工況進行數值模擬。建立多個計算模型對比分析、破片尺寸和破片質量因素對沖擊波繞流作用的影響。

1 模型建立與仿真方法驗證

1.1 模型選擇及參數設置

數值模擬采用g-cm-μs單位制，模型由空氣域，破片，炸藥，鋼板4個部分組成。炸藥和空氣域均采用Euler單元，使用多物質單元ALE算法，預制破片和鋼板采用Lagrange單元。空氣域的尺寸取500 mm×500 mm×325 mm，模型布置和模型尺寸剖面示意圖如圖1所示。通過關鍵字*CONSTRAINED_LAGRANGE_IN_SOLID定義破片與空氣材料間的耦合算法。保證計算精度，模型網格密度應盡可能高，炸藥尺寸與炸藥網格尺寸比值至少應大于6[14-15]，但在有限元分析中單元劃分越細，節點數目越多，計算步長越短，計算時間越長。為減少計算時間，在保證主要研究區域的網格精度的前提下，空氣和鋼板模型均采用發散性網格。中心邊長140 mm的方形細化區域內，六面體網格邊長約為1 mm。最終劃分得到空氣域單元總數約50萬個，炸藥單元總數約7萬個，鋼板單元總數5.6萬個。通過試算，確定計算步長因子取0.65。仿真中歐拉域各面均設置無響應邊界條件，含鋼板模擬工況中鋼板四邊固支。

炸藥采用*MAT_HIGH_EXPLOSIVE_BURN本構模型，對轟爆產物的膨脹采用*EOS_JWL狀態方程來描述：

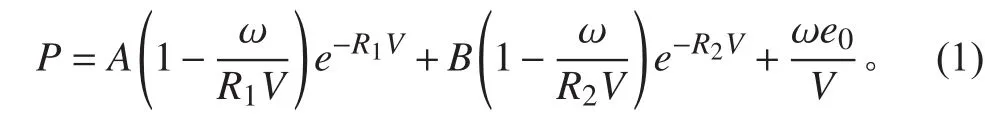
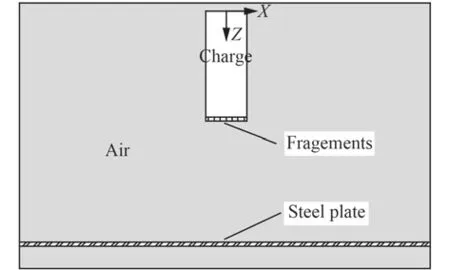
圖1 模型示意圖Fig. 1 Schematic diagram of the model

式中：P為轟爆壓力；e0為初始單位體積炸藥內能；V為相對體積。A，B，R1，R2，ω為試驗確定的常數，受裝藥密度、炸藥類型等因素的影響。具體參數如表1所示[17]。其中ρ為裝藥密度；D為爆轟速度；Pcj為壓力PCJ；V0為初始相對體積。每個炸藥單元的點火時間由該單元距離起爆點的距離和爆速決定。

表1 TNT炸藥材料參數及狀態方程參數Tab. 1 The materials and EOS parameters of TNT

空氣采用*MAT_NULL材料模型及*EOS_LINEAR_POLYNOMIAL狀態方程描述。狀態方程的線性多項式為：

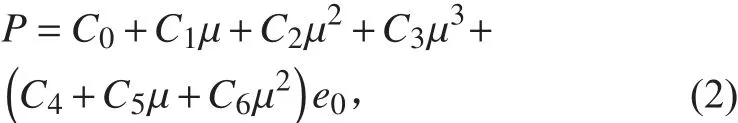
式中：C0～C6為多項式系數；e0為單位體積內能；μ=1/V-1，其中V為相對體積。當線性多項式狀態方程用于理想氣體模型時，空氣材料參數和狀態方程參數如表2所示。

表2 空氣材料參數及狀態方程參數Tab. 2 The materials and EOS parameters of air

破片采用雙線性彈塑性本構模型*MAT_PLASTIC_KINEMATIC，其應變率則由Cowper-Symonds模型描述，應變方程為：

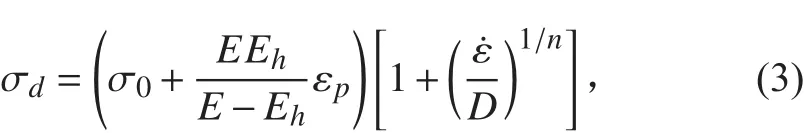
式中：σd為動態屈服強度；σ0為靜態屈服強度；E為彈性模量；Eh為硬化模量；εp為有效塑性應變；ε為等效塑性應變率；D，n為常數，對于常見低碳鋼，通常取 D=40.4 s-1，n=5[16]。

鋼板采用Johnson-Cook本構模型，該模型考慮了材料在高溫高應變率下的軟化效應，能夠反映高應變率以及高溫情況下材料的性質變化，其狀態方程為：

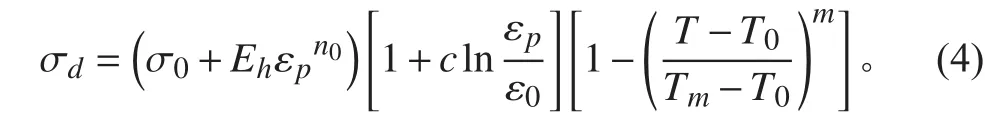
式中：n0為應變硬化指數；c為應變率系數；m為軟化指數；ε0為參考塑性應變率；T，Tm，T0分別為材料溫度，材料熔點和參考室溫，取Tm=1 793 K，T0=300 K。

材料的失效則由下述方程描述：

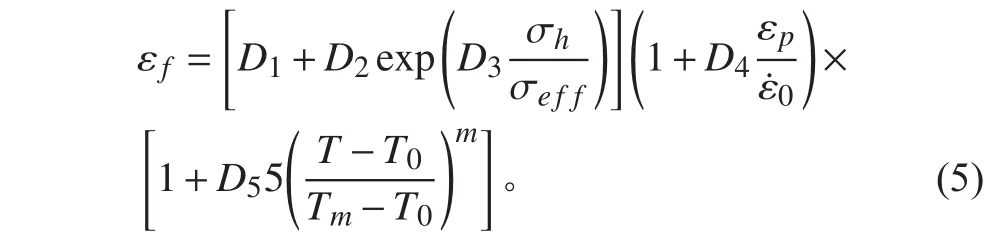
式中：D1～D5為材料無量綱常數；當破壞參數D =時，材料單元則判定為失效；σh為材料在三向應力下的靜水壓力；σeff為Mises等效應力。模型中鋼板和破片均采用Q235鋼，其力學參數及狀態方程參數如表3所示。

表3 Q235鋼力學參數及方程參數Tab. 3 The materials and EOS parameters of Q235

1.2 仿真方法驗證

為驗證模型建立的合理性，本文首先對空中近爆沖擊波載荷作用下鋼板的變形試驗[17]（模型1），近爆載荷聯合作用下鋼板變形毀傷試驗[18]（模型2）以及同樣裝藥工況下的2 mm和4 mm的Gurney平板驅動理論模型（模型3、模型4）進行仿真分析。模型中炸藥均為兩發直徑50 mm，高度65 mm的柱形鑄裝TNT軸向疊加布置，總裝藥質量400 g。炸藥下端面距離平板結構爆距為150 mm，模型1中鋼板厚度為4 mm，模型2中鋼板和預制破片厚度均為2 mm，破片總數為89枚，總質量為34.9 g，采用對稱方式布置（見圖2）。

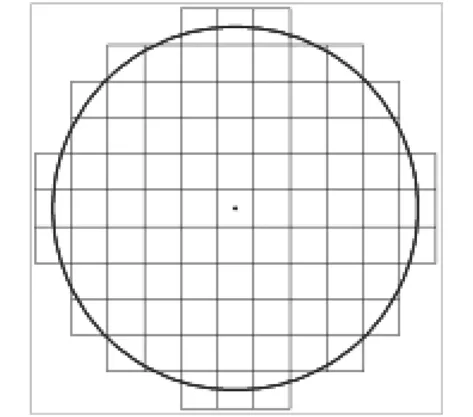
圖2 模型2預制破片布置圖Fig. 2 Placed fragments of model 2

仿真結果如圖3所示，模型1中平板的整體撓曲變形在1 140 μs時趨于穩定，中心最大撓曲變形為39.5 mm，與試驗值42.3 mm相差約為6.62%；模型2中固支方板模型中心處的沖塞破口直徑為56.9 mm，與試驗值相當，其最大撓曲變形出現在破口附近，仿真值為24.4 mm，較試驗值25 mm小約2.4%；模型3和模型4中平板獲得的最終速度仿真結果分別為1 921.6 m/s，1 206.8 m/s，較Gurney平板拋擲公式[19]預測結果1 851.7 m/s，1 246.4 m/s相差分別為3.8%，2.80%。通過以上比較可知，該仿真方法及選取的模型參數較為合理。

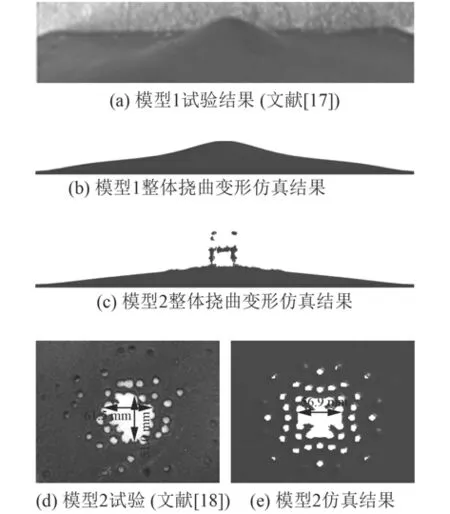
圖3 試驗結果與模型仿真結果Fig. 3 Experimental and numerical simulation images of damaged steel plate

1.3 沖擊波對高速破片繞流作用分析

圖4給出不同時刻下沖擊波的傳播狀態。其中圖4（a） ～ 4（c）為模型2的壓力云圖，從圖中可以清楚看出爆炸前，由于破片群無間隙密集布置，爆轟波遇到預制破片后發生反射（t=30 μs），端部爆炸產生的能量初期主要轉化為破片的動能。由于受到爆炸作用，高壓沖擊波持續作用于破片群后，形成與破片群飛散輪廓一致的凸起高壓區。由于不同位置破片飛散角不同的飛散特性，隨著破片加速運動，破片之間的間隙逐漸增大，在破片群后方沖擊波穿過破片間隙（t=50 μs），并繞流至破片之前，在破片前碰撞形成新的沖擊波向前繼續傳播。同時，炸藥側面爆炸產生的高溫高壓壓縮炸藥側面附近區域的空氣，使空氣的壓力密度迅速上升形成弧形沖擊波向外傳播。近破片端受到破片影響，側面沖擊波向軸向繞流，隨傳播繼續與繞流穿過破片間隙的沖擊波碰撞結合，形成凸形沖擊波，是作用于軸向平板結構的主要沖擊波載荷。

圖4（d）和圖4（e）為模型3的壓力云圖，圖4（f）為模型4的壓力云圖。當一端為拋擲平板時，從圖中可以看到沖擊波對高速破片的繞流主要表現在側面沖擊波繞流至軸向傳播。平板正后方沖擊波強度較高并持續推動平板向前運動，平板邊緣則發生沖擊波的局部渦流運動。模型4中平板質量更大，側面繞流至軸向傳播的沖擊波傳播較平板更加靠前。而且可以看出當炸藥一端為覆蓋整個炸藥端面的平板時且平板在爆炸載荷作用下不發生破碎，沖擊波很難從兩側直接繞流至破片正前方。綜上現象可以看出沖擊波對破片的繞流作用與破片之間間隙、破片尺寸以及破片質量因素存在一定的關系。

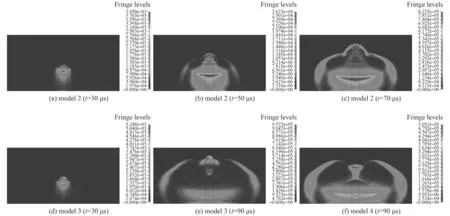
圖4 模型沖擊波壓力云圖Fig. 4 Pressure contours of the model 2/3/4

1.4 計算工況

為進一步分析比較爆炸產生的沖擊波對不同高速破片繞流作用的差異。在同等裝藥工況下，通過變化預制破片間隙d、單一預制方形破片邊長a和破片質量M，進一步研究破片間隙、破片尺寸和破片質量因素對沖擊波繞流作用的影響規律。本文建立了如表4所示計算工況模型進行仿真計算，并在距離炸藥預制破片端150mm爆距水平位置選取測量點。根據文獻[17]可知在150 mm近爆工況鋼板的碟形變形區為半徑125 mm的圓形區域，所以取預制破片端距離炸藥150 mm爆距，半徑R=125 mm的圓形區域（見圖5）為測量區域。讀取軸向測點1的峰值超壓ΔPm、比沖量I1及測點1～測點6的比沖量平均值I2，與裸藥空爆工況（case-1）比較，對比分析沖擊波對高速破片的繞流能力及繞流沖擊波的強度。

2 計算結果分析

2.1 破片間隙對沖擊波繞流作用影響

圖6是破片間隙與破片邊長比值d/a分別為0，0.4，0.8三個工況在35 μs時的沖擊波壓力云圖。從圖中可以看出當預制破片在爆炸前不存在間隙時，在破片前傳播的沖擊波主要還是側面繞流至破片正前方的沖擊波。而當預制破片在爆炸前存在間隙時，沖擊波將迅速通過破片間隙繞流至破片之前。由于從破片間隙繞流出去的沖擊波傳播速度較快，很快與側壁繞流的沖擊波碰撞匯合，形成新的沖擊波，在波頭和破片之間存在長錐形的正壓區域，并且隨破片間隙增大，軸向沖擊波波形更加接近于裸藥空爆的波形。

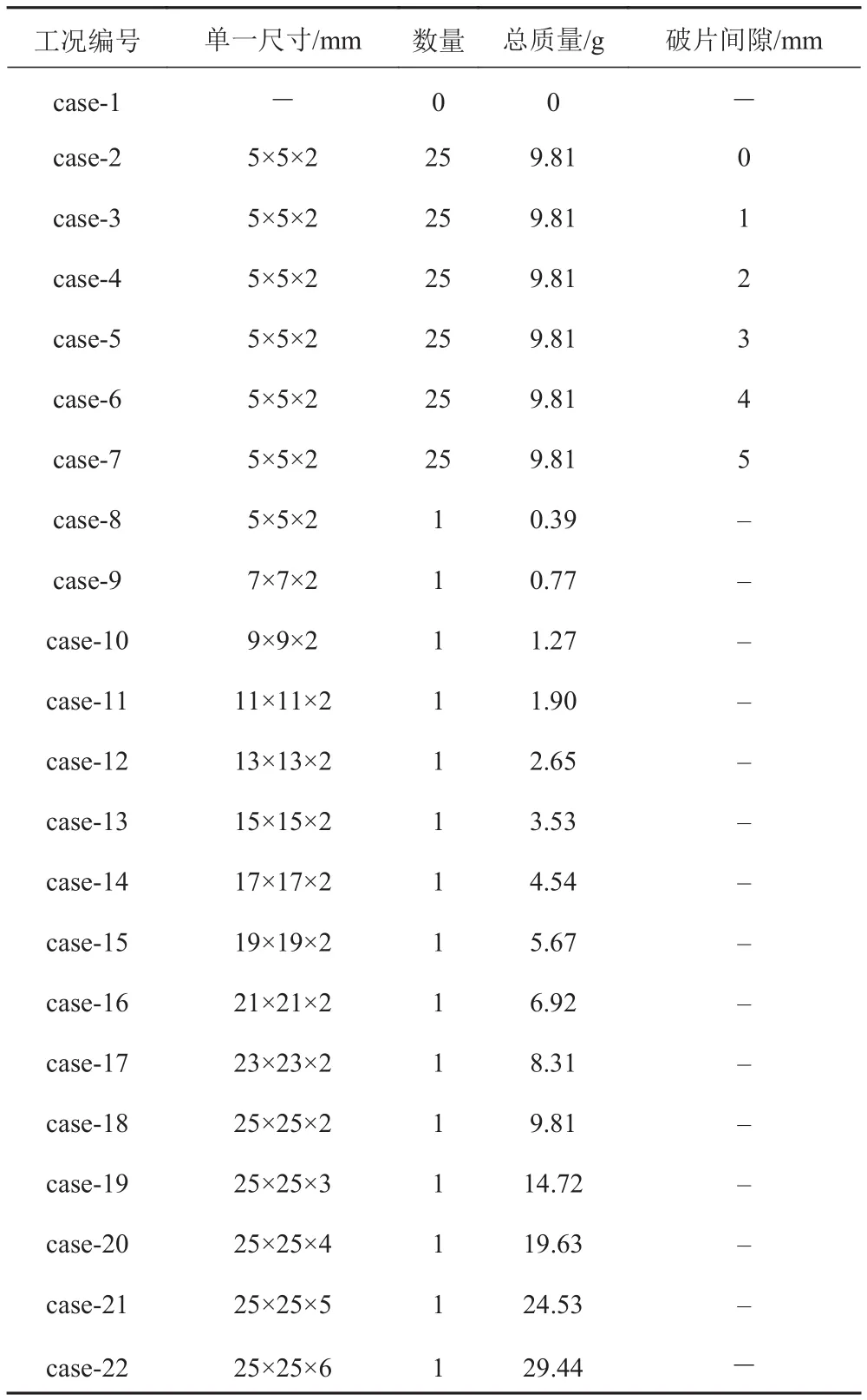
表4 計算工況Tab. 4 Computational conditions

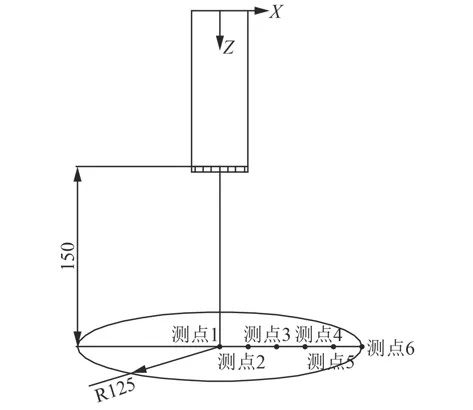
圖5 觀測點分布Fig. 5 View point

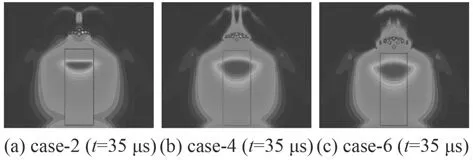
圖6 模型case-2/4/6在35 μs時沖擊波壓力云圖Fig. 6 Pressure contours of the case-2/4/6 at 35 μs

圖7為不同間隙工況下測量區域的沖擊波超壓和比沖量變化折線圖。圖中ΔPm0，I10，I20分別為裸藥空爆仿真模型（case-1）中，測點1的超壓值、測點1的比沖量以及測點1 ～ 測點6的平均比沖量，后文與此相同。分析圖中折線可以看出，無間隙時，沖擊波超壓及比沖量比b/a=0.2工況均要大，這主要是因為此時繞流至破片之前的沖擊波主要由破片兩側邊緣的沖擊波繞流至破片之前碰撞生成，而且碰撞后軸線附近沖擊波存在疊加增強作用。有間隙時，隨著破片間隙的增大，爆距15 cm處的沖擊波超壓和比沖量均呈增大趨勢，但破片間隙達到0.6倍破片邊長后，破片間隙對繞流沖擊波強度影響減小，而且隨破片間隙增大測點處沖擊波超壓和比沖量數值逐漸逼近裸藥空爆沖擊波的超壓和比沖量。

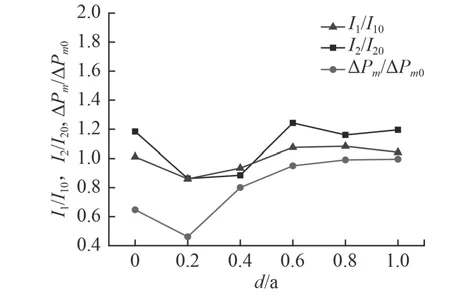
圖7 破片間隙對沖擊波繞流影響Fig. 7 Influence of fragment clearance on wave turbulent flow

2.2 破片尺寸對沖擊波繞流作用影響

圖8是邊長分別為5 mm，15 mm，25 mm，厚度為2 mm的單枚預制破片工況在26 μs時的沖擊波壓力云圖。從圖中可以看出沖擊波對小尺寸破片的繞流能力要比對大尺寸破片的擾流能力強得多，隨著破片尺寸增大，破片對TNT炸藥端部的覆蓋率增大，破片兩側邊緣的沖擊波繞流速度明顯減慢。

圖8 模型case-8/13/18在26 μs時沖擊波壓力云圖Fig. 8 Pressure contours of the case-8/13/18 at 26 μs

圖9為不同破片尺寸工況下測量區域的沖擊波超壓和比沖量變化折線圖，其中R為炸藥半徑。從圖中可以分析得出，隨破片尺寸增大則迎爆面面積逐漸增大，繞流形成的沖擊波強度逐漸減小；繞流沖擊波超壓值低于裸藥空爆沖擊波超壓，但測量區域繞流沖擊波的比沖量要明顯高于裸藥空爆沖擊波。

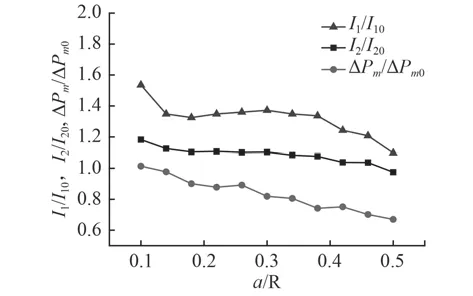
圖9 破片尺寸對沖擊波繞流影響Fig. 9 Influence of fragment size on wave turbulent flow

2.3 破片質量對沖擊波繞流作用影響

圖10為邊長25 mm厚度分別為2 mm，4 mm，6 mm的單枚預制破片工況在50 μs時的沖擊波壓力云圖。從圖中可以看到此時沖擊波主要為兩側繞流沖擊波碰撞產生，并在對稱軸線上生成碰撞增強的高壓點。當破片迎爆面面積不變時，隨破片質量增加，繞流形成的沖擊波波形差異不大，但破片質量越大，其加速越慢，沖擊波繞流過破片并與破片分離速度更快。

圖10 模型case-18/21/23在50 μs時沖擊波壓力云圖Fig. 10 Pressure contours of the case-18/21/23 at 50 μs

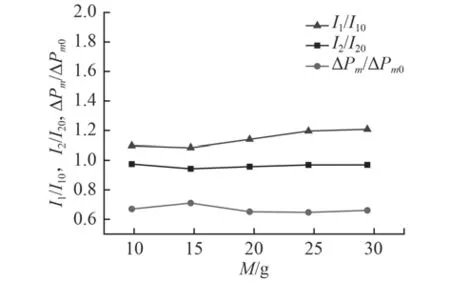
圖11 破片質量對沖擊波繞流影響Fig. 11 Influence of fragment mass on wave turbulent flow

圖11為不同破片質量工況下測量區域的沖擊波超壓和比沖量變化折線圖。從圖中可以分析得出，隨破片質量增大，通過圓形測量區域的沖擊波比沖量強度整體變化不大，測點1的超壓始終低于ΔPm0，但測量點1的比沖量呈增大趨勢。破片質量的增加，主要會增強軸線上沖擊波的比沖量。

3 結 語

本文利用有限元分析軟件Ansys/LS-DYNA計算了實驗模型、Gurney平板拋擲模型，驗證了仿真模型的可行性。通過對比分析仿真模型，研究了破片間隙，破片尺寸和破片質量等因素對沖擊波繞流的影響規律。得到結論如下：

1）爆炸初期沖擊波速度高于破片速度，在對破片加速的過程中，沖擊波對高速破片存在繞流作用。

2）當預制破片端為破片群時，沖擊波主要透過破片之間間隙，繞流至破片之前碰撞形成新的沖擊波向前傳播；而對于單一大破片，在破片前傳播的沖擊波主要是從破片兩側邊緣繞流的沖擊波在軸線附近碰撞產生，碰撞后對軸線上的沖擊波有一定的加強。

3）當預制破片間存在間隙時，隨破片間隙的增大，軸線方向的沖擊波超壓和比沖量增大，其波形和強度都越來越近似于裸藥空爆的沖擊波。

4）單一預制破片尺寸越大，沖擊波對破片的繞流能力越差，繞流產生的沖擊波強度隨破片尺寸增大而逐漸降低。

5）迎爆面積不變，變化單一預制破片質量對繞流沖擊波的波形及強度影響不大，但隨破片質量增加，沖擊波繞流過破片速度加快。